纵-扭耦合下钻柱粘滑振动特性研究

田家林，刘亚迪，熊洁

（西南石油大学 机电工程学院，成都 610500）

随着钻柱长度增加，钻柱系统刚度减小，形成柔性转子系统，导致屈曲，粘滑和其它影响钻井正常工作的钻柱振动现象，是增加钻井成本、延长钻井周期的主要原因[1-3]。钻井深度增加时钻柱环境恶劣程度增加，岩石特性发生改变，增大了钻柱运动的复杂性[4]。钻柱与井壁，钻头与地层岩石界面的冲击和碰撞以及各种振动模式之间的能量交换同时耦合在一起，具有相当复杂的性质，其中以粘滑振动的影响最甚。为了降低成本，防止钻柱疲劳失效，提高钻井速度，必须采取各种措施，提高钻井效率和安全[5-6]。

周银锋等基于旋转体和悬臂梁系统，在稳定的转盘转速下研究钻柱扭转振动问题，根据Lagrange方程，利用系统动能守恒原理，推导出了系统的运动微分方程[7]。张晓东等分析了钻头-岩石的切削模型，建立了其相互作用的摩擦模型，通过对粘滑振动的稳定性进行分析，得到边界稳定状态的临界钻压[8]。Patil 和Teodoriu 在不考虑钻头横向振动的前提下，对垂直井眼中钻柱的粘滑振动现象进行研究，建立了二自由度扭转摆模型[9]。Kong 等提出了一种传感器位置优化算法，建立并实现了能够实时抑制深孔钻具中的模态振动的系统[10]。Viguié等用相平面法研究了钻柱系统中粘滑振动频率、转速以及粘滞系数对钻井振动的影响[11]。Liu 等考虑了钻头时滞及多重再生效应，并建立了钻柱离散模型研究了钻柱系统的非线性运动[12]。Leine 等基于简单的单自由度的旋转力学模型，分析了在不同转速下钻头粘滑振动的分岔图，揭示了不连续的分岔现象[13]。唐昕等探讨了二自由度自激振荡系统中阻尼对粘滑运动的影响，对摩擦不连续性采取光滑连续处理，得出了阻尼对自激振荡系统运动状态和粘滑行为的作用规律[14]。李子丰等通过简化旋转钻井系统对钻柱纵向和扭转振动状态和产生原因进行了分析[15]。Liu等通过建立二自由度扭转模型，研究了1 000 m 钻柱系统的轴向及扭转耦合运动，采用半离散法对钻柱系统的地线性化模型稳定性进行分析[16]。Kapitaniak 等应用ABAQUS 软件建立钻柱有限元模型，对钻柱的弯曲变形和粘滑振动加以分析，并与实验结果进行了比较[17]。

本文考虑纵向激励对钻柱振动的影响以及钻头与岩石之间的非光滑摩擦因素，建立两自由度钻柱纵-扭耦合振动力学模型，仿真分析了纵向振动与扭转振动的动力学特性，对特定参数条件下的钻头处钻压及扭矩进行仿真分析，得到钻柱纵向振动特性、扭转振动特性以及钻头处的钻压及扭矩，研究了不同参数对耦合力学模型下的粘滑振动的影响。

1 纵-扭耦合振动模型

地层与钻头接触产生的粘滑振动，会激励钻柱发生严重的扭转和纵向振动，为描述与这两种振动模式相关的非光滑现象，建立纵向与扭转振动耦合的数学模型如图1 所示。

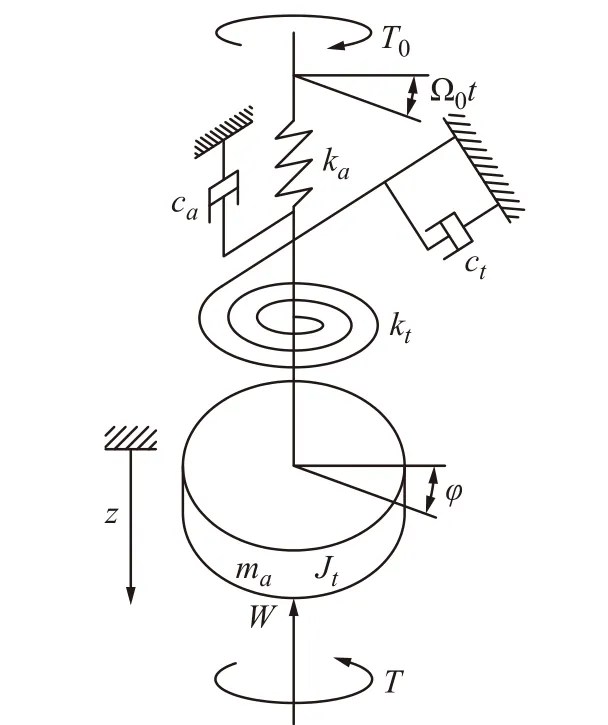
图1 钻柱系统纵-扭耦合简化模型

对模型提出以下假设：研究的钻柱系统处于垂直井中，钻柱的轴线与井筒的轴线保持一致；钻台上部静钻压与钻台转速恒定分别为W0、Ω0；钻柱不与井壁接触且不发生横向振动。采用集总参数法，将井底钻具组合（BHA）视为钻柱底部的集总质量，将钻杆质量视为与其分布质量相等的集中质量，钻具组合质量与等效钻杆质量共同构成轴向质量ma，T0为钻柱系统的输入扭矩，T(φ，z）为钻头处摩擦扭矩，其大小与钻速和纵向激振力有关。

钻头与岩石刚接触时，接触点为坐标轴的原点，即z=0，当钻头向下运动时，z变量为正。若此时钻头在轴向方向上的位移为z0，根据钻柱受力情况，由牛顿第二定理可得，在轴向方向有

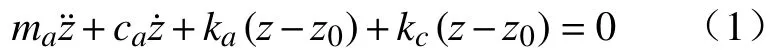
式中：ca为钻柱轴向阻尼；kc为地层刚度；ka为钻柱轴向刚度；kcz为地层对钻头施加的轴向力，方向总是沿轴线方向向上且为正。进行移项化简后，地层与钻头间的作用力用钻压表示为

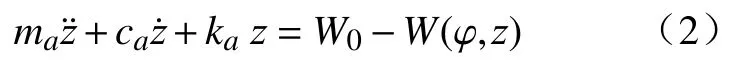
式中：W0为BHA 提供的纵向压力；W(φ,z)为钻头所受的纵向力，与轴向位移z有关。由于轴向力是轴扭耦合的结果，并且这种耦合建模考虑的因素较多，引入扭转模式，即

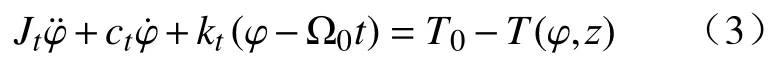
选取x为系统的状态矢量，定义为

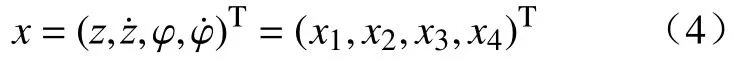
钻柱系统动力学方程可用1 阶微分方程组表示为：

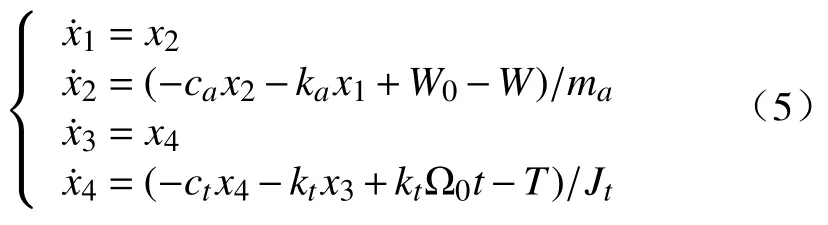
将上式写成状态空间方程形式，即

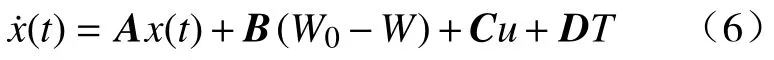
式中：u=T0为控制扭矩；A、B、C、D均为状态空间方程参数矩阵。

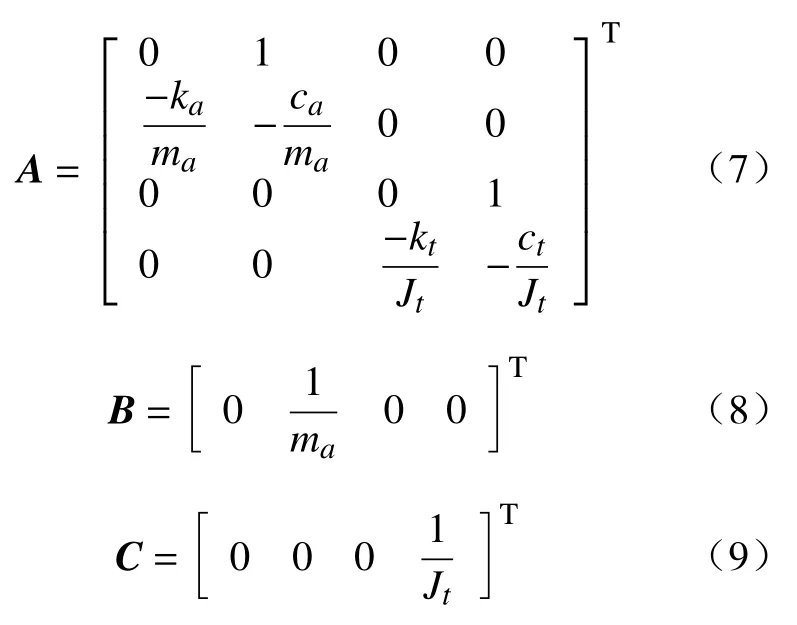
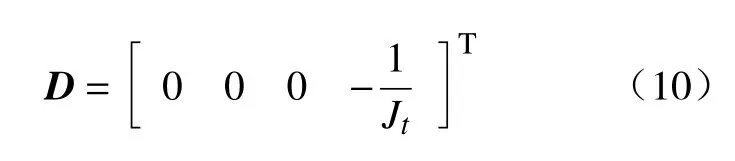
2 边界条件与接触界面建模

钻头开始切削破岩时，岩石与钻头之间的干摩擦会使系统在扭转振动模式下变得不光滑，作用在钻头上的扭矩包括两种形式：与钻头和岩石所用的摩擦特性有关；与切割岩石所需的破岩扭矩有关。假设钻头正面的摩擦力分布均匀，则该扭矩表示为

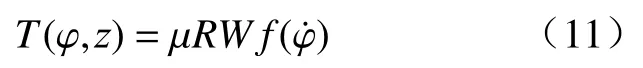
式中：μ为摩擦因数；R为钻头半径；f()为既可以定义静摩擦又能描述动态摩擦的连续函数。

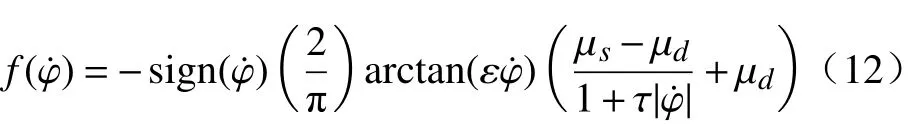
式中：常量 µε和µd分别为静态和动态摩擦因数；ε和τ为无量纲数值常量。在钻柱系统的非线性振动中，这些常数如果选择恰当，将使干摩擦的平滑形状真正接近于原来的非光滑函数，通常ε≪1，τ＞0，其物理意义表示转速对扭矩的影响。在分析钻柱系统纵向与扭转耦合振动的模型中，s0为其振幅，定义切削深度s为

钻头与岩石的相互作用可分为以下4 种形式：

1)切削模式

当钻头开始钻进时，钻头的角速度 φ开始逐渐增大，切削深度s也随钻头的钻进而增大，钻头正常钻进，钻头与岩石之间的作用力表示为

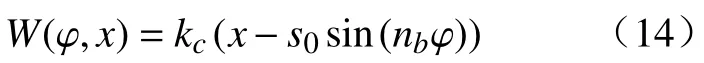
2)粘滞模式

当钻头与岩石作用的摩擦力逐渐增大时，钻头处的切削扭矩小于摩擦扭矩，钻头将静止不动，产生粘滞现象，此时钻头处的角速度 φ为0，且钻柱系统处于“憋矩”的状态。

3)滑脱模式

当钻头处的扭矩积蓄到足以克服岩石的摩擦扭矩运动时，钻头处的角速度φ ＞0，并且将可能超越转盘的转速 Ω0，此时钻头不再切削岩石，切削深度s=0。

4)跳钻模式

当钻头与岩石在没有接触的情况下，即x＜s0sin(nbφ)时，切削深度s＜0，钻头与岩石不接触，钻头与岩石所产生的纵向力为0，钻头与岩石处的扭矩0，此时钻头处于跳钻模式，钻柱轴向与扭转振动的刚度分别为：

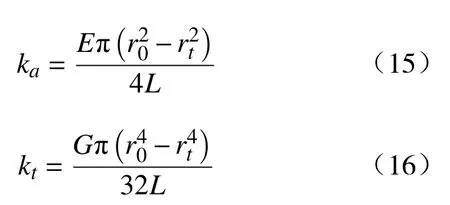
扭转阻尼为

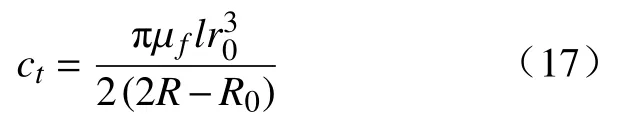
扭转惯量为钻具的组合惯量和等效钻杆惯量之和，即

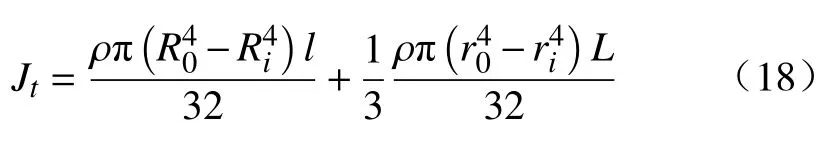
3 算例分析

基于龙格库塔法以及自适应步长法对以上所建立的模型进行求解，利用MATLAB 软件进行编程和数据处理，模拟仿真的算例参数如表1 所示。

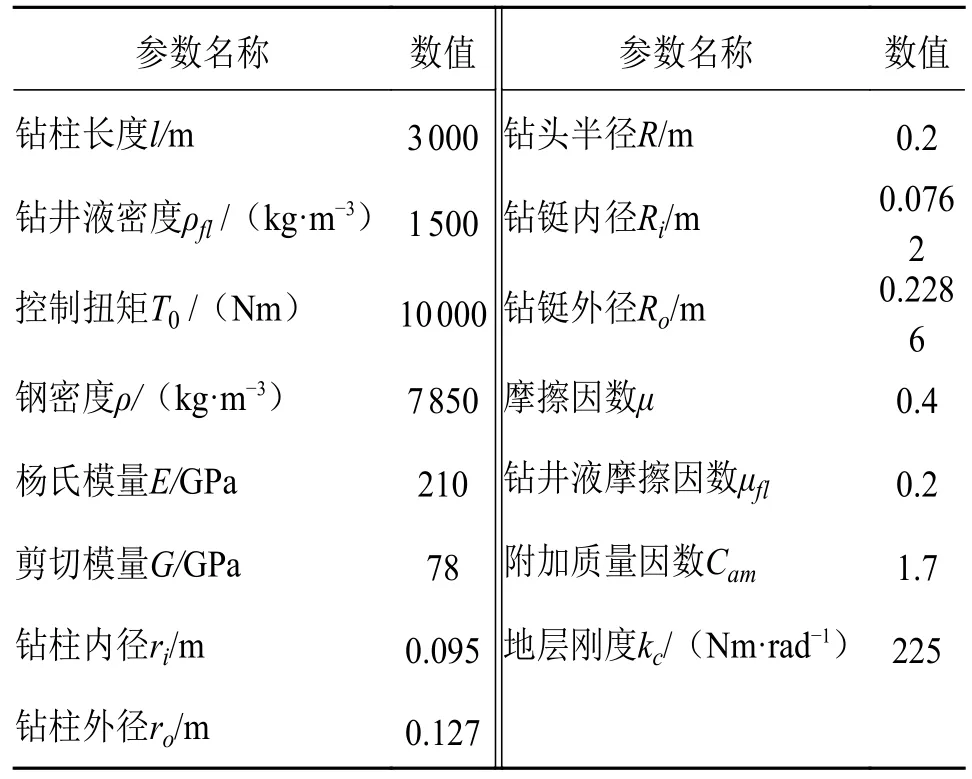
表1 算例基本参数

钻柱纵-扭耦合的振动特性仿真结果见图2。由图2a）可知，钻头轴向振动位移稳定在-0.015～-0.02 m 区间范围内；由图2b）可知，钻头进给的速度并不恒定，其峰值为0.5 m/s；由图2c）可知，钻头处的轴向位移主要集中于0.01～ 0.02 区间以及-0.015～-0.05 区间内，钻头处的轴向振动速度主要集中于0.03～ 0.05 以及-0.03～-0.05 区间内，钻头轴向振动为正表明钻柱系统正常钻进，机械转速正常，轴向振动为负表明钻头处与岩石脱离，并向上跳动，有跳钻危险；由图2d）可知，钻头处所受的钻压并不稳定，其峰值为5×105左右，且有钻压为零的现象存在，这是由于钻头处于粘滞阶段时钻柱扭曲，而在滑移阶段时，钻头与岩石脱离，从而产生跳钻，导致钻杆因疲劳断裂失效。

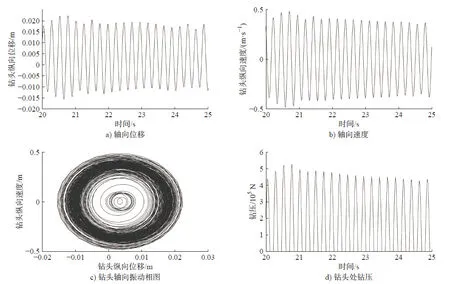
图2 钻柱系统纵-扭耦合轴向振动动力学特性

钻柱系统纵-扭耦合扭转振动动力学特性见图3。由图3a）可知，钻头产生明显的粘滑振动现象，振动频率为0.22 Hz 左右，钻头角速度峰值为25 rad/s，达到转盘转速的2 倍，此时钻头处于粘滞阶段，钻头处的角速度为零，但转盘依旧在匀速转动，钻头所受的扭矩逐渐增大，由图3b）可知，钻头与转盘处的相对角位移处于-10 rad～ +15 rad 区间之内，相对角位移为正时，表明钻头超前于转盘，相对角位移为负时，表明钻头滞后于转盘；由图3c）可知，钻头处扭转相位图为极限环状态，且出现明显抖颤，钻头处的扭矩峰值可达3.5×104Nm，钻压和扭矩存在为零的情况，由图3d）可知，钻头处不断储存能量，当驱动扭矩逐渐大于摩擦扭矩时，能量瞬间释放，钻头转速达到峰值，产生十分严重的扭转振动，由于轴向振动的影响，钻头角速度数值有抖颤。

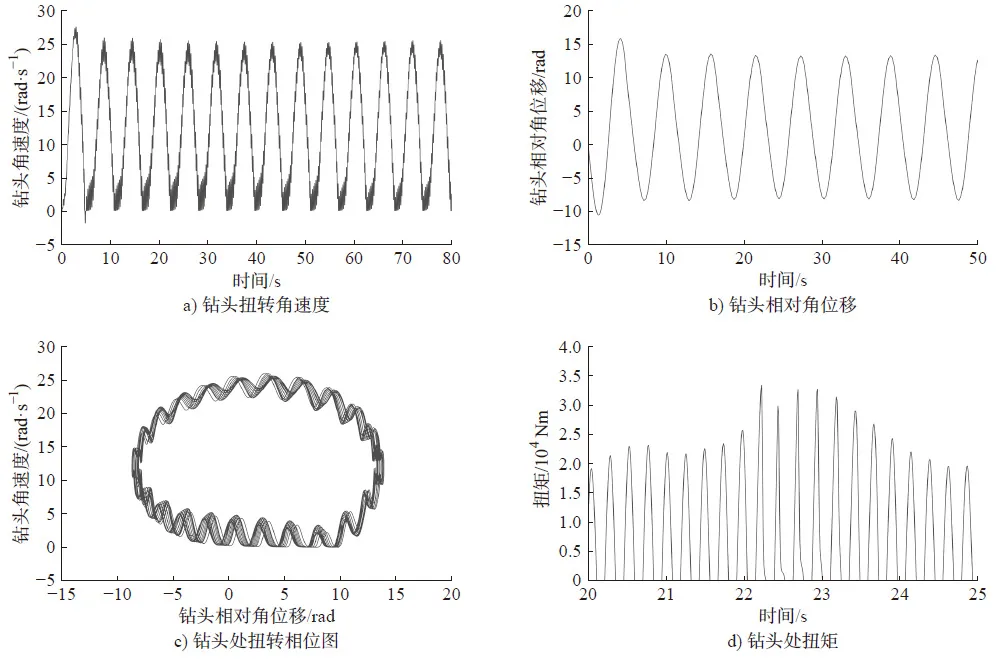
图3 钻柱系统纵-扭耦合扭转振动动力学特性

图4 为钻柱系统在顶驱转速为110 r/min 时钻柱振动速度信号频谱图。可以看出未考虑横向振动影响的钻柱纵-扭耦合振动是以一阶固有频率为基频成份，只在基频处出现尖峰，此时钻柱做周期运动；纵向速度频率高于扭转速度的频率，表明纵向振动是高频振动，但其幅值更低；在驱动转速处频率处无明显幅值分量，表明系统振动并非是由旋转运动而产生的受迫振动，而是由系统的非线性因素引起的自激振动。

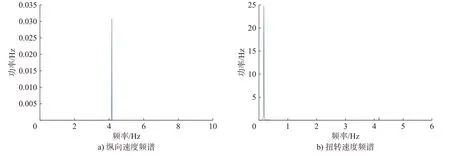
图4 钻柱振动速度信号频谱图

从图5 可以看出，在一定初始时间内，钻头受到扭矩小于钻头破岩所需最小扭矩，此刻钻柱发生粘滞运动，钻头转速为0，钻柱产生扭转变形，直到变形产生的扭矩大于钻头破岩所需最小扭矩；当粘滞运动结束后，钻头开始进行滑脱运动，初始时刻钻柱因变形产生扭矩大于钻头受到动摩擦扭矩，钻头转速逐渐增加；当钻头受到的动摩擦扭矩大于钻柱变形产生的扭矩时，钻头转速逐渐减小为0。从图6可知，钻头处的相对角位移代表了钻头处的角位移与转盘速度与时间乘积的差值，增大转盘的转速时，钻头的相对角位移幅度逐渐减小，说明钻头与转盘运动同步性逐渐增大，钻头的粘滞时间减少，明显降低了粘滑现象。

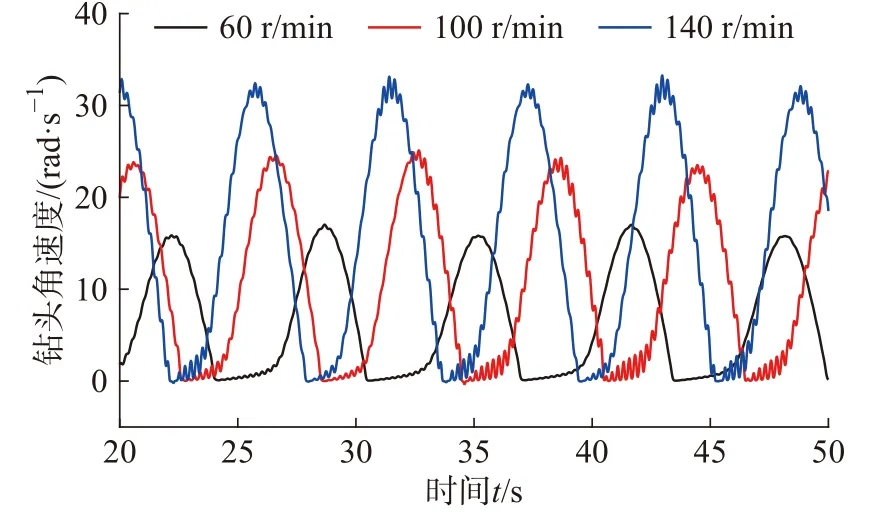
图5 不同转速下钻头扭转角速度时域图

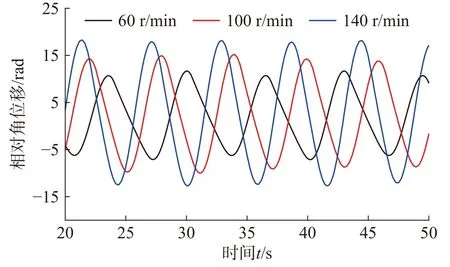
图6 不同转速下钻头扭转相对角位移时域图

图7 和图8 分别为调节不同的钻压，得到的钻头角速度与相对角位移情况。当钻压不断增大时，钻头粘滞时间变长，钻头角速度幅值变化为转盘转速的2 倍左右，选择较小的钻压时，钻头角速度抖颤越小，粘滞时间变短，当钻压低于临界值时，钻头处将不再出现粘滑振动现象。增大钻压会使钻头角速度逐渐减小，导致钻柱加重粘滑现象，当钻压增大到一定值后会增大岩石与钻头处的摩擦力，使钻头钻进困难，若持续增加则会导致卡钻的风险。

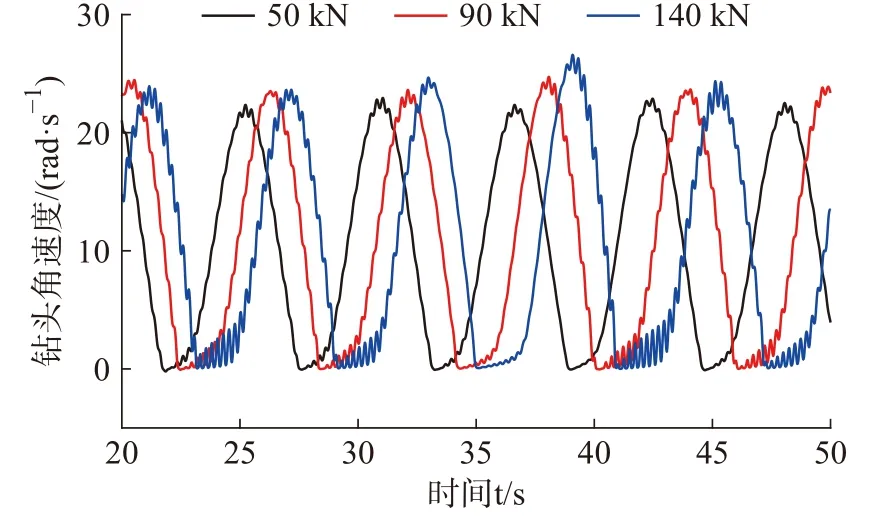
图7 不同钻压下钻头扭转角速度时域图

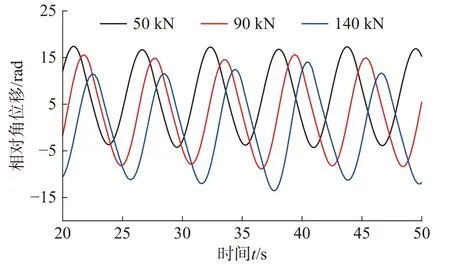
图8 不同钻压下钻头扭转相对角位移时域图

4 结论

1）特定参数下的钻柱纵向及扭转振动特性进行仿真分析，得到钻压及扭矩的变化情况。结果显示钻压和扭矩并不稳定，在钻头粘滞时期，钻压及扭矩变化较大。

2）对纵向速度和扭转速度进行分析，结果表明钻柱纵-扭耦合振动是以一阶固有频率为基频成份，且只在基频处出现尖峰，纵向速度频率高于扭转速度的频率，表明纵向振动是高频振动，但其幅值更低；在驱动转速处频率处无明显幅值分量，表明系统振动并非是由旋转运动而产生的受迫振动，而是由系统的非线性因素引起的自激振动。

3）对不同钻井条件下的扭转振动及纵向振动特性进行仿真分析，可知在高转速、低钻压的钻井条件下，钻柱系统粘滑振动现象减弱。