基于突变理论的岩溶隧道填充物溶腔底板失稳数值分析

张军， 刘远

(1.长沙理工大学 土木工程学院， 湖南 长沙 410114；2.贵州省宏信创达工程检测咨询有限公司， 贵州 贵阳 550014)

1 引言

中国的交通行业高速发展，尤其是在西南地区修建隧道过程中遇到的各种问题越来越严重，例如在喀斯特地区修建隧道时，经常伴随着塌方、突水涌泥的地质灾害，一方面制约工程的发展[1-4]；另一方面危害到人身安全。岩溶隧道开挖过程中会遇到填充型溶腔、承压水溶腔和竖向溶槽等不良地质，溶腔内的填充物对周边岩层产生一定的冲击和侵蚀，岩层不足以承担上部荷载的冲击造成失稳破坏[5]，因此对岩溶隧道突水涌泥机制等问题的研究对工程应用具有很大价值。该文以湖南永吉高速公路六月田隧道顶部涌泥为例进行分析研究。

2 填充物溶腔底板失稳因素分析

六月田隧道的填充型溶腔位于隧道顶部，并且溶腔尺寸大于隧道的轮廓，根据突变理论尖点突变模型，简化填充型溶腔底板为周边固支的圆形板，半径为r0，底板厚度为t，ω为填充型溶腔底板挠度，填充型溶腔底板岩层的弹性模量为E，泊松比为μ。岩层自重q和填充物的作用力p作用在底板岩层上(图1)。

图1圆形板力学模型的边界条件为[6-8]：

(1)

式中:ur为径向位移；ω=(fr)。

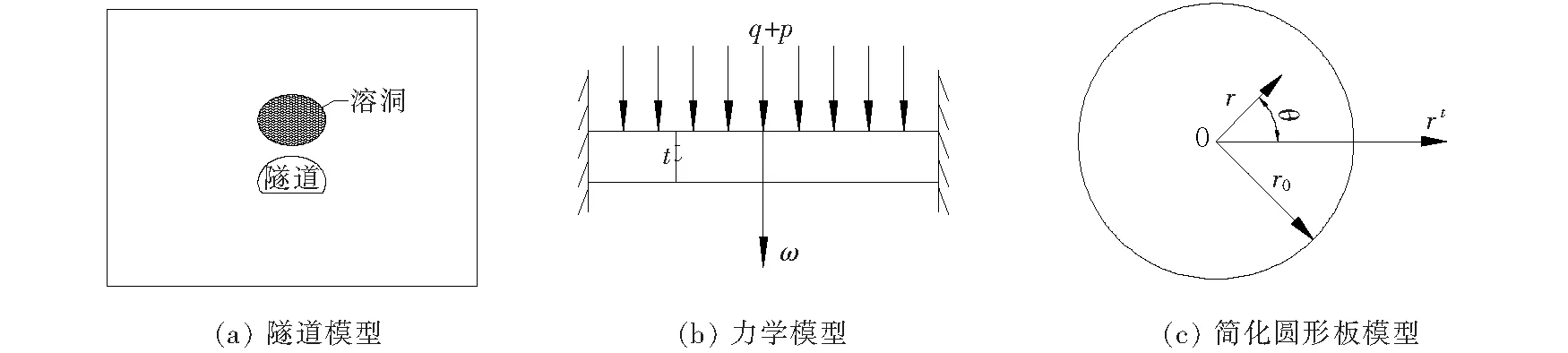
图1 简化圆形板力学模型

根据相关文献已知板的弹性理论，圆形板弯曲变形的表达式为:

(2)

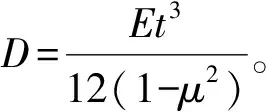
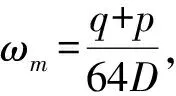
(3)

按照边界条件式(1)，径向位移ur级数表达式如下:

(4)

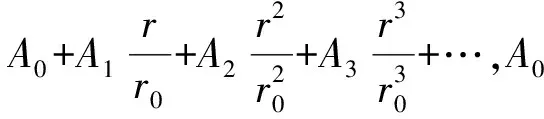
(5)

由弹性力学的变分法可求得：

(6)

式中：b1、b2为常数。

将式(6)代入式(5)，得到：

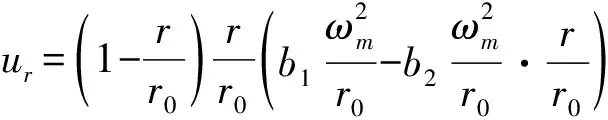
(7)

填充溶腔底板岩层系统的总势能函数表示如下:

Π=U-W

(8)

式中：U为岩层内部的变形势能；W为外力所做的功。

根据弹性力学理论，U1为底板岩层的弯曲变形势能，U2为底板岩层相应于中面应变的势能，因此U可表达为：

U=U1+U2

(9)

(10)

(11)

对式(10)、(11)进行积分可求得：

(12)

把式(12)代入式(9)可求得岩层内部总势能：

(13)

式中:b3为常数。

岩层自重及岩层上方覆盖层q和填充物p所做的功为W1；岩层自重和填充物在径向位移方向上所做的功为W2，两者之和即为总功，表达为：

W=W1+W2

(14)

W1=∬(q+p)ωrdθdr,W2=∬(q+p)urrdθdω

(15)

对式(15)进行积分可求得：

(16)

将式(16)代入式(14),可得外力所做的功为：

(17)

式中:b4为常数。

将式(13)和式(17)代入式(8)，可得填充溶腔底板岩层系统的总势能函数表达式为:

(18)

假设：

(19)

根据式(19)可将式(18)简化为：

(20)

根据Tschimhaus变换，令：

(21)

另外设：

(22)

通过式(21)、(22)可将式(20)简化为：

Π=g4x4+g2x2+g1x+g0

(23)

对式(23)进一步的化简，可令：

(24)

则式(23)可以化简成：

(25)

式中：x为状态参数；u、v为控制参数。

根据突变理论，式(25)可以转换成突变的标准函数：

(26)

(27)

上述公式给出了填充腔体底部岩层结构曲面的稳定性平衡是由状态参数x、控制参数u和v组成的三叶折叠曲面，由上叶、中叶和下叶组成，如图2(a)所示[10-12]。从图2(a)中可以看出；充填溶腔的底板岩层系统在平衡曲面上叶或下叶时是处于稳定状态，因为岩层系统在上叶或者下叶时为极小点；当岩层系统位于中叶时，它是不稳定的，因为此时表现为极大点。引导岩层系统稳定平衡面x、v通过平面投影得到图2(b)。当控制参数v在上叶H到H′移动过程中，溶腔底板仍处于稳定状态，稳定性没有发生本质变化，但是岩层会继续产生蠕变或移动。当控制参数v到A点移动时，岩层系统在极大点的上边界，此时处于临界状态。外部的任何扰动都会使得临界状态向不稳定状态发展，即由图2(a)的上叶突跳至中叶，此时系统是不稳定的，但是系统不会一直停留在此阶段，它会跳跃至下叶，岩层底板经过不稳定阶段后造成失稳破坏。控制参数v由下叶到上叶的移动过程中，必然经过另外一个临界点A，同样不会在中叶停留，会跳跃至上叶。将岩层系统稳定平衡面投影到u、v曲线上可得图2(c)。

图2 尖点突变模型

(28)

根据式(27)和(28)可得分叉集方程：

4u3+27v2=0

(29)

从图2(c)可以看出：只有u≤0，系统才有可能通过分叉集。因此，底部岩层系统不稳定的必要条件为:

u≤0

(30)

将式(19)～(24)代入式(30)可得：

(31)

对式(31)进一步化简可以得到岩层的临界厚度：

(32)

由式(31)、(32)可以看出：导致底板岩层不稳定的因素有:岩层厚度、岩层的弹性模量、岩层上方q+p荷载作用和溶洞的跨度。在必要的失稳条件下，底板岩层厚度越薄，岩石弹性模量越小，溶洞洞径越大，岩层上方荷载作用力越大，底板岩层越不稳定。

3 数值模拟

针对上节力学模型推导所得出的结论，对不同围岩级别的岩溶隧道进行三维数值建模，对于每个计算参数主要指工程地质数据，对于未知参数则可参考JTG 3370.1—2018《公路隧道设计规范》和《工程地质规范》(第四版)，填充参数以试验数据为基础，各参数的具体取值见表1[13]。

为便于分析，径跨比D是由溶洞洞径r和隧道距溶洞之间岩层的厚度t的比值定义的。在开挖三维隧道时，主要研究不同围岩级别的其他影响因素下溶洞填充物对其下部岩层的影响，如表2所示，计算三维隧道的发展模式。

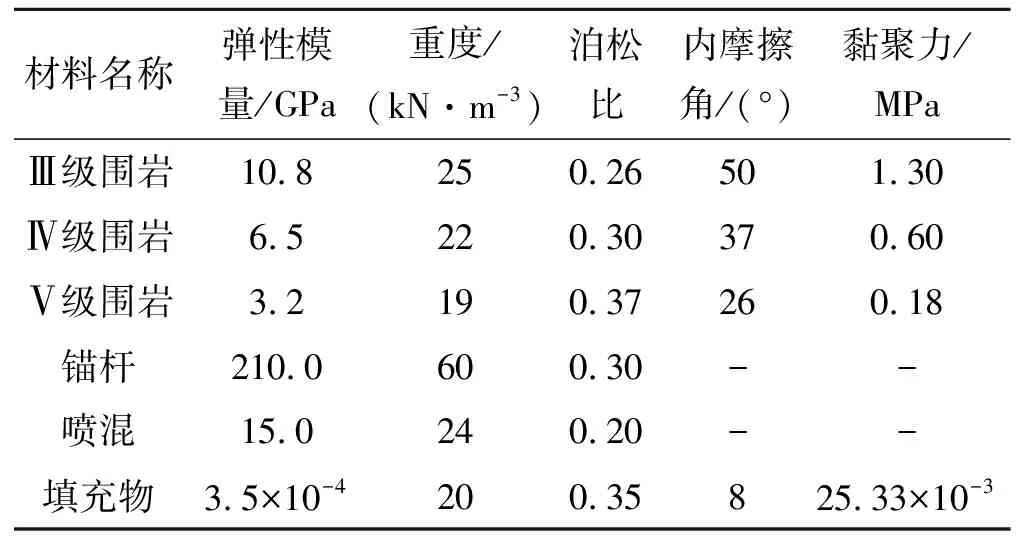
表1 力学参数

表2 三维隧道开挖工况

3.1 垂直位移分析

图3为溶腔底部沉降随隧道开挖推进距离的变化。

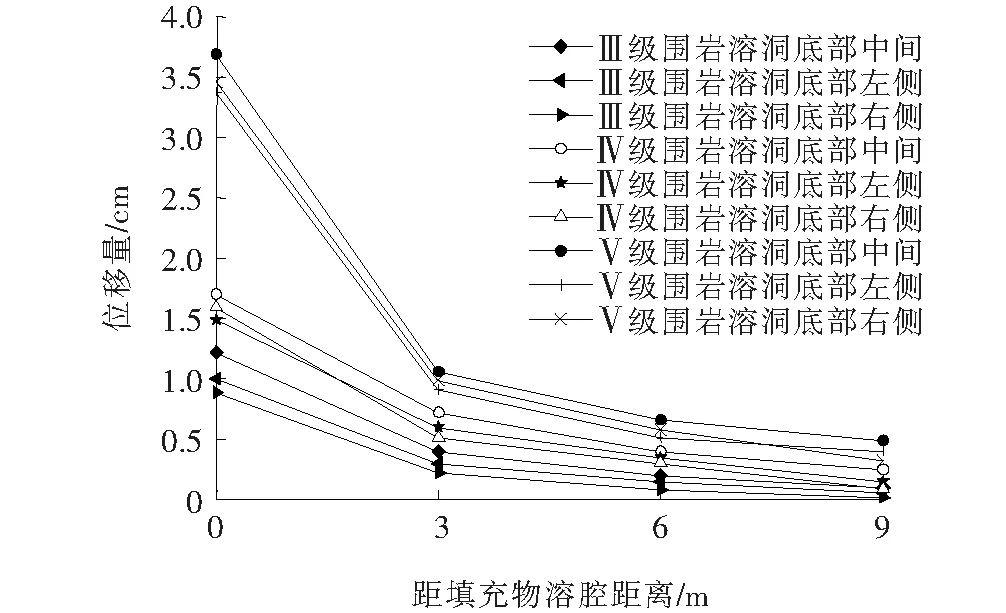
图3 填充物溶腔底部各点沉降随隧道的开挖推进距离的变化曲线

从图3可以看出:随着围岩等级的增加，岩层底板的垂直位移都有所增加[14]，各级围岩岩层底板位移增加幅度的大小关系为：Ⅲ级围岩<Ⅳ级围岩<Ⅴ级围岩，并且各级围岩溶洞底板中间位移的增加量均大于两侧的增加量。综上所述，围岩等级越高，底板岩层越容易失稳破坏，并且底板岩层中间的位移量最大，受到的影响也最大，岩层破坏很有可能发生在中间部位。

3.2 应力分析

图4、5为填充物溶洞底部各点应力随隧道开挖推进距离的变化。

从图4、5来看：隧道开挖前，两侧的主应力值大于中间点。隧道开挖后，中点主应力值大于两侧主应力值。一方面，当隧道开挖到洞的正下方时，充填洞底部岩层中部的主应力变化很大；另一方面，隧道开挖时，无论周围围岩的等级如何变化，底板岩层的应力主要为压应力，主要集中在底板岩层的中间。主应力变化幅度的大小关系为：Ⅲ级围岩<Ⅳ级围岩<Ⅴ级围岩，并且都是底板岩层的中间处受到的影响最大，由此可见，围岩等级越高，溶腔底板岩层的中间部位受到的影响越大，岩层越容易失稳，从而发生地质灾害。

图4 填充溶洞底部各点最大主应力随隧道开挖推进距离的变化曲线

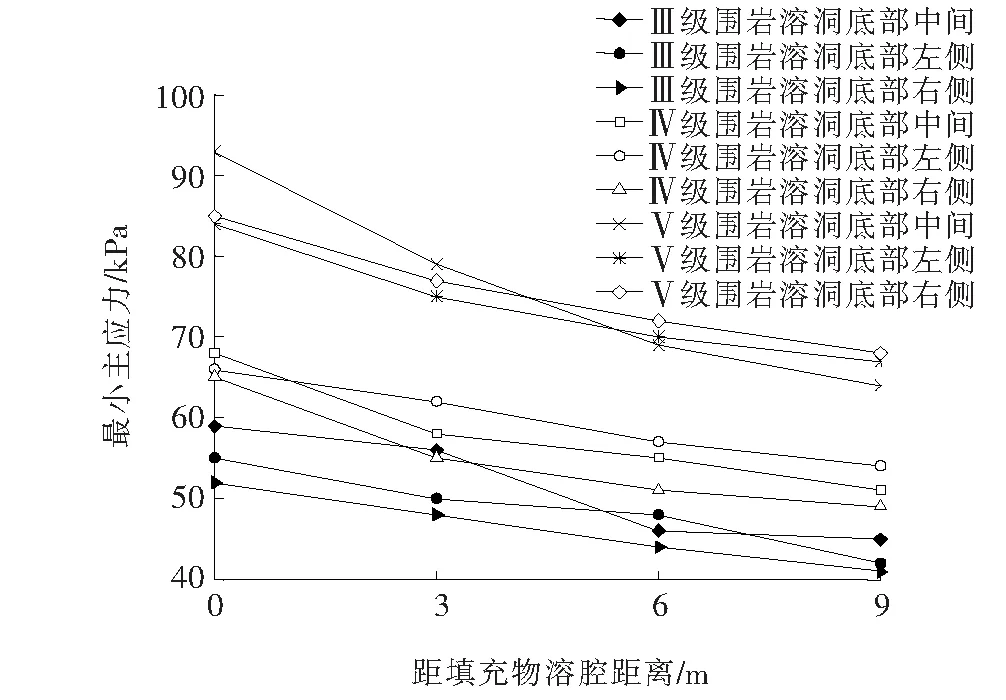
图5 填充物溶腔底部各点最小主应力随隧道的开挖推进距离的变化曲线

3.3 塑性区分析

随着隧道的不断开挖，填充物对不同围岩隧道溶洞底部岩层塑性区的分布影响如图6所示(以距溶腔0 m处为例)。

由图6可以看出：各级围岩底板岩层塑性区范围扩展的大小关系为：Ⅲ级围岩<Ⅳ级围岩<Ⅴ级围岩，底板岩层塑性区分布范围随着围岩等级的增加有明显的增大，溶腔底板周围的围岩越差，塑性区扩展的范围越大，当围岩为Ⅳ级时，塑性破坏区处于临界状态，此时岩层未失稳，当围岩为Ⅴ级时，底板岩层的塑性破坏区已经扩展到隧道拱顶上方，并和拱顶上方的塑性破坏区贯通，说明岩层已经失稳，因此引发突泥涌水等地质灾害。总而言之，围岩等级越高，岩石的坚硬程度降低，围岩完整性越差，弹性模量越小，溶腔底板岩层越容易失稳破坏。

图6 不同围岩溶腔底部岩层塑性区分布图

4 结论

结合湖南省永吉高速公路六月田隧道顶部突泥的实际情况，根据突变理论，简化隧道拱顶上方溶腔为圆形板模型，通过理论推导得出影响填充物溶腔底板失稳突变的因素，结合数值模拟的方法对影响因素进行分析，得出以下结论：

(1) 采用突变理论简化隧道上方填充物溶腔为圆形板，建立相应的力学模型，通过理论计算得出岩层层厚、岩石弹性模量、岩层上q和p加载层的作用是影响填充物溶腔底板岩层失稳突变的主要因素。

(2) 不同围岩的溶腔底板岩层通过三维数值模拟得出底板岩层的垂直位移、应力和塑性区的变化情况。当隧道开挖轮廓正好位于溶洞下方时，各级围岩填充溶腔底板岩层各点的位移和应力均有增加，但中间处的位移和应力增加幅度均大于两侧，当围岩等级为Ⅴ级时，底板岩层中间处的塑性破坏区已经贯穿至隧道拱顶上方，而且和隧道拱顶上方的塑性破坏区贯通。因此岩层失稳突变先从中间处开始，引发突泥地质灾害。弹性模量越小，溶腔底板岩层越容易失稳破坏。