基于结构光测量的三维沥青路面纹理研究

李晓宇, 何欢, 胡江碧

(北京工业大学 建筑工程学院， 北京市 100022)

近年来，随着中国公路建设事业的发展，道路安全问题成为制约公路发展的关键因素之一。路面抗滑性能的优劣严重影响道路交通安全，而路面的抗滑性能与路面纹理构造相关性较高[1-2]。基于此，国内外学者做了大量获取路面纹理三维数据、表征路面构造参数及分析纹理构造参数和路面抗滑性能间关系的研究。杨丽霞、李中伟等[3-4]通过对光栅投影三维形貌测量系统的关键技术及精度问题进行研究，初步建立了结构光三维形貌测量系统；蒋超[5]利用三维结构光检测系统获取水泥路面三维构造信息，并通过Matlab软件计算水泥路面宏观构造表征参数；刘林等[6]利用Matlab软件读取沥青路面三维构造信息，计算轮廓算术平均偏差、轮廓均方根偏差和平均构造深度表征路面纹理，并分析轮廓算术平均偏差、轮廓均方根偏差和平均构造深度与仪摆值的相关性；于世海、李伟、王子彬等[7-9]利用激光检测原理计算路面构造深度，结果可靠性较高；桂志敬等[10]总结路面纹理检测方法及回顾路面纹理表征参数；周纯秀等[11]利用激光轮廓仪获取路面纹路数据，计算算术平均偏差、算术平均波长和轮廓偏斜度构造参数表征路面二维纹理，并用于定量评定路面纹理粗糙度；Li 等[12]利用3D成像技术采集三维纹理数据，计算4种类型的纹理参数(振幅、间距、混合和功能参数)，并分析这些纹理参数和路面摩擦系数之间的关系；Ergun等[13]基于试验数据分析，研究了轮廓算术平均偏差、轮廓均方根偏差等纹理表征参数与路面摩擦系数间的关系。

综上所述可见，在获取路面纹理三维数据、表征路面构造参数及分析纹理构造参数和路面抗滑性能间关系等方面，国内外学者都有重要且有益的探索。但在结合实际不同沥青路面，利用成熟且精密的光学技术手段，综合分析各种三维纹理构造参数与实际路面测试值的相关性，并最终得到最能评价沥青路面抗滑性能的构造参数等方面，还有待于加强。由此，该文基于光栅投影的结构光三维测量系统获取了几种常见的沥青路面表面高程数据，再利用Matlab软件重构沥青路面三维数据模型并计算各种沥青路面纹理构造参数，最后分析各构造参数与基于同样样本的前课题组研究[14]的路面摩擦性能间的相关性，得到用于评价不同沥青路面抗滑性能可选用的构造参数。

1 样本与三维重建

1.1 样本选取

结合实际工程应用情况，选取3种常见的沥青混凝土路面类型(AC-13、AC-16、SMA-13)，分别成型3组沥青混凝土路面试件，每组试件3块样本，各样本尺寸为300 mm×300 mm×50 mm(长×宽×高)，如图1所示。样本材料按照相应规范进行检测，其性能经过北京市道路工程质量监督站检测合格。

图1 选取的3种沥青混凝土路面样本

1.2 三维测量与纹理重建

该文采用光栅投影的结构光三维测量技术，获取沥青路面表面高程点信息，其测量示意图如图2所示。测量系统经过标准样品的矫正，测量的精度为0.05 mm。具体过程为：结构光测量仪将正弦平行光栅条纹投影到沥青路面表面，其中光栅条纹随着路面样本纹理高度的变化而改变，测量仪中左右相机镜头获取变形后的平行光栅条纹，再通过软件获取并修正沥青路面表征纹理高程数据的点云文件，最后利用Matlab软件重构沥青路面三维数据模型(图3)。

图2 光栅投影三维测量系统示意图

图3 重建的三维数字纹理图

2 三维纹理模型有效性验证

基于同样的样本试块，课题组的前研究[14]利用了摆式仪检测了不同温度、冰水等条件下沥青混凝土路面的仪摆值(也称为BPN值)，并采用铺砂法测出路面试样的构造深度。在此，利用重建的数字路面三维纹理为基础，可计算出模拟的构造深度，进而可对比模拟构造深度与试验检测值。此外，可计算并对比两种构造深度与试验仪摆值的相关性，从而进一步验证三维数字纹理模型的有效性。其中，AC-13、AC-16、SMA13样本的试验仪摆值，采用干燥状态下的10 ℃的检测值[14]。

平均构造深度(MTD)常用于表征沥青路面三维宏观纹理构造特征，试验中常用铺砂法测得，其计算可参考式(1)[15-16]：

(1)

式中:V为砂的堆积体积；S为铺设的面积。

该文以光栅投影技术提取并重建的数字路面三维纹理为基础，通过Matlab软件编写公式计算出模拟平均构造深度(EMTD)，其计算可参考式(2)[6]：

(2)

式中:zp(xi,yj)为基于基准线的沥青路面分布曲线高程点最大值；z(xi,yj)为基于基准线的沥青路面分布曲线高程点信息；N为纵向采样长度内的轮廓数；M为横向采样长度内的轮廓数。

AC-13、AC-16、SMA-13样本的模拟构造深度与试验检测的构造深度对比如图4所示。

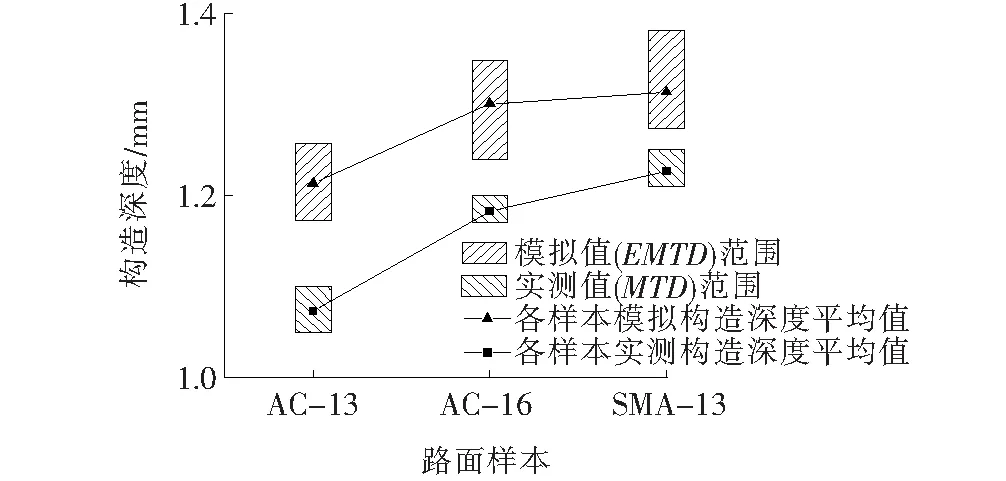
图4 三维平均构造深度模拟值和实测值对比图

由图4可知：3种样本的平均构造深度模拟值与实测值存在相同的数值关系，即SMA-13>AC-16>AC-13，且模拟计算值较实测值偏大0.1 mm左右。其可能原因主要是重构得到的构造深度偏理想，实测中由于砂子的堆积不严实等原因可导致实测数值偏小。类似结论也在基于激光测量研究中发现[8]。由此，初步验证利用上述方法重建的沥青路面三维纹理模型的有效性。

此外，平均构造深度与仪摆值关联性的强弱可利用Pearson相关系数以及Spearman相关系数进行表征，二者计算公式基本相同[6,17]，Pearson相关系数具体表现为：r>0.95或r<-0.95时平均构造深度与仪摆值间显著相关；0.8≤r≤0.95或-0.95≤r≤-0.8时平均构造深度与仪摆值间高度相关；0.5≤r<0.8或-0.80.886或r<-0.886时平均构造深度与仪摆值间显著相关；-0.886≤r≤0.886时平均构造深度与仪摆值间不相关，具体计算可参考式(3)：

(3)

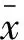
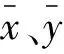
基于3种路面样本的两种平均构造深度(MTD和EMTD)与试验检测仪摆值(BPN)之间的Pearson相关系数及Spearman相关系数，如图5所示。由图5可知:3种样本的平均构造深度实测值和模拟值均与仪摆值之间存在较高的相关性，且SMA-13试件的相关性最高。利用Pearson相关系数与利用Spearman相关系数的评价结果非常相近。 同时，模拟构造深度与试验仪摆值的相关性更显著。由此进一步证明了重建的沥青路面三维数据模型的有效性，其可用于后续研究沥青路面各构造参数与路面抗滑性能的相关性。

3 构造参数与相关性分析

沥青路面的微观纹理和宏观纹理共同影响其抗滑性能。其中，微观构造主要影响车辆低速行驶时沥青路面抗滑性能；宏观构造主要影响车辆高速行驶时沥青路面抗滑性能。因此，该文从高度相关表征参数(平均构造深度、平均断面深度、轮廓算术平均偏差、轮廓

图5 平均构造深度与仪摆值相关性柱图

均方根偏差)、波长相关表征参数(轮廓单峰平均间距、轮廓算术平均波长、轮廓均方根波长)、形状相关表征参数(轮廓算术平均斜率、轮廓均方根斜率)、综合表征参数(偏斜度、陡峭度)4方面选取相关参数评价其与路面抗滑性能的相关性。

3.1 路面纹理构造参数

(1) 平均断面深度(MPD)

平均断面深度用于表征沥青路面二维宏观构造高度相关特性，其计算可参考式(4)：

(4)

式中：h1、h2分别为第一、二分段曲线所有点的高程值的最大值；h为曲线段所有点的高程值的平均值。参数信息如图6所示[15]。

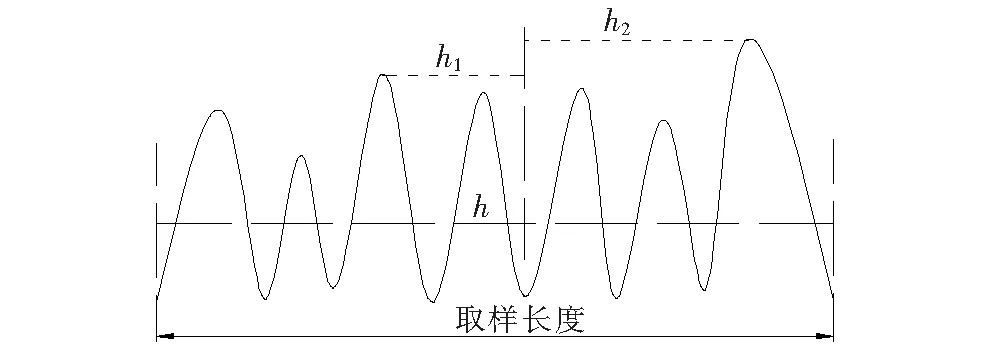
图6 平均断面深度计算参数信息图

(2) 轮廓算术平均偏差Ra和轮廓均方根偏差Rq

轮廓算术平均偏差和轮廓均方根偏差为表征沥青路面纹理粗糙特性的同类型参数，其中轮廓算术平均偏差反映沥青路面轮廓幅值相较于基准线间的离散程度，其计算可参考式(5)(二维)和式(6)(三维)[6,11]；轮廓均方根偏差反映沥青路面轮廓高程点的差异程度，其计算可参考式(7)(二维)和式(8)(三维)[6]：

(5)

(6)

式中：y(xi)为xi处基于基准线的路面轮廓曲线高程点信息；其余参数意义同前文。

(7)

(8)

式中：y(xi)为xi处基于基准线的路面轮廓曲线高程点信息；其余参数意义同前文。

(3) 轮廓单峰平均间距S

轮廓单峰平均间距是表征路面二维宏观纹理间距的重要参数之一，亦可用于评定路面纹理的稳定性及耐磨性，其计算可参考式(9)及图7[15]。

(9)

式中：Si为相邻单峰最高点投影间距；N同式(2)。

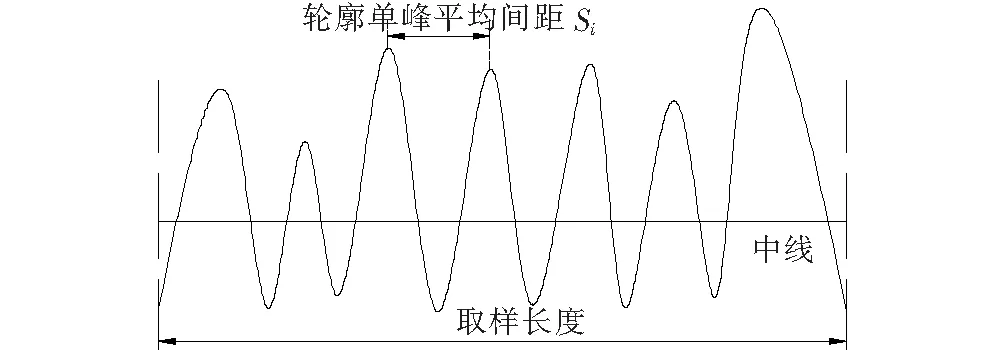
图7 轮廓单峰间距示意图

(4)轮廓算术平均波长λa和轮廓均方根波长λq

轮廓算术平均波长和轮廓均方根波长为表征沥青路面纹理间距特性的同类型参数，其计算可参考式(10)和式(11)[6,16]：

(10)

(11)

式中：Ra为沥青路面二维轮廓算术平均偏差；Rq为沥青路面二维轮廓均方根偏差；Δa为沥青路面二维轮廓算术平均斜率；Δq为沥青路面二维轮廓均方根斜率。

(5) 轮廓算术平均斜率Δa和轮廓均方根斜率Δq

轮廓算术平均斜率和轮廓均方根斜率为用于表征路面二维宏观纹理的同类型构造参数，其包含路面纹理幅值特性参数和间距特性参数，常用于表征沥青路面轮廓曲线峰(谷)的形貌特性，其计算可参考式(12)和式(13)及图8[16]：

(12)

(13)

式中：Δyi、Δxi分别为第i个极值点与第i-1个极值点高程点差值和沿中线方向差值。当第i点处为峰顶时，第i-1点处为谷底；N同式(2)。

图8 轮廓峰谷间距示意图

(6) 偏斜度Rsk

偏斜度是表征路面形状整体特性的重要参数，用于表征路面轮廓曲线的分布特性，即衡量路面轮廓曲线幅值相对于基准线的偏斜程度，其二维与三维的计算分别参考式(14)和式(15)[6]：

(14)

式中：Rq为沥青路面二维轮廓均方根偏差；y(xi)同式(5)；N同式(2)。

(15)

式中：Rq为沥青路面三维轮廓均方根偏差；z(xi,yj)、N、M同式(2)。

(7) 陡峭度Rku

陡峭度作为评价路面轮廓曲线整体特性的参数，常用于评价路面轮廓分布曲线相对于正态分布曲面形状的尖峭程度，其二维与三维的计算分别参考式(16)和式(17)[16]：

(16)

式中：Rq为沥青路面二维轮廓均方根偏差；y(xi)同式(5)；N同式(2)。

(17)

式中：Rq为沥青路面三维轮廓均方根偏差；z(xi,yj)、N、M同式(2)。

3.2 构造参数与摩擦系数的相关性分析

由上，该文选取并计算出基于数值路面纹路模型的平均断面深度、平均构造深度、轮廓算术平均偏差、轮廓均方根偏差、轮廓单峰平均间距、轮廓算术平均波长、轮廓均方根波长、偏斜度及陡峭度等构造参数。参考前文，可计算出路面纹理构造参数与仪摆值之间的Pearson相关系数以及Spearman相关系数，从而分析各构造参数与仪摆值的相关性强弱。因部分参数同时采用二维和三维的计算方法，对其相关性对比如图9所示。

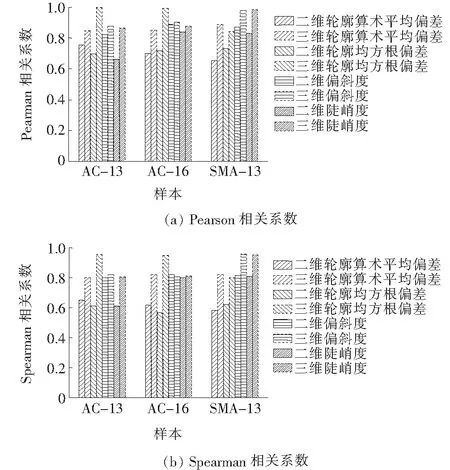
图9 部分二维、三维构造参数与仪摆值相关性柱图

由图9可知：利用Pearson相关系数与利用Spearman相关系数的评价结果相近。对于轮廓算术平均偏差、轮廓均方根偏差、偏斜度及陡峭度4种路面构造参数而言，三维参数与仪摆值具有更高的相关性。因此，该文选取部分二维路面纹理构造参数(平均断面深度、轮廓算术平均斜率、轮廓均方根斜率、轮廓单峰平均间距、轮廓算术平均波长、轮廓均方根波长)和部分三维路面纹理构造参数(平均构造深度、轮廓算术平均偏差、轮廓均方根偏差、偏斜度、陡峭度)分析其与试验仪摆值之间的相关性，结果如图10所示，同时进一步可分析各构造参数间的Pearson相关系数，结果如表1所示。

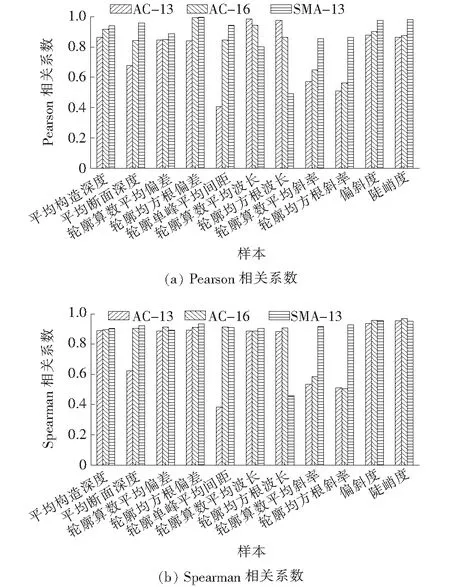
图10 整体构造参数与仪摆值相关性柱图

由表1可知：利用Pearson相关系数与利用Spearman相关系数的评价结果相近，所以下面分析以Pearson相关系数结果为主。

由图10(a)可知：

(1) 对于AC-13，轮廓单峰平均间距与仪摆值相关系数r介于0.3～0.5，二者间具有低度相关性；平均断面深度、轮廓算术平均斜率、轮廓均方根斜率与仪摆值相关系数r介于0.5～0.8，二者间具有中度相关性；平均构造深度、轮廓算术平均偏差、轮廓均方根偏差、陡峭度、偏斜度与仪摆值相关系数r介于0.8～0.95，二者间具有高度相关性；其余路面纹理构造参数如轮廓算术平均波长、轮廓均方根波长等与仪摆值相关系数r>0.95，二者间具有显著性相关性。

(2) 对于AC-16，轮廓算术平均斜率、轮廓均方根斜率与仪摆值相关性r为0.5～0.8，二者间具有中度相关性；轮廓均方根偏差与仪摆值相关性r>0.95，二者间具有显著相关性；其余路面纹理构造参数如平均构造深度、平均断面深度、轮廓算术平均偏差、轮廓单峰平均间距、轮廓算术平均波长、轮廓均方根波长、陡峭度、偏斜度与仪摆值相关性r为0.8～0.95，二者间具有高度相关性。

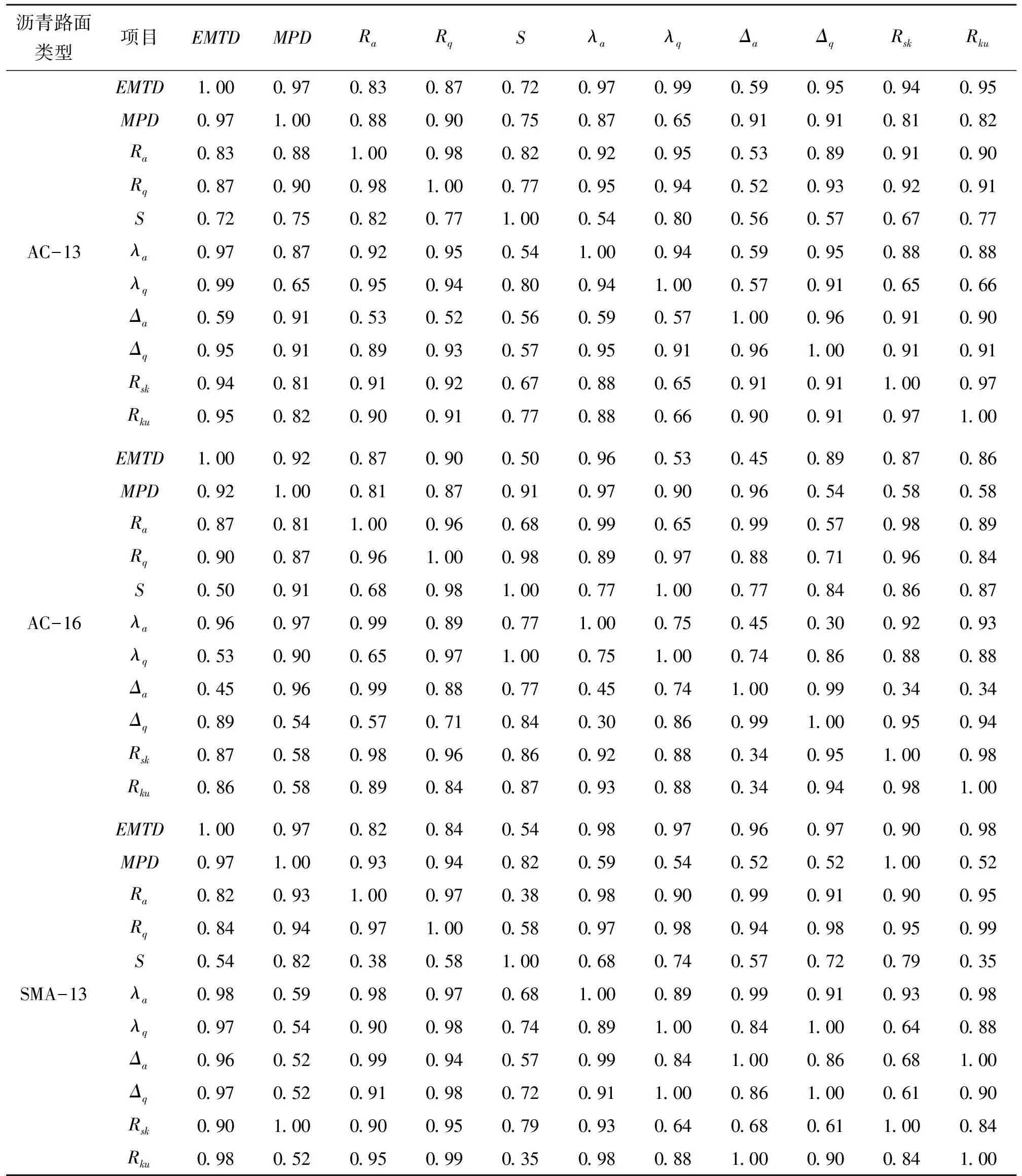
表1 各构造参数间Pearson相关系数

(3) 对于SMA-13，轮廓均方根波长与仪摆值相关性r为0.3～0.5，二者间具有低度相关性；平均构造深度、轮廓算术平均偏差、轮廓算术平均斜率、轮廓均方根斜率、轮廓单峰平均间距、轮廓算术平均波长与仪摆值相关性r为0.8～0.95，二者间具有高度相关性；平均断面深度、轮廓均方根偏差、偏斜度、陡峭度与仪摆值相关性r>0.95，二者间具有显著相关性。

由图10(b)可知：

(1) 对于AC-13，轮廓单峰平均间距、平均断面深度、轮廓算术平均斜率、轮廓均方根斜率与仪摆值相关性r<0.886，二者间不相关；其余路面纹理构造参数与仪摆值间相关性r>0.886，二者间显著相关。

(2) 对于AC-16，轮廓算术平均斜率、轮廓均方根斜率与仪摆值相关性r<0.886，二者间不相关；其余路面纹理构造参数与仪摆值相关性r>0.886，二者间显著相关。

(3) 对于SMA-13，轮廓均方根波长与仪摆值相关性r<0.886，二者间不相关；其余路面纹理构造参数与仪摆值相关性r>0.886，二者间具有显著相关。

分析表1可知：平均构造深度与轮廓算术平均波长、轮廓算术平均偏差与轮廓均方根偏差对3种沥青路面均呈现显著性相关。

综上所述，对于3种沥青路面，平均构造深度、轮廓算术平均偏差、轮廓均方根偏差、轮廓算术平均波长、偏斜度和陡峭度与其摆值间具有高相关性，可用于评价路面摩擦抗滑性能, 其中基于三维的构造参数：平均构造深度、偏斜度和陡峭度最值得推荐。

4 结论

该文通过基于光栅投影的结构光三维测量系统获取3种常见沥青路面纹理的高程点信息，利用Matlab软件重构沥青路面三维数据模型，在对比数值模型与试验参数的相关性从而验证模型的基础上，计算了不同构造参数(平均构造深度、平均断面深度、轮廓算术平均偏差、轮廓均方根偏差、轮廓算术平均斜率、轮廓均方根斜率、轮廓单峰平均间距、轮廓算术平均波长、轮廓均方根波长、偏斜度及陡峭度等)，并分析了各参数与摩擦试验结果[14]的相关性，得到以下结论：

(1) 利用基于光栅投影的结构光三维测量系统可较为精确地获取沥青混凝土路面表面纹理结构。

(2) 对比部分构造参数的二维表征和三维表征参数与仪摆值的相关性，轮廓算术平均偏差、轮廓均方根偏差、偏斜度及陡峭度的三维参数与样本试验仪摆值具有更高的相关性。

(3) 对于3种沥青路面，平均构造深度、轮廓算术平均偏差、轮廓均方根偏差、轮廓算术平均波长、偏斜度和陡峭度与其仪摆值间具有较高相关性，可用于评价路面摩擦抗滑性能, 其中基于三维的平均构造深度、偏斜度与陡峭度尤为推荐。

(4) 该文样本采取抽样方法获取，与实际中路面整体纹理状态会有一定的差异，这也是今后分析路面纹理参数与抗滑性能相关性需要关注的问题。