宽台阶对路堑高边坡变形破坏的阻断机制研究
张朔, 李斯涛, 李培锋, 尹小涛
(1.安徽理工大学 土木建筑学院, 安徽 淮南 232001; 2.云南玉临高速公路建设有限责任公司, 云南 昆明 650000;3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室, 湖北 武汉 430071)
随着“西部大开发”及“一带一路”等国家战略的实施,中国山区高速公路建设正在如火如荼地进行。山区高速公路路堑高边坡由于开挖深度大、危险程度高等特点,通常需要将边坡分级修建成台阶状,路堑高边坡的安全稳定对保障公路安全通行至关重要。
JTG D30—2015《公路路基设计规范》[1]对30 m以下岩质路堑边坡有明确的设计标准,但对于30 m以上的深挖路堑高边坡仅要求设计成台阶形,对于台阶的具体设计没有明确规定。当前实际工程中,一般按常规台阶对路堑高边坡进行设计,遇到问题通常采取不断放缓坡度、多次卸载刷方等方式稳定坡体,往往导致坡面汇水面积增大,且冲刷严重,给路堑高边坡施工过程及长期安全埋下隐患[2-5]。因此,需要探讨台阶对路堑高边坡安全稳定的作用机制。
目前国内外学者对路堑高边坡安全稳定性及失稳破坏机制等方面进行了诸多研究。王浩等[6-7]对超高路堑高边坡失稳机制及整治措施进行了研究;叶万军等[8-9]、高德彬等[10]通过资料收集、数值模拟等方法对黄土路堑高边坡进行了较为系统的稳定性分析及优化设计研究;宋从军等[11]、马思明等[12]对软质岩路堑高边坡的加固与防护进行了研究,对该类高边坡的综合治理进行了探讨;王婉[13]、刘小丽等[14]探究了二阶阶梯形均质边坡的开挖效应;言志信等[15]、黄诗渊等[16]采用数值计算方法研究了在地震作用下不同台阶宽度对边坡稳定性的影响,分析了边坡动力响应特性和边坡地震动力失稳机制;李建宇等[17]以某路堑边坡为例,探讨了锚索支护方案中的参数优化问题。在多台阶矿山排土场方面,GB 50771—2012《有色金属采矿设计规范》[18]对边坡台阶的分类较为细致,主要分为安全台阶、清扫台阶、运输台阶。规范中要求,安全台阶宽度不小于2 m,清扫台阶宽度不小于6 m,运输台阶宽度甚至达30~50 m,单级坡高度往往达到20~40 m[19-22]。
目前研究成果主要集中在路堑高边坡的失稳机制、加固与防护措施等方面。因此,能否在设计阶段对路堑高边坡的坡形进行优化,避免开挖过程中边坡失稳是当前路堑高边坡研究的重中之重。该文以云南省临沧市某路堑深挖高边坡为研究对象,采用现场工程地质调查、极限平衡法以及大型商用软件FLAC3D数值模拟等方法,通过在边坡设置不同位置和宽度的台阶,探讨宽台阶的最优位置和宽度,对比设置宽台阶与不设置工况的路堑高边坡的变形破坏差异,探讨宽台阶对路堑高边坡变形破坏的干预机制,为类似路堑高边坡加固提供支撑。
1 工程概况
1.1 工程简介
该路堑高边坡位于中国云南省临沧市境内,地处剥蚀溶蚀中山丘陵缓坡地貌,上覆残坡积黏土、粉质黏土,边坡防护横断面见图1。根据勘察设计资料以及现场踏勘,开挖边坡地层分为两层,自上而下分别为:① 粉质黏土,第四系全新世残破积,褐红色,硬塑,干硬,韧度中等,含少量岩石风化碎屑;② 泥岩,二叠系下统沙子坡组上段,灰红色,强风化,薄层构造,岩芯多呈碎块状。通过现场试验、工程类比及反分析综合确定了边坡岩土体物理力学性质指标,详见表1。
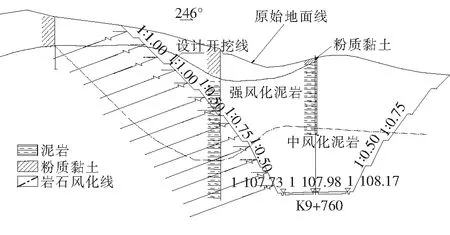
图1 深挖路堑边坡地质模型及防护横断面

表1 路堑高边坡岩土力学参数
1.2 边坡现状及潜在工程安全问题
根据施工记录和现场调查,第五级坡于2019年2月开挖,施工防护措施时在坡顶位置发现4条张拉裂缝,裂缝宽度约15、10、10、5 cm,裂缝长度约70、65、50、25 m。坡顶后方45 m处有一座220 kV高压输电铁塔,最外侧裂缝距高压铁塔约25 m。根据变形破坏迹象判断坡体已形成浅层滑面且处于欠稳定状态,若边坡处理不当将威胁高压铁塔安全性,进而影响电力系统正常运行。图2为坡顶构筑物及坡体现状。因此,有必要开展开挖造成的路堑高边坡失稳机理和宽台阶对高陡边坡的加固机理研究,为加固设计和优化提供支撑。
2 宽台阶最优几何参数的综合确定
2.1 二维计算模型及工况设计
基于图1所示边坡地质模型和表1各级次边坡岩土力学参数并考虑原地形及开挖坡形等,采用Rockscience系列中Slide 5.0模块在初始设计开挖方案的基础上建立数值模型,按照规范[1]要求,采用台阶式放坡,台阶宽度2 m。根据设计,将边坡自下到上依次分为7级,1~6级坡每层坡高10 m,7级坡坡高8 m。采用“上缓下陡”的坡率,符合地层土体强度自上而下增大的规律[9],其中7~5级坡的坡率为1∶1,4级坡、3级坡坡率为1∶0.75,2级坡、1级坡坡率为1∶0.5,建模范围详见图3。

图2 坡顶构筑物及坡体现状
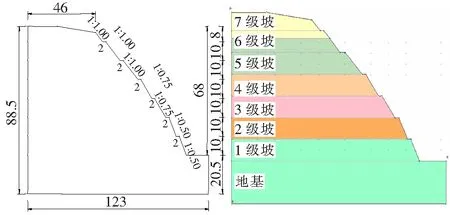
图3 二维计算模型示意图(单位:m)
在初始设计计算模型的基础上通过改变台阶位置和宽度对坡体稳定性系数的影响,以此综合判断台阶敏感位置及宽度。综合资源节约及经济性等方面的考量且实际工程中台阶形路堑边坡台阶宽度通常少见于10 m以上,多为2~5 m。因此该文将台阶宽度分别设置为3、5、7、10 m,并将增宽后的台阶分别置于2~7级坡坡脚位置,其余坡脚位置台阶宽度仍为2 m,共计24个计算模型。
2.2 宽台阶最佳宽度和最佳位置的确定
计算过程中采用简化Bishop方法将滑面剪入口控制在坡顶后方25 m(即现场调查最外缘裂缝处),剪出口控制在1级坡坡脚位置,自动搜索潜在滑面并计算安全系数。不同台阶宽度和位置下边坡整体稳定性系数演化曲线如图4、5所示。
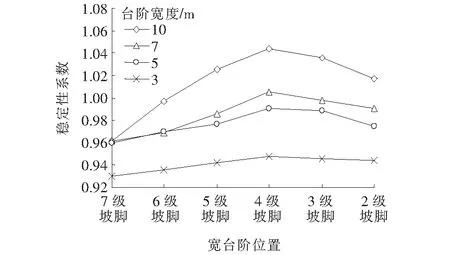
图4 不同台阶宽度下稳定性系数演化曲线
从图4可以看出:边坡稳定性系数随着宽台阶位置的降低,稳定性系数曲线均呈现出先增大后减小的趋势,且随着宽度的增加,曲线中间凸起更为显著,这些均证明将宽台阶设置于4级坡脚位置(边坡中部位置)最优,稳定性系数最大约1.04;7 m及以下宽度的台阶稳定性系数曲线几乎都在1.00稳定性系数之下,说明路堑高边坡整体相对不稳。原因在于,对高边坡来说,一般坡体中下部是阻滑段,中上部是下滑段,宽台阶设置在中部,对于高边坡相当于提供了卸载减荷作用;另外,中部宽台阶的施加使高边坡弱化为两个相对高度较低的次级边坡,因此稳定性系数达到最大,宽台阶再往下则效果降低。
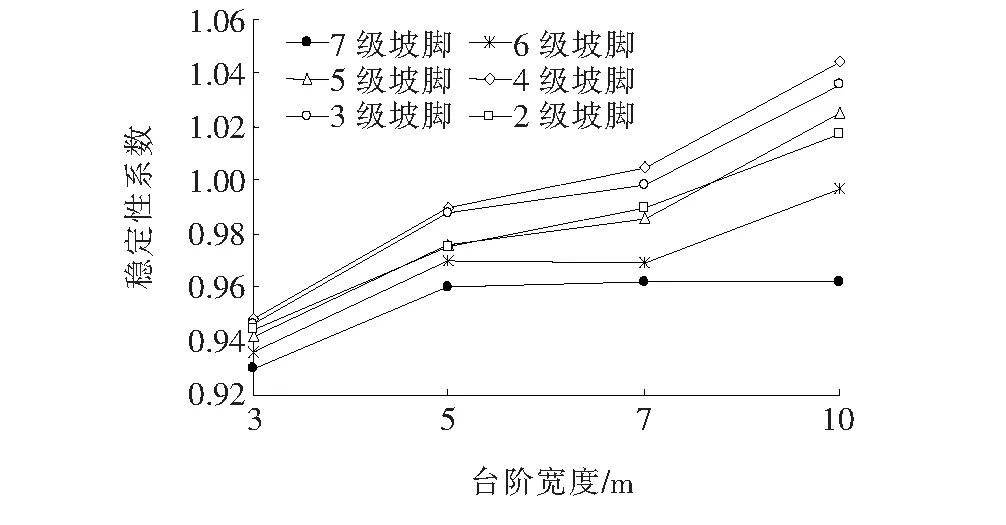
图5 不同台阶位置下稳定性系数演化曲线
从图5可以看出:随着台阶宽度的增大,边坡整体稳定性系数逐渐提高,且宽台阶位于第4级坡脚处时稳定性系数最高,台阶宽度从3 m增加至5 m以及从7 m增加至10 m,稳定性系数提高明显,而台阶宽度从5 m增加至7 m,稳定性系数提高程度不大。
从理论上讲,边坡平台的宽度越大,边坡的综合坡率越小,边坡越平缓,边坡的稳定性越高。但由于资源、经济、施加宽台阶的有效性等综合要素考虑,宽台阶仅能在有施作条件的地区采用,该文仅探讨其加固机理,为宽台阶的采用提供技术支撑,这也是对传统设计的有益补充和推进。
3 宽台阶对路堑高边坡变形破坏的阻断机制
3.1 三维计算模型及边界条件
在上述研究的基础上建立三维计算模型,采用大型商业软件FLAC3D仿真分析路堑高边坡开挖的变形破坏过程及宽台阶对高边坡变形破坏的干预机制。共设计4个三维计算模型:初始常规台阶设计方案(台阶宽度均为2 m)为工况1;4级坡坡脚台阶宽度5 m,其余台阶宽度2 m为工况2;4级坡坡脚台阶宽度10 m,其余台阶宽度2 m为工况3;6级坡坡脚和四级坡坡脚台阶宽度5 m,其余台阶宽度2 m为工况4。相应的计算模型如图6所示。
三维模型均采用六面体网格划分,网格类型为Quads&Triangles,考虑模型计算效率及精度,保证最大网格尺寸为2 m×2 m。边界条件采用边坡模型底面固定约束,侧面法向约束,表面自由。边坡材料参数详见表1,计算采用理想弹塑性本构模型,破坏准则选取Mohr-Coulomb屈服准则[23]。计算过程中通过移除单元体实现土体分层开挖。

图6 三维计算模型示意图
三维工况1用于分析开挖造成的高边坡变形破坏过程;工况1~3用于对比分析宽台阶对高边坡破坏机制的影响;工况2、4用于对比分析宽台阶个数变化对高边坡变形破坏的影响。三维计算工况见表2。

表2 三维数值计算工况
3.2 常规台阶下开挖变形破坏过程及稳定状态变化
路堑高边坡滑裂面的产生及失稳破坏是一个动态过程。在FLAC3D中通过移除各级边坡单元体模拟实际边坡开挖过程,图7、8分别为工况1下边坡开挖过程中不同开挖步对应的塑性区及最大剪应变增量揭示的边坡变形破坏过程。
在高边坡开挖初期,开挖面附近岩土体主要以坡脚应力集中,剪切破坏为主,开挖卸荷回弹显著;剪切塑性区范围主要集中在各级坡坡脚及坡面位置,随着边坡开挖深度的加大,剪切塑性区逐渐向坡体中上部延展扩大,坡顶附近出现小范围张拉塑性区,边坡临近极限状态,各级近坡面塑性区逐渐连通,塑性区出现明显分界面。坡体开挖完成后,塑性区完全贯穿坡体,坡顶后缘出现大量张拉塑性屈服区。

图7 塑性区云图揭示的边坡变形破坏机制
从图8可以看出:边坡的变形失稳过程是由于开挖卸荷过程中应力释放,边坡岩土体应变逐渐积累,滑裂面从坡脚位置初步形成并逐渐向坡体内部延展扩大最终贯通的过程。在开挖初期,开挖卸荷导致每一级坡均在坡脚位置出现剪应变集中,与上述塑性区分布情况相吻合,说明坡脚位置容易产生塑性变形和剪应力集中,属于边坡薄弱部位。随着开挖深度的增加,剪应变集中带逐渐扩大,并逐渐发育成剪切滑裂面,主滑面最终贯穿坡体。坡体全部开挖完成后,出现4个潜在剪切滑面,剪入口位于坡顶后方13~26 m处,剪出口分别位于5级坡至2级坡坡脚处,潜在滑裂面深度6~20 m,最大剪应变为0.006 7。潜在滑面的位置均为现场调查时裂缝出现的位置,间接说明了数值模拟中计算参数选取和模型搭建的正确性。
从边坡开挖过程中塑性区及剪应变变化情况来看:其变形破坏大致分为3个阶段:前期卸荷回弹阶段、中期剪切破坏阶段和后期整体失稳破坏阶段。采用每10 m坡高增设一个宽2 m的台阶平台的初始常规设计方案,开挖过程中形成明显的主滑裂面,边坡无法保证自稳。

图8 最大剪应变增量云图揭示的边坡变形破坏机制
3.3 台阶宽度对路堑高边坡破坏机制的影响
为对比分析宽台阶对高边坡破坏机制的影响,探讨台阶宽度对路堑高边坡破坏机制的干预作用,图9(a)、(b)、(c)分别为工况1、2、3开挖完成后的塑性区云图。
从图9可以看出:在高边坡中部施加宽台阶后边坡塑性屈服范围明显减少,仅宽台阶上部部分坡体塑性区贯通,坡体内以及浅层坡面以剪切破坏为主,坡顶一定范围内主要发生张拉破坏。
在宽台阶作用下,塑性区范围于宽台阶处被分解为上下两部分。随着台阶宽度增加,坡体内的剪切塑性区深度明显减小并逐渐向各级边坡坡脚上方的坡面贴近,对坡体深部土体的扰动有所减轻,高边坡的整体破坏趋势得到分解,宽台阶下部稳定性有明显改善。设置宽台阶后,虽然将边坡的整体破坏分解,但是对于宽平台上部的各级边坡干预作用并不明显,上部坡体失稳风险程度仍然很高。

图9 台阶宽度对破坏形态的改变
为了探讨宽台阶对路堑高边坡潜在滑面及破坏深度影响,图10(a)、(b)、(c)分别为工况1、2、3开挖完成后最大剪应变增量云图。
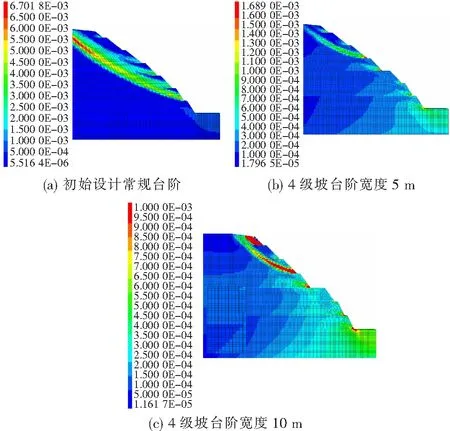
图10 不同台阶宽度下最大剪应变增量云图对比
从图10可以看出:施加宽台阶后,贯穿整个坡体的深层滑裂面被阻断成上部坡体的浅层滑裂面,滑裂面的范围及深度有所减小,宽台阶下的各次级边坡仅在坡脚位置出现应力集中,说明宽台阶的施加有效地阻断了边坡整体滑裂面的形成,路堑高边坡的破坏由整体破坏分解为局部破坏。
从定量方面分析,工况2潜在滑裂面剪入口位于坡顶后方9~15 m处,剪出口位于5级坡脚处,潜在滑裂面深度5~12 m,最大剪应变增量为0.001 7,较初始设计常规台阶降低74.6%。工况3潜在滑裂面剪入口位于坡顶后方7~14 m处,剪出口位于5级坡脚处,潜在滑裂面深度5~10 m,最大剪应变增量为0.001,较初始设计常规台阶降低85.1%,且7级坡处剪切塑性区范围和最大剪应变急剧增大,出现应力集中现象,考虑到坡顶上覆土体性质弱,且开挖方量过大,这些是其破坏的原因。
在高边坡中部设置宽台阶,边坡整体破坏被分解,说明宽台阶对边坡的开挖变形破坏具有显著的阻断机制,通过增加台阶的宽度,使得原本已经设计成常规台阶的边坡再次分级,边坡的整体破坏分解为两个局部破坏,在一定程度上减小了边坡失稳的规模,降低了整体破坏的风险,提高了边坡的整体稳定性,改善了边坡的自稳能力。
3.4 宽台阶对路堑高边坡破坏的阻断机制
工况4在工况2的基础上在6级坡脚增设一个宽5 m的宽台阶,形成“宽窄台阶交替”的台阶形式。从开挖完成的塑性区对比图(图11)中可以看出:随着宽台阶个数的增加,剪切塑性区范围在宽台阶处明显减小,边坡上部塑性区贯通趋势得到分解,仅在6级坡和5级坡附近形成小范围连通区域,且尚未贯穿坡体,坡体上部的整体破坏被分解。

图11 宽台阶对破坏形态的改变
从开挖完成后的最大剪应变增量对比图(图12)中可以看出:在第6级坡脚增加宽台阶后,有效地阻断了在5级坡脚处产生的潜在滑裂面,改善了上部坡体的稳定性。随着开挖深度的加大,仅在各坡脚处出现应力集中,未形成明显的剪切滑裂面。
将路堑高边坡设计成“宽窄台阶交替”的台阶状边坡优于工程中常见的“常规台阶”形式和“中部超宽台阶”形式。主要原因如下:
(1) 在常规台阶的基础上间隔增设宽台阶,可将高边坡弱化成多个高度相对较低的独立坡体,可以有效地分解高边坡整体破坏趋势,使坡体内部应力优化分布,避免应力集中现象,对提高坡体稳定性、减少边坡破坏区域等方面均有一定优势。
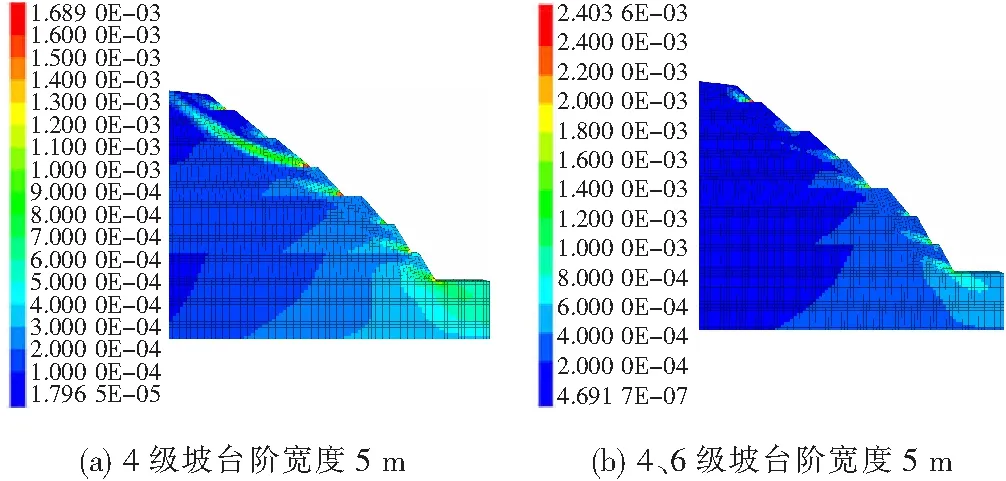
图12 不同宽台阶个数下最大剪应变增量云图对比
(2) 可在多个宽台阶处增设截排水措施,雨水通过坡面径流汇集到宽台阶处得到有效分流,有效减少坡面冲刷及径流量,避免雨水下渗,有利于坡体稳定性提高。
(3) 施加宽台阶可以有效降低坡面小型滚石滑落风险,起到一定缓冲作用,有助于高边坡施工及道路通行安全。
4 宽台阶作用下的费效比分析
由于上覆土层岩土力学性质较差,常规台阶直接开挖将导致边坡整体失稳破坏,即使考虑宽台阶作用,边坡虽不至于整体失稳,但也要看到其整体处于欠稳定状态,安全保障依然不足。因此,仍需在分阶段开挖中及时采取加固措施,且加固措施的深度需要加强。在原有锚索框格梁加固方案下,探讨不同加固措施的费效比和加固效果。
根据初始设计选择采用4种不同类型的锚索,分别编号为L1、L2、L3、L4。锚索水平射入角为20°,7级坡至5级坡锚索(L3、L4)布置横坡向间距为4.0 m,纵坡向间距为3.0 m,5级坡以下锚索(L1、L2)布置横坡向间距为3.0 m,纵坡向间距为3.0 m。L1、L3型锚索由4束公称直径为15.2 mm钢绞线组成,L2型锚索由10束公称直径为15.2 mm钢绞线组成,L4型锚索由6束公称直径为15.2 mm钢绞线组成。锚索框格梁规格为500 mm×500 mm,由于在锚索布置中存在横坡向间距3.0 m和4.0 m两种情况,因此选取12.0 m横坡向宽度开展开挖方量和加固措施量化对比分析。工况1常规台阶锚索布置图见图13。锚索设计参数见表3。
将该加固措施分别施加至工况2、3、4,经计算,结果均满足安全稳定性评价标准。挖方量自道路中线左侧计算,开挖深度取12 m。表4为不同工况下初始设计加固前后边坡稳定性计算结果及开挖方量统计。

图13 常规台阶锚索布置图
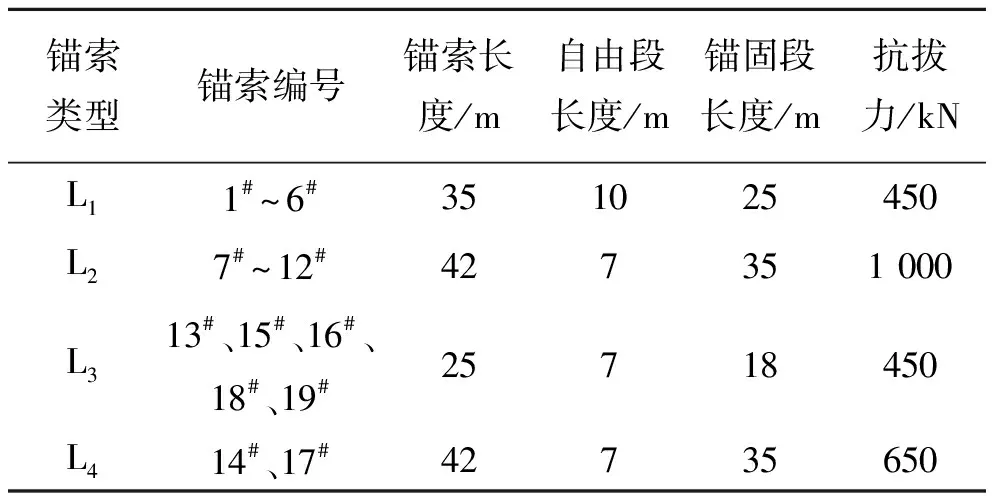
表3 常规台阶锚索参数设置

表4 初始设计加固前后边坡稳定性计算结果及挖方量
从表4可以看出:在保证边坡稳定的前提下,若工况2、3、4施加与常规台阶工况1采取相同的加固措施,计算结果偏于保守。经过反复试算综合确定不同工况的最优加固措施方案,工况2在常规台阶锚索布置的基础上将3、4级坡锚索纵坡向间距调整为5.0 m;工况3、4在常规台阶的基础上将1级坡至4级坡锚索纵坡向间距均改为5.0 m。经验算调整后各工况仍满足边坡稳定性要求。各工况调整后的加固措施见图14。加固措施调整后的边坡稳定性计算结果见表5。不同工况下边坡加固所需锚索量见表6。
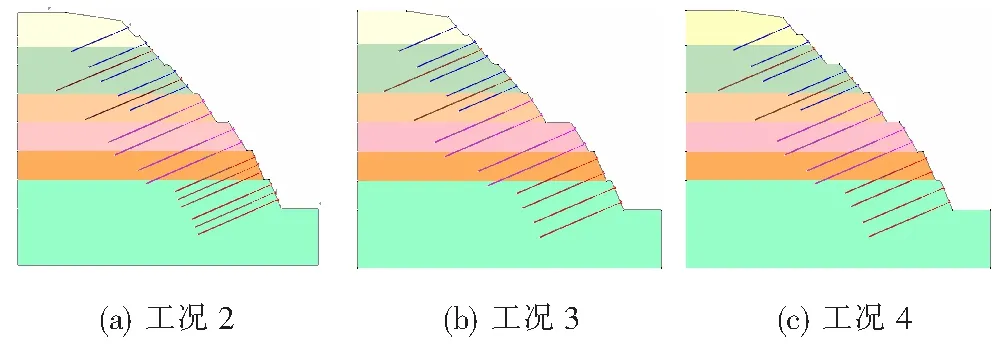
图14 不同工况下锚索布置图

表5 加固措施调整后边坡稳定性计算结果

表6 不同工况下边坡加固所需锚索数量
通过对比各工况挖方量与加固所施加的锚索量,发现随着台阶宽度的增加及宽台阶个数的增多,挖方量的增加为初始设计挖方总量的5.0%~13.6%,锚索数量的减少为初始设计总锚索数量的20.4%~27.2%。采用工况4“宽窄台阶交替”的设计方案总体挖方量增加约为初始常规台阶设计总挖方量的7.3%,锚索减少量为总锚索量的27.2%,且“宽窄台阶交替”的设计方案相较其他设计有诸多优势,一方面能够有效地提高路堑高边坡的自稳能力,将边坡的整体破坏趋势分解;另一方面,可以减少边坡加固措施的用量,节约工程开支,为最优设计方案。
5 结论
依托出现问题的实际工程路堑高边坡案例,探讨了宽台阶对边坡的加固机理,同时探讨了宽台阶的最大效能加固方案,所得结论如下:
(1) 宽台阶造成的稳定性系数演化曲线揭示宽台阶的施作位置以中部为佳,宽度不是越大越好,均存在最佳位置和最佳宽度。
(2) 塑性区和剪应变增量云图揭示的路堑高边坡的变形破坏可以分为3个阶段,即前期卸荷回弹阶段、中期剪切破坏阶段和后期整体失稳破坏阶段。
(3) 由设置宽台阶和设置常规宽度台阶的路堑高边坡塑性区和剪应变增量云图对比分析发现:宽台阶对路堑高边坡的整体变形破坏具有显著的阻断效果。宽台阶加固效果显著,机理在于边坡中上部为滑移段,中下部为阻滑段,中上部的卸荷作用是其阻断机制的力学本质,即高边坡分解为几个有限高度边坡,从而实现风险管控的目标。
(4) “宽窄台阶交替”的设计方案可以使坡体内部应力优化分布,有效减少坡面冲刷,降低坡面小型滚石滑落风险,优于“常规台阶”和“中部超宽台阶”方案。
(5) 通过费效性对比发现,设置宽台阶后挖方量的增加为初始设计挖方总量的5.0%~13.6%,锚索用量的减少为初始设计总锚索用量的20.4%~27.2%。经过多种工况对比,该路堑深挖高边坡工程在第4、6级坡脚分别设置宽度为5 m的“宽窄台阶相结合”为最佳设计方案。

