基于Logistic模型的多车道高速公路左侧硬路肩设置判据

林小媛 朱顺应 李维吉 肖文彬 王 红

(武汉理工大学交通与物流工程学院 武汉 430063)

0 引 言

分析我国现有八车道高速事故数据发现，随着车道数增加，交通量增大，有变道需求的车辆进行变道引起的事故率增加[1]．因此，建议多车道高速公路设置左侧硬路肩．有研究发现，多车道高速公路设置左侧硬路肩有助于提高通行效率并降低事故风险[2-3]，互通匝道设置2.5 m宽左侧硬路肩可降低互通事故率[4]．

美国高速公路设置左侧硬路肩情况较为普遍，其研究也主要集中在路肩的使用模式、通行效率、安全影响等方面[5-6]，而缺少对设置条件的研究．由于道路土地资源的局限，高速公路沿线条件受限而无法全线设置，故提出左侧硬路肩设置判据，建立判断变道事故率高低的预测模型，初步判断是否设置左侧硬路肩．

现有研究通常采用二分Logistic回归模型分析交通事故与各影响因素之间的关系[7-8]．戢晓峰等[9]构建了二元Logistic模型探究人、车、路和环境等因素对事故严重程度的影响．郝志国[10]获取变道过程中车辆间TTC、速度、加速度等冲突相关参数和指标，选取Logistic模型建立变道冲突预测模型．而对于交通冲突安全评价，Gallelli等[11-13]利用VISSIM、SSAM分别对交叉口、城市快速路合流区交通冲突安全进行评价．

综上，现有文献研究重点为运用Logistic研究交通事故与各影响因素之间的关系，构建相关事故预测模型，并未对左侧硬路肩的设置判据进行研究．文中以广深高速为例，针对多车道高速公路是否设置左侧硬路肩提出判据，基于Logistic模型，将变道事故率高低作为判断模型的因变量，通过累计频率法得到临界值，建立变道事故率高低预测模型，初步判断各互通是否设置左侧硬路肩，并通过VISSIM仿真和SSAM安全评价对初步判断不建议设置的互通进行左侧硬路肩“有-无”交通冲突差异分析作进一步识别．

1 左侧硬路肩的设置分析

据统计，高速公路上由于单车爆胎、超速、措施不当等引起的交通事故占事故总数的37.5%．而Pei等[14]进行的调查表明：高速公路上事故最常见的原因之一是改变车道，至少30%的碰撞发生在车辆改变车道或离开道路时．

基于左侧硬路肩在多车道高速公路中的重要安全作用，在有条件时应考虑全线设置，但是国内早期的高速公路均未考虑日后左侧硬路肩的建设，在进行改扩建时将受到诸多沿线控制因素的影响，无法保证所有路段满足左侧硬路肩连续设置的宽度需求，因此要建立设置左侧硬路肩的条件判断模型．本文将变道事故定义为：不设置左侧硬路肩的多车道高速公路内侧车道上突然出现故障或燃油耗尽等有紧急临时停车需求的车辆转移至右侧路肩的过程中发生的事故，不同情况下左侧硬路肩的设置结果见表1．

表1 左侧硬路肩设置推荐

2 方 法

1) 运用Logistic建立变道事故率相对高低预测模型，初步判断是否设置左侧硬路肩．

将变道事故率的高低作为因变量y，当变道事故率处于高水平时，y=1，反之y=0．假设有n个影响因素与变道事故率的高低有关，记为x=(x1,x2,…,xn)，则在n这个影响因素下的Logistic数学模型：

(1)

(2)

P2(y=0)=1-P1(y=1)

(3)

式中：P1、P2为变道事故率高或低的概率；xi(i=1,2,…,n)为变道事故率高低的影响因素，为自变量；β0为常数项；βi(i=1,2,…,n)为回归系数．

2) 运用VISSIM和SSAM仿真安全评价对初始判别不建议设置的互通进行左侧硬路肩“有-无”交通冲突差异分析作进一步识别，弥补了事故率高低预测结果的相对性，使设置判据更合理．

3 Logistic模型

3.1 数据与变量选取

3.1.1数据采集

选取广深高速为研究对象，该高速全长122.8 km，设计车速120 km/h，全线共设置25个互通，其中莞番—新联、太平—五点梅、福永—鹤洲已改扩建为双向十车道，其余互通为双向六车道．采集了2017—2019年各互通发生的事故数据，数据由交警现场执法记录，信息包括事故所在车道、事故原因、事故形态等内容，人工逐条对每起事故案情事实进行分析，界定是否属于变道事故，共筛选出1 739条数据．以半年为统计周期，计算各互通的变道事故率，共150例．

3.1.2自变量的选取

综合国内外的相关研究[15-16]，考虑路段宏观客观因素，从路段交通流、道路环境中选取相关自变量进行研究．

1) 平均交织程度 高速公路互通间车辆变道会产生交织，形成较为复杂的交通状态，影响车道上车辆的行驶．交织区交通流图见图1．

图1 交织区交通流

则平均交织程度计算公式为

(4)

式中：Vw=Vw1+Vw2，交织区段中的总交织交通量，pcu/h；Vw1为两交织流中较大的交织交通量，pcu/h；Vw2为两交织流中较小的交织交通量，pcu/h；V=V1+V2+Vw，交织区段中的总交通量，pcu/h；L为互通间长度，km．

2) 货车比例 货车比例计算公式为

(5)

式中：Vtruck为路段上货车标准交通量，pcu/h；Vsum为路段上总交通量，pcu/h．

3) 路段v/c比 路段v/c比是在理想条件下，最大服务交通量与基本通行能力之比，其计算公式为

(6)

式中：v为高速公路在规定服务水平下的最大服务交通量，pcu/h；c为规定服务水平下的基本通行能力，pcu/h．

4) 平面线形均衡指标 平面线形均衡指标α又称平面线形偏转指标，表征路线的弯曲程度(路线弯曲影响行车舒适性)，为

(7)

式中：αi为道路曲线偏转角，rad；L为路段长度，km．

5) 纵断面线形指标 纵断面线形指标主要考虑累积相对势能变化指标：

(8)

6) 车道数 车道数即路段包含的车道数，为x6．

3.1.3因变量的界定

对于事故率高低的临界值判断，通常以累计频率曲线的突变点来确定．累计频率曲线法常用于道路事故多发路段鉴别[17]．

累计频率法计算步骤如下.

步骤1将150例变道事故率(起/km)数据划分为(0～1、1～2、…、9～10)10个组别，然后统计变道事故率为n的路段个数，并计算相应的发生频率和累计频率，事故频率统计结果见表2．

表2 累计频率曲线法统计结果

步骤2对拟合函数求导处理得到斜率变化最大点以确定变道事故率高低划分界线．对数据进行累计频率分析，可得到图2的变道事故率频率累积图．

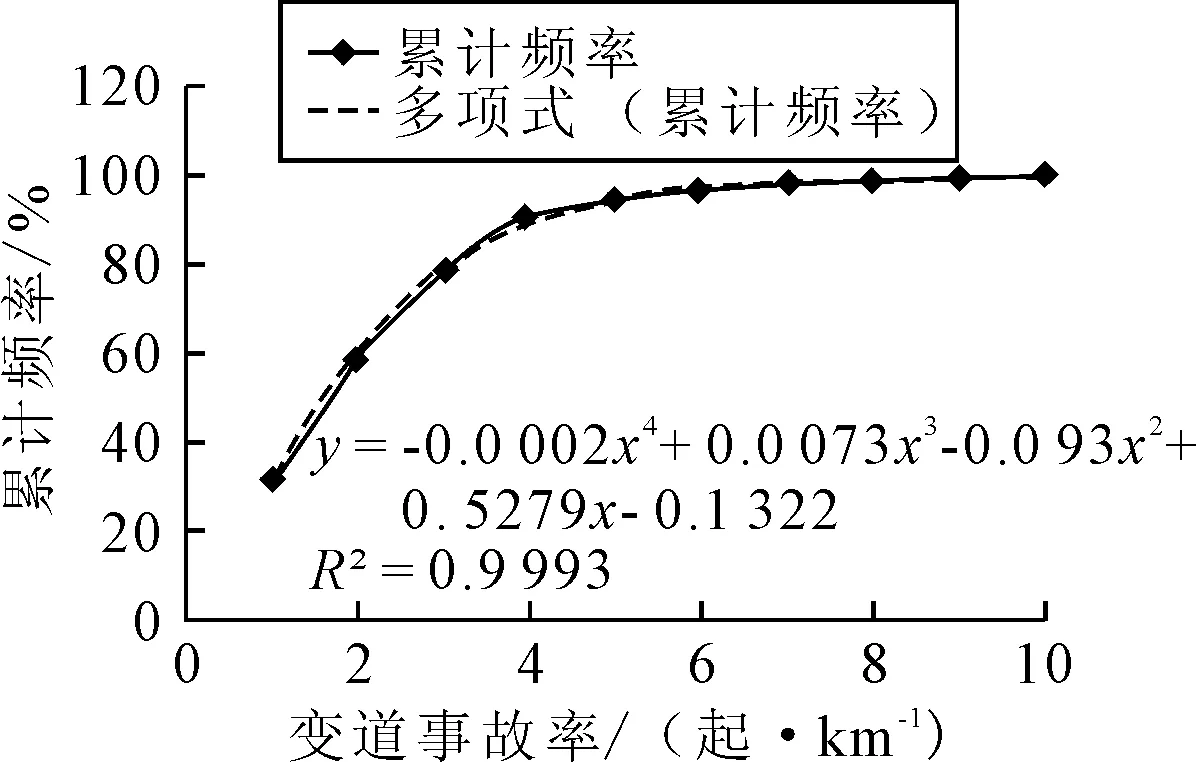
图2 变道事故率累计频率曲线

对拟合曲线计算最小半径位置，极值点位置是(5.26，0.967)，因此将5.26作为划分变道事故率相对高低的临界值．

3.2 模型的标定、分析与检验

3.2.1模型的标定与分析

对自变量采用混合逐步选择法，取显著性水平0.05，得到平均交织程度，货车比例，v/c比，相对势能4个指标与变道事故率的高低显著相关，见表3．

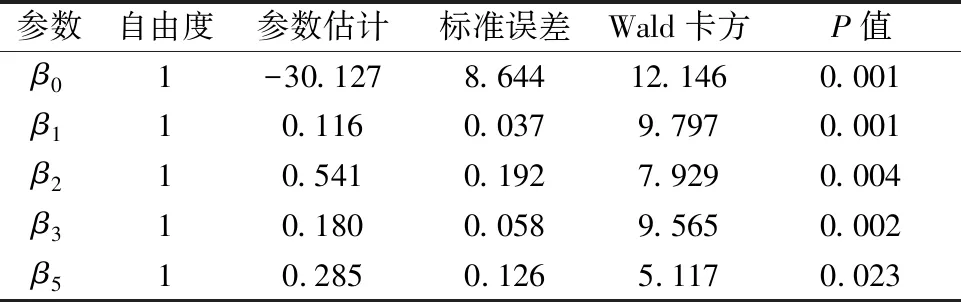
表3 参数估计结果

得到变道事故率高低的Logistic模型：

P1(y=1)=

(9)

由表3可知:平均交织程度、货车比例、v/c比和相对势能的参数估计值均为正值，表示路段平均交织程度、货车比例、v/c比和相对势能的值越大，发生高变道事故率的概率就越大．

表4为各自变量的优比估计，包括点估计和95%Wald置信区间估计两部分．点估计部分是在其他条件不变的情况下，其中一个自变量增加一个单位发生高变道事故率的概率为原来的某一数值倍，可以看出货车比例增加一个单位发生高变道事故率的概率最高，是原来的1.719倍．95%Wald置信区间则给出了在其他条件不变的情况下，某一自变量变化一个常数单位时相应的发生比的倍数改变区间．

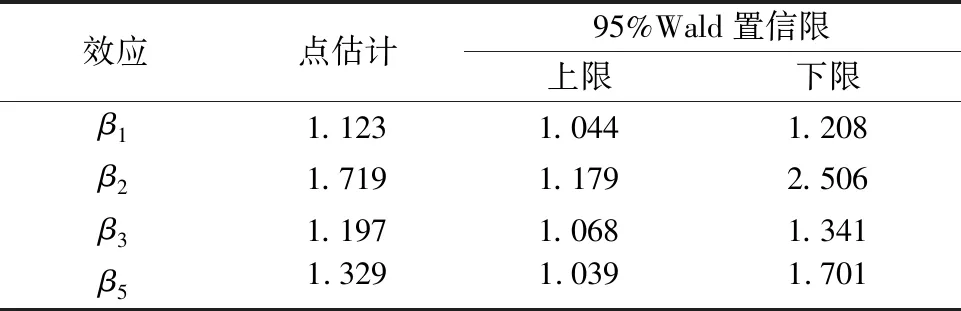
表4 发生比率的置信区间

3.2.2模型的检验

1) 模型拟合优度检验 模型拟合优度检验有Pearsonχ2统计量、D统计量和Hosmer-Lemeshow统计量．χ2统计量，D统计量近似于χ2分布，在样本方面要求包括：①每一协变量类型中至少有10例观测；②80%的协变量类型要有五个以上预测事件数；③在余下的协变量类型中，预测事件数应大于2．从这些要求来看，当自变量数量增加时，尤其是连续型自变量纳入模型之后，χ2统计量和D统计量不适合用来检验模型拟合优度，故本文采用Hosmer-Lemeshow指标来进行拟合优度检验．

Hosmer-Lemeshow指标是一种类似于Pearsonχ2统计量的指标，其统计公式为

(10)

Hosmer-Lemeshow拟合优度检验，通过Pearsonχ2来概括这些分组中事件结果的观测数和预测数，然后将其与自由度为G-2的χ2分布进行比较，结果见表5．

表5 Hosmer-Lemeshow拟合优度检验

由表5可知：在显著性水平α=0.05的条件下，χ2检验不显著，因此模型很好地拟合了数据．

2)模型预测准确性检验 序次相关指标的准确度检验结果见表6．由表6可知：本次研究共有2025个数据对，其中和谐数据对占91.2%，不和谐的数据对占8.8%，没有结．Somer’s D、Gamma、Tau-a、c四个序次相关指标值中，除了Tau-a指标，其余三个指标值都大于0.7，表示模型具有较强的预测能力．

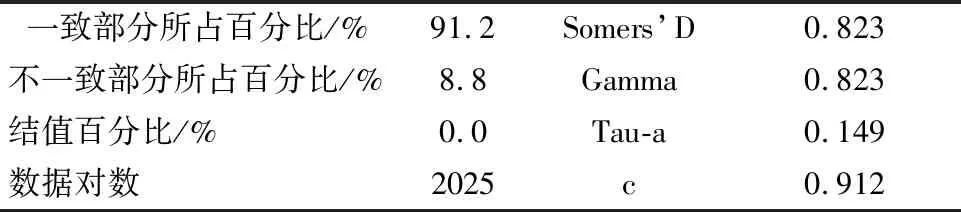
表6 序次相关指标的准确度

3.3 模型的应用

选取《广深高速改扩建可行性研究报告》中2045年预测的相关自变量的数据，带入模型进行拟合．根据模型结果，得到广深高速火村-萝岗、连莞番-新联、太平-五点梅、福永-鹤洲这4个互通间的变道事故率处于高水平的概率大于0.5，其他互通处于高变道事故率的概率均小于0.5，故建议这四个互通优先设置左侧硬路肩，宽度不足时建议改变路基形式，其余互通宽度不足时可不设置左侧硬路肩，见图3．

图3 广深高速预测数据拟合结果

4 VISSIM、SSAM仿真安全评价

不设置左侧硬路肩的多车道高速公路上故障车辆从最内侧车道变道至右侧硬路肩的过程中产生的冲突类型主要为两种：追尾冲突和变道冲突．故通过交通冲突评价进行左硬设置安全分析与评估．图4为冲突示意图．

图4 冲突示意图

对于交通冲突安全评价替代指标，现阶段较为广泛应用的主要是时间碰撞(TTC)和后侵入时间(PET)[18]；对于交通冲突评价方法，现场观测得到的冲突数据精度较低且难以保证鲁棒性[19]，交通仿真则能模拟实际交通状况，提供各种测试场景，获得的冲突数据能够对各种设定条件下的道路交通安全进行评价，故利用广深高速互通纵坡、路段长度等实测数据及《广深高速改扩建可行性研究报告》中2045年预测的交通量等相关数据，运用VISSIM仿真对初步判别不建议设置左侧硬路肩的互通进行“有-无”交通冲突分析作进一步判断．这里对建议设置的互通也一并仿真，但只是将其结果作为比较之用．设计两组实验，一组为不设置左侧硬路肩，一组为设置左侧硬路肩．在交通安全替代评价模型SSAM中设置TTC和PET的参数阈值，导入两组仿真实验的车辆运行轨迹，分析结果见图5．

图5 仿真实验冲突数结果

由图5可知：建议设置的互通交通冲突减少比例均大于20%，平均冲突减少42.45%，不建议设置的互通减少比例均小于10%，差异不大，故建议不设置左侧硬路肩．

虽然各互通设置左侧硬路肩均有减少交通冲突提高安全性的效用，但广深高速公路全线路侧城镇化程度高，路网、管网密集，多个路段平面拓展受限，因此很多路段无法为修建左侧硬路肩提供充足的空间．故设置左硬后交通冲突减少幅度较小的互通，在左侧宽度拓展受限时可不设置左侧硬路肩，具有一定经济性．若设置左硬后冲突减少幅度较大且宽度受限时，建议采取更改路基形式如将整体式车道改成立体分离式的方案．

5 结 论

1) 建立基于Logistic的变道事故率相对高低预测模型初步判断各互通是否设置左侧硬路肩，运用VISSIM和SSAM仿真安全评价模型对初步不建议设置的互通作进一步判断．

2) 以变道事故率的高低为因变量，从交通流、道路环境条件中选取六个自变量建立Logistic模型，得到平均交织程度、货车比例、路段v/c比和相对势能与因变量显著相关，并对自变量的发生比进行了解释．对模型进行Hosmer-Lemeshow拟合优度检验，采用序次相关指标对模型预测准确性进行检验，检验结果表明建立的模型拟合度和预测准确度都处于较好的水平．

3) 将Logistic模型运用于即将进行改扩建的广深高速各路段左侧硬路肩设置研究中，结果显示火村—萝岗等四个互通间变道事故率处于高水平的概率大于0.5，建议优先设置左侧硬路肩．运用VISSIM及SSAM仿真安全评价对初始判别不设置的互通进行左侧硬路肩“有-无”交通冲突分析，结果显示交通冲突减少比例低于10%，故建议不设置左侧硬路肩．

本文仅从路段交通事故相对高低和有无左侧路肩交通冲突变化大小等安全角度出发，研究了整体式多车道高速公路左侧硬路肩的设置判据，“有-无”交通冲突差异分析弥补了累计频率法的不足，适用于改扩建初期缺乏沿线拓宽拆除成本数据的情况，后续将会考虑更多元化的变道情况并结合改扩建高速公路的建设成本等方面从工程经济角度完善设置方案研究．