智能共享停车供需匹配优化模型及改进蜂群算法

何胜学

(上海理工大学管理学院 上海 200093)

0 引 言

随着泊车服务机器人(parking valet robot，PVR)的推广应用和无人驾驶技术的不断发展，过去车辆和泊位在车辆停泊期间固定搭配的共享停车供需匹配方式亟待调整改变以适应时代的发展需要．PVR和无人驾驶车辆(autonomous vehicle，AV)一方面使车辆在停泊期间变换车位成为可能，从而实现车辆停放时空布局的合理化，减少泊位闲置的时间碎片，提升泊位利用率．另一方面也提出了“如何合理规划PVR和AV的移车操作避免不必要的车辆移位，从而减少相关的运行成本，并降低在车辆移位过程中发生事故的风险”的问题．为解决上述问题，文中将以预约式共享停车中同时存在泊车期间不允许移位、允许利用PVR移位和AV自主移位三种差异化停车需求为背景，在满足可接受的共享停车需求条件下，以最小化车辆移位次数和移车成本为目标建构共享停车供需匹配模型，并利用模型可行解(即车辆与泊位的时空匹配关系)结构特征设计一种蜂群优化算法对模型进行求解．

近年来学者们针对共享停车进行了居多研究：

1) 针对共享停车需求特征与影响方面 文献[1]通过时间序列预测时间重要度，在匹配时尽量减少热点时间的预约，从而减少泊位空闲时间碎片．文献[2]提出停车设施的选择概率依赖于设施的停车吸引力系数、停车收费、相关步行时间和实际行程时间．文献[3]提出将停车需求分布与路径选择决策相结合．文献[4]分析了不同情境下泊位拥有者参与共享泊位的意愿．文献[5]实证分析共享无人车的使用对停车泊位需求的影响．文献[6]提出基于个人信用风险等级来匹配泊位．文献[7]分析了共享停车供给与需求存在的不准时特征．文献[8]比较了泊位利用率和停车需求者满意度对共享泊位匹配的影响．

2) 以构建车辆与泊位的匹配模型和优化共享停车服务平台服务方面 文献[9]以共享停车平台收益及用户步行距离为优化目标，构建了预约请求下共享泊位分配模型．从参与各方经济利益最大化角度出发，文献[10]构建了基于拍卖机制的共享停车泊位分配、定价和收益机制．文献[11]通过定义虚拟泊位概念建立了共享停车泊位匹配的优化模型．文献[12]在多个停车场的共享停车泊位匹配中考虑了停车需求的优先级别差异．文献[13]在综合租用车位成本、提供停车服务收入和拒绝潜在用户的损失基础上，构建了车位租用和停车需求分配的统一决策模型．文献[14]以步行距离的差异定义共享车位的异质性，构建了跨区域泊位分配的随机动态规划模型．文献[15]利用滚动时域方法对实时获得的共享停车供需进行滚动式动态匹配．文献[16]以最大化泊位利用率和减少步行距离为目标，建立的共享停车的泊位分配模型．文献[17]通过分析停车需求的到达时间和停泊时长分布，确定最佳共享泊位与保留非共享泊位的数量．

3) 针对无人驾驶对共享停车的影响方面 文献[18]分析了无人车市场占有率、燃油费和停车费对无人车在完成载客后选择停车场的影响，建议通过差异化的区域收费引导无人车的停车场选择，从而在整体上实现停车的供需平衡．文献[19]分析了在不同的停车能力限制条件下共享无人车的市场占有率对早上通勤出行的影响．文献[20]利用仿真模型对共享无人车、私有无人车、共享有人车和非共享有人车共存情况下的停车需求变化进行分析，发现共享车辆的存在可降低总体停车需求，但也会增加部分敏感区域的停车需求．文献[21]分析了停车管理策略对需求响应式共享无人车的规模、服务效率和公平性，以及相关的外部性影响．文献[22]对智慧停车和自动代客泊车理论发展与相关实践进行了系统梳理，明确了当前相关领域需要关注和解决的主要问题．

与现有研究相比，本研究的特色体现在：①首次在共享停车研究中同时引入PVR和AV的影响，为共享停车在新时代发展提供理论支持；②与现有研究主要关注停车场选择和AV路线规划不同，本研究则关注车辆停泊过程中的移位操作和相关的成本；③针对新建匹配模型的NP-hard特征，利用车辆与泊位时空匹配关系与蜜蜂基因序列进行类比，并通过匹配交换操作体现蜂群优化中工蜂对幼蜂的抚育，最终实现针对本文匹配模型的蜂群优化算法设计．

1 模型建构

1.1 基本假设条件

本研究的基本假设条件如下：①研究针对预约式共享停车的需求与供给匹配，因此假设相关的车辆停车需求时间和泊位可供共享停车的开放时间事先已知；②为了方便构建模型，假设所有车辆的停车需求时间和共享泊位的开放时间均是整块连续的时间段；③假设不同类别车辆对泊车过程中是否允许变换泊位的要求事先已知；④假设共享泊位之间进行车辆泊位变换的行车路线长度已知；⑤为了减少不必要的移车操作，假设不管是利用泊车机器人移车还是无人驾驶车辆的自主移位均只能在车辆停车需求时间和泊位共享开放时间的起止时刻发生．

考虑到假设条件⑤，有必要将共享停车服务的总时间加以分割，形成长度较短的分割时间段，进而将车辆的停车需求和泊位的供给也对应分割为小的时间段．具体的时间分割方法如下：①首先利用所有车辆停车需求时间的起止时刻和共享泊位开放时间的起止时刻构成一个起止时刻集合；②剔出上述起止时刻集合中的重复元素，并按照时间的升序对剩余元素加以排序，得到一个有序的起止时刻序列；③比照上述有序的时刻序列，以序列里的时刻作为起止时刻，将所有的车辆的停车需求时间和共享泊位的开放时间划分为连续相接的具有较小长度的分割时间段．

1.2 参变量简介

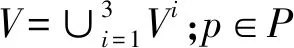
1.3 匹配模型

下面给出具有多种车辆差异化停车需求的供需匹配优化模型.

(1)

(2)

(3)

(4)

目标函数(1)由两个加和项构成，其中第一个加和项是所有车辆发生移位的移位路线总长度，第二项是不同车辆发生泊位改变时引发的惩罚性系统成本之和．为了满足第一类不允许在泊车过程中进行泊位变换的停车需求，对应的单次惩罚性系统成本w1的值应该远大于其他两个惩罚性成本量w2和w3．从共享停车服务平台或管理者的角度出发，w2的值应大于w3，因为利用PVR的成本一般是由平台承担的，而无人驾驶车辆的移位成本一般由车辆所有者承担．约束(2)为如果一个泊位在给定分割时段不提供共享停车服务，则该时段没有需要共享停车的车辆停于该泊位；而当该泊位在该给定分割时段提供共享停车服务时，至多只能有一辆需要共享停车的车辆停于该泊位．约束(3)为在给定时段任意给定车辆的共享停车需求应得到满足．约束(4)为对决策变量取值范围的限定．由目标函数(1)和约束(2)～(4)构成的模型(1)～(4)完整描述了多车种条件下共享停车供需匹配问题．

如果先对约束(2)和(3)分别在泊位集合P和车辆集合V上进行加和，然后加以比较，为

(5)

式(5)为在任意给定分割时间段，车辆的停车需求小于泊位的供给．将满足式(5)的车辆共享停车需求称为可接受的合理需求．显然在允许对所有车辆进行泊位变换的条件下，一定存在一个可行的供需匹配满足约束(2)和(3)．

利用定义在分割时间段上的车辆停车需求与泊位共享停车供给可定义相关的基于分割时段数量的泊位利用率φ为

(6)

模型(1)～(4)属于纯整数二次规划．从约束和目标函数的特征可知，也可将模型(1)～(4)视为一类特殊的二次分配模型．已有研究表明二次分配问题属于一类极难的NP-hard问题，目前相关的一些线性化技术只能改善问题求解过程中的目标下界，不能在现实可接受的计算时间内得到并确定较大规模二次分配问题的全局最优解．鉴于上述知识，下文将针对模型(1)～(4)设计一种有效的启发式算法，以期迅速高效地得到问题的近似最优解．

2 启发式算法设计

2.1 模型解与蜂群优化概念的映射关系

定义2(基因):如果为Vk中的每一辆车在集合Pk中选择一个独占的泊位来在分割时间段k停放该车辆，则将会在Vk和Pk之间建立一个可行的匹配关系，其中的匹配构成一个对应分割时间段k的匹配集合，记作e(Vk,Pk)或ek．在蜂群优化里称ek为蜜蜂的第k个基因．

由基因的上述定义可知，如果两个相异匹配m(k1,v1,p1)∈ek和m(k2,v2,p2)∈ek, 那么k1=k2=k,v1≠v2,p1≠p2．由于基因包含的匹配存在上述关系，因此易知ek对应约束(2) 和(3)．为了方便后续的表述，我们用Ek表示ek的取值范围．

定义3(蜜蜂):对应分割时段集合K={1,2,…,k,…,nK}的nK个基因序列组成一个向量，称为一个蜜蜂，记作h=(e1,e2,…,ek,…,enK)．由匹配和基因的定义以及两者与模型约束的关系可知，对于任意一只蜜蜂h存在一个唯一的模型可行解x与之对应．把对应蜜蜂h的模型可行解记为x(h)．而将利用式(1)计算得到的-z(x(h))称为蜜蜂h的适应值．

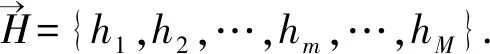
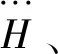
(7)

ψnew=ψ-Δψ

(8)

λnew=αλ

(9)

当基因集合已满(已经包含ρ只雄蜂的基因序列)或蜂王的能量接近0时，一次繁育飞行结束，蜂王将返回蜂巢去孵化幼蜂．如果完成繁育飞行时，蜂王的基因集合未满，则从当前备选蜂集合中选取适应值相对较大的备选蜂的基因序列来填满基因集合．

(10)

蜂王返回蜂巢后孵化幼蜂包含两种情况:一种情况为通过将蜂王基因序列与基因集合中雄蜂基因序列进行类似遗传算法的交叉和变异操作得到一定数量新的幼蜂;另一种情况是仅对蜂王的基因实施变异操作得到一定数量新的幼蜂．两种情况下得到的幼蜂会形成幼蜂群．幼蜂群的规模限定为M．

蜂群优化算法将工蜂的对幼蜂的抚育投射为对新生幼蜂实施特定的启发式操作，以期改进幼蜂的适应值．基于上述基本理念，我们设计了如下的启发式操作．假设存在两个匹配m(k,v1,p1)∈ek和m(k,v2,p2)∈ek, 对其实施交换操作Γ，可得到交换后两个新的匹配m(k,v2,p1)和m(k,v1,p2)．上述交换操作Γ为

Γ(m(k,v1,p1),m(k,v2,p2))→

m(k,v2,p1),m(k,v1,p2)

(11)

(12)

在新设计的蜂群优化算法中，将工蜂对一只幼蜂的抚育定义为从该幼蜂的基因序列中随机选取一个基因，实施式(12)所示的多次交换操作，用每次操作得到的新基因替换幼蜂对应的基因，并计算对应的适应值．选择适应值最大的交换操作序列作为最终的交换操作，并用得到的新基因替代幼蜂的原始基因．上述针对幼蜂基因的系列交换操作在蜂群优化中对应现实中工蜂对幼蜂的抚育．

2.2 蜂群优化求解步骤

基于2.1给出的概念和操作，下面给出蜂群优化算法的具体操作步骤.

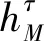
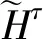
步骤4繁育飞行．令ψ=Rand(10,20)×Δψ和λ=500+Rand(0,500)．这里Rand(a,b)为在区间[a,b]上均匀分布的一个随机整数．按照2.1介绍的繁育飞行操作，实施繁育飞行．

步骤5孵化幼蜂．将蜂王基因序列与基因集合中雄蜂基因序列进行类似遗传算法的交叉和变异操作得到一定数量新的幼蜂；然后仅对蜂王的基因实施变异操作得到一定数量新的幼蜂；将两种情况下得到的蜜蜂组合形成规模为M的幼蜂群．

步骤6工蜂对幼蜂的抚育．按照2.1介绍的启发式操作实现工蜂对幼蜂的抚育．

步骤7更新蜂群．用新生成的幼蜂群替代原有的蜂群，并清空蜂王的基因集合，转步骤2．

3 算例分析

算例为19辆车和12个泊位的共享停车匹配问题．在19辆车中，前5辆属于第一类停泊中不允许移位的普通车辆，第6到第9辆属于第二类可利用泊车服务机器人进行移位的普通车辆，其他车辆属于第三类无人驾驶车辆．车辆的停车需求时段的起止时间见表1，而泊位的共享停车开放时段的起止时间见表2．假设对应第一、第二和第三类车的惩罚性系统成本分别为100，20，10 min．泊位之间的移位距离矩阵L见式(13)．算例分析中，距离和惩罚性成本的单位均设为km．按2.1的时间分割法，共得到38段连续的分割时间段．基于分割时段的泊位利用率φ为0.789 7．

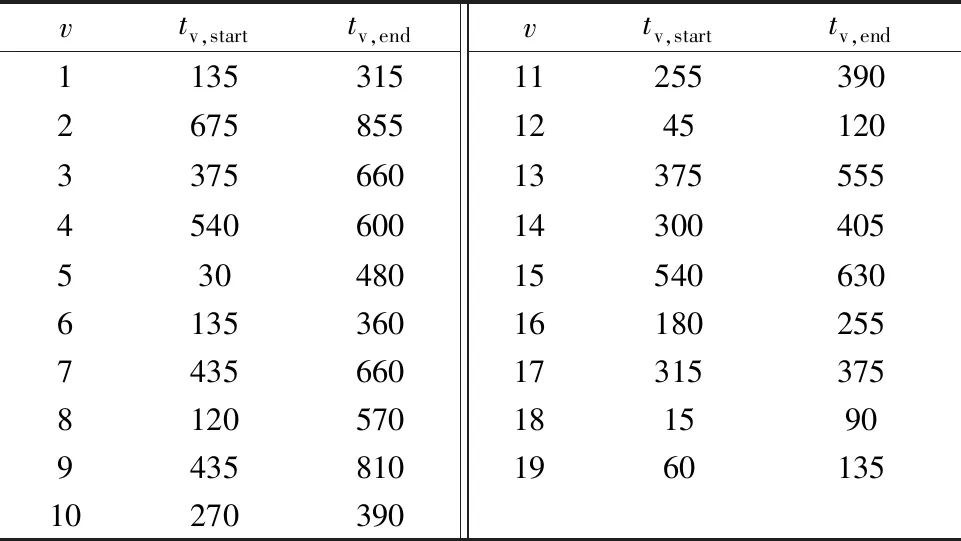
表1 车辆停车需求 单位：min

表2 泊位共享开放时间 单位：min

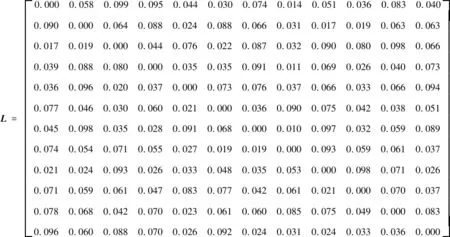
(13)

设定蜂群优化算法的相关参数值如下：M=20、ρ=10、Δψ=10、α=0.6、θ=20、Pmute=0.015、n=5和NIteration=500．利用Java语言实现蜂群优化算法，并在NetBeans IDE平台运行，利用的计算机处理器具有intel Core i5 4 GB内存，运行具有500次迭代的算法一次所需要的计算时间小于(1/1 000) s．图1为利用蜂群优化求解上述问题的3次典型运算结果．在三次运算中，最初的蜂王对应的目标函数值分别为4 285.53、4 264.87和4 345.66，而经过500次迭代，最优目标函数值分别降至70.28、70.14和70.19．由图1中最优目标函数值的变化可知:蜂群优化具有较高的计算效率，可以在迭代的初期迅速得到较好的近似最优解，但在算法迭代的后期，对目标函数的改善幅度逐渐减少．由图1可知:三次运算具有相似的收敛特征，因此说明蜂群优化算法具有很高的可靠性．由于启发式算法的计算效果会随着相关参数值的改变而变化，也与具体的问题相关，因此要在实际应用时得到好的算法表现，就需要对参数进行灵敏度分析．鉴于目前尚缺乏实证数据，将在后续研究中在这方面再作深入分析．

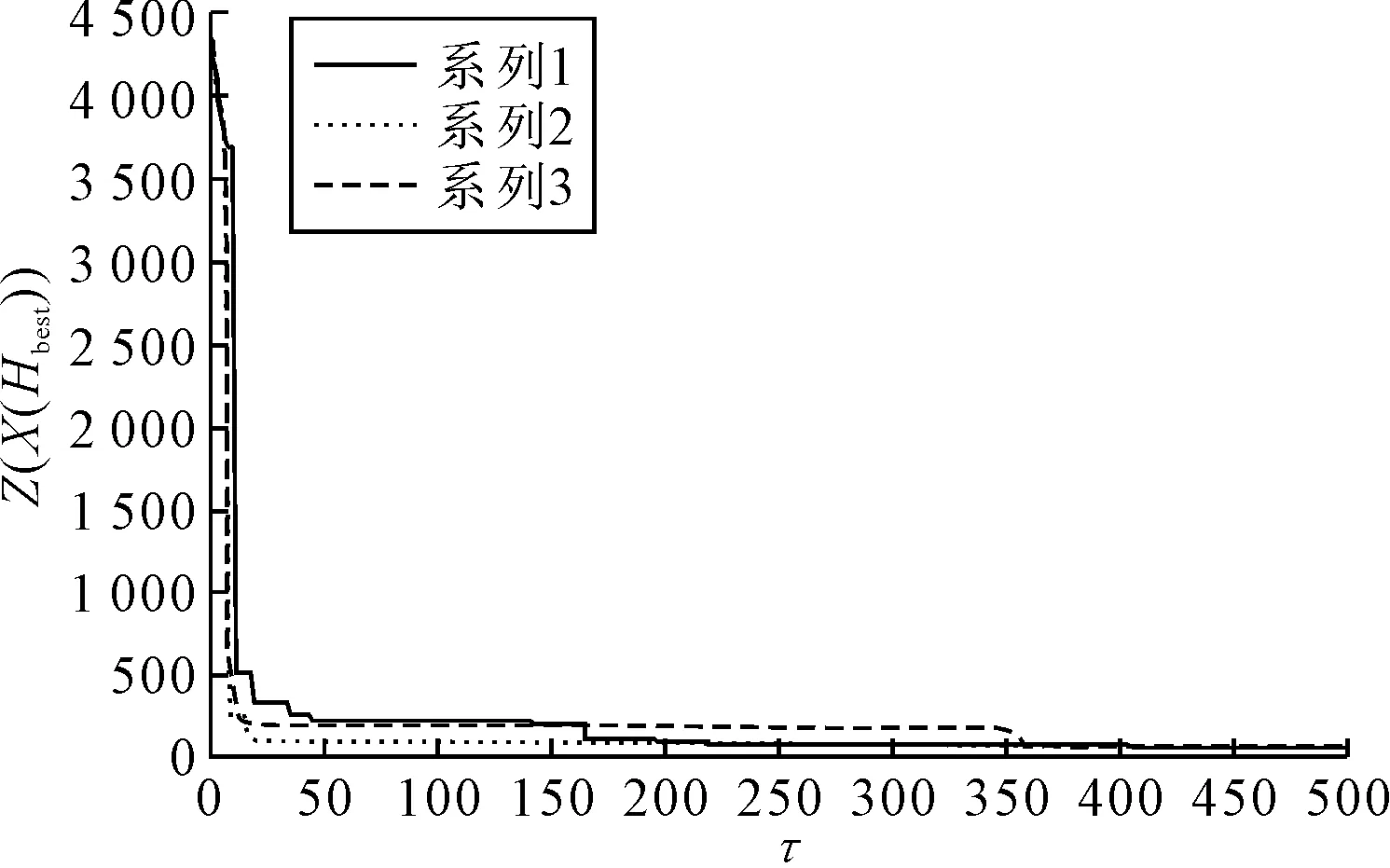
图1 随迭代次数τ增加而变化的最优目标函数值z(x(hbest))

与图1中系列1的数据对应，最终的车辆与车位时空匹配结果见图2．图中第一列第一行的“sn”为第一列为泊位的序号．该矩阵图的第一行的数字表示分割时段的序号．矩阵图中其他元素的意义规定如下：“/”为对应泊位在对应分割时段不开放；“_”为对应泊位在对应分割时段为共享停车开放，但是没有被占用；数字“n” 为对应泊位在对应分割时段被序号为n的车辆占用．由图2可知:车辆7、8、9均需移位一次，对应的总惩罚性成本为60；而车辆10也需要移位一次，对应的惩罚性成本为10．上述结果与最终的70.28的目标函数值一致．进一步观察可知，车辆9的需求必须通过泊车机器人的移位操作才能得以满足．

图2 最佳匹配的矩阵图

表3为程序运行12次的统计学结果．将12次结果的最终目标函数值进行升序排列，从而使出现的相同结果更易被观察．从12次结果的均值和标准方差可知蜂群优化算法具有很高的可靠性．

表3 程序运行12次的统计学结果

4 结 论

1) 通过时段划分和设定恰当的移位惩罚性系统成本，可以将复杂的停车供需时间匹配关系简化为分割时段上的供需匹配，从而使建立的预约式共享停车的供需匹配模型简洁有效．

2) 新设计的蜂群优化算法可以有效求解本文的共享停车模型，优化的最终结果仅为初值的1/60．

3) 泊车机器人的使用可以使原本无法满足的停车需求得以满足，进而提升泊位的利用率．

4) 设定不同的惩罚性系统成本可以在最终匹配结果中满足各类车辆不同的停车需求．