随机风浪中破损船横摇与瘫船倾覆概率计算
赖国锐 毛筱菲 詹星宇
(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (武汉理工大学高性能舰船技术教育部重点实验室2) 武汉 430063)
0 引 言
在随机横风横浪的共同作用下,失去动力的船舶会在产生横荡运动的同时横摇至一个大角度,导致船上的开口进水,造成船舶失稳甚至倾覆.目前,IMO已经制定了针对完整船舶瘫船稳性的第一层、第二层衡准,并提出了瘫船稳性失效模式的直接评估指南.近年来,国内外学者对瘫船稳性直接评估方法展开了大量研究.Belenky等[1]使用LAMP水动力学程序计算不规则横浪中船舶的倾覆概率.Umeda等[2]研究了包含“横荡-垂荡-横摇-纵摇”的耦合数值模型,但缺乏对非定常风的考虑.Kubo等[3]对Umeda的方法进行了完善,建立了不规则横风和横浪作用下的四自由度模型,并将计算结果与物理实验结果进行了比较.王新宇等[4]基于SDC1/INF.6的瘫船薄弱性衡准相关内容,研究了瘫船状态的船舶因货物移动而具有不同初始横倾角时的倾覆概率变化情况.胡丽芬等[5]将破损船舶进水过程的时域计算和倾覆概率计算相结合,探究了不同载况下破损船舶在进水过程中稳性高度和倾覆概率的关系.王田华等[6]建立了四自由度耦合数学模型及船舶水动力系数数据库,运用非线性时域预报方法对船舶的整个倾覆过程进行模拟计算.在2019年SDC 7-5会议中,IMO建议采用至少包含“横荡-垂荡-横摇-纵摇”四自由度耦合运动模型进行船舶的运动模拟,但采用多自由度运动模型时为达到可信度要求需要计算的样本量很大,导致多自由度耦合模型难以应用.
文中在现有的瘫船稳性直接评估方法研究基础上,根据横摇运动时历对船舶在随机横浪中的横摇幅值进行统计分析,对处于横风横浪中不同破损形式船舶的横摇运动进行时域模拟,并运用蒙特卡洛方法计算破损船瘫船状态的倾覆概率.通过比较破损船与完整船的横摇运动特性和倾覆概率,对船舶破损造成的稳性损失进行系统评估.
1 横风横浪中时域横摇运动模型
随机横风横浪中船舶瘫船状态的时域横摇运动方程形式为
Mwind(t)+Mwaves(t)
(1)
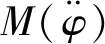
1.1 非线性横摇阻尼力矩


(2)
1.2 非线性复原力臂
船舶作大角度横摇运动时,复原力臂曲线的非线性可能是导致其横摇过大而倾覆的原因之一.此外,不同舱室破损形式会影响船舶复原力臂曲线的形状,如舱室不对称浸水会导致船舶复原力臂曲线不经过原点.文中采用准静态模拟法计算完整船舶和破损船舶的复原力臂曲线,并采用高次多项式拟合用于后续船舶横摇运动的模拟.
1.3 风倾力矩
船舶受到的随时间变化的风倾力矩表达式为
χ(ωn))·AL·HC·cos2φ(t)·{1-sinφ(t)}
(3)

(4)
(5)
(6)
式中:Nw为规则波数量;ωn为波浪圆频率;εn为分布在[0,2π]的随机相位;HS为有义波高.
1.4 波浪力矩
波浪力矩考虑复原扰动力矩,其计算公式为
(7)

(8)
(9)
式中:k为波数;δω为波浪频率间隔;HS为有义波高;TZ为平均过零周期.
2 破损船舶瘫船倾覆概率计算方法
船舶破舱中最普遍的进水情况为第三类舱室破损进水.该类舱室破损后,舱的顶盖在水线以上,舱内外的海水相连通且水面保持一致.对于第三类舱室破损进水,宜采用损失浮力法计算破损船舶的浮态以及稳性.舱室进水使船舶损失部分浮力,船体将会下沉以获得补偿浮力,同时产生一定的倾斜,当船体下沉和倾斜后的浮心与重心重新共垂线时,船舶将处于新的平衡状态,并认为船舶的排水量和重心位置保持不变.
不考虑进水过程的影响,采用四阶龙格库塔法在时域内求解破损船舶的单自由度横摇运动方程,并运用蒙特卡洛方法计算船舶在不同风浪环境条件下的倾覆概率.对于船舶瘫船倾覆概率的计算,可以通过大量的单自由度时域模拟得到足够的样本容量n,统计时域模拟中船舶发生倾覆的次数nc来计算船舶的倾覆概率p,即有:
(10)
当样本容量n足够大时,可认为其近似服从正态分布N(p,(1-p)),其置信区间为
(11)
IMO SDC 7-5文件的直接评估指南中建议α′取0.05,即置信度为95%,由正态分布表可以查得zα′/2的数值.为使置信度达到95%,同时误差值不超过5%,根据统计学中随机抽样样本容量设计方法[7],结合后续计算所取的环境条件,文中的船舶模拟计算的样本数取为1 000次.在数值模拟中,若船舶横摇角超过实际倾覆角度,则认为船舶发生倾覆.IMO将实际倾覆角度定义为船舶进水角、稳性消失角和50°的较小者,文中取实际倾覆角为50°,每次时域模拟的时间为1 h,若倾覆发生,则该次时域模拟结束.
3 计算算例分析
文中研究对象为DTMB5415,其主要船型参数见表1,两种破损形式分别为第三类舱室破损的对称浸水和不对称浸水(仅右舷浸水)形式,破损舱信息[8]见表2.实海域中船舶航行时需安装舭龙骨以减小船舶横摇角,舭龙骨长47.3 m、宽0.65 m.图1为破损船舶示意图.

表1 DTMB5415主要船型参数

表2 DTMB5415破损舱信息 单位:m

图1 破损船舶示意图
3.1 CFD求解横摇阻尼系数
采用CFD软件STAR-CCM+模拟DTMB5415的横摇自由衰减运动.数值模拟中缩尺比为1∶51,将船模置于静水中,给予一定的初始横倾角,并记录船模横摇角随时间变化的曲线.
由于船模作自由衰减运动时的横摇幅值较大,需采用重叠网格设置.将计算区域分为背景区域和重叠区域两大部分.背景区域中的出口边界类型设置为压力出口,入口、底部、顶部以及左右两侧面均设置为速度进口,见图2a).重叠区域中的船体表面设置为壁面,其余边界的类型设置为重叠网格.在网格加密方面,对自由液面进行加密,以提高流体特征的分辨率,同时在大于重叠区域的背景区域中应进行圆柱型的局部加密,设置加密尺寸与重叠区域的网格尺寸相近,以防止重叠网格在随船体横摇发生旋转运动时与背景网格之间出现插值错误,见图2b).在重叠区域中,对于船体变化特征较明显的区域进行网格加密,以细化几何.

图2 CFD模拟设置
以DTMB5415完整船模(无舭龙骨)为对象,设置初始横倾角为28°,通过改变网格数量(疏网格、中等网格、密网格数量分别为106万、222万、493万)以及时间步长(分别取0.001 s和0.002 s)进行网格及时间步长的敏感性分析.采用CFD进行模拟的结果与实验结果相比,见图3,其横摇幅值误差和横摇周期误差均小于3%,说明CFD模拟船模的横摇自由衰减运动具有较高的准确性,且可以看出不同的网格数量以及时间步长对船模的横摇运动模拟结果的影响小.综合考虑计算资源,选取中等网格方案、时间步长为0.002 s作为后续计算的设置方案.
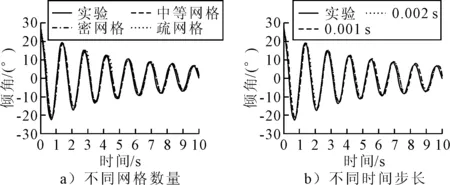
图3 模拟结果与实验结果对比
采用该设置方案分别模拟DTMB5415(无舭龙骨)的完整状态、对称浸水形式、不对称浸水形式(初始横倾角分别为28°、19°、0°)的横摇自由衰减运动,得到横摇消灭曲线见图4.将根据横摇消灭曲线计算得到的实船的线性横摇阻尼系数α(1/s)、平方横摇阻尼系数β(1/rad)和池田法计算结果进行比较,见表3.

图4 横摇消灭曲线
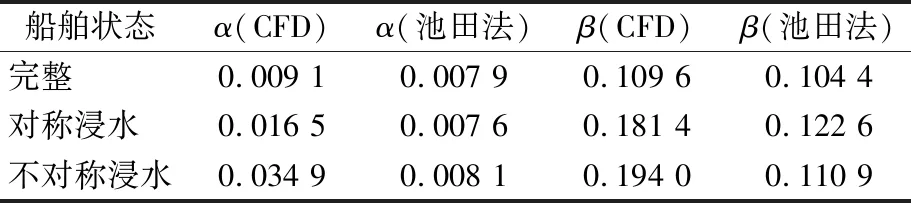
表3 CFD和池田法计算的横摇阻尼系数对比
由表3可知:采用CFD方法和池田法分别计算完整船舶的横摇阻尼系数时,两者的计算结果比较接近,说明采用池田法计算完整船的横摇阻尼系数是可行的.但当采用池田法计算破损船的横摇阻尼系数时,计算结果要明显小于CFD方法得到的结果,这是由于池田法使用船舶的船型参数计算横摇阻尼系数,没有计及破损舱室内液体振荡产生的水舱阻尼对船舶横摇阻尼的影响[9].因此,目前一些文献[10-11]采用池田法计算破损船舶的横摇阻尼,其计算结果会与实际结果有较大误差,应当通过模型试验或者CFD模拟以获得较为准确结果.
实际海域中船舶安装舭龙骨可以有效减少船舶的横摇,采用CFD方法继续模拟DTMB5415(带舭龙骨)的横摇自由衰减运动,计算得到船舶的横摇阻尼系数和横摇周期见表4.

表4 DTMB5415(带舭龙骨)横摇阻尼系数和横摇周期
3.2 规则波中船舶横摇运动模拟及验证
计算得到的DTMB5415复原力臂曲线和采用“等效船舶”法计算的有效波倾系数曲线见图5.由于第三类舱室破损后存在自由液面的影响,两种破损船舶的最大复原力臂、稳性消失角,以及静稳性曲线下的面积相比于完整状态均减小,即船舶破损后的稳性比完整状态差,且不对称浸水船舶由于有较大的初始横倾角,其稳性要比对称浸水船舶的稳性更差.此外,破损船的有效波倾系数曲线比完整船略有下降,原因是船舶破损后对波浪的绕射效应相比完整状态有所减弱.

图5 复原力臂曲线和有效波倾系数曲线
编制程序模拟规则波中DTMB5415的单自由度横摇运动,并将时域横摇运动结果与实验结果进行比较,以验证程序的可靠性.计算与实验均不考虑风的影响,两者的波浪条件一致,波幅取为波长的1/100,以对称浸水形式的DTMB5415破损船(无舭龙骨)为例,模拟破损船在规则波中的横摇运动时历曲线见图6.

图6 规则波中横摇运动时历曲线
各波浪条件下数值模拟与实验[12-13]得到的横摇角幅值结果见表5.

表5 数值计算横摇角与实验结果比较
由表5可知:程序计算的横摇角幅值相对于实验结果的误差在可接受的范围内,说明程序计算具有可靠性.造成误差的主要原因是程序采用单自由度横摇运动模型,没有考虑多自由度运动的耦合作用.
3.3 随机横浪中船舶横摇运动模拟与分析
采用程序模拟随机横浪中船舶的时域横摇运动,以对称浸水、不对称浸水形式破损船(均带舭龙骨)在随机横浪(HS=3.5 m、9.5 m,TZ=8.5 s)中的横摇运动为例,运动时历见图7~8.

图7 随机横浪中破损船横摇运动时历(HS=3.5 m,TZ=8.5 s)

图8 随机横浪中破损船横摇运动时历(HS=9.5 m,TZ=8.5 s)
对于线性系统,若其输入为平稳高斯随机过程,则其输出仍为平稳高斯随机过程,而船舶大角度横摇时存在非线性,其输出将不再符合上述规律.统计两种随机横浪(HS分别为3.5,9.5 m,TZ均为8.5 s)时历曲线(时长为1 h)中的一系列波幅,以及相对应的DTMB5415(带舭龙骨)横摇运动时历曲线中的一系列横摇幅值(峰值与谷值之差),分别绘制波幅分布和横摇幅值分布直方图,见图9~10,直方图中实折线表示瑞利分布.

图9 波幅分布和横摇幅值分布直方图(HS=3.5 m,TZ=8.5 s)

图10 波幅分布和横摇幅值分布直方图(HS=9.5 m,TZ=8.5 s)
如果平稳随机过程的瞬时值服从高斯分布,则其幅值服从瑞利分布.两种随机横浪的幅值近似服从瑞利分布.当船舶在有义波高为3.5 m、过零周期为8.5 s的随机横浪中作横摇运动时,由于横摇角度较小,此时船舶的复原力矩与横倾角、阻尼力矩与横摇角速度近似成线性关系,船舶系统仍为线性系统,其横摇幅值也近似服从瑞利分布.当船舶在有义波高为9.5 m、过零周期为8.5 s的随机横浪中作大角度横摇运动时,由于船舶的复原力矩非线性和阻尼力矩非线性,此时船舶系统为非线性系统,输出具有非线性,因此其横摇响应不再服从高斯分布,横摇幅值不再服从瑞利分布,且船舶的横摇幅值分布会整体向右偏移.
3.4 随机横风横浪中船舶倾覆概率计算
瘫船状态DTMB5415在随机横风横浪联合作用下的部分横摇运动时历见图11,若在单次模拟时间内船舶横摇角度超过所定义的实际倾覆角度50°,则认为船舶已经发生倾覆.

图11 随机横风横浪中横摇运动时历(HS=9.5 m,TZ=8.5 s)
运用蒙特卡洛方法对完整状态和两种破损形式的DTMB5415(带舭龙骨)在多个海况中的瘫船倾覆概率进行计算,其结果见图12.
由图12可知:相同海况中DTMB5415完整船的倾覆概率最小,对称浸水形式的倾覆概率次之,不对称浸水形式的倾覆概率最大.当海浪的过零周期处于7.5 s附近时,此时海浪的谱峰周期处于10.56 s附近,海浪主成分波的谱峰周期接近船舶的横摇固有周期,船舶进入横摇的临界区域,产生十分严重的横摇,三者瘫船时的倾覆概率均迅速增加.而当海浪主成分波的周期远离船舶的横摇固有周期时,船舶发生大角度横摇的可能性迅速减小,此时船舶的瘫船倾覆概率较小.
DTMB5415瘫船倾覆概率随有义波高的变化趋势见图13,图中各海况的过零周期根据北大西洋海浪谱中各有义波高对应的最高出现频率的过零周期进行选择.由图13可知:当有义波高在8.5~12.5 m,随着有义波高的继续增大,三者瘫船时的倾覆概率均迅速增加.且在该有义波高范围内,相同海况中DTMB5415完整船的瘫船稳性最好,对称浸水形式的瘫船稳性次之,不对称浸水形式的瘫船稳性最差.

图13 瘫船状态DTMB5415倾覆概率随有义波高变化趋势
4 结 论
1) IMO第二代完整稳性中所推荐的池田法不适用于计算破损船的横摇阻尼系数,破损船的横摇阻尼系数应当通过模型实验或者CFD模拟以获得较为准确的结果.
2) 将数值计算得到的船舶在规则波中的横摇角幅值与实验结果进行对比,验证了单自由度数值计算方法的可靠性.
3) 通过统计随机横浪中完整船和破损船的横摇幅值,分析得出船舶在小角度横摇时,由于船舶的复原力矩与横摇角、阻尼力矩与横摇角速度近似成线性关系,其横摇幅值也近似服从瑞利分布.而当船舶发生大角度横摇时,由于复原力矩和阻尼力矩的非线性,船舶系统为非线性系统,其输出具有非线性,横摇幅值不再服从瑞利分布.
4) 相同海况中,两种破损形式的船舶相较于完整船舶更容易发生瘫船倾覆现象,且破损船舶不对称浸水形式比对称浸水形式更危险.处于瘫船状态的船舶在遭受谱峰周期与自身横摇固有周期相近的波浪作用时,船舶进入横摇的临界区域,产生十分严重的横摇,发生倾覆的风险显著增加.
在计算DTMB5415瘫船状态的倾覆概率过程中,文中对有效波倾系数的计算采用SDC 7-INF.2文件中的“等效船舶”方法进行估算,并对船舶破损区域进行了简化处理.在后续研究中,应采用实验方法确定有效波倾系数,以获得更准确的结果.同时,程序计算采用单自由度横摇运动模型以快速获得瘫船倾覆概率计算结果,并未考虑多自由度运动之间的耦合作用,其计算结果与实际结果之间存在误差,今后应采用多自由度运动模型以获得更接近船舶实际运动的结果.

