基于最优时间间隔的足式机器人足端轨迹规划*
辛玉红 章永年
(①金陵科技学院机电工程学院,江苏 南京 211169;②南京农业大学工学院,江苏 南京 210031)
足端轨迹直接影响足式机器人的运动平稳性[1-2],是国内外学者的研究热点。利用笛卡尔坐标表示的足端轨迹易于实现地面接触检查、避障等功能[3-4],因此目前足端轨迹规划研究主要集中在足端轨迹曲线对运动平稳性的影响。如Cho J等[5]考虑到地面对足端的支持力影响,对垂直地面方向的足端轨迹曲线进行了规划,提高了机身稳定性。Chae K G等[6]优化了gallop步态的腾空相轨迹,降低了运动能耗。王立鹏等[7-8]提出一种零冲击的足端轨迹规划改进算法,减小了换相时的地面冲击力。Gao M等[9]通过优化入地角和足端轨迹曲率来提高机器人运动性能。
进行足端轨迹规划时,一般在任务空间产生一系列满足足端速度、加速度等约束条件的等时间间隔的离散数据点(任务空间),再进行运动学反解后得到各关节电机角度(关节空间),发送给各关节驱动器,使其按照要求运动。然而,足式机器人任务空间和关节空间存在非线性映射关系[10],仅仅在任务空间内规划得到的轨迹可能会导致机器人关节运动不平稳,但目前的足端轨迹规划算法基本没有考虑到这个问题。
实际上,在工业机器人的轨迹规划中也存在类似的问题。一般地,研究人员将任务空间轨迹离散为若干离散点,再在关节空间内规划出过这些点的关节运动平稳的轨迹。如Gasparetto A等[11]在考虑运动学限制的前提下,采用五次B样条曲线进行规划,进而采用优化算法得到加工时间和加加速度加权和最小[12-13]的目标轨迹。Liu H等[14]、Olabi A等[15]和Alatartsev S等[16]对关节空间的运动平稳性进行了优化,但牺牲了离散点间的运动精度。这种轨迹规划算法适用于对轨迹精度要求不高的情况。
考虑到任务空间内足端轨迹曲线对运动性能的影响,本文在保证任务空间离散点轨迹不变的前提下,分析任务空间和关节空间速度间的非线性映射关系,对已经规划好的离散点所对应的时间间隔进行重新规划,构建机器人关节空间、任务空间运动性能指标与离散点时间间隔的关系,利用改进的遗传算法获取最优的时间间隔,使其满足兼具任务空间、关节空间的平稳性运动要求。
1 机器人模型分析
本文中所采用的机器人(如图1所示)为内膝肘式,机器人的4条腿具有相同的机械结构,每条腿具有3个关节,每个关节由1个直流伺服电机控制。
对于图1所示的机器人三段式腿部结构,有研究表明人及大型的四足动物腿部结构中大腿、小腿和足部的腿节比例为0.39∶0.45∶0.16,小型哺乳类动物常见的腿节比例为0.33∶0.33∶0.33,这样的构形配置可以为它们带来较大的工作空间及较好的加速性能。因此本文也采用这样的腿节比例,具体的尺寸参数如表1所示。

图1 四足机器人三维模型

表1 机器人单腿结构参数

式中:J为速度雅克比矩阵,由下式确定。
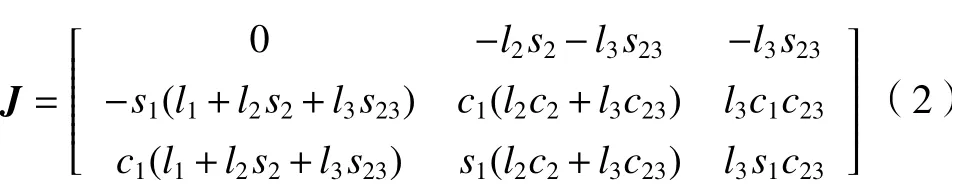
由于任务空间与关节空间的存在非线性的速度映射关系,因此仅在任务空间内进行足端规划可能会导致关节电机的速度、加速度超限或发生突变,影响机器人的运动平稳性。
2 机器人足端轨迹的多目标优化算法
与单目标优化问题一样,多目标优化问题包括目标函数,决策变量和约束条件[17],其一般结构如下
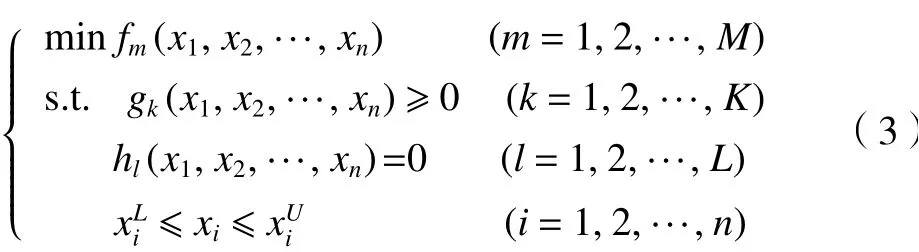
式中:X⊂Rn为 决策空间,集合显然可行为变量上下界。同时该多目标问题的可行域域 Ω⊆X。
2.1 设计变量
由于机器人控制器产生步态轨迹离散点的方法各异,为了保持本文算法的普适性,在这里不改变已经离散好的轨迹点Pi,只是更改离散轨迹点之间的时间间隔 Δti,从而对各关节速度、加速度进行调整。因此,该机器人轨迹规划的多目标问题的设计量为x=(Δt1,Δt2,···,Δtn), 其中n为1个步态周期内足端轨迹的离散点个数。
2.2 约束条件
(1)步频约束
优化前后机器人的运动速度保持不变,记T为机器人步态周期,有

(2)任务空间运动学约束
足式机器人在任务空间的运动平稳性会影响机器人与地面的接触力,因而足端轨迹在任务空间也必须保持平稳运动,有

式中:vi、ai分 别为第i个足端轨迹点的速度、加速度,vmax、amax为其许用的最大速度、加速度。
(3)关节空间运动学约束
每个关节均受到关节最大速度、加速度、加加速度的限制,即

式 中:Vk,i、Ak,i、Jk,i分 别 代 表 第k个 关 节 在 第i个 足端轨迹点的速度、加速度及加加速度,Vk、Ak、Jk代表第k个关节许用的最大速度、加速度及加加速度。
2.3 目标函数
无论在关节空间还是任务空间,机器人的运动都应具备良好的运动平稳性。对运动平稳性的衡量可以表征为速度、加速度变化小,也就是系统具有较小的平均加速度和较小的平均加加速度。于是机器人任务空间的平稳性能子目标函数为
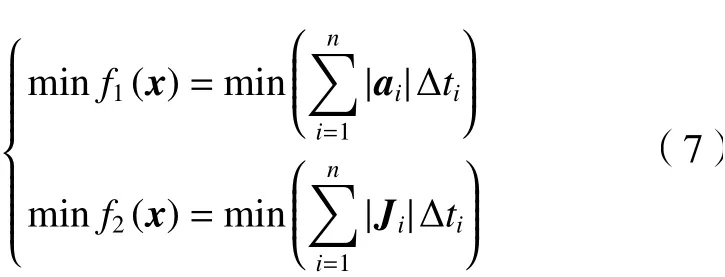
每个机器人关节的关节空间平稳性性能子目标函数为
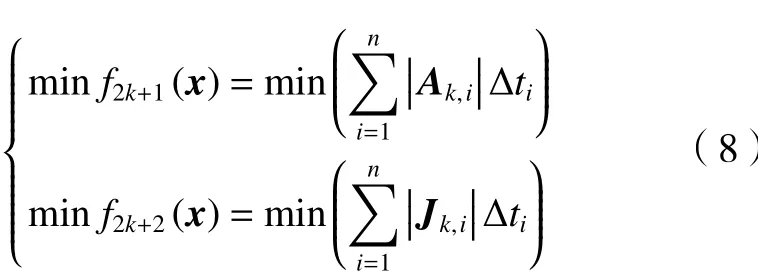
单腿含有3个关节,因此关节空间平稳性性能子目标函数一共有6个。基于上述的约束条件和子目标函数的分析,建立足端轨迹的多目标优化模型
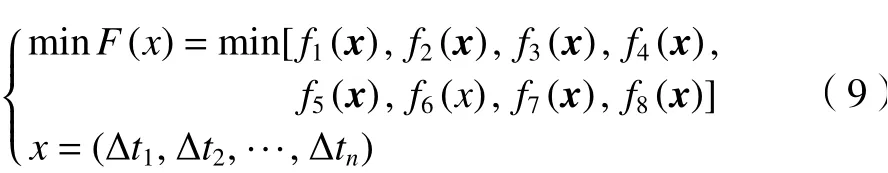
3 遗传算法
3.1 归一化处理
首先对各个独立的分目标函数求最大值和最小值,再将实际的目标函数转换为0~1之间的一个无量纲数。即

为了将不同的性能因素在目标衡量中的相对重要程度定量化,设Wm为几种性能指标的权比,该值采用层次分析法计算得到,这样统一的目标函数为
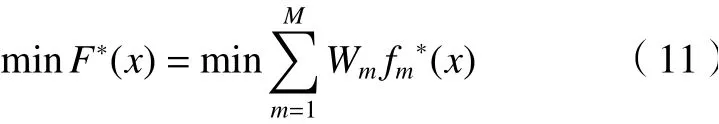
3.2 改进遗传算法
待优化单目标函数式(11)是一个非线性优化问题,运用标准优化算法很难解决,这里采用改进遗传算法来求解。其算法流程图如图2所示。

图2 GA流程图
与常规染色体变异[18]不同,本文对单个染色体上多个基因组进行变异。具体过程如下:
(1)基因组划分
本文的染色体由 Δti按序排列而成,如图3所示。

图3 单个染色体
当轨迹点Pi运动学参数不满足任务空间运动学约束或关节空间运动学约束时,该点即为染色体上基因组分割点,据此划分得到基因组如图4所示。

图4 基因组划分图
(2)变异过程
完成基因分组后,在轨迹点不变的情况下,增大某轨迹点Pi附近的时间长度可以降低关节空间速度、加速度、加加速度和足端速度、加速度的大小及突变程度。但若只对Pi点附近的时间长度作调整,可能会导致附近其他轨迹点出现峰值,使得优化效果有限,甚至更差。故而将调整目标扩展到基因组。将该基因组进行整体缩放,同时乘以染色体片段突变 系 数Ci, 实 现 增 大 Δti的 目 的。
4 试验结果与分析
试验用四足机器人样机如图5所示,驱动装置选用Maxon的RE35直流有刷电机及LT1100直流伺服驱动器。

图5 机器人样机
机器人行走时应该尽量满足行走平稳、关节冲击小、跨步迅速和轨迹圆滑等要求,因此足端轨迹选用北京理工大学提出的一种零冲击足端轨迹[7],步态采用速度快、稳定性好的对角步态。设置步距100 mm,步高40 mm,步态周期4 s,离散点总数为100,得到图6所示的待优化的离散点序列Pi。足端轨迹位于xy平面内,相邻2个离散点之间的时间间隔均为0.04 s。
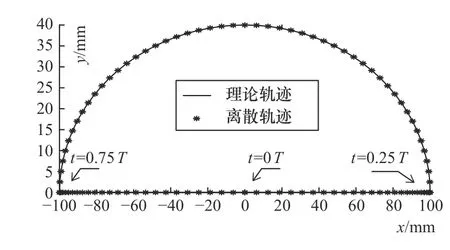
图6 四足机器人椭圆足端轨迹
利用改进的遗传算法对离散点序列进行轨迹优化,其算法参数如表2所示。

表2 算法参数
由于足端轨迹在Z方向没有变化,因而优化前后横摆关节的角度保持不变。将优化前后的各关节PVT信息发送至驱动器,得到实物样机髋、膝关节速度、加速度和加加速度的情况如图7所示。
从图7可以看出,优化前的足端轨迹在1 s、3 s附近时速度、加速度和加加速度均有不同程度的突变,此时足端轨迹位于支撑相与腾空相的转换之中,由于整个足端轨迹曲线在支撑相与腾空相转换的位置处仅为C1连续,因而在进行轨迹规划时容易在此处发生速度突变,影响运动的平稳性。

图7 优化前后关节空间性能对比图
优化后的速度曲线比优化前的速度曲线更加平滑,换相点处的速度突变现象也得到了很大的改善。优化后的加速度、加加速度峰值均不同程度的降低,提高了运动的平稳性,具体的性能指标如表3所示。
从表3可以看出,无论是腾空相还是支撑相,髋关节和膝关节的峰值加速度和峰值加加速度都比优化前有所下降,最高降幅达77.15%,最低降幅也有37.22%。另外除了膝关节的平均加速度较原来提高10.89%外,髋关节的平均加速度、两个关节的平均加加速度均比优化前有所下降。从而可以表明优化后关节空间的运动平稳性能得到大幅提升。

表3 优化前后性能对比
足式机器人在任务空间的运动平稳性会影响机器人与地面的接触力,因而在提高关节空间的运动平稳性能同时,其任务空间的运动平稳性也应基本保持不变甚至有所提升。图8给出了优化前后任务空间的加速度对比。
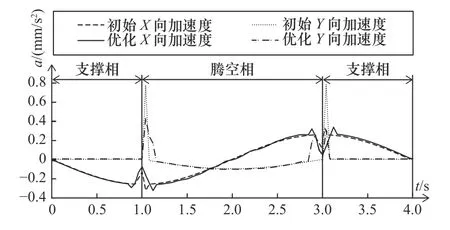
图8 优化前后任务空间性能对比图
从图8可以看出,优化前后X向的加速度曲线变化不大,可以看出本文提出的遗传算法由于采用了分段染色体变异的策略使得能选择性保留原有比较优秀的加速度曲线。而优化前Y向在换相点处存在较大的加速度突变,经过优化后,在1 s、3 s时刻最大冲击分别减小了45.83%和61.82%,由于机器在行走过程中,Y方向上的冲击是机身造成翻转和倾覆的主要影响因素,因而能大大减小行走冲击,提高机器人行走的稳定性。
5 结语
本文提出了一种优化四足机器人足端轨迹的新方法。在不改变已经离散好的轨迹点的前提下,在关节空间、任务空间运动学约束条件下,以任务空间和每个机器人关节的关节空间平稳性性能为评价指标,利用遗传算法优化轨迹点之间的时间间隔使得评价指标达到最优。试验结果显示:
(1)机器人各关节的峰值加速度、峰值加加速度都比优化前有所下降,表明关节电机受到较小冲击。
(2) 除膝关节的平均加速度较原来提高外,髋关节的平均加速度、2个关节的平均加加速度均比优化前有所下降,表明关节电机的运动平稳性得到提升。
(3) 竖直方向在换相点处加速度比优化前有所下降,减小了行走冲击,提高机器人行走的稳定性。

