基于Levenberg Marquardt 的数控机床主轴负载振动的非线性拟合
林海森 邹朝圣 廖妮兰 廖城鸿
(厦门万久科技股份有限公司,福建 厦门 361021)
生产制造,从早期的人工、机械、半自动化和自动化,到信息化、数字化,再到现在的智能制造,其发展趋势已势不可挡,而且智能制造也是全球制造业发展的趋势[1]。智能制造离不开数控机床,在我国“智能制造2025”的环境下,数控机床主轴振动信号的采集、监控与分析已经成为了行业热议的话题。如苏健[2]等提出基于三次样条函数的 FFT 优化算法,研究了机床主轴的振动信号;万海波[3]等基于 HHT 的主轴振动信号,实时监测振动信号的时频分布;董鑫[4]等利用谱图小波阈值降噪、逆变换,分析了滚刀主轴振动信号。研究数控机床主轴振动量,将数据可视化对于智能化生产与管理具有十分重要的意义。
数控机床加工时,其主轴振动量与主轴转速、进给速度和切削量这3个变量因素息息相关,而三者与主轴振动量是非线性关系,寻求关系函数需求解非线性方程。当前求解非线性方程组最常用的经典方法为牛顿法(Newton)方法,高斯牛顿法(Gauss-Newton)方法,列文伯格-马夸尔(Levenberg-Marquardt,L-M)方法等,其中L-M算法介于牛顿法与梯度下降法之间的一种非线性优化方法,具有梯度法和牛顿法的优点[5-6]。
L-M算法与最小二乘方法关系密切,能有效解决多元非线性曲线拟合,估算函数的未知参数,在工程应用中很有实用价值。其使用信赖域,修正阻尼因子u,当u很小时,步长取牛顿法(Newton)的最优步长,当u很大时,步长取梯度下降法(Gradient Descent)的最优步长,得到合适的值,在迭代更新过程使方程有效收敛,最终达到求解结果[6-7]。
本文使用三维度的速度传感器(VB-300)分别收集数控机床主轴负载时的振动速度量与主轴转速、进给速度和切削量3个因素的关系数据,以L-M算法为基础,进行多元非线性曲线拟合求得最终关系函数,实现数控机床主轴负载时振动量的估测,以及对加工过程中出现异常的报警。
1 检测系统方案设计
本文选取速度传感器(VB-300),具有三维度的速度检测,用于采集机床主轴振动信号,速度传感器安装于机床主轴右侧,不影响加工,其整体布局效果如图1所示,系统框架图如图2所示。

图1 速度传感器布置
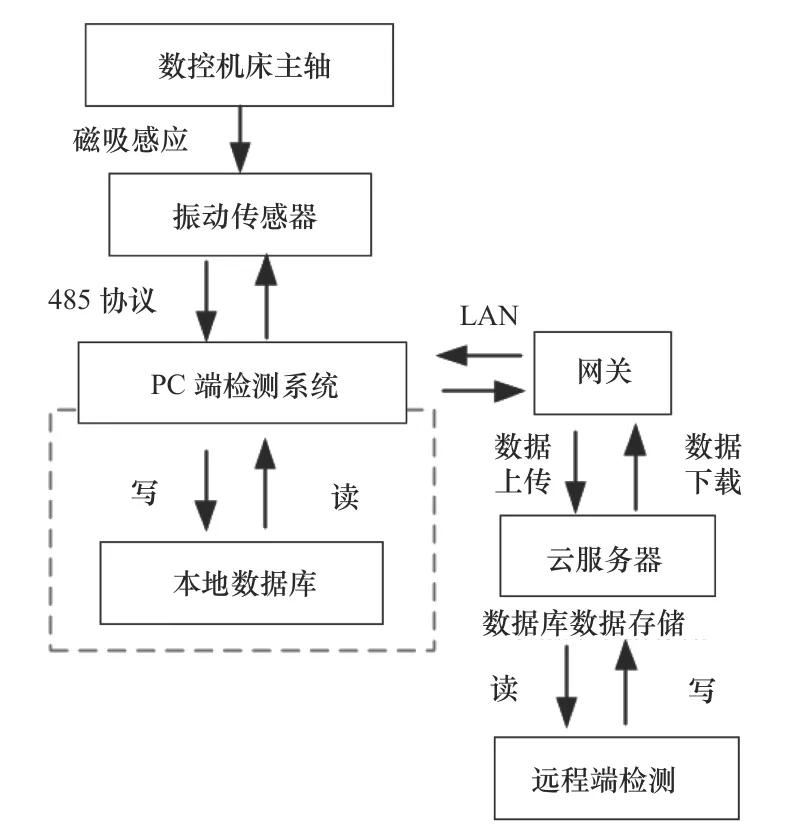
图2 系统框架图
2 多元非线性拟合
2.1 主轴振动与因变量关系
数控机床主轴负载时,其振动幅度与主轴转速x1、进给速度x2、切削量x3的变量因素相关,当变量因素都不变的情况下,加工过程中随着时间t的变化,主轴在3个方向的振动值Y在应许的容差内波动,呈现水平分布,如图3所示。

图3 主轴振动与时间关系图
为了便于推算拟合的函数关系式,根据主轴负载时的振动数据,分别取3组数据进行拟合,可得数控机床的主轴转速x1、进给速度x2、切削量x3与主轴振动幅度关系分别呈现指数函数关系(y=eAx+B)。同时,考虑拟合效果,主轴转速数值缩小1 000倍进行拟合,即取7.2~9.6 r/min,其曲线分布如图4~6所示。
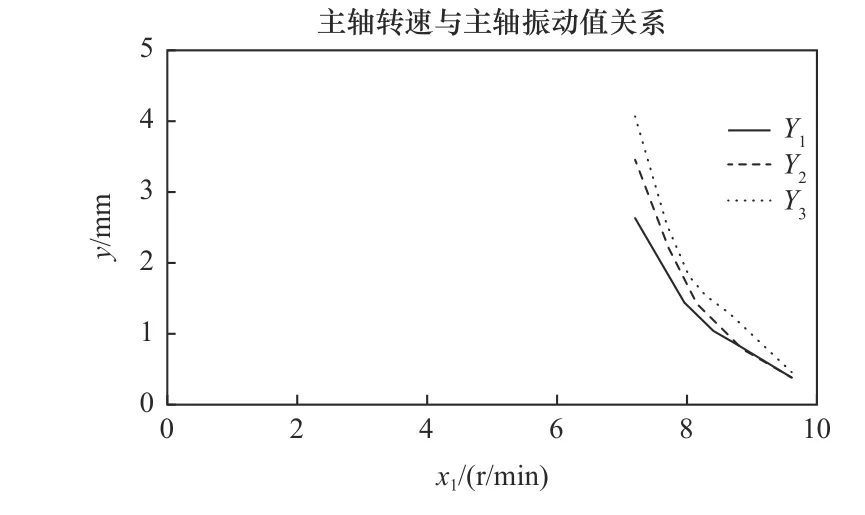
图4 主轴转速与主轴振动值关系图
2.2 基于L-M的多元非线性曲线拟合
本文基于L-M算法,分析了机床主轴负载时的振动与主轴转速x1、进给速度x2和切削量x3三者的关系,估测主轴的速度振动值。确立初始函数关系的主流程,如图7所示。
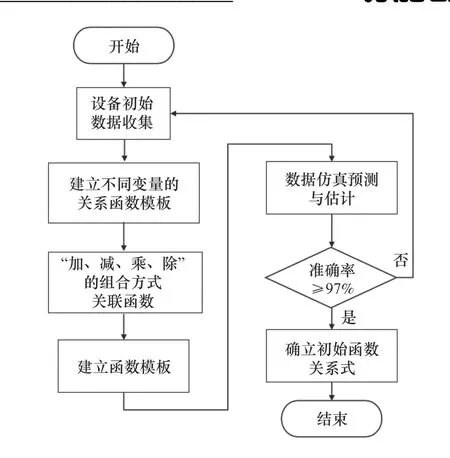
图7 确立函数关系式流程图

图5 进给速度与主轴振动值关系图

图6 切削量与主轴振动值关系图
多元非线性曲线拟合实现过程如下:
(1)求取参数 β=(β1,β2,β3,β4,β5)的初始函数Yi=f(Xi,β),结合上述2.1内容中确定的不同变量的关系函数模板,进行“加、减、乘、除”方式组合,
确立初始函数关系式为
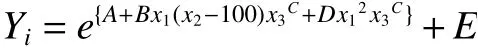
以下以Yi=f(Xi,β)进行表示计算。
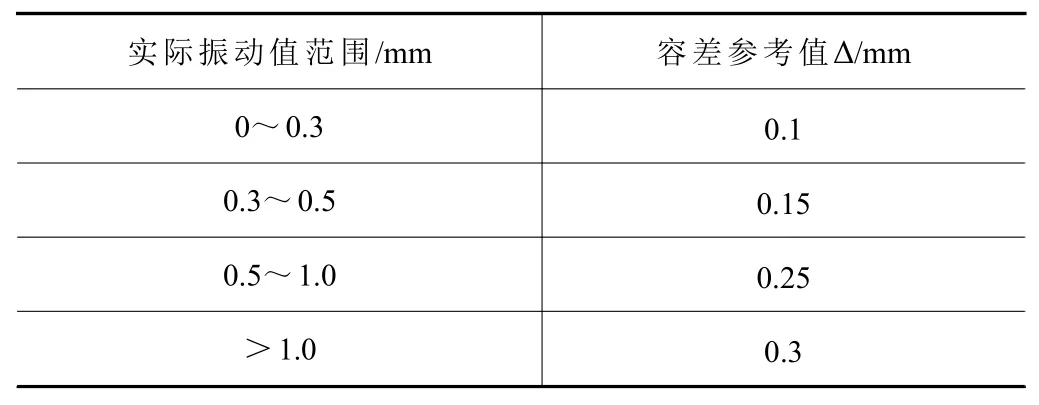
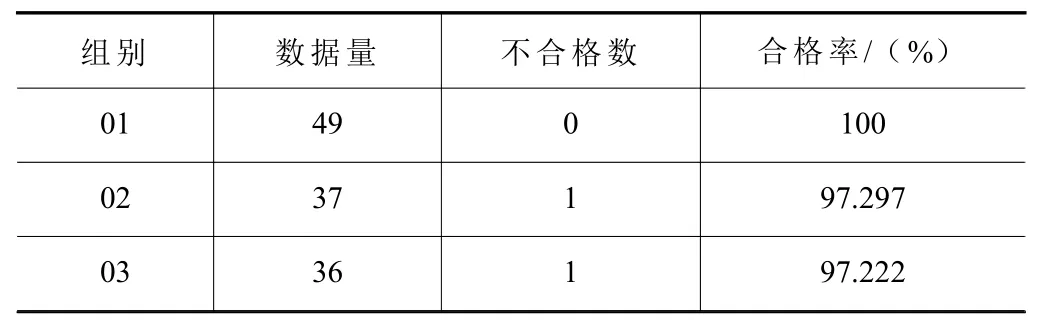
(2)初始给定一组数量为m的经验数据(Xi,Yi),0 (3)求取最优参数β,可由偏差ri(β)的 平方S(β)和最小求得,用最小二乘法方式表示有 (4)由于雅克比矩阵 根据一阶泰勒展开有 结合式(1)有 (5)L-M算法使用了一种带阻尼的高斯-牛顿方法,式(2)引入阻尼项,有 其中:I为单位矩阵,正阻尼因子ui=||ri(βk)||2全局收敛[8],0 (6)求偏差的最小值,则对式(3)求偏导,并令为0,则有 (7)若 ||gi(βk)||∞≤ε1则退出迭代,否则继续,常数值 ε1=10-15。 (8)若 | |Δβ||2≤ε2(||βk||2+ε2),则退出迭代,否则继续,常数值ε2=10-15。 (9)更新 βk+1=βk+Δβk。 (10)计算增益比 (12)重复(6)到(11)的步骤,直至迭代结束。 本文通过拟合的曲线进行估测主轴的振动值,与实际值比较,当超过应许的容差时,判断为异常,主轴停止并报警处理,保证机床加工的稳定性。实现异常报警的程序流程图,如图8所示,其中n1为每组数据的数量、n2为数据异常的数量。 图8 异常判断流程图 根据上述步骤,拟合曲线方程为确立初始函数关系式为 本文相关测试设备组成如表1所示,其测量的振动值对应的容差参考值如表2所示,其他变量条件: 表1 主要设备 表2 容差参考表 主轴转速7 200 r/min≤x1≤9 600 r/min;进给速度100 mm/s≤x2≤ 400 mm/s;切削量0.1 mm≤x3≤0.5 mm。 随机选取3组数据进行估测比较,其实验结果如表3所示。 表3 实验数据表 综上所述,在数控机床主轴负载时,有: (1)主轴转速间隔800取一组,共4组;进给速度间隔100取一组,共4组;切削量间隔0.1取一组,共5组。三者之间自由组合,共80组,保证数据的可靠性。 (2)容差值与主轴振动幅度值正相关,可减少误差放大,提高数据估测的准确性。 (3)随机性抽取多组数据验证,合格率超过97%,保证数据估测的有效性。 因此,本文所述算法能很好地拟合估测主轴振动量与主轴转速、进给速度和切削量三者的关系,保证数控机床加工的稳定性。 本文基于Levenberg Marquardt算法,多元非线性拟合,确立主轴转速、进给速度和切削量三者与机床主轴速度振动量的函数关系。在数控机床加工中,实时监测主轴振动状态,判断主轴是否异常和刀具是否断裂,保证数控机床加工的稳定性,提高生产效率。实验结果表明,该方式能有效地预估主轴的速度振动量,准确率超过97%。同时,对于后续数控机床主轴的平衡性、撞击和刀具寿命管理等有很大的参考价值。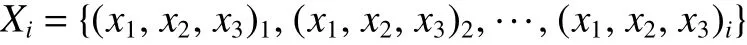







2.3 异常报警监测

3 实验结果
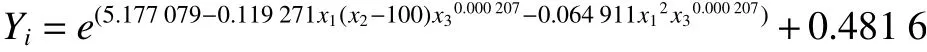

4 结语

