采用扩展滑模观测器的数控机床永磁同步电机鲁棒控制方法＊

李 涛

（郑州旅游职业学院，河南 郑州 451464）

永磁同步电机在数控机床加工领域有着广泛的应用，尤其在高端制造业方面对永磁同步电机的运行精度有着更高的要求[1-3]。由于永磁同步电机是依靠电路和磁路来工作的，电源的稳定性和外界温度变化也都会影响电路的稳定[4-5]，同时外界磁场的变化也会影响磁路的稳定[6-7]，进而破坏永磁同步电机电流和磁链的稳定，最终干扰电机的正常转动。另外，由于负载转矩是时刻变化的，无法获得负载转矩的准确信息，那么未知负载转矩扰动也必然会影响到控制转速的精度[8-9]。

文献[10]采用无模型预测控制器设计了永磁同步电机鲁棒调速方法，但是没有考虑未知负载转矩的影响；文献[11]通过建立永磁同步直线电机增量式预测模型来克服电机磁链变化的影响，并利用滑模观测器来观测电压扰动值并将扰动前馈补偿，设计了鲁棒增量式预测电流控制算法，虽然方法有效，但是没有考虑未知负载力矩的影响；文献[12]利用自适应估计法对不确定因素在线估计，设计了模糊滑模控制算法，但没有考虑未知负载转矩的影响；文献[13]采用鲁棒微分估计器设计了平滑非奇异终端SMC算法，大幅改善了系统的稳定性，但没有考虑鲁棒控制问题；文献[14]针对存在模型参数非线性不确定性因素和输入饱和约束的永磁同步电机控制问题，设计了干扰观测器实现对不确定性因素的在线估计和前馈补偿，设计了具有抗输入饱和约束的鲁棒有限时间控制算法，取得了不错的效果。综合以上分析，本文针对考虑负载转矩扰动和电路、磁路扰动的永磁同步电机转速控制问题，利用扩展滑模观测器来准确估计电机转速、转动加速度和复合干扰，给出了一种改进的鲁棒控制策略，大幅度提高了转速的精准度。

1 模型建立

永磁同步电机的结构较为简单，由定子、转子和壳体组成。示意图如图1所示。

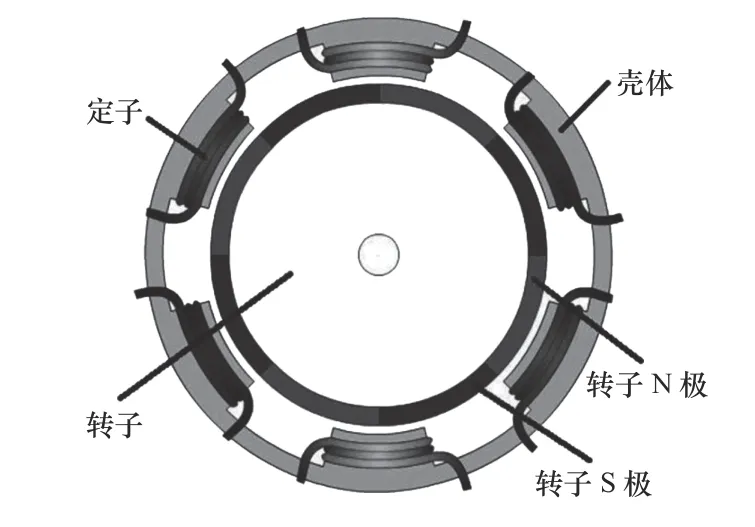
图1 永磁同步电机示意图

永磁同步电机的转动模型可以描述为：

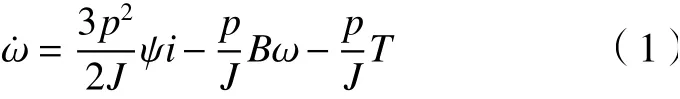
式中：ω表示转子转动角速度；p表示磁极对数；J表示转动惯量；ψ表永磁磁链；i表示输入电流，即输入控制指令；B表示摩擦系数；T表示额定负载转矩[15]。

数控机床在对工件加工的过程中，永磁同步电机负载转矩是时刻变化的，无法准确获得负载转矩的大小，所以一定要考虑未知负载转矩的影响。另外，永磁同步电机的电路和磁路也容易受到外界电磁场的影响，使电机中的电流大小和磁链大小会发生不规则扰动，必然会影响转子转速的精确。

综合考虑负载转矩扰动和电路、磁路扰动的影响，建立永磁同步电机的转动模型可以描述如下。

式中：r为负载转矩扰动和电路扰动的复合干扰。

2 鲁棒控制律设计

首先设计了扩展滑模观测器对复合干扰和转速进行估计，并分析了扩展滑模观测器的稳定性以及对抖振现象的抑制作用；然后在此基础上，又设计了新型滑模趋近律，最终提出了鲁棒控制方法。控制系统结构如图2所示。

图2 控制系统结构

2.1 扩展滑模观测器设计

由于永磁同步电机转速非常快，传感器不能准确测量得到转速，将会影响对转速的精确控制，为了解决这个问题，设计了扩展滑模观测器来准确估计转速，并对复合干扰进行补偿。根据永磁同步电机的转动模型，将复合干扰r作为系统扩展状态变量，则可得到永磁同步电机的扩展动态模型为：

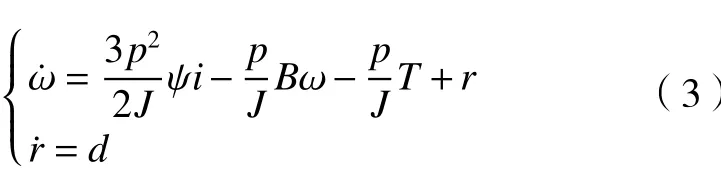
式中：d为永磁同步电机复合干扰r的变化率。

为式（3）设计扩展滑模观测器为

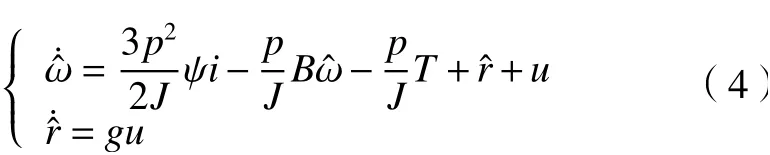
式中： η＜0是 滑模系数；sgn()是 符号函数；S是滑模面，表达式为

结合式（3）和式（4）得到扩展动态误差模型描述为

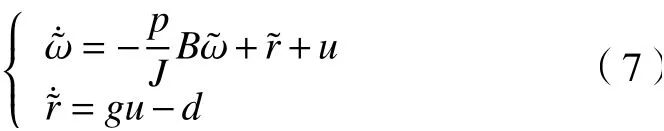
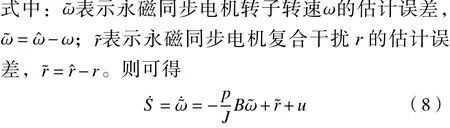
定理1：针对永磁同步电机的转动模型式（2）设计的扩展滑模观测器式（4）收敛。

证明：当以下条件成立时，扩展滑模观测器式（4）收敛，滑模面式（6）能够到达稳定状态：

将式（8）代入式（9）化简可得

将式（11）代入式（7）可得

由式（12）得到复合干扰r的误差微分方程：

对上式微分方程求解可以得到：

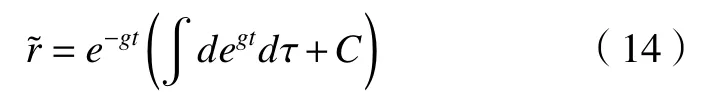
式中：C为常数。由式（14）可得到，当控制系数g＞0时，可确保复合干扰r的估计误差指数收敛到0，g的取值大小直接决定估计误差r˜的收敛速度。

定理2：设计的扩展滑模观测器式（4）可抑制高频抖振。

证明：在扩展滑模观测器中，抖振现象是由滑模变量u带来的。永磁同步电机的扩展动态误差模型可以重新描述为

进一步可得到滑模变量u的误差微分方程为

对式（16）进行拉普拉斯变换可得到

式中：T=1/g；F(s)为惯性环节，可以作为低通滤波器，能够有效抑制高频抖振现象，其中低通滤波器的截止频率为

综合以上分析，可得定理2成立，即扩展滑模观测器式（4）能够有效抑制抖振现象。

2.2 新型滑模鲁棒控制律设计

定义永磁同步电机转速误差为

式中： ωc为永磁同步电机的转速指令。选取滑模面为

对滑模面式（20）求导可以得到

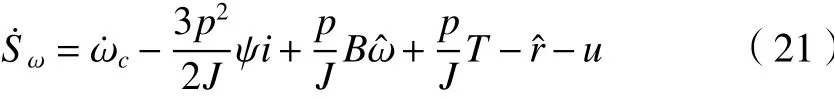
为了提高系统的收敛速度，克服滑模控制的抖振现象，本文设计新型滑模趋近律为

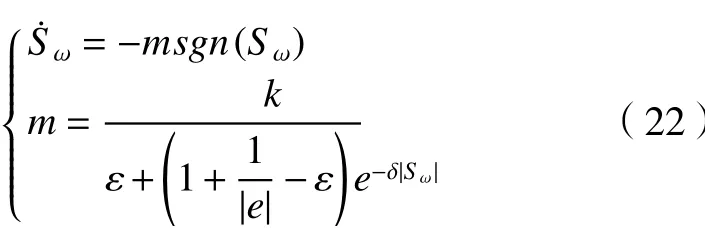
式中：k＞0； δ＞0； 0＜ε＜1；m是新型滑模趋近律的调节系数，来改善滑模控制的收敛速度和抖振现象，调节系数m满 足 0＜m＜k/ε。

设计的新型滑模趋近律工作原理为：当滑模面|Sω|增大时，即系统状态远离滑模面时，m趋近于常数k/ε， 且k/ε＞k，从而提高了系统的收敛速度；当滑模面 |Sω|减小时，即系统状态趋近滑模面时，m逐渐趋近于 (k|e|)/(1+|e|)。同时，在滑模控制的作用下，系统状态会逐渐收敛到0，则m会逐渐减小到0来抑制抖振。

将新型趋近律式（22）代入式（21）可得到

对式（23）进行求解可得到永磁同步电机输入电流的控制指令为

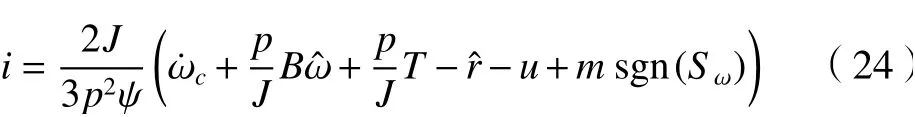
式中：复合干扰r由扩展滑模观测器式（4）估计得到；m满足式（22）。进一步可得到永磁同步电机输入电流的控制指令为

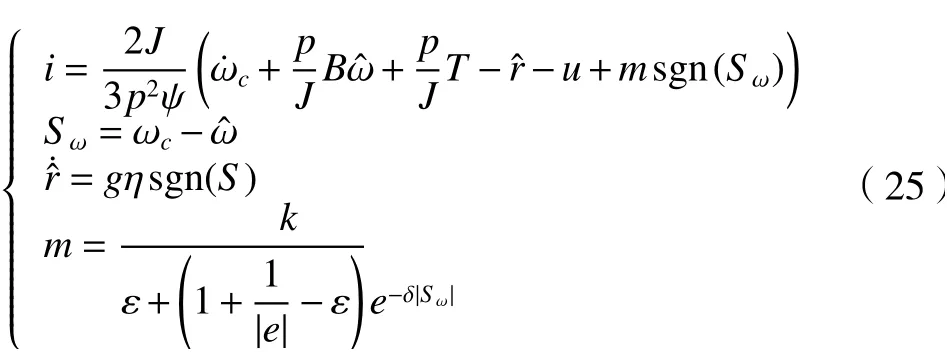
定理3：针对数控机床永磁同步电机的转动模型式（2），设计的新型滑模趋近律式（22）和输入电流控制指令式（25）能够保证系统稳定。

证明：考虑如下Lyapunov函数V

对式（26）求导并把式（22）和式（25）代入化简得

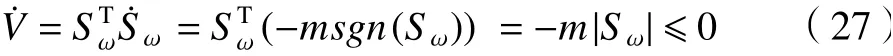
由Lyapunov稳定性定理可得到定理3成立，即设计的新型滑模趋近律式（22）和输入电流控制指令式（25）能够确保永磁同步电机系统稳定。

3 仿真验证

3.1 仿真参数设置

永磁同步电机的参数如表1所示。

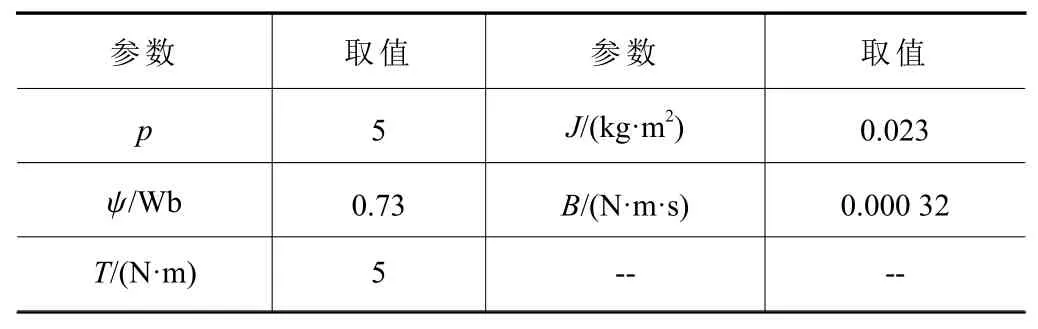
表1 永磁同步电机参数

设置永磁同步电机的初始状态为

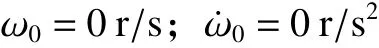
设定永磁同步电机的转速指令信号为

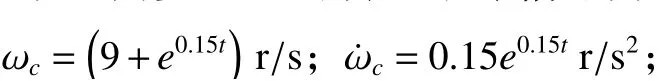
设定复合干扰为

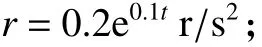
设置鲁棒控制律参数如表2所示。

表2 鲁棒控制律参数

3.2 转速对比

为了验证本文设计方法的优越性，分别采用文献[16]的滑模控制方法与本文方法进行转速对比仿真，得到的结果如图3所示，图3a为转速指令跟踪曲线，图3b为转速跟踪误差曲线。其中，实线为指令信号，短虚线为文献[16]的仿真曲线，长虚线为本文方法的仿真曲线。

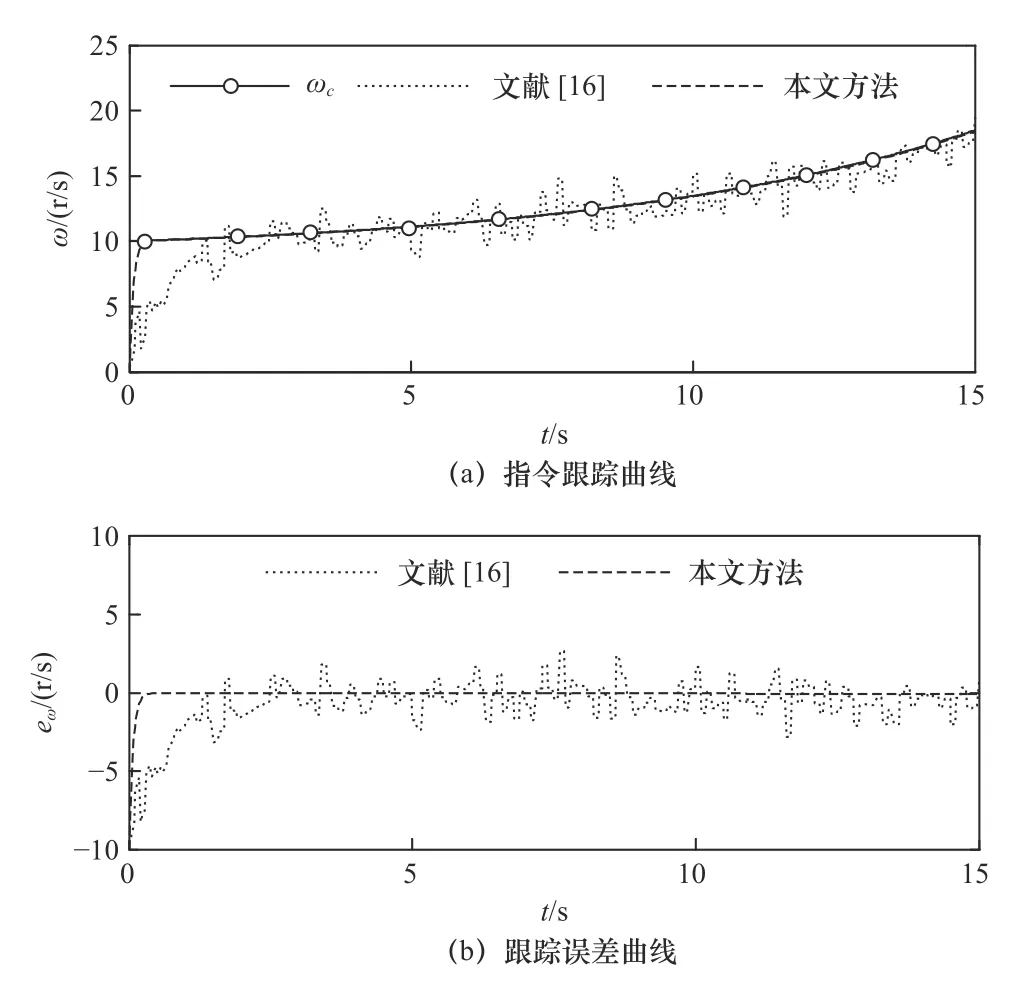
图3 转速仿真结果

由图3可看出：在文献[16]控制方法能够使永磁同步电机的转速在2 s之后才能基本跟上指令信号，但是在复合干扰的影响下，跟踪曲线会在指令信号附近剧烈振荡，最大跟踪误差达到了3 r/s；而在本文提出的控制方法作用下，转速在0.4 s内就可以稳定、准确跟踪指令信号，最大跟踪误差仅为0.1 r/s。

3.3 转动加速度对比

采用文献[16]的滑模控制方法和本文方法进行转动加速度对比仿真，结果如图4所示，图4a为转速指令跟踪曲线，图4b为转速跟踪误差曲线。其中，实线为指令信号，短虚线为文献[16]的仿真曲线，长虚线为本文方法的仿真曲线。

由图4可看出：在文献[16]控制方法能够使永磁同步电机的转动加速度能够基本跟上指令信号，但是在复合干扰的影响下，跟踪曲线会在指令信号附近剧烈振荡，最大跟踪误差达到了2 r/s2；而在本文提出的控制方法作用下，转动加速度能够迅速、准确跟踪指令信号，最大跟踪误差仅为0.05 r/s2。

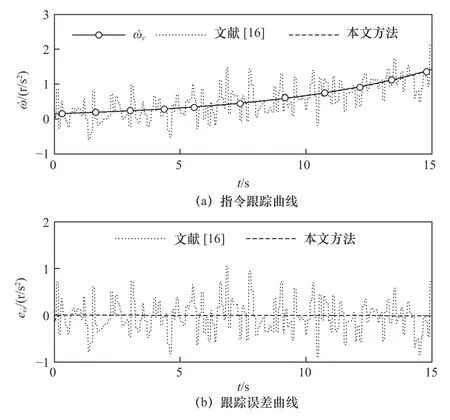
图4 转动加速度仿真结果

3.4 扩展滑模观测器对比

采用文献[17]的滑模观测器和本文方法进行对比仿真，得到转动速度估计结果、转动加速度估计结果和复合干扰估计结果，如图5～7所示。

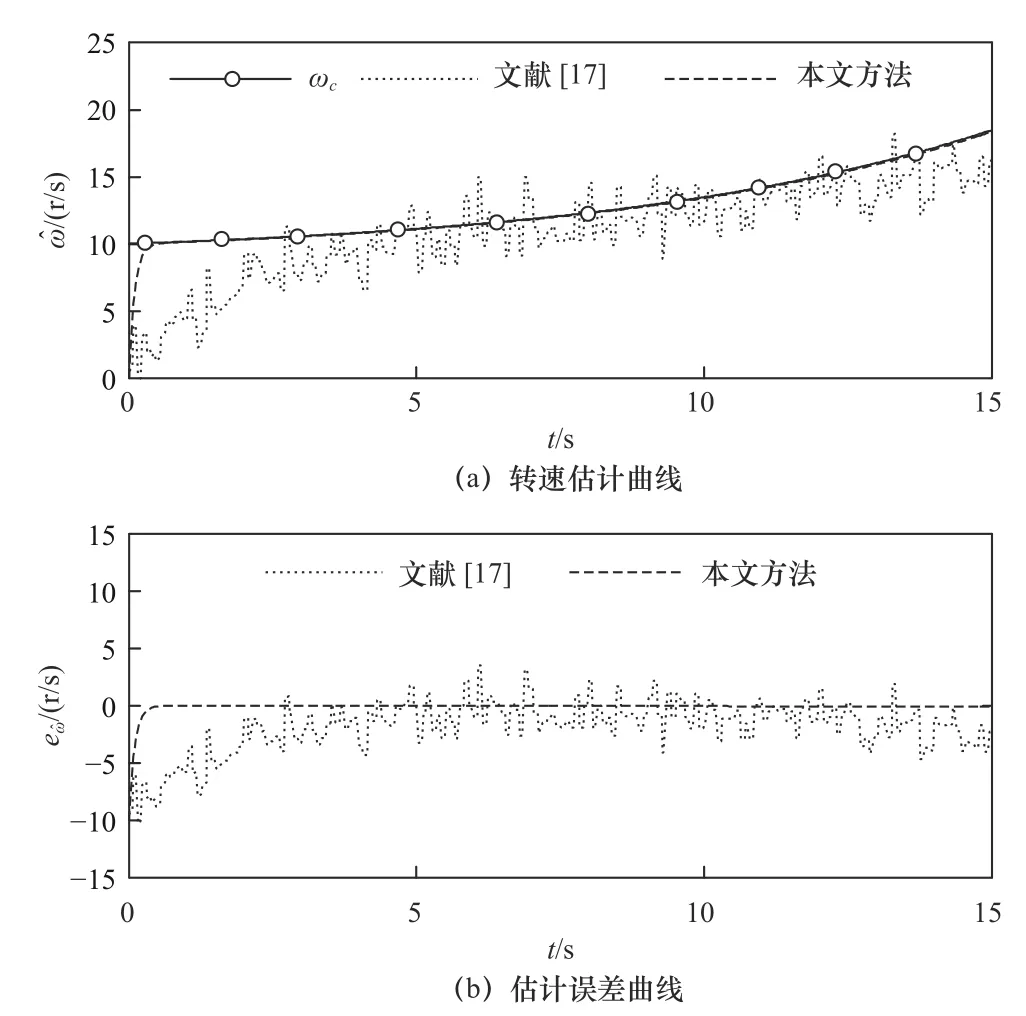
图5 转动速度估计结果

由仿真图5～7可看出：在文献[17]中的滑模观测器可使转速估计值在3 s之后基本跟上真实值，最大估计误差为4 r/s，转动加速度也能够基本跟上真实值，最大估计误差为2 r/s2；而在本文设计的扩展滑模观测器的作用下，转速估计值在0.4 s内就可以稳定、准确估计真实值，最大估计误差仅为0.08 r/s；转动加速度能够迅速、准确估计真实值，最大估计误差也仅为0.04 r/s2。另外，设计扩展滑模观测器可在0.4 s内准确估计出复合干扰，最大估计误差为0.03 r/s2。

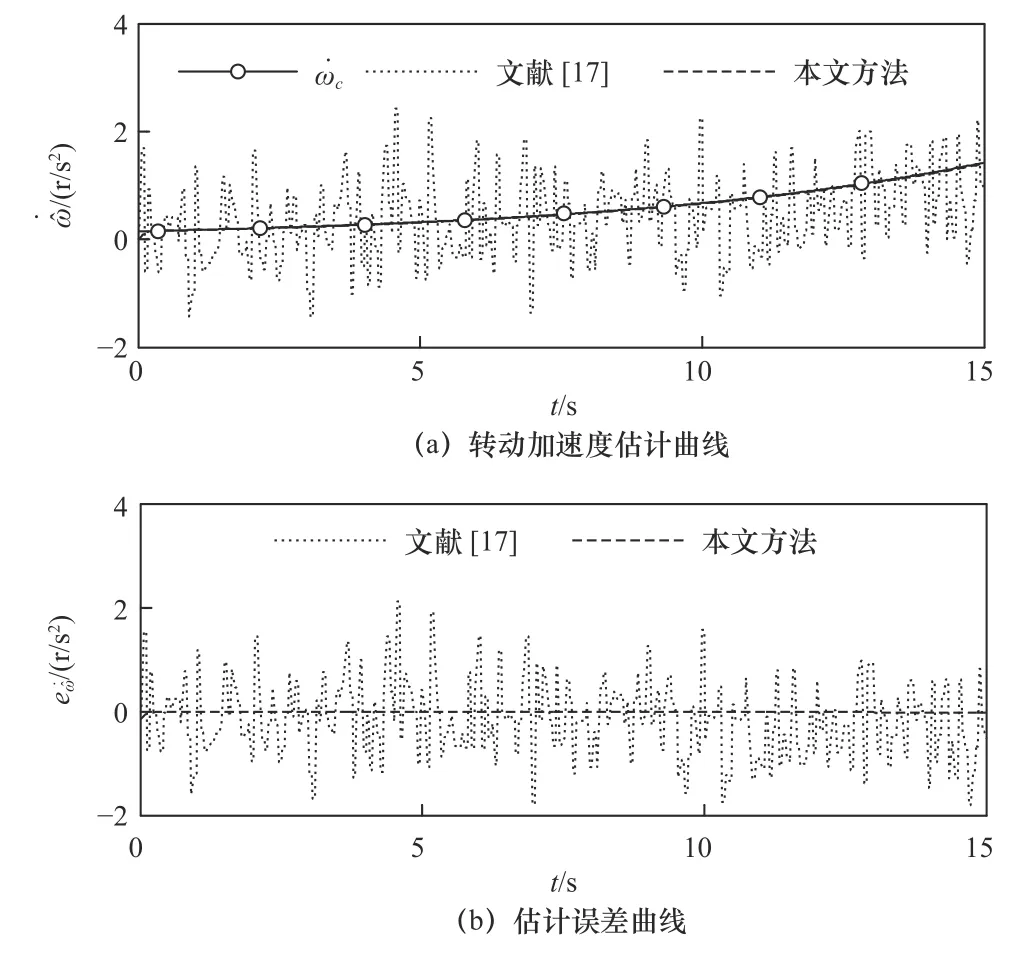
图6 转动加速度估计结果

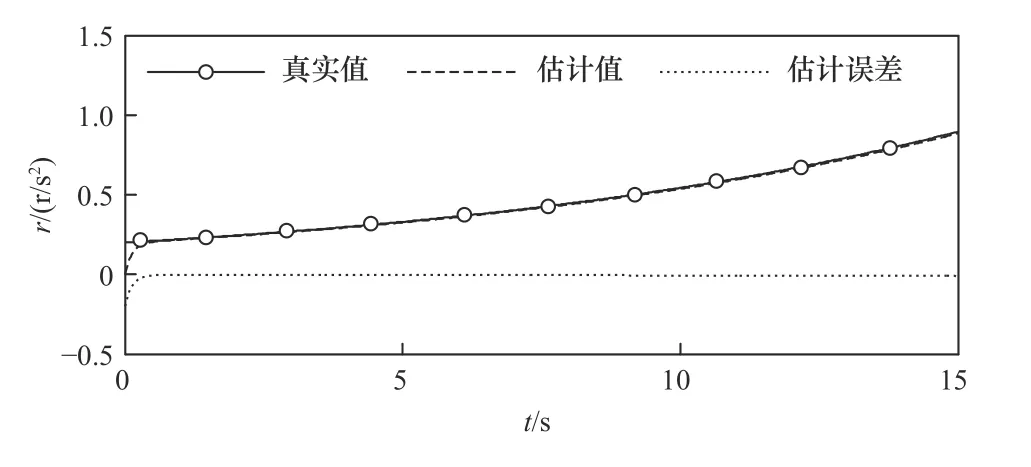
图7 复合干扰估计结果

4 测试平台及实验结果

为了验证设计的控制策略对永磁同步电机的实际控制精度，搭建了测试平台，测试平台主要由1.2 kW永磁同步电机（型号：110SYM04030）、转速测量仪（DYN-200）、电机驱动器（型号：SD200）、控制器（干扰信号和电流-脉冲隔离转换器）、动力电源（220 V/50 Hz）和可调负载等组成。测试系统原理图如图8所示。

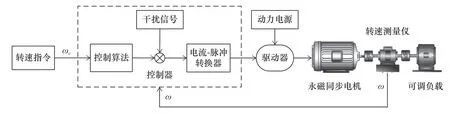
图8 测试系统原理图

控制器中可载入不同的控制算法，转速指令通过控制算法处理后输出控制电流，干扰信号是在控制器中模拟出的系统复合干扰信号，控制电流和干扰信号叠加后，经电流-脉冲隔离转换器输出脉冲信号，驱动器接收不同频率的脉冲信号来控制永磁同步电机运转，永磁同步电机和可调负载之间安装了转速测量仪，转速测量仪可实时测量电机的转速，并反馈给控制器，从而形成控制闭环。由于模拟出的复合干扰信号会影响到永磁同步电机的转速，测试实验中，通过测量不同控制方法下永磁同步电机的跟踪精度来验证控制效果。测试平台如图9所示。

图9 测试平台

实验中，通过主机向控制器发送命令，设定10个不同转速的指令信号，转速范围在100～1 200 r/min，模拟干扰信号电流为0.02sintA，并分别采用文献[17]和本文方法对永磁同步的转速进行控制，同时通过转速测量仪测量出实际的转速数据，得到的结果及误差数据如表3所示。

从表3的实验结果可看出：在文献[17]滑模控制方法的作用下，电机的实际最大转速误差为4.7 r/min，控制精度不高；而在本文控制方法的作用下，电机的实际最大转速误差仅为0.3 r/min，控制精度较高，二者对比突出了本文提出方法对永磁同步电机具有更优的实际控制效果。

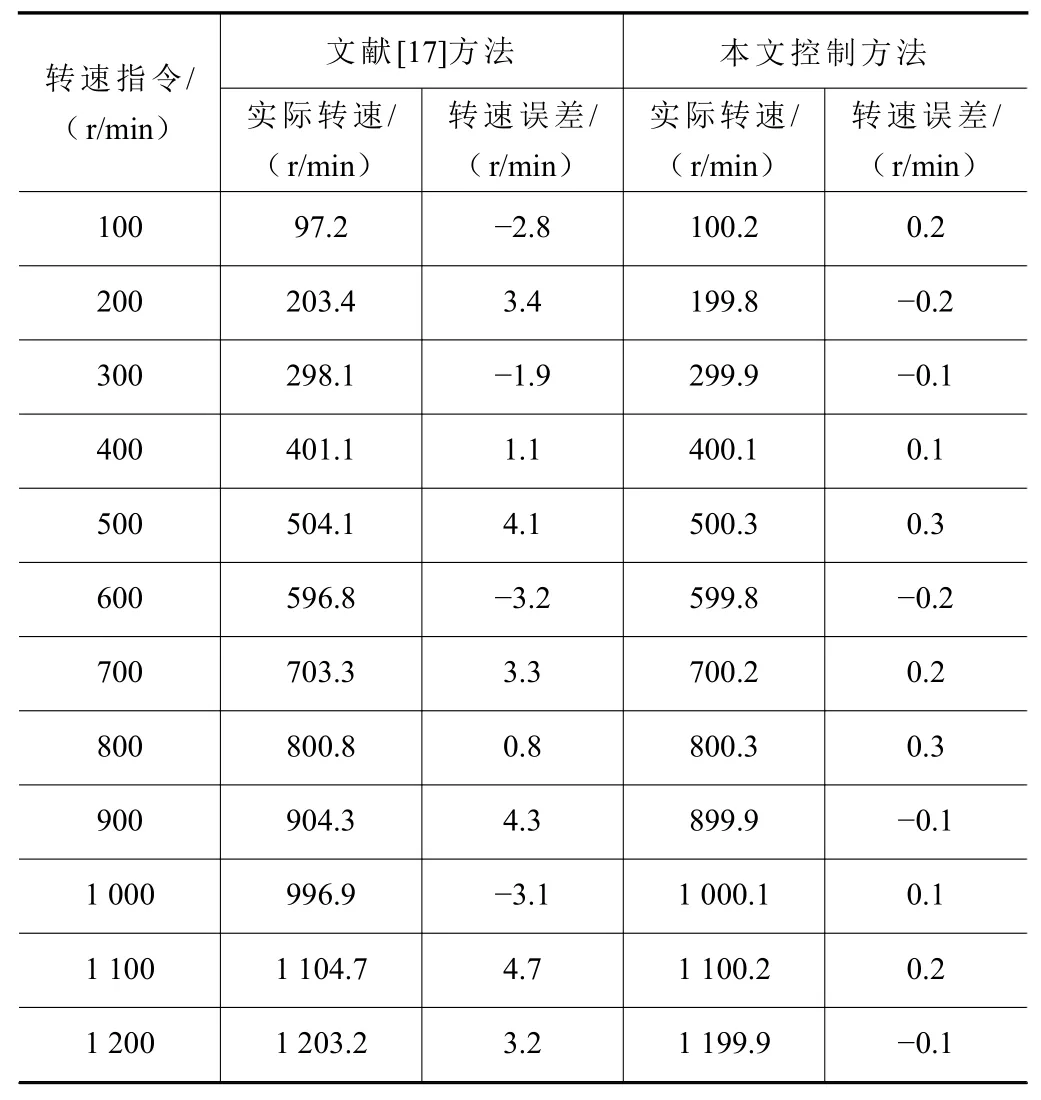
表3 实验结果

5 结语

针对数控机床永磁同步电机中的负载转矩扰动、电路和磁路扰动等因素影响，采用扩展滑模观测器设计了鲁棒控制方法。仿真结果表明：设计的鲁棒控制方法能够包容复合干扰的影响，确保永磁同步电机在0.4 s内稳定、准确跟踪指令信号，最大转速误差和转动加速度误差分别为0.1 r/s和0.05 r/s2；同时，设计的扩展滑模观测器可在0.4 s内准确估计出转速和转动加速度，最大估计误差分别仅为0.08 r/s和0.04 r/s2，也能够准确估计出复合干扰，估计误差也仅为0.03 r/s2。在测试实验中，提出方法对电机转速的最大跟踪误差仅为0.3 r/min，与其他方法相比表现出了更快的响应速度和更高的控制精度，具有更优的鲁棒性、快速性和准确性，实现了数控机床永磁同步电机的高精度转速控制。