基于最优环流的MMC直流侧功率稳定控制策略研究

石超，夏向阳，贺烨丹，邓文华，王灿，刘远，黄智，赵欣然

(1. 长沙理工大学电气与信息工程学院，湖南长沙，410114；2. 湖南长高高压开关集团股份公司，湖南长沙，410219)

2001年，MARQUART提出了模块化多电平换流器(modular multilevel converter，MMC)，这种新型多电平结构具有扩展性好、开关频率低、波形质量好等优点，在柔性直流输电领域潜力巨大[1-3]，而如何保证柔性直流输电系统正常运行和交流侧故障时直流侧功率的稳定传输是系统运行的关键。系统正常运行时，三相之间桥臂环流的2倍频分量相互抵消，不对直流侧功率产生影响。当交流侧网压不平衡时，环流中会出现2倍频零序分量，导致直流侧出现较大的2 倍频电流、电压波动等问题，引起直流侧功率发生振荡，经过直流传输线路传播到其他换流站，影响其他换流站的正常运行[4-8]。现有文献在网压不平衡条件下的控制策略主要包括以下2个方面。

1)外部控制以消除负序电流、有功功率、无功功率波动等为目标，内环则在桥臂环流中加入零序补偿环节，以此抑制直流侧功率发生振荡[9-14]。文献[9]提出了一种电网电压不平衡时的无差拍直接功率控制策略，省略了复杂的外环电流参考值计算环节。文献[10-11]针对外环3个控制目标控制精度和系统适应性问题等，对比例积分控制策略进行了改进。文献[12]分别以消除负序电流和有功功率波动为控制目标设计了双矢量电流控制策略，但该研究只是针对单个控制目标，但没有考虑变换器的内部动态特性，直流侧仍存在电压波动。文献[13]基于自适应锁相环，加入了功率补偿，可以实现抑制交流电流失衡、瞬时功率波动以及稳定系统直流电压、电流的多目标控制。文献[14]提出了一种电网电压不对称时精确环流抑制方法，通过补偿臂零序环流分量产生的零序电压来消除环流中零序分量，但没有给出控制策略所需的环流精确参考值。

2)从能量的角度出发，通过控制功率流向和控制桥臂电流同时实现对交流侧电流和环流、直流母线电流进行控制[15-17]。文献[15]认为通过控制桥臂电流可同时实现交流侧电流控制和环流抑制，且不需要考虑交流侧的瞬时功率波动。文献[16]通过调节直流分量在三相桥臂之间的分布来实现交流侧三相电流的平衡，并加入零序电流抑制器来抑制直流侧电压的波动，但其控制策略复杂，其中，电容电压平衡控制只适合子模块数量较少且使用载波调制的场合。文献[17]通过调节桥臂电流各分量来调节功率的流动，同时实现交流侧电流和MMC内部能量的协同控制，但直流侧功率仍然会存在振荡。文献[18]则提出了一种带有前馈补偿的交流电流、桥臂环流和直流电流的解耦控制策略及子模块电容电压和直流电压的平衡控制策略，能够有效抑制交流侧的功率震荡传播到直流侧，但该策略所需的控制器数量众多，且未考虑交流侧不同控制目标情况下的适用情况。

在电网电压不平衡时的交流侧外部3个控制目标中，对有功功率进行补偿，直流侧的电压能够保持稳定[9]，而即使实现了抑制负序电流和抑制无功功率2倍频波动这2个控制目标[19]，系统内部依然存在零序环流，直流侧功率仍然存在振荡。为此，本文在不改变网压不平衡时交流侧控制目标的前提下，从桥臂环流角度提出一种基于最优环流的MMC直流侧功率稳定控制策略，该策略无需零序补偿和交流侧功率补偿环节，利用MMC自身的能量缓冲能力，使得MMC在交流、直流系统间起“防火墙”的作用，避免了由交流电网不对称引起的功率振荡传播到直流系统的问题，并通过仿真验证所提策略的有效性。

1 MMC 能量缓冲机理及其数学模型

1.1 能量缓冲机理

MMC 单相平均值模型等效电路如图1 所示[20-21]。图1中，直流侧和交流侧的每一相都可以用1 个受控电压源和等效阻抗串联来表示，Ctot为单相桥臂等效电容，为j相上下桥臂电容电压的平均值，Pac为交流侧有功功率，Pdc为直流侧有功功率。

当交流侧网压不平衡时，交流侧会产生有功功率振荡，并且传播到直流侧中，根据能量守恒定律，要使直流侧功率无振荡，则桥臂电容可以在其裕度范围内充当防火墙的作用，吸收交流侧产生的任何类型的功率振荡。

1.2 拓扑结构与数学模型

三相MMC 由3 个相单元组成，其单相拓扑结构如图2 所示。图2 中：每个相单元由上下2 个桥臂(下标p 表示上桥臂，n 表示下桥臂)组成，每个桥臂由桥臂电感L0、桥臂损耗等效电阻R0和N个子模块(submodules,SM)串联组成；upj和unj分别为换流器上、下桥臂投入运行子模块电容电压之和；ipj和inj分别为换流器上、下桥臂电流；uvj和ivj分别为交流侧各相电压和电流；Lac为交流侧等效电感；uj为交流侧出口处电压；j为a，b 和c；udc为直流侧电压。

根据MMC的电路结构和基尔霍夫定律，得到MMC基本单元的时域数学模型为

上、下桥臂电流可以表示为

式中：icirj为j相桥臂环流。定义上下桥臂的差模电压为udiffj，上下桥臂的共模电压为ucomj。

由于桥臂电感储能较少，上、下桥臂中的能量Wpj和Wnj可近似用桥臂中所有子模块电容中储存的能量来表示：

式中：upji和unji分别为j相上、下桥臂第i个子模块的电容电压；uapj和uapj分别为j相上、下桥臂的平均电容电压。

对式(4)求差、求和得到上下桥臂瞬时功率之和和之差

2 最优环流参考值分析计算

2.1 拉格朗日乘数法的基本思想

在求解数学最优问题中，拉格朗日乘数法是一种寻找变量受1个或多个条件所限制的多元函数极值的方法。以二元函数z=f(x,y)和约束条件φ(x,y)为例，为了确定函数z=f(x,y)在约束条件下的极值点，首先需要先建立拉格朗日函数如下所示：

式中：x和y为任意变量；λ为拉格朗日参数。

对x，y和λ分别求一阶偏导，分别令其偏导数为0，从而解出相应的x，y和λ，再根据jianlde 方程组，便可解出满足约束条件的极值点(x,y)。

根据拉格朗日乘数法的定义可知，约束条件φ(x,y)= 0 是保持不变的，并且与常量x和y的取值无关。而在电力系统中，电压、电流都是由瞬时变化的周期量的叠加，因此，要满足约束条件的定义，只能取这些周期变化量的平均值。

本文根据系统运行的前提(即维持MMC 中电容电压稳定)，考虑到环流中各分量与桥臂能量的耦合关系，建立1 个周期内平均能量的硬性约束条件。

2.2 最优环流参考值计算

环流的存在会引起桥臂电流产生畸变，并增大其峰值和有效值，从而导致桥臂损耗增加，因此，需要降低环流icirj波动。本文用min表示最小，例如min →Δicirj就表示为环流的瞬时波动量Δicirj最小。当采用定直流电压控制时，直流母线电压udc基本不变。因此，可以在不改变函数目的的前提下重新表示为min →Δudcicirj。

由于存在瞬时目标函数和含瞬时周期量平均值的约束条件，并且变量为一阶，因而无法求解。为了避免这种情况，将其转化为所求变量平方的平均值，将瞬时目标函数转换为平均目标函数，又不丢失“瞬时”信息，建立如下目标函数：

式中：t0为初始时间；T为1个基波周期。

根据1.2节的分析，结合式(6)和式(7)，忽略环流压降ucirj，得到如下约束条件：

结合式(9)～(13)，根据拉格朗日乘数法的相关要求，建立如下拉格朗日函数：

为了得到环流的瞬时值，省略积分部分，对式(16)进行化简得

式(20)中右边第1 项为直流分量，用于调节各相上、下桥臂能量之和的平均值；第2项为基频分量，用于调节上桥臂和下桥臂之间的平均能量差。

在交流侧故障下，环流中不仅有正负序分量，而且有零序分量，三相环流之和并不为常量，因而，直流侧功率仍然存在振荡。

为了防止由MMC交流侧故障引起的功率振荡传播到直流侧，需要整合三相环流之间的关系，为此，引入1个新的边界条件：

将式(25)代入式(24)解得

再将求得的λ代入式(24)得到新的环流参考值：

即

3 整体控制策略

本文主要考虑在不同外环控制目标下，经过分析所得到的最优环流参考值能否有效抑制直流侧的功率振荡。整体的控制策略主要分为外环控制和环流控制2部分，其中，外环控制目标的选取已经有大量研究，因此，本文直接给出交流侧电流参考值。环流控制的目的是有效跟踪推导的环流参考值。

3.1 外环控制目标

根据电网电压不平衡情况下的影响，可将外环控制目标分为3 类：1)控制交流侧三相电流平衡；2)控制无功功率无脉动；3)控制有功功率无脉动。

在不加功率补偿以及零序抑制环节的情况下，在控制目标1和2的条件下，直流侧功率仍然存在振荡，而对于控制目标3，若加入功率补偿，则能够维持直流侧电压稳定。因此，本文主要针对控制目标1和目标2验证所提策略的有效性。

当电网电压不平衡时，由于变压器为Y/△接线，不存在零序分量，因此，交流侧的输出电压和输出电流可以分解为

式中：和分别为网侧交流侧输出电压的正、负序分量的幅值；和分别为交流侧电流的正、负序分量幅值；θ+和θ-分别为正、负序电压的初相角；φ+和φ-分别为正、负序电流分量的初相角；γ为相位差。

在dq坐标系下MMC 交流侧的瞬时复功率可以表示为[9]：

式中：θ1为d轴与两相静止坐标系下α轴之间的夹角；Ps0和Qs0分别为交流侧有功、无功中的直流分量幅值；Ps2sin和Ps2cos分别为有功2 倍正弦、余弦分量幅值，Qs2sin和Qs2cos分别为无功功率中2 倍频正弦、余弦分量的幅值。

用矩阵形式可以表示为

3.1.1 控制目标1：交流侧三相电流平衡

假设交流侧中的电流负序分量得到有效抑制，根据式(32)，可得到交流侧电流在d轴坐标系下的参考值和q轴坐标系下的参考值为

3.1.2 控制目标2：无功功率无脉动

抑制无功功率无脉动，即Qs2cos和Qs2sin均为0，则可以解得此时交流侧正负序电流在dq坐标系下的参考值为：

其中：

3.2 环流控制

由于上节推导的环流参考值中包含直流分量和交流分量，而PI 控制无法对交流信号进行无静差跟踪，为了有效跟踪环流参考值，在PI 控制的基础上加入谐振控制，构成PI-R 控制器，为了增加系统的稳定性，采用准PI-R 控制器[22]，其传递函数为

式中：Kp为比例系数；KI为积分系数；KR为谐振系数；ω0为谐振频率；ωc为截止频率。

得到总体的控制策略如图3 所示。图3 中，“ref”表示参考值，如ujref表示交流侧出口处电压uj的参考值。

4 仿真验证

4.1 仿真模型及参数

利用MATLAB/simulink 软件搭建37 电平MMC-HVDC 仿真模型，模型的相关参数如表1 所示，故障点和简化模型如图4所示。

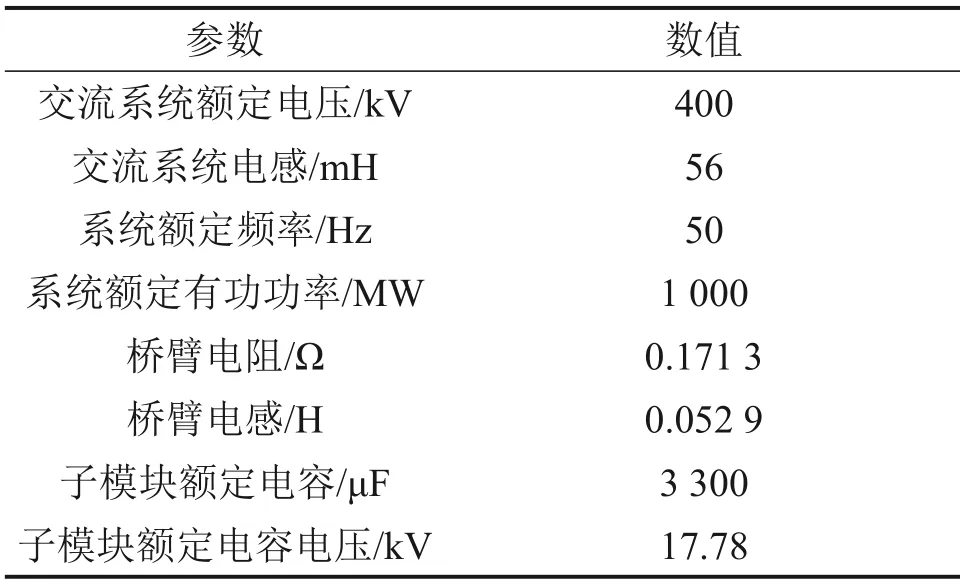
表1 仿真平台主要参数Table 1 Parameters of simulation platform system

4.2 仿真结果

为了验证所提控制策略的有效性，在MMC交流侧网压不平衡条件下，对交流侧外部选用不同的控制目标进行仿真验证，并与采用直接环流抑制策略(CCSC)时直流侧功率的振荡情况进行对比。

系统一开始处于稳定运行状态，在1.4 s 时电网A 相电压标幺值下降50%，故障持续0.2 s，阀侧电压如图5所示。

4.2.1 控制目标1：抑制负序电流

抑制负序电流的仿真结果如图6所示。在电网电压不平衡区间段(1.4～1.6 s)，阀侧三相电流依然能够保持对称(见图6(a))。图6(b)和图6(c)中负序分量得到了有效抑制，但负序电压的存在使得交流侧有功、无功功率出现了2倍频脉动。环流控制策略能有效跟踪环流参考值，环流中的2倍频分量也得到有效抑制，如图6(d)所示，但还存在一些低次谐波分量(图6(e)和图6(f)中)，三相桥臂能量并不相等，需要对交流侧功率进行补偿。由于MMC自身具有能量缓冲能力，直流侧功率能够维持稳定传输。

4.2.2 控制目标2：抑制无功功率波动

当外环采用抑制无功功率为目标时，仿真结果如图7所示。图7(a)中，由于负序电流没有得到抑制，阀侧的三相电流依然不对称，无功功率能够保持恒定，有功功率依然存在波动(如图7(c)和图7(b)所示)。环流能够有效跟踪参考值，二次谐波分量得到了有效抑制，但还存在着一些低次谐波分量。不同的外环控制目标对能量波动的影响不同，采用控制目标2时，桥臂中总的能量波动更大，需要对交流侧的功率振荡进行补偿。由于能量的缓冲作用，直流侧功率仍然能够稳定传输。

为了验证本文所提出的最优环流的优越性，将其与交流侧故障时采用传统的环流抑制策略(CCSC)进行对比，仿真结果如图8 所示。交流侧在0.2 s时发生不平衡故障，故障持续时间为0.4 s，发现当采用CCSC时，直流侧功率振荡明显，而本文推导的最优环流则能够有效抑制直流侧功率的振荡。

5 结论

1)直接在abc坐标系下得到的最优环流参考值简化了正负序分解以及dq变换的过程，能够有效降低环流的波动，且不需要加入零序补偿环节。

2)本文所提出的最优环流充分利用了MMC自身的能量缓冲能力，使MMC在直流侧和交流侧之间充当了防火墙的作用，在不同工况和不同类型的外环控制目标下，都可以及时对交流侧功率的振荡进行能量补偿和调节，有效确保了直流侧功率的稳定传输。

3)在MMC实际运行过程中，不一定要求三相桥臂能量完全相同，但子模块电容电压波动的裕度是有限的，因此，下一步将对交流侧故障时MMC自身最大缓冲能力的范围进行研究，并通过实验进行验证。