双伪逆权值确定的极限学习机算法及其在乳腺肿瘤诊断中的应用

龙求青，廖柏林，印煜民，代建华

(1. 吉首大学信息科学与工程学院，湖南吉首，416000；2. 湖南师范大学信息科学与工程学院，湖南长沙，410081)

极限学习机(extreme learning machine,ELM)算法作为单隐含层前馈神经网络(single hidden layer feed forward neural network, SLFNs)中一种全新的学习算法，凭借其训练速度快、泛化性能优[1]等特点，吸引了该领域大批学者的关注与研究。与传统的神经网络算法(如误差反向传播算法[2-3]等)不同，该算法的核心思想为：网络的输入权值和隐含层偏置随机产生，且其数值在训练过程中保持不变，其输出权值则是通过将平方损失函数最小化，再求解伪逆运算得到最小范数最小二乘解[4]。整个训练过程不需迭代，仅需设定隐含层的神经元个数和激活函数。目前，ELM在疾病(如乳腺癌等)诊断[5]、交通标志识别[6]、智能决策[7]等方面获得了广泛应用。

然而，ELM 算法的输入权值、隐含层偏置和隐含层神经元数的不确定性会对其预测性能和算法的稳定性产生较大的影响[8-9]。张文博等[10]指出，当完全随机选择输入权值与隐含层偏置等参数时，ELM 的性能并不总是最优的，同时，这也是导致ELM 算法隐含层神经元数冗余的重要原因[11]。对此，学者们提出使用群智能优化[12-14]、剪枝法[15-16]和自适应[17-18]等算法对ELM 算法进行优化，以提高其整体性能。在实际应用中，虽然这些算法确实能够优化隐含层神经元数，但又引入了大量的超参数，并且这些参数通常需要进行反复迭代寻优才能得到，增加了算法的计算复杂度，导致其难以应对实时性要求高的现实问题。为此，本文作者提出双伪逆权值确定的极限学习机(double pseudo-inverse weight determination ELM, DPELM)算法，即首先采用伪逆法来确定ELM的输入权值，随后再次使用伪逆法确定输出权值。最后，采用本文提出的DPELM对乳腺肿瘤进行快速分类，以验证该算法的分类识别准确率。

1 改进的极限学习机算法

1.1 极限学习机算法

设有N个任意不同的样本集(xi,yi)，其中，xi=(xi1,xi2,…,xin)T∈Rn，为输入向量(样本的特征)；yi=(yi1,yi2, …,yim)T∈Rm，为对应的样本标签向量。在输入神经元个数为n、隐含层神经元个数为L和输出神经元个数为m且激活函数为f(·)的ELM网络中，ELM的运算模型可以表示为如下形式：

式中：i=1，2，…，N；wj=(wj1,wj2,…,wjn)，为隐含层第j个神经元与输入层神经元的权值向量；bj为第j个隐含层神经元的偏置；βj=(βj1,βj2,…,βjm)，为隐含层第j个神经元与输出层神经元的权值向量；yi为对应于样本xi的期望输出向量。式(1)可以进一步简化整合为如下矩阵表达式：

式中：Y=[y1,y2,…,yN]T，为训练样本期望输出矩阵；β为输出权值矩阵。

在ELM 中，H被称为随机特征映射矩阵[19]。当隐含层神经元参数(wi,bi)随机生成并给出训练样本之后，矩阵H即为已知，且在整个训练过程中其值都不会改变。此时，式(2)就转化为求解其最小二乘解=H+Y，其中，H+为隐含层输出矩阵H的伪逆。

1.2 改进的极限学习机

双伪逆权值确定的ELM 也由输入层、隐含层和输出层构成。式(1)还可以写为如下矩阵表达式：

式中：Y=[y1,y2,…,yN]T∈RN×m；X=[x1,x2,…,xN]T∈RN×n；B= [b1,b2,…,bL]T∈RL×1，为偏置矩阵；W为输入权值矩阵，

随着人类的生存与发展，水污染逐渐成为威胁人们健康的重要因素之一，泌尿系结石是水污染造成的较为常见疾病之一。由于年龄、性别、职业、饮食结构、水分摄入量、气候、遗传等因素的不同，我国1980年和2003年做过两次的调查，泌尿系结石的发病情况大约是黄河以北为10%，长江以南为25%，其中男性患有泌尿系结石的比例明显高于女性[5]。泌尿系结石是尿中形成的结石晶体呈超饱和状态，是形成结石的主要原因。结石通常可出现在膀胱、输尿管等部位，临床表现为一侧腰部的剧烈疼痛，有腹胀、恶心、呕吐、程度不同的血尿、排尿困难和排尿疼痛等症状，对患者的生活造成严重影响。根据结石的位置选择适当的方法，能有效治愈泌尿系结石。

定理1：假设激活函数f(·)为严格单调函数，输出权值β和偏置矩阵B分别选自区间[a1，a2]和[a3，a4]，则最优的输入权值矩阵W=(f-1(β+Y)+B)X+，其中f-1(·)表示f(·)唯一的反函数。

证明：将式(3)两边同时乘以β+，得到

求解式(4)的反函数， 得到f-1(β+Y)=WX-B，即

将式(5)两边同时乘以X+，得到WXX+=(f-1(β+Y)+B)X+， 即W=(f-1(β+Y)+B)X+。证明完毕。

在得到最优的W之后，再次使用伪逆法确定最优的输出权值。可以通过下式求得：(f(WX-B))+。至此，输入和输出权值均为使用解析式计算而求得的最优值。

1.3 双伪逆权值确定的ELM算法训练过程

双伪逆权值确定极限学习机的具体算法训练过程如下：

1)在某一特定的区间内对输出权值矩阵β和隐含层神经元偏置矩阵B进行随机初始化；

2)在训练样本确定的情况下，根据公式W=(f-1(β+Y)+B)X+，计算出最优输入权值W矩阵；

4)将最优输入权值矩阵W、最优输出权值矩阵以及偏置矩阵B用于测试集测试。

2 双伪逆权值确定的极限学习机算法的性能评估

从UCI数据库中随机选择6个数据集，对改进后的极限学习机算法进行分类性能评估。

2.1 实验描述

为验证改进后算法的性能，本文通过Matlab平台，从算法的预测精度、算法所需的隐含层神经元个数以及算法输出结果的稳定性3个方面对原始ELM 和本文算法进行比较。为证实算法的普遍适用性，本实验从UCI 数据库中选取6 个数据集(包含3 个二分类数据集和3 个多分类数据集)作为实验数据集。各数据集的描述如表1所示。

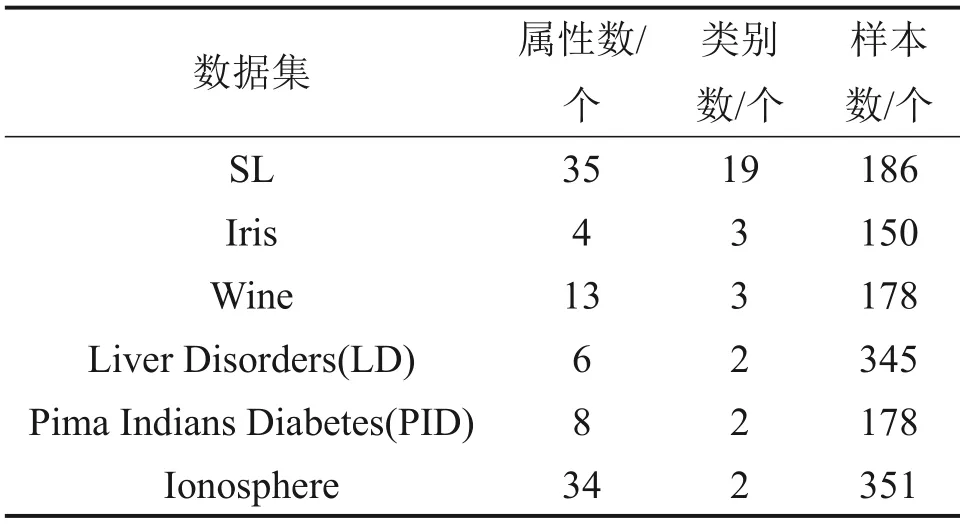
表1 实验数据描述Table 1 Description of experimental data

2.2 实验结果及分析

通过实验比较传统ELM 和本文算法中隐含层神经元个数对模型预测性能的影响。首先，随机选取各数据集中70%的数据为训练样本，30%的数据为测试样本，训练和测试样本划分好后固定不变，采用生长法确定隐含层神经元个数，即每次增加1个神经元观察准确率的变化，当准确率不变或变化值小于所设定的阈值时，确定其为相应算法最好的网络结构。然后，在各算法最优的网络结构下运行ELM 算法和本文算法各100 次，计算其测试集的平均分类准确率。本实验选择tan函数作为激活函数，其反函数为arctan函数。不同算法分类准确率及隐含层神经元个数对比及其达到最高分类准确率时所需的隐含层神经元个数对比如表2所示。

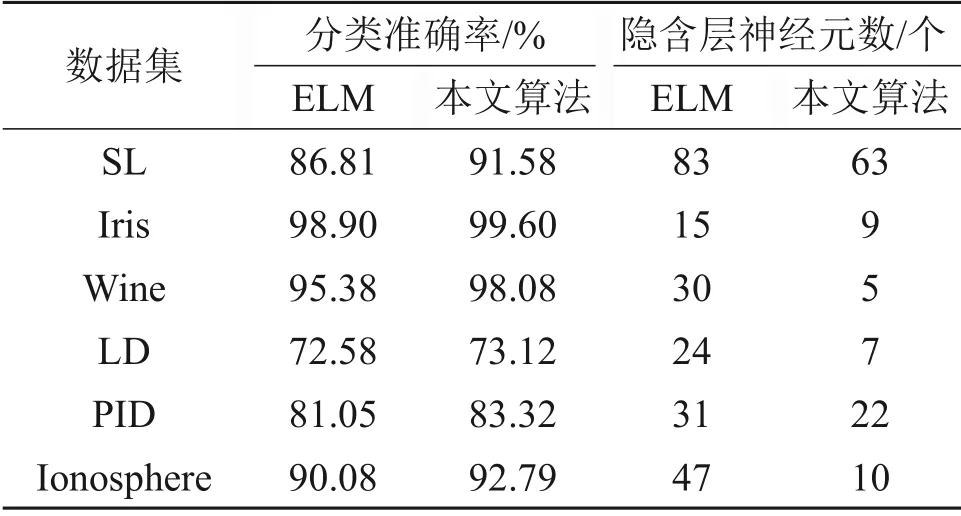
表2 不同算法分类准确率及隐含层神经元个数对比Table 2 Comparisons of classification accuracy and number of hidden layer neurons of different algorithms

由表2可以看出，无论是在二分类数据集还是在多分类数据集中，本文所提算法的分类性能均比传统的极限学习机算法分类性能有所提升。本文所提算法达到最高分类准确率时所需要的隐含层神经元个数更少，网络结构更为简单，由此可见本文采用的通过解析式确定输入权值方式所得结果要优于随机确定输入权值方式所得结果。同时，为进一步分析算法参数对分类性能和算法稳定性的影响，本文在二分类问题和多分类问题中各选取1个数据集，对其算法性能进行比较。

选取多分类的SL 数据集和二分类的LD 数据集，其训练集与测试集依然按照7:3 的比例划分，样本划分好后固定不变。设定隐含层神经元数从1递增至100 个，每增加1 个神经元都执行100 次ELM 算法和本文算法，观察实验结果的均值、方差、极差的变化趋势，结果分别如图1 和图2 所示。图1和图2中，黑色五角形所示位置为各算法取得最高分类准确率的位置。

从图1(a)和图2(a)可以看出，随着隐含层神经元个数不断增加，传统ELM 和本文算法的预测准确率均先迅速上升，而后趋于平缓或下降。根据实验结果及文献[20]中的定理，可知本文算法和传统的极限学习机算法有同样的特性，即随着隐含层神经元个数增加，算法的拟合性能越来越好，但当拟合性能达到某个极值点后，继续增加隐含层神经元个数，则会出现训练样本过拟合的现象，而测试样本的分类准确率增速缓慢甚至开始下降。由图1和图2还可以看出，无论是在多分类的SL数据集还是在二分类的LD数据集中，随着隐含层神经元数的增加，本文所提算法的分类平均准确率的上升速率均比传统的极限学习机算法的快，且所需要的隐含层神经元个数均要比传统的极限学习机算法的少。从方差和极差结果可以看出，本文所提算法在SL 和LD 数据集中的方差和极差均要比传统的极限学习机算法的小，说明本文算法的稳定性优于传统极限学习机算法的稳定性。

3 双伪逆权值确定的极限学习机算法在乳腺肿瘤诊断中的应用

为了进一步验证双伪逆权值确定极限学习机算法的准确性，本文将其应用于乳腺肿瘤诊断的分类识别；采用多种不同的算法对同样的乳腺肿瘤训练集、测试集分别进行学习和识别，并与本文方法的性能进行对比。

3.1 实验环境

实验用计算机CPU 型号为Intel i5-4200U(1.6 GHz)，内存为4 GB，操作系统为Windows 7，实验软件为Matlab2012(b)。

3.2 实验数据

本实验数据来自美国威斯康星大学医学院所发布的公开数据集(Wisconsin Breast Cancer Database)，包含有569个乳腺肿瘤病例，其中良性357 例，恶性212 例。本文随机选取450 组肿瘤数据(良性病例数为282，恶性病例数为168)作为训练集，剩余的119 组肿瘤数据(良性病例数为75，恶性病例数为44)为测试集。每例样本由从乳腺肿瘤样本数据中提取的10 个特征值的均值、标准差和最大值共30个数据组成。

3.3 实验结果与分析

选取各算法的良性肿瘤平均确诊率(简称良性确诊率)、恶性肿瘤平均确诊率(简称恶性确诊率)以及平均诊断准确率这3个性能指标进行比较。为了增加比较的可靠性，对本文算法、改进鱼群算法优化的ELM、人工鱼群优化的极限学习机算法(AFSA-ELM)、ELM、学习向量量化算法(LVQ)和误差反向传播算法(BP)等[21]分别进行20 次独立实验，取其良性确诊率、恶性确诊率、平均准确率、假阴性率的平均值进行比较，其中改进鱼群算法优化的ELM，AFSA-ELM，ELM，LVQ和BP等算法的实验结果来自文献[21]，比较结果如表3所示。

<1)，且各件产品是否为不合格品相互独立．

由表3可见，本文所提算法的良性确诊率、恶性确诊率、平均准确率均比其他算法的高，而假阴性率比其余算法的要低，说明本文所提算法可以快速准确地识别恶性肿瘤，降低了由于误诊而导致的延误治疗、影响治疗效果的风险。

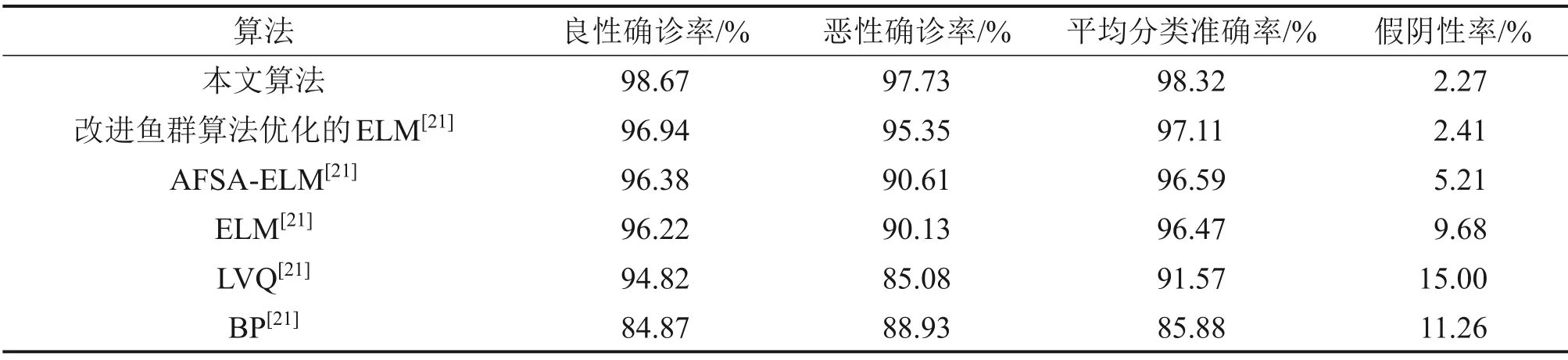
表3 多个算法的性能对比Table 3 Performance comparison of multiple algorithms

4 结论

1)在6个随机选取的UCI数据集中，本文所提出的基于双伪逆权值确定的极限学习机(DPELM)算法分类性能较传统的极限学习机(ELM)算法分类性能都有不同程度提升，其中，SL 数据集的分类准确率提升幅度最大，为4.77%；LD 数据集的分类准确率提升幅度最小，仅提升了0.54%。

2)改进后算法达到最佳分类准确率时，所需隐含层神经元个数比传统ELM 算法的更少，网络结构更简单。

3)改进后算法在SL 数据集和LD 数据集测试实验中的方差和极差更小，说明算法的稳定性更优。同时，其在乳腺肿瘤分类识别实验中，诊断性能较改进鱼群算法优化的ELM，AFSA-ELM，ELM，LVQ 和BP 等方法的诊断性能均有所提升，表明本文所提算法在乳腺肿瘤辅助诊断中具有分类准确率高、假阴性率低的优点，本文方法用于乳腺肿瘤辅助诊断是可行的。