表面共振圆环结构对Si纳米线热传导的调控

孙 博， 熊世云， 张定波， 曹增强， 陈元正， 王 辉， 王红艳， 倪宇翔

(1. 西南交通大学 物理科学与技术学院， 成都 611700；2. 苏州大学 功能纳米与软物质实验室， 苏州纳米科技协同创新中心， 苏州 215123)

1 引 言

热电材料是一种利用材料内部载流子运动实现热能和电能相互转化的功能性材料，高效热电材料在清洁能源开发、废热回收再利用等领域有着广泛的应用[1]. 热电材料的效率正比于塞贝克系数的平方和电导率，反比于热导率. 因此，如何有效地抑制声子输运来降低材料的热导率成为了热电领域亟待解决的难题. 当材料尺寸进入微纳尺度，由于尺寸效应的影响[2, 3]，其性质会受到极大的改变[4-6]. 研究表明，当Si从块材料变为纳米线或纳米薄膜时，热导率会降低一个数量级[7, 8]. 对材料在微纳米尺度进行结构设计，以进一步阻碍声子的传输，将有利于其热电效率[9-16]的提升.

声子是晶格振动能量的量子化形式，它虽然是一种准粒子[16]，但也同时具备粒子性和波动性. 利用声子的粒子性，在材料中引入界面、缺陷、杂质等散射源可以增加声子的散射[12, 17-20]，从而降低热导率. 但在这些情况下同时也会增加电子的散射[21]而影响材料的电导率，这是不利于热电应用的. 从声子的波动性出发，利用声子共振效应来抑制声子的热输运可有效降低材料的晶格热导率[22]，同时，对电输运不会造成不利的影响，因而在近年来得到了广泛的研究. 通过在结构表面引入共振结构，处于共振频率下的声子将与该频率附近声学支的声子发生杂化，导致在声子色散关系中出现一系列的平带，显著降低声子的群速度，从而制约热传导. 例如，Xiong等人[23, 24]利用分子动力学模拟研究了硅基共振结构的热传导性质，结果表明，具有分支的Si纳米线可以在较宽的频率内产生声子共振效应，实现了超低热导结构设计. Honarvar等人[25]在Si纳米薄膜表面引入纳米柱，使热导率降低130倍. Zhang等人[26]提出一种新型的表面螺纹共振结构，相较于传统共振结构，进一步降低了硅纳米线的热导率. Feng等人[27]在硅基中嵌入Ge纳米粒子，实现了多模态声子共振，有效抑制了低频下声子的传输. 最新研究表明，声子共振除了降低声子群速度外，还能大幅减小低频声子的弛豫时间[23]，从而实现对低频声子输运的调控.

目前，对声子共振结构的高度和宽度变化对于基底材料热传导性质的影响还没有系统的研究. 如何通过改变共振结构的尺寸来调控晶格热导率？共振结构的高度和宽度是否存在一个最优值，来最大程度地发挥声子共振效应？本文拟通过分子动力学方法[28, 29]，探索Si纳米线表面共振圆环的高度和宽度对主干纳米线热导率和共振效应的影响，并揭示其背后的物理机制，以回答上述问题.

2 结构模型与计算方法

图1是用于分子动力学模拟的模型结构示意图. 沿着[1 0 0]晶向对硅进行切割，得到图1(a)所示的圆柱状纳米线，其表面具有圆环形状纳米分支，圆环与主干Si纳米线之间的界面上晶格完美匹配. 纳米线长度为2.72 nm，主干纳米线的半径为1.43 nm. 设置圆环的高度范围为0.5-3 nm，宽度范围为0.54-1.63 nm，以研究圆环尺寸对Si纳米线热输运性质的影响.

图1 共振圆环Si纳米线原子结构模型. 为了区分结构，用红色和黄色分别表示主干纳米线和共振圆环结构. (a)为正视图，(b)为截面图Fig. 1 (a) Model of the atomic structure of Si nanowires with the resonant annulus. In order to distinguish the different parts in the structure, the trunk nanowire and the resonant annulus structure are represented in red and yellow, respectively. (a) a positive view , (b) a cross-section

利用LAMMPS软件[30]进行平衡态分子动力学计算(EMD). 采用Stillinger-Weber(SW)作用势[31]来描述Si原子之间的相互作用，该势函数能准确模拟Si纳米线的热传导性质[32]. 模拟的时间步长设置为0.5 fs. 由于研究体系处于纳米尺度，为了减小尺寸效应带来的影响，模拟时采用周期性边界条件. 首先在NPT系综下弛豫400 ps，然后在NVT系综下继续弛豫400 ps，使系统的温度稳定在300 K左右，最后在NVE系综下模拟了500 ps，系统达到平衡. 基于格林-久保(Green-Kubo[33])公式计算纳米线的热导率：

(1)

式中，κz是沿纳米线轴线方向的热导率，kB是玻尔兹曼常数，V代表系统的体积，T是温度，t是关联时间，J是单位体积热流，“< >”表示统计平均，在分子动力学模拟中表示对时间原点的统计平均. 此外，为了减小模拟计算的误差，在系统弛豫后，我们对每个结构再进行20次独立的模拟，得到20个跑动热导率，然后再对这些数据进行平均，得到体系最终的热导率.

3 结果与分析

3.1 共振圆环高度、宽度对硅纳米线热导率的影响

采用EMD方法计算了不同共振圆环高度、宽度下Si纳米线的热导率，如图2所示. 从图2(a)可以看出，原始Si纳米线(圆环高度为0)的热导率为4.23 W/mK. 当我们在其表面加入高度为0.5 nm的圆环后，热导率降低了16.3%. 造成热导率明显下降的原因是共振圆环中产生了声子驻波，在相应的频率与主干纳米线中的声子发生了杂化，导致主干纳米线中的声子传输受到了阻碍. 随着圆环高度的增加，纳米线的热导率继续减小，并且其减小的趋势逐渐变缓. 当圆环的高度增加到2 nm以后，虽然热导率稍有降低，但其减幅很小. 研究的各模型中，减幅最大可达61.9 %. 热导率随圆环高度的增加而减小，是由于高度增加引起的共振圆环体积变大，因而能够提供更多的声子驻波参与杂化，从而增强共振效应并阻碍声子输运[25].

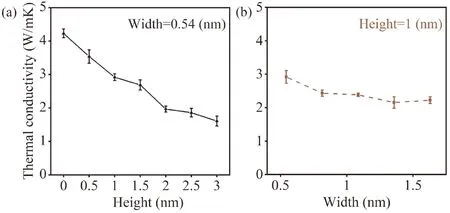
图2 不同圆环高度(a)、宽度(b)下的Si纳米线热导率Fig. 2 Thermal conductivity of Si NWs varying with the heights (a) and widths (b) of resonant annuluses.

接下来，我们研究共振圆环的宽度对纳米线热导率的影响. 将圆环高度固定为1 nm，在0.54-1.63 nm范围内调节圆环宽度，计算对应纳米线的热导率. 如图2(b)所示，随着圆环宽度的增加，纳米线热导率虽然有所减小，但是对比于热导率随圆环高度减小的趋势，其变化的幅度较小，所以影响纳米线热导率的主导因素是圆环的高度.

3.2 声子色散关系和声子群速度

为了进一步理解共振圆环引起的声子共振效应，我们利用晶格动力学计算了声子色散关系[32]:

D(k)ε=ω2ε

(2)

D(k)是质量归一化的动力学矩阵，可以由MD模拟中SW势函数的二阶导数得出，k为波矢，ε是原子振动向量，通过求解D(k)的特征值可以得到声子的频率ω，进一步可以得到ω-k的对应关系，即为所求的声子色散关系. 根据声子色散关系，可得到热传导方向上的声子群速度：

(3)

原始的圆柱形纳米线以及不同圆环高度、宽度下纳米线的声子色散关系分别如图3、图4所示，图5则显示了不同圆环高度下纳米线的声子群速度. 从图3可以看出，相比于原始的Si纳米线，共振圆环的引入将形成声子驻波，并在共振频率附近与主干纳米线中的声子发生耦合，使声子带出现展平现象，声学支的斜率明显降低，对应的声子群速度减小. 随着共振圆环高度不断增加，在整个布里渊区出现了一系列平坦的声子带. 圆环高度越大，提供的声子共振模式就越多. 相比于原始纳米线，具有共振圆环的Si纳米线的声子群速度也会有明显的降低，如图5所示. 当共振圆环高度增加到2 nm以后，声子群速度略有下降，但是下降幅度很小.

基于声子色散关系，统计了相应结构的最低共振频率，如图6所示. 随着共振圆环高度增加，由于局域共振作用，高频部分中大量光学模式出现了声子带展平效应，对声子色散曲线造成挤压，使得色散曲线整体向低频移动，最低共振频率不断降低. 共振圆环中产生的声子驻波波长的倒数正比于共振频率，在共振频率逐渐减小至不变的过程中，驻波波长逐渐增大. 当圆环高度增加到2 nm以后，驻波波长已基本不再变化，说明此时共振圆环中的声子与主干中的声子共振作用已达到最强，圆环中提供参与耦合的声子驻波已经达到饱和. 高度再增加，由于声子驻波波长的限制，共振作用不会再增大.

反观不同圆环宽度下纳米线的声子色散关系，则变化很小，如图4；并且纳米线的最低共振频率变化也很小，如图6(b). 可见圆环宽度变化对声子的传输影响较小.

图3 具有不同共振圆环高度的Si纳米线在0-3 THz内的声子色散关系.Fig.3 Phonon dispersion relations in the frequency range [0, 3] THz for pristine Si NW and Si NWs with different heights of resonant annuluses.

图4 具有不同共振圆环宽度的Si纳米线在0-2 THz内的声子色散关系.Fig. 4 Phonon dispersion relations in the frequency range [0, 2] THz for Si NWs with different width of resonant annuluses.

图5 具有不同共振圆环高度的Si纳米线的平均声子群速度.Fig.5 Averaged phonon group velocities of Si NWS with resonant annuluses of different heights.

3.3 不同声子模式贡献的归一化热导率分布

为了更加直观的理解共振圆环高度对Si纳米线共振效应的调控，我们计算了不同声子模式贡献的归一化热导率分布[34]：

(4)

式中，Ax为垂直于热传导方向上纳米线的厚度，Az为纳米线的长度，在我们的结构中，Ax=2.86 nm，Az=2.72 nm，k、vg、C、τ分别是波数、声子群速度[35，36]、比热容、声子散射时间. 结合声子色散关系进行着色，用颜色的暖度和冷度来表示不同模式下声子贡献的热导率大小：贡献越大，颜色越暖；贡献越小，颜色越冷. 图7显示了分解于色散关系上的热导率分布. 从图7(a)可以看出，低频模式(<3 THz)下，色散关系曲线颜色较暖，原始Si纳米线的热导率主要来自于低频声子的贡献. 引入共振圆环后，如图7(b)，声学支部分的LA、TA曲线颜色由暖色向冷色过渡，在相同波矢下(如k=0.3时)，声子模式在向低频移动的同时，其颜色也逐渐向冷色转变，光学模式中出现了少量的暖色模式，预示着共振效应使得声学支对热导率的贡献降低，从而导致光学支对热导率的相对贡献增大. 随着圆环高度增大，相同波矢下的声子模式进一步向低频移动，声学支颜色进一步向冷色变化，光学模式中的暖色也逐渐增多. 当高度达到2 nm以后，热导率分布基本不再改变，说明高度的影响作用已达到最大，这与我们计算得到的热导率数据相吻合. 声学模式下，Si晶体内原子作整体运动，这是物体热导率的主要来源. 声子共振效应增强使得声学支声子进一步被极化，导致纳米线热导率降低；光学模式下，原子作相对运动，对热导率贡献不大，这也是在共振圆环高度较大的模型中，尽管光学模式中暖色增加，硅纳米线热导率却依然降低的原因所在.

图6 共振圆环在不同高度(a)、宽度(b)下，从Si 纳米线声子色散关系中统计的最低共振频率Fig. 6 The lowest resonance frequencies of Si NWS withresonant annuluses of different heights (a) and widths (b), according to the phonon dispersion relations of Si NWS.

图7 各模型中不同声子模式贡献的归一化热导率分布.Fig.7 The distributions of normalized thermal conductivity contribution from different phonon modes in different models.

此外，在不同圆环高度下，我们统计了声学支声子对总热导率的贡献占比，如图8所示. 该图进一步证实声学支声子对总热导率贡献的降低，是共振环高度增加导致热导率下降的主要原因.

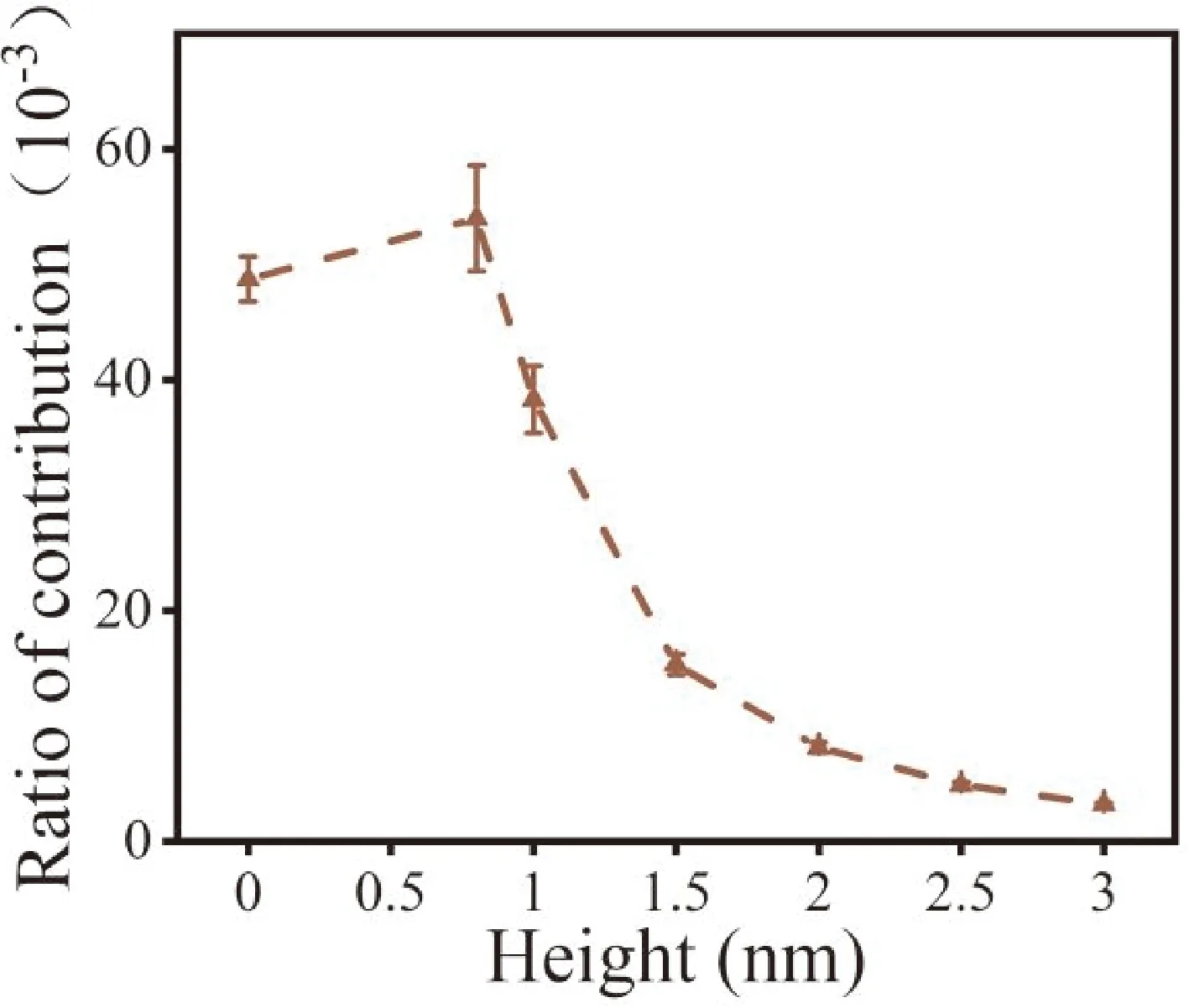
图8 不同圆环高度下声学支声子对总热导率的贡献占比.Fig.8 The ratios of total normalized thermal conductivity contribution of three acoustic branches in the whole at different annulus heights.

4 结 论

在本工作中，我们将表面圆环作为Si纳米线的声子共振结构，用于阻碍声子的传输. 通过平衡态分子动力学模拟研究了圆环尺寸对硅纳米线传热性质的影响. 研究发现，共振圆环可以产生声子驻波与主干Si纳米线中的声子发生共振效应，随着共振圆环高度的增加，纳米线热导率降低. 圆环高度增加到2 nm时，共振效应达到最大，之后继续增加圆环高度，纳米线热导率不再降低. 圆环的宽度对热导率的影响则并不明显. 声子色散关系、声子群速度以及不同声子模式对总热导率的贡献分布表明，共振圆环高度增加可以增大声子谐振器中产生声子驻波的最大波长，从而可以提供更多的声子参与杂化，增强声子共振效应，减小声学模式对热导率的贡献. 但是圆环高度的影响是有限的，当高度达到2 nm以后，声子共振效应会趋于饱和；改变圆环的宽度对声子传输能力的影响则不明显. 因此，通过调控共振支的高度来调节声子共振效应，是调控Si纳米线热传输的有效手段. 本文的研究结果对于高效热电材料的结构设计具有一定的参考价值.