铷原子低次谐波产生中的载波拉比振荡特征

李英娟， 管 仲， 景文泉， 魏 盼， 赵松峰

(西北师范大学 物理与电子工程学院, 兰州 730070)

1 引 言

激光与物质相互作用产生的高次谐波(HHG)有很好的应用前景，如获得从极紫外到软X射线波段的光源、合成超短阿秒脉冲等，高次谐波一直以来是强场物理领域的热点课题[1-3]. 对于平台区和截止位置附近的谐波，三步模型[4]成功地解释了谐波产生的过程. 因为低阶谐波的产生涉及束缚态-束缚态之间的相互作用，使得产生过程更加复杂，目前低阶谐波的产生机制还存在争议. 近几年，人们对原子分子的阈下谐波进行了大量研究, 包括谐波的产生机制和优化控制. 最近，利用碱金属原子研究共振波长驱动下的拉比振荡[5]及载波拉比振荡下的谐波引起了人们的关注.

电子在共振激光场驱动下，从基态到激发态再回到基态的过程叫做拉比振荡[6-12].一般来说，拉比振荡的周期和激光周期相差较大，但随着激光强度变大，当拉比振荡周期和激光脉冲周期可比拟时，则会出现载波拉比振荡. 我们用图1所示的布洛赫(Bloch)球直观地描述共振情况下的拉比振荡. Bloch矢量由u、v、w组成，其中，u为光极化的实部，v为光极化的虚部，w为两能级体系的反转粒子数. Bloch矢量在uv平面内绕w的振荡称为光极化，Bloch矢量在vw平面内运动决定了布居差的演化，当Bloch矢量转动到北极时，表明原子处于激发态，当Bloch矢量转动到南极时，则原子处于基态. 图 1(a)为脉冲面积为2π的脉冲驱动下， Bloch矢量沿着布洛赫球表面运动的示意图(此时，拉比振荡周期大于光学周期). 当Bloch矢量从南极螺旋上升到北极时，表明所有处于基态(价带)的电子从南极开始，沿着Bloch矢量螺旋上升至北极，即所有电子处于激发态(导带)，之后在激光作用下，再次返回南极，这一过程会对光极化实部u具有调制作用，所以导致光极化谱线中出现了两个峰. 图1(c)显示了脉冲面积为4π的脉冲驱动下的电子运动. 此时，拉比振荡周期等于光学周期.从图中可以看到，沿着Bloch矢量运动的电子无法返回南极，这表明面积定理不再适用. 在激光作用下，光极化变得扭曲，这导致了在反对称介质中的三次谐波发射将更加复杂. 另外, 国1(b)和(d)分别给出了脉冲面各为2π和4π对应的反转粒子数随时间的变化.

图1 (a) 当Θ=2π时，布洛赫矢量的运动轨迹, (b) 当Θ=2π时，反转粒子数随时间的变化, (c) 当Θ=4π时，布洛赫矢量的运动轨迹, (d) 当Θ=4π时，反转粒子数随时间的变化.Fig. 1 (a) The motion trajectory of Bloch vector, Θ=2π, (b) the evolution of population inversion w, Θ=2π, (c)the trajectory of Bloch vector, Θ=4π, (d) the evolution of population inversion w, Θ=4π.

Mücke等人[13]从实验和理论研究了载波拉比振荡对半导体GaAs谐波发射的影响，研究发现，在低强度激光驱动下，三次谐波仅展现出共振加强现象, 对于较高的强度，由于载波拉比振荡，三次谐波会发生明显的分裂. 在强场驱动下，Frasca等人[14]在两能级体系中观察到了拉比振荡. Hughes等人[15]研究发现载波拉比振荡与面积定理的失效有关. Rotter等人[16]用两能级模型研究发现在特定情况下会出现载波拉比振荡现象. 最近，Ciappina等人[17]发现钾原子谐波谱中也会出现载波拉比振荡，且三次谐波有着复杂的结构，但对其它碱金属原子谐波谱中是否普遍存在载波拉比振荡现象未做深入研究.

本文通过数值求解三维含时薛定谔方程，对铷原子在ω=E5p-E5s共振激光及非共振激光驱动下的三次谐波发射特性进行了研究. 结果表明，铷原子谐波谱中也存在载波拉比振荡现象，这一研究有助于理解铷原子在拉比振荡及载波拉比振荡机制下的谐波发射特征.

2 理论方法

在偶极近似和长度规范下，铷原子与激光场相互作用的含时薛定谔方程为(除特别说明外，均采用原子单位)：

(1)

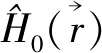
(2)

a2rexp(-a3r)]

(3)

(4)

E(t)为激光的电场强度，本文采用sin2包络，激光持续时间为20个光学周期，载波包络相位Ф=0. 激光波长分别选取ω=E5p-E5s的共振波长(794.9 nm)和非共振波长(1100 nm).

采用含时伪谱法[19]对波函数进行时间演化：

(5)

通过Ehrenfest定理，可得到与时间有关的偶极加速度为：

(6)

通过对偶极加速度进行傅里叶变换，可得到谐波的强度为：

(7)

3 结果与讨论

在计算时，我们选取了一个精确的模型势[20]，从表一可以看到，这种模型势得到束缚态能量和NIST数据库[21]给出的结果符合得很好. 此外，铷原子5s→5p之间的跃迁偶极矩阵元的计算结果与实验值[22]符合得较好.

表1 第一行和第二行分别为铷原子基态和第一激发态的束缚能, 第三行为跃迁偶极矩阵元.

图2 共振场(λ=794.9 nm)下铷原子谐波谱: (a) I=2.8×1011 W/cm2, (b) I=4.8×1011 W/cm2, (c) I=8.2×1011 W/cm2, (d) I=1.0×1012 W/cm2, 插图为三次谐波的放大图; 非共振场(λ=1100 nm)下铷原子谐波谱: (e) I=2.2×1011W/cm2, (f) I=3.2×1011 W/cm2, (g) I=5.0×1011 W/cm2, (h) I=6.6×1011 W/cm2.Fig. 2 The harmonic spectrums of rubidium atoms under the resonance field (λ=794.9 nm) are as follows: (a) I=2.8×1011 W/cm2,(b) I=4.8×1011 W/cm2, (c) I=8.2×1011 W/cm2, (d) I=1.0×1012 W/cm2. The insets are enlarged view of the third harmonic; the harmonic spectrums of rubidium atoms under the non-resonant field (λ=1100 nm) are: (e) I=2.2×1011 W/cm2, (f) I=3.2×1011 W/cm2, (g) I=5.0×1011 W/cm2, (h) I=6.6×1011 W/cm2.

图2为我们计算的谐波谱，在计算过程中，我们分别选取了四种脉冲面积：Θ≈2π，Θ≈3π，Θ≈4π和Θ≈5π (Θ≈dE0Δt，其中，d为铷原子5s-5p的偶极跃迁矩阵元，E0为激光电场峰值振幅,Δt为激光脉冲的半高全宽). 首先考虑激光波长为ω=E5p-E5s的共振波长(λ=794.9 nm)，从图2(a) (Θ=2.2π≈2π, I=2.8×1011W/cm2)可以看到铷原子发射的三次谐波呈现了一个正常的峰值，即三次谐波的发射效率最大.从图2(b) (Θ=2.9π≈3π,I=4.8×1011W/cm2)、图2(c) (Θ=3.8π≈4π,I=8.2×1011W/cm2)和图2(d) (Θ=4.9π≈5π,I=1.0×1012W/cm2)中看出，随着脉冲面积的增加铷原子三次谐波的结构发生了显著的变化，即分裂和加宽. 当激光波长为铷原子5s→5p的非共振波长(λ=1100 nm)时，我们发现随着脉冲面积的增大，铷原子发射的三次谐波展示出正常的峰值结构，如图2(e) (Θ=2.7π≈2π, I=2.2×1011W/cm2)、图2(f) (Θ=3.3π≈3π, I=3.2×1011W/cm2)、图2(g) (Θ=4π, I=5.0×1011W/cm2)和图2(h) (Θ=4.8π≈5π, I=6.6×1011W/cm2)所示. 在共振波长下，铷原子三次谐波表现出的复杂结构与Hughes等人[15]的结论一致，即在一个两能级共振体系中，当脉冲面积明显的超过2π时，会出现载波拉比振荡，这表明了面积定理的破坏.

图3 与图2一一对应的基态含时布居(黑色实线)、激发态含时布居(黑色划线)和激光场(红色实线). 激光参数与图2相同.Fig. 3 Time-dependent populations of the ground state (black solid) and excited state (black dashed) and laser fields (red solid) corresponding toFig. 2, respectively. The laser parameters are the same asFig. 2.

为了更好地理解三次谐波的复杂结构，我们对两态(5s和5p)布居分布进行分析. 图3(a)展示了Θ=2.2π≈2π (I=2.8×1011W/cm2，λ=794.9 nm)下的5s和5p态布居，可以看到激光脉冲结束时，5s态布居几乎完全耗尽(这对应于布洛赫矢量从南极螺旋上升到北极的行为)，而5p态布居接近于1，这种现象表明，在共振情况下的拉比振荡，铷原子发射的三次谐波呈现出正常的峰值结构[如图2 (a)]. 而在图 3(b) (Θ=2.9π≈3π，I=4.8×1011W/cm2，λ=794.9 nm)、图3(c) (Θ=3.8π≈4π，I=8.2×1011W/cm2，λ=794.9 nm)和图3(d) (Θ=4.9π≈5π，I=1×1012W/cm2，λ=794.9 nm)中可以看出，随着脉冲面积的增大，出现了类似于载波拉比振荡的行为，因此三次谐波出现了复杂的结构[如图2(b)-(d)].在非共振场下，可以看出，随着激光脉冲的结束,5s态布居分布没有耗尽，并且5s态布居和5p态布居不存在周期性振荡[如图3(e)-图3(h)]，这导致三次谐波呈现出正常的峰值结构[如图2(e)-(h)].

图 4 (a) 铷原子在共振场下的不同载波包络相位的谐波谱, 激光参数与图2(b))相同, (b) 铷原子在非共振场下的不同载波包络相位的谐波谱, 激光参数与图2(f)相同.Fig. 4 (a) Harmonic spectrums of different carrier envelope phases of rubidium atoms in resonance field, laser parameters are the same as those inFig. 2(b). (b) Harmonic spectra of different carrier envelope phases of rubidium atoms under the non-resonant field, laser parameters are the same as those inFig. 2(f).

少周期激光的载波包络相位会影响原子谐波发射强度及截止位置，而在长周期激光驱动下，载波包络相位效应将变得不再敏感. 本文基于载波拉比振荡机制下的铷原子三次谐波发射，研究了一种判定长脉冲驱动下的载波包络相位的方法.图4(a)和图4(b) 分别展示了共振波长(Θ=2.9π≈3π，I=4.8×1011W/cm2)及非共振波长下 (Θ=3.3π≈3π，I=3.2×1011W/cm2)的谐波谱，可以看到，共振波长激光驱动下，三次谐波结构会随着载波包络相位的改变而变化，而在非共振波长激光驱动下，三次谐波结构基本没有改变. 因此，利用低次谐波中的载波拉比振荡，可以确定长周期激光的载波包络相位.

4 总 结

本文通过数值求解三维含时薛定谔方程，研究了铷原子在ω=E5p-E5s共振激光及非共振激光驱动下的三次谐波发射特性，研究结果表明，在共振波长驱动下，脉冲面积会影响三次谐波的结构，这主要源于拉比振荡和载波拉比振荡机制的不同，在非共振波长驱动下，三次谐波呈现出正常的峰值结构，脉冲面积并不会影响三次谐波的结构. 通过研究长周期激光的载波包络相位对三次谐波发射的影响，可以发现，载波拉比振荡机制下，三次谐波结构会随着载波包络相位的改变而变化，因此，低次谐波中的载波拉比振荡可以作为确定长周期激光的载波包络相位的方案.