基于反应谱衰减关系和理想化反应谱模型的我国规范谱长周期段研究

聂利英，冯江江，林浩然，王 康，汪基伟

（河海大学土木与交通学院，江苏南京 210098）

引言

在规范谱的相关参数中，《中国地震动参数区划图》［1］GB 18306-2015（以下简称“《参数区划图》2015版”）中，6.1、7.1、8.2相关规定表明，Ⅱ类场地下基本地震动峰值加速度分区值、基本地震动加速度反应谱特征周期分区值和反应谱特征周期调整表的规定为强制执行，其他规定则是建议执行。这意味着反应谱长周期下降段各行业抗震规范可根据自身需要决定。

事实上，在我国各行业抗震规范中反应谱长周期下降段的规定呈现较强的多样性［2-7］。有的规范长周期下降段是单段下降函数［2-5］，有的是双段下降函数［6-7］，而且不同规范的下降函数指数也不相同。而且，我国规范谱长周期部分的规定偏重使反应谱分析得到的结构地震响应偏安全。例如《公路桥梁抗震设计规范》［2］JTG/T 2231-01-2020（以下简称“《公路桥梁抗震规范》”）的5.2.1的条文说明中指出：规范设计反应谱按T-1的速率下降是有足够安全保障的，没有必要再规定一段T-2的下降段；我国《建筑抗震设计规范》［6］GB 50011-2010（以下简称“《建筑抗震规范》”）长周期下降段采用双段下降函数的形式，文献［8］认为“其下降段第二段函数采用斜率为0.02的直线段，相对于欧美规范，我国的《建筑抗震规范》规范谱长周期下降段的取值是偏于保守的”。在我国规范中，最保守的是《水电工程水工建筑物工抗震设计规范》［3］NB 35047-2015，其下降段为单段下降函数、下降段衰减指数为0.6，远高于其他规范［2，4-7］。

与我国各行业反应谱长周期下降段规定呈现强的多样性相比，欧美规范谱长周期下降段规定的形式统一，均为双段下降函数，且衰减指数均为1、2（见表1）。这是因为欧美规范谱均是围绕理想化反应谱模型确定，其衰减指数1、2直接由理想化反应谱模型的定义决定（见图1）。因此，在欧美规范谱长周期下降段规定中，只需确定第二特征周期值TD参数，即可清晰的确定下降段函数。

图1 理想化反应谱模型中伪加速度谱、伪速度谱、位移谱的关系图Fig.1 Response spectrum relations among PSA、PSV and RSD in idealized response spectrum model

规范谱长周期下降段的研究与地震动记录统计得到的位移谱形态密切相关。基于实测地震动记录统计的反应谱研究，主要是地震工程领域关于地震动反应谱衰减关系的研究。目前我国缺少足够的地震动记录，在我国《参数区划图》2015版反应谱相关参数的统计研究中，其选取的3 896条水平向地震动来自于NGA数据库，另外选取的112条和62条来自于汶川地震和芦山地震［9］。来自NGA数据库的地震动数据占95%。美国NGA数据库于2013年发布更新后的地震动数据库，共包含607次地震中的21 539条地震动数据［10］，并利用该地震动数据统计回归了5个地震动反应谱衰 减 关 系：ASK 14［11］，BSSA 14［12］，CB 14［13］，CY 14［14］以及I 14［15］。因此，基于NGA数据库中的反应谱衰减关系，可对我国规范谱长周期下降段研究提供较强的支撑作用。

以理想化反应谱模型为我国规范谱模型进行研究时，其长周期下降段由TD确定。已有研究中TD计算公式主要分为2大类（见表2）：基于位移反应谱与伪速度反应谱的最大值RSDmax与PSVmax计算TD、基于地震动记录的峰值速度PGV和峰值位移PGD计算TD。其中基于反应谱求取TD的公式直接来源于理想化反应谱模型关于TD的定义，具有概念直观、清晰的特点。已有研究表明，TD参数与震级密切相关［16-20］，美国的NEHRP-2003规范［21］和FEMA-2012［22］规范提供了TD随震级的变化关系式（见表1）。目前，我国《参数区划图》2015版［1］以Ⅱ类场地地震动峰值加速度分区值表达50年10%超越概率下我国各地的地震强度（为强制执行，因此各行业规范均相同）。

表1 欧美抗震规范伪加速度反应谱下降段Table 1 The decline sections of pseudo acceleration response spectrum in European and American seismic codes

表2 T D计算公式Table 2 The calculating formulas of T D

我国规范谱长周期下降段研究常常包含在规范谱的总体研究中［8，23-27］。我国规范谱的研究一般是先设定规范谱谱型函数，然后以大量的地震动记录统计回归谱型函数参数［8，23-27］；其中的规范谱谱型函数，长周期下降段有单段函数也有双段函数，双段函数中下降段指数选取多样。在这些研究中，理想化反应谱模型的长周期下降段也是常用的规范谱谱型函数［25-27］；其中，耿淑伟等［25］的规范谱谱型函数中T2即是Tg，T3即是TD；方小丹［26］以5Tg为TD；周靖［27］则直接采用理想化反应谱模型。耿淑伟等［25］研究重点是对双段下降函数（T-1和T-2）和单段下降函数（T-1）进行比较；方小丹［26］研究中TD参考《建筑抗震规范》［6］选取为5Tg；周靖［27］研究中关于TD的研究最详尽，给出随着场地类别变化的TD。目前，尚无TD随着我国场地类别与地震动峰值加速度分区值变化的研究。

地震动反应谱衰减关系是关于反应谱谱值与震级、距离、Vs30（地下30 m深度范围内的平均剪切波速）等因素的变化规律函数。当基于NGA数据库的地震动反应谱衰减关系、以理想化反应谱模型为规范谱模型进行长周期下降段的研究时，地震动反应谱衰减关系可以提供统计意义上位移谱形态、提供TD计算所需反应谱谱值、建立我国地震动峰值加速度分区值与震级、距离和场地条件等因素的关系；由此则可得到在我国规范参数设定框架下的TD，以便为我国规范谱长周期下降段的研究提供参照。

文中主要研究内容如下：（1）通过阐明理想化反应谱模型，明确欧美规范谱长周期下降段的衰减指数1、2直接由理想化反应谱模型的定义决定；归纳现有研究中TD主要计算公式，并指出TD的计算与位移谱形态、反应谱最大周期、“结构所需周期范围”有关；（2）选择NGA数据库中与我国规范考虑因素吻合性最好的BSSA 14公式作为地震动反应谱衰减关系，基于BSSA 14分析探讨了位移谱形态类别、“结构所需周期范围”引起的位移反应谱谱值截取周期Tcut取值不同会直接导致TD不同的概念、以及位移谱形态类别的分布在Tcut不同取值下随震级、距离和场地类别的变化；（3）依据地震动衰减关系BSSA 14，考虑“结构所需周期范围”，得到以我国规范场地类别、地震动峰值加速度分区值为参照的TD值。

1 理想化反应谱模型及T D计算公式

欧美规范谱是围绕理想化反应谱模型［17］（见图1）而确定。图中PSA（pseudo-spectral acceleration）、PSV（pseudo-spectral velocity）、RSD（response spectral displacement）分别为伪加速度谱、伪速度谱、位移谱的谱值；T0、Tg、TD分别为伪加速度谱、伪速度谱以及位移谱平台段起始周期值，其中Tg、TD也被称为第一特征周期和第二特征周期［17］；T0～Tg、Tg～TD、TD以后的周期范围，分别为加速度、速度、位移敏感区。

位移谱、伪速度谱和伪加速度谱包含的信息完全相同，三者之间可相互转换，见式（1）：

式中：PSA、PSV、RSD分别是伪加速度谱值、伪速度谱值和位移谱值；ωn是无阻尼频率。由图1和式（1）可知Tg=2πPSVmax/PSAmax、TD=2πRSDmax/PSVmax。

由以上论述可见：理想化反应谱模型中，伪加速度谱下降段为双段下降函数，Tg～TD、TD以后下降段衰减指数分别为1、2两个确定值，且衰减指数是由理想化反应谱模型自身决定的。表1为美国的NEHRP-2003规范［21］、FEMA-2012规范［22］、美国ASCE/SEI 7-16规范［28］和欧洲的EC8-2004规范［29］中的反应谱下降段，均采用两段函数的形式，衰减指数为1、2。

在已有研究中TD的计算公式有多种，见表2。由表2可见TD的计算公式主要分为2大类：第1类是基于反应谱计算TD，如方法1、方法2；第2类是基于地震动记录的峰值速度PGV（peak ground velocity，PGV）和峰值位移PGD（peak ground displacement，PGD）计算TD，如方法3～方法6。

当位移谱周期足够长时，位移谱曲线的通常形态为随着周期逐渐增大位移谱值逐渐增大，达到最大谱值，然后趋于下降，最终稳定在地面最大位移PGD，且不再随着周期变化而变化［34-35］。表2中方法1、方法2为基于位移反应谱计算TD，二者皆是出于理想化反应谱对TD的概念定义，所不同的是位移反应谱谱值的截取周期Tcut不同，分别是“结构所需周期范围”5 s和反应谱最大周期10 s。由理想化反应谱模型定义可知，若围绕理想化反应谱模型求取TD，就需要取得周期足够长前提下位移谱中真正的最大位移RSDmax，而实际研究中此RSDmax的取值与位移谱形态、反应谱最大周期、“结构所需周期范围”有关。

2 T D与位移谱形态及T cut关联性

在地震工程领域，地震动反应谱衰减关系的研究为基于大量地震动记录统计分析建立的反应谱谱值与震级、距离、Vs30、地震类型等因素的函数关系。由地震动反应谱衰减关系可以直接观察到位移谱形态与震级、距离、场地类别的关系。

2.1 地震动衰减关系的选择及参数设置

2.1.1 地震动衰减关系的选择

目前我国缺少足够的地震动记录，在我国《参数区划图》2015版反应谱相关参数的统计研究中，来自NGA数据库的地震动记录占95%［9］，因此选取基于NGA数据库中的地震动衰减关系，以便对我国规范谱下降段参数研究提供较强的支撑。美国新一代地震动衰减关系研究计划NGA West2提供了5个地震动衰减关系：ASK 14［11］，BSSA 14［12］，CB 14［13］，CY 14［14］以及I 14［15］。这5个公式除了所考虑的震级、距离、场地类别等基本因素外，还考虑了断层机制、破裂方向性效应、上盘效应、盆地效应、场地非线性反应和余震等复杂因素。NGA所提供的5种地震动衰减关系的介绍及其适用范围见表3。

表3 5种地震动衰减关系及其适用范围简介Table 3 Brief introduction of five ground motion attenuation relationships with their application scope

我国《参数区划图》2015版的场地局部效应参数研究考虑了场地非线性和场地类别的影响［9］。由表3可以看出，仅ASK 14、BSSA 14包含了场地非线性影响，其中ASK 14考虑因素还包括上盘效应、破裂方向性效应、余震效应等我国规范中没有考虑的影响因素。由此看见BSSA 14地震动衰减关系与我国规范考虑的因素吻合性最好，因此本文选取BSSA 14作为地震动反应谱衰减关系。BSSA 14的函数表达式见式（2），

式中：Y是阻尼比为5%的伪加速度谱PSA（T；5%）（单位：g）或地面运动峰值加速度PGA（peak ground acceleration，单位：g）或地面运动峰值速度PGV（单位：cm/s）；FE为震级以及断层类型函数，M为震级，mech为断层类型；FP为路径函数，RJB（Joyner-Boore distance）为站点到地震破裂面地表投影的最近距离，region为地理区域；FS为场地函数，Vs30为地表以下30 m的平均剪切波速，z1为盆地深度（从地表到剪切波速为1.0 km/s土层的深度）；εn和σ为统计回归误差项。

由于我国规范没有考虑断层类型、盆地深度，而且在许多情况下盆地深度z1是未知的［12］，因此震级以及断层类型函数FE项中，当mech=0时，即是不区分断层类型的选项；场地函数FS项中，盆地深度z1采用默认值（z1=0），即不考虑盆地深度的影响；由于我国地域幅员辽阔，地理区域选用适用于全球范围（此时路径函数FP项中region=0）；统计回归误差项也不考虑，即εn与σ取0。因此，在对比分析中BSSA 14主要参数是震级、距离和Vs30。

2.1.2 震级、距离与Vs30参数

文中研究中的参数设置综合考虑了BSSA 14自身参数适用范围和我国规范的规定。BSSA 14的震级、距离适用范围分别是3.0～8.5级、0～400 km。我国《参数区划图》2015版是以Ⅱ类场地的地震动峰值加速度PGA的区间值amax（见表5）来标定地震动强度。周期为零时BSSA 14即为地震动峰值加速度衰减关系。文中设定震级范围为3.0～8.5级，步长为0.1级；考虑到BSSA 14公式的文献［12］显示距离0～4 km内实测地震动记录很稀疏，因此，距离取值范围为5～400 km，步长1 km。

BSSA 14的Vs30适用范围是150～1 500 km/s。中国与欧美国家的场地类别划分存在很大的不同，美国、欧洲和台湾等地区以Vs30为主要参数划分场地类别，我国场地类别划分涉及到3个参数：剪切波速为500 m/s的岩石定义界限、土层等效剪切波速Vse、场地覆盖土层厚度d。所以，结合我国规范利用BSSA 14进行研究时，需要选定与我国场地类别对应的Vs30。

我国与欧美场地的不同划分方式使得二者之间的对应性比较弱。文献［36］从我国场地类别定义的角度出发，基于BCV（bottom constant velocity，BCV）土层剪切波速分布模型，展示了二者之间薄弱的对应关系，以及我国各场地类别与其相邻场地类别的Vs30范围均出现严重交叉、重叠的现象，见表4。近年来关于Vs30预测公式的研究提供了多个以小于30 m土层深度的平均剪切波速计算Vs30的公式［37-39］。其中，Boore等［37］、Boore等［38］、Xie等［39］的公式为以单一深度z处的平均剪切波速推算Vs30的公式，可用于以我国场地类别推算Vs30。参考文献［36］关于我国不同场地的平均剪切波速和覆盖土层厚度的取值方式，以Boore等［37］、Boore等［38］、Xie等［39］的Vs30预测公式取代BCV模型，分析我国各场地类别的Vs30参数范围，同样可以看到类似的相邻场地范围Vs30范围的交叉、重叠现象，见表4。

Boore等［37］与Boore等［38］数据分别来源于美国加州、日本K-NET地区，其Vs30的覆盖范围为分别为150 m/s＜Vs30＜1000 m/s与120 m/s＜Vs30＜1500 m/s。而Xie等［39］数据来源于北京平原地区，其Vs30数据仅分布在160 m/s＜Vs30＜420 m/s，对我国Ⅱ、Ⅲ、Ⅳ类场地适用性较好，因此Xie等［39］公式计算仅针对我国Ⅱ、Ⅲ、Ⅳ类场。此外，周锡元［40］采用剪切波速500 m/s硬岩层埋置深度分别为50、80 m代表Ⅱ-Ⅲ、Ⅲ-Ⅳ分界线的平均剪切波速模型，得出Vs30与我国规范的对应关系；吕红山［41］、郭峰［42］利用美国几十个台站场地勘探资料、美国等国家和台湾地区的235个台站场地勘探资料，分别使用我国与美国的设计规范计算，提出Vs30与我国场地类别近似的对应关系。其研究也作为参考列于表4。

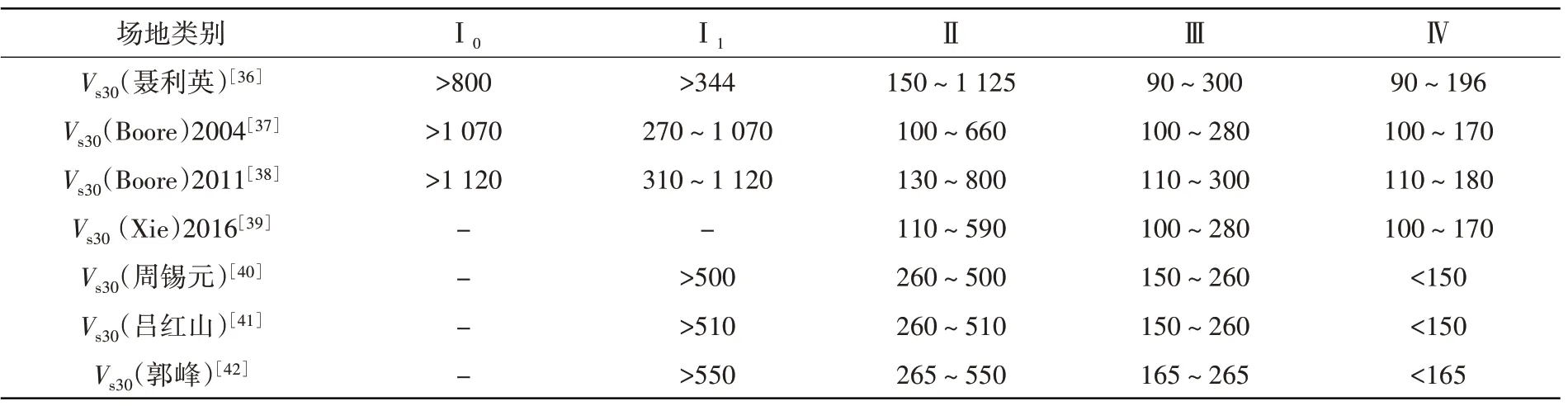
表4 不同学者给出的V s30与我国场地类别对应的关系Table 4 Relationships between V s30 and site categories in China has been given by different scholars m/s

由表4可见：各研究中Ⅲ类场地、Ⅳ场地对应Vs30范围都比较一致，因此设定其范围分别为180 m/s≤Vs30＜300 m/s、Vs30＜180 m/s；Ⅰ1场地与Ⅱ场地对应Vs30范围均比较广，且与相邻场地存在显著的交叉、重叠现象，因Ⅱ类场地是我国《参数区划图》2015版标定全国各地基本地震动峰值加速度与反应谱特征周期的场地，因此，以Ⅱ场地为主，为其设置较宽的Vs30范围，为300 m/s≤Vs30＜800 m/s；Ⅰ0～Ⅳ场地，总体上是场地地质越来越软，Vs30取值越来越小，为体现此特征，Ⅰ0场地、Ⅰ1场地对应Vs30范围设置为1 000 m/s≤Vs30、800 m/s≤Vs30＜1000 m/s。总体上，以1 000 m/s≤Vs30、800 m/s≤Vs30＜1 000 m/s、300 m/s≤Vs30＜800 m/s、180 m/s≤Vs30＜300 m/s、Vs30＜180 m/s为本文后续研究Ⅰ0～Ⅳ场地的Vs30范围，并且以Ⅰ0场地1 300、1 000 m/s；Ⅰ1场地950、800 m/s；Ⅱ场地750、600、450、300 m/s；Ⅲ类场地240、180 m/s；Ⅳ场地150 m/s为Vs30取值进行后续分析。

2.2 位移谱形态与T cut

BSSA 14是伪加速度谱衰减公式，可通过伪谱关系（见式（1））直接转化得到位移谱。BSSA 14公式周期适用范围是10 s，因此，位移谱周期范围为0～10 s。根据2.1节设定的参数范围，基于BSSA 14计算得到Ⅰ0～Ⅳ场地类别下的位移谱，并进行观察。通过观察可见，位移谱曲线可分为2种形态：第1种形态：位移谱最大值RSDmax在10 s内出现，达到最大值后下降，最后趋于稳定，如图2（a）所示；第2种形态，位移谱曲线在0～10 s周期内随周期的增加一直增大，如图2（b）所示。

当位移谱周期足够长时，位移谱曲线的通常形态为随着周期逐渐增大位移谱值逐渐增大，达到最大谱值，然后趋于下降，最终稳定在地面最大位移PGD，且不再随着周期变化［34-35］。第1种形态即是这种情况。但是，由于位移谱最大值RSDmax出现的周期随着震级的增加而增加，当在有限的周期范围内位移谱无法达到最大值时，就出现第2种形态。

由理想化反应谱模型定义可知，若要计算理想化反应谱模型定义中的TD，就需要取得周期足够长前提下位移谱中真正的最大位移谱值RSDmax。对于第1种情况，最大位移谱值RSDmax取值很明确，如图2（a）所示；对于第2种情况，RSDmax则为最长周期处的位移谱值，如图2（b）中B′所示。

图2 位移谱曲线形态以及T D取值示意图Fig.2 The curve shape types of displacement response spectrum and assigning T D value

表2中方法（1）是关于最大位移RSDmax取值需要考虑“结构所需要的周期”的研究。对于一般民用建筑结构，考虑延性设计后的周期需求范围为5 s［17，43-44］，若RSDmax取值周期很长，例如10 s，远超结构所需要的周期，则由图1理想化反应谱模型以及图2中TD取值方式可见：位移谱谱值截取周期Tcut取10 s定义的双线性位移谱O A′B′较Tcut取5 s定义的双线性位移谱O AB过于安全。这意味着，Tcut取10 s定义的双线性位移谱O A′B′与“结构所需周期范围”范围5 s内统计反应谱OB相比较，超越过多，因此Lumantarna［17］提出第2种位移谱形态下以“结构所需周期范围”为Tcut的取值方式。在图2（b）中，C和C′分别表示在第2种位移谱曲线形态中Tcut为5、10 s所计算的TD值。从图2（b）中可以看出，Tcut不同，TD值则不同。

Tcut不同，位移谱形态随着震级、距离、Vs30的分布也不同。基于BSSA 14分别以截取周期Tcut为5、10 s（即位移谱曲线最大周期分别为5、10 s时），展示位移谱曲线形态在不同震级、距离、场地类别下的分布情况。由于Ⅰ0、Ⅰ1类硬场地的位移谱曲线形态几乎均为第二类，因此，仅给出Vs30为450、240、150 m/s时的Ⅱ～Ⅳ类场地Tcut为5、10 s时位移谱曲线形态类别随着震级（4.5～8.5）、距离（5～50 km步长5 km）的分布状况图，见图3。

图3 不同场地类别、距离、震级下位移谱形态分布图Fig.3 The distribution of curve shape types of displacement response spectrum varying with site classifications，distances and magnitudes

由图3可知位移谱形态分布与Tcut相关：（1）Tcut取值越小，第2种位移谱形态越多，Tcut取5 s时，Ⅲ、Ⅳ类场地绝大部分是第2种形态；（2）Tcut取5 s时，位移谱曲线形态与距离、震级和场地类别均相关，场地越软、震级越小、距离越小时，第1种位移谱形态占比越大；场地越硬、震级越大、距离越大时，第2种位移谱形态占比越大；（3）Tcut取10 s时，位移谱曲线形态受距离影响较小，其分布主要与震级和场地类别相关；场地较软或震级较小时，位移谱曲线主要呈现第1种形态；场地硬或震级大时，位移谱主要呈现第2种形态。

3 基于我国规范参数设定的T D

TD参数与震级密切相关［16-20］，我国规范以地震动峰值加速度amax分区值表达期望的场地地震强度，因此需要建立以我国地震动峰值加速度分区值为参考坐标的TD参数。

在BSSA 14地震动衰减关系中，周期为零时的BSSA 14公式即为地震动峰值加速度PGA衰减关系。基于此，可以建立《参数区划图》2015版Ⅱ类场地地震动峰值加速度分区值amax与BSSA 14中震级、距离的分布关系，进而求得以我国地震动峰值加速度分区值amax为参考坐标的TD参数。具体过程如下：（1）当Vs30确定时，周期为零时BSSA 14即为PGA地震动衰减关系，其为震级、距离的函数。因此，首先确定Ⅱ类场地对应的Vs30，以表5的Ⅱ类场分区值amax对应的地震峰值加速度PGA范围，确定各分区值所对应的震级、距离的组合。例如，以Ⅱ类Vs30=450 m/s时表5中分区值0.05 g（其PGA范围0.04 g≤PGA＜0.09 g）为例：震级范围3.0～8.5级、步长0.1级取值；距离取值范围为5～400 km，步长1 km，利用BSSA 14地震动衰减关系计算PGA；使PGA值在0.04 g≤PGA＜0.09 g范围内的震级和距离组合共1 830组；此1 830组即为TD计算中分区值为0.05 g对应的震级、距离组合。其中，最小距离5 km对应的最小震级为4.5级；最大震级8.5对应的最长距离为194 km；（2）确定其他场地类别对应的Vs30，以《参数区划图》2015版中的场地地震动峰值加速度调整系数乘以表5中Ⅱ类场分区值amax及其对应的Ⅱ类场地峰值加速度的范围，得到与Ⅱ类场对应的其他各类场地加速度分区值及场地峰值加速度范围，按照（1）中方法，计算各自的震级、距离组合，例表5中Ⅲ类场Vs30=240 m/s时震级、距离组合数；（3）以BSSA 14计算各震级、距离组合下的TD，取算术平均值，作为以分区值区间对应TD。我国《建筑抗震规范》［6］的规范谱最长周期6 s，《公路桥梁抗震规范》［2］的规范谱最长周期10 s，对于一般民用建筑结构，考虑延性设计后的周期需求范围为5 s［17，43-44］，5 s是10 s的一半；相比于6 s，与10 s对比性更强，因此，文中分别取Tcut为5、10 s时计算的各类场地Vs30下TD，见表6。

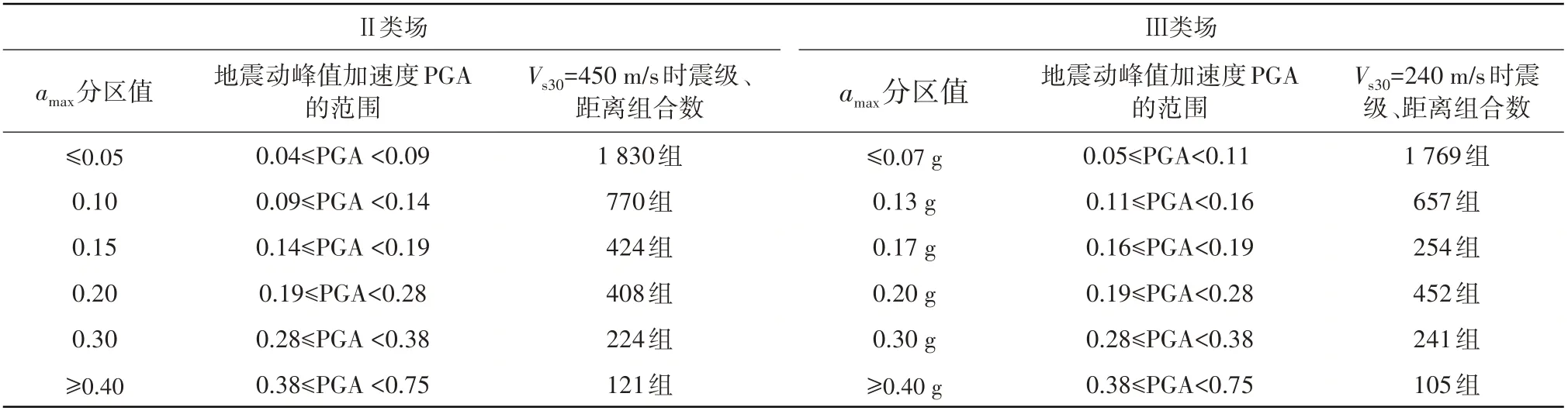
表5 地震动峰值加速度分区对应的峰值加速度的范围Table 5 The seismic peak ground acceleration range of its partition value g

表6 T cut为5 s和10 s时各类场地V s30下T DTable 6 The T D value of all class sites varying with V s30 when T cut is 5 s and 10 s

观察表6可知：（1）Tcut取值对TD有重要影响，Tcut取10 s时TD值均较取5 s时大；（2）Tcut取5 s时，在分区值0.05 g、0.3 g时，TD值总体上随着Vs30值的增大而增大，在分区值0.10～0.2 g、0.4 g时，TD值变化不大，Vs30增大对TD的影响基本上在10%之内；Tcut取10 s时，TD随着Vs30值的增大持续增大；（3）TD总体上随分区值的增大而增大，在Tcut取10 s时更显著一些，但是并不是单一的随着分区值的增大而增大，例如TD值在分区值为0.3 g时部分数据小于分区值为0.2 g时。

已有研究表明，TD参数与震级密切相关［16-20］。表1中美国的NEHRP-2003规范［21］、FEMA-2012规范［22］给出的TD与震级呈指数关系。在已知Vs30下，由BSSA 14得到的TD与震级、距离的关系显示TD对距离不敏感，随着震级单调增大，如图4（a）中以Vs30为450 m/s为例时所示。分区值的物理概念是某一PGA范围的代表值，PGA受距离与震级影响均很大，如图4（b）所示，因此当以分区值为参照给出TD时，没有像震级那样呈现随震级的增大而单一增大的显著规律。

此外，在图4（a）中7.2级前TD基本也是与震级呈现指数关系，但是其后出现了弱化现象，这是由于Ⅱ类场地7.0级后位移谱曲线形态大量为第二类的缘故，见图3（a）。在图4（b）中PGA随各个震级、距离的变化曲线在震级为5.5时出现不连续的情况，这是由于BSSA 14［12］中震级与断层类型函数FE为分段函数，当周期为零作为PGA衰减关系时，震级大于等于5.5级和小于5.5级分别用了两个函数的缘故。

图4 V s30=450 m/s时T D与PGA与震级、距离的关系图Fig.4 Relationship curves of T D varying with distances and magnitudes when V s30=450 m/s

4 存在问题与展望

基于位移反应谱求取TD（表2中方法1～2）是直接依据理想化反应谱模型中TD的定义，具有概念清晰明了的优势。以地震动记录求取TD（表2中方法3～6），概念则没有这样清晰，例如其地面最大位移PGD是地震动记录对应的位移反应谱中周期足够长时的等于地面最大位移的谱值，而不是RSDmax的概念。

文中基于地震动衰减关系研究基于理想化反应谱模型的TD取值问题，可以直观的看到位移谱形态类别及其随Tcut取值不同而引起的随震级、距离、场地的分布变化；也可以直观的看到Tcut选取不同TD则不同；同时，也便于理解基于理想化反应谱模型下“结构所需周期范围”与反应谱下降段安全程度的相关性。这也给出提示，若基于理想化反应谱模型研究规范谱长周期下降段，由于“结构所需周期范围”差异大，不同行业存在设置不同TD的需要。

在现阶段我国缺少足够的地震动记录、相关规范参数研究大量借用NGA数据库中地震动记录的前提下，基于NGA数据库中的地震动衰减关系，可对我国规范谱下降段参数研究提供较强的支撑作用。因为地震动预测模型是具有区域适用性的，地震动区域特征，例如场地、路径效应存在很强区域依赖性，而NGA数据库中的反应谱预测模型并不能完全体现我国的区域性特征。因此在未来，随着我国地震动记录的逐步积累丰富，需要发展出基于我国的地震动记录的地震动衰减关系。

在Vs30参数设置过程中，各研究中Ⅲ类场地、Ⅳ场地对应Vs30范围都比较一致，因此Vs30范围设置比较可靠；考虑到我国《参数区划图》2015版标定全国各地基本地震动峰值加速度与反应谱特征周期的场地为Ⅱ类场地，因此Ⅱ类场地对应的Vs30被赋予较大的范围，以方便研究结论的可参考性。中国与欧美国家的场地类别划分的不同，使得我国各场地类别与相邻场地类别之间Vs30范围均出现严重的交叉、重叠现象，尤其是Ⅰ1场地与Ⅱ场地最为显著。此种前提下，Vs30范围设置以Ⅱ类场地为主，相对的，Ⅰ0场地、Ⅰ1场地对应的Vs30范围设置合理性和客观性偏弱。

由于各类场地Vs30范围设置问题，表6中Ⅰ0场地、Ⅰ1场地的TD数据精度的进一步提高，有待于Vs30与我国场地的对应关系清晰化的研究。Vs30参数广泛的应用在欧美国家的场地类别定义以及各类地震动衰减关系的研究中，如何建立我国的场地类别定义与Vs30清晰的换算关系，是一个很值得深入研究的问题。此问题的清晰化将会极大提升我国研究中借鉴国外研究成果的便利性。

5 结论

由理想化反应谱模型与欧美规范谱下降段的规定可见，TD为确定下降段函数的关键参数。基于NGA数据库的BSSA 14地震动反应谱衰减关系，直观的观察了位移谱形态种类、位移谱形态随Tcut取值不同而引起的随震级、距离、场地类别的变化、了解了考虑“结构所需周期范围”选定不同Tcut与长周期下降段安全程度的相关性，给出随我国设计地震动峰值加速度分区值变化的TD参数参考值。文中主要研究结论如下：

（1）基于BSSA 14计算出的位移反应谱，主要有2种位移谱曲线形态。Tcut不同，2种位移谱形态分布随震级、距离、场地类别的分布情况不同：1）Tcut取值越小，第2种位移谱形态越多，Tcut取5 s时，Ⅲ、Ⅳ类场地绝大部分是第2种形态；2）Tcut取5 s时，位移谱曲线形态与距离、震级和场地类别均相关，场地越软、震级越小、距离越小时，第1种位移谱形态占比越大；场地越硬、震级越大、距离越大时，第2种位移谱形态占比越大；3）Tcut取10 s时，位移谱曲线形态受距离影响较小，其分布主要与震级和场地类别相关；场地较软或震级较小时，位移谱曲线主要呈现第1种形态；场地硬或震级大时，位移谱主要呈现第2种形态。

（2）TD随着Tcut而变化，基于NGA数据库中地震动衰减关系BSSA 14，以及一般民用建筑结构考虑延性设计后的周期需求范围、桥梁抗震规范谱最长周期规定现状，给出Tcut取5、10 s时随设计地震动峰值加速度分区值变化的各类场地TD参考值。其他行业则需根据自身“结构所需周期范围”设定Tcut求取相应的TD。