非结构化与结构化网格剖分在地下水数值模拟中对比分析

张鹏伟 费宇红* 郝奇琛 李亚松 朱玉晨 孟素花 郭春艳

（1、中国地质科学院水文地质环境地质研究所，河北 石家庄 050061 2、福建省水循环与生态地质过程重点实验室，福建 厦门 361001）

地下水是重要的自然资源，作为许多地方工业、农业和居民生活主要水源或唯一供水水源，其水量与水质变化备受社会各界关注。地下水数值模拟是研究地下水流场变化、溶质运移和热量运移的重要方法，目前求解地下水模型的数值方法包括有限差分法(FDM)、有限元法 (FEM)、边界元法 (BEM) 和有限分析法(FAM)。MODFLOW 作为有限差分地下水流数值模型的代表，是目前水资源利用、环境保护等科研和生产领域最为普及的计算程序。空间离散化是构建地下水数值模型的重要步骤，MODFLOW 为其提供了结构化网格与非结构化网格两种剖分方式，为深入理解非结构化版本（MODFLOW-USG） 与 传 统 结 构 化 版 本 ( 包 括MODFLOW-2000，-2005，-NWT，-LGR) 的区别和特点，本文针对以上两种网格剖分方式从求解方法、连接方式以及单元格几何形状等方面进行分析对比。

1 求解方法

MODFLOW-USG 基于控制体积有限差分法（Control Volume Finite-difference, CVFD）进行非结构化网格剖分，该方法综合有限差分法和有限元法的优点，采用差分法进行离散，又采用不规则的网格形状处理模型边界和网格疏密的问题，从而保证了流场维度的灵活性[1]。对于单元n 与每一个与之相邻的单元m，控制体积有限差分方程的一般形式为[2]：

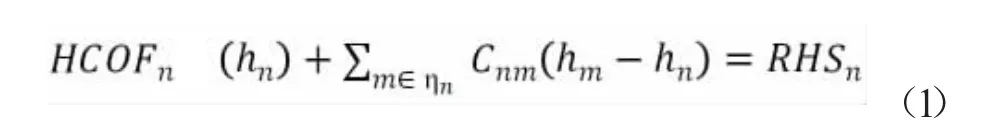
式中：Cnm为单元n 与相邻单元m 之间的系数；hm和hn分别为m 单元和n 单元的水头；HCOFn是所有与单元n 水头hn相关的系数项的总和；RHSn为所有常数项和已知项，也称平衡方程右侧项。

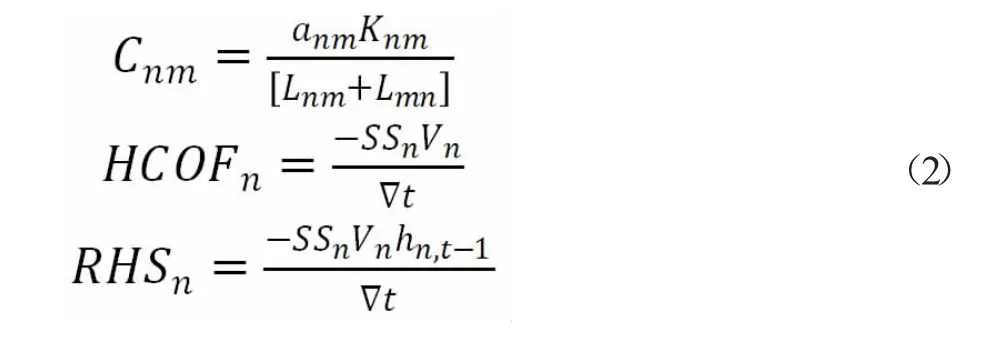
式中：anm是单元n 与单元m 公共面在垂直于流向方向上的投影面积；knm为单元n 与单元m 之间的渗透系数；Lnm、Lmn为单元n 和单元m 中心到公共面的垂直距离；Vn为单元n 的体积；SSn为单元的储水率；∇t 为时间步长；t-1 为上一时间步长。（图1）

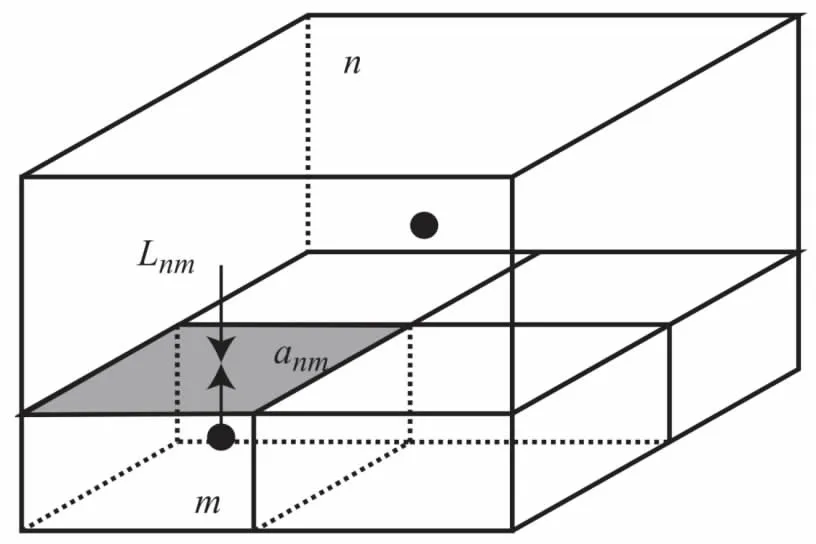
图1 非结构化网格空间离散示意图

传统结构化网格剖分所采用的有限差分方程同样是基于质量守恒和水量平衡方程构建，对于单元(i,j,k)与相邻单元(i,j-1,k)，二者间的流量计算方程如下[3]：

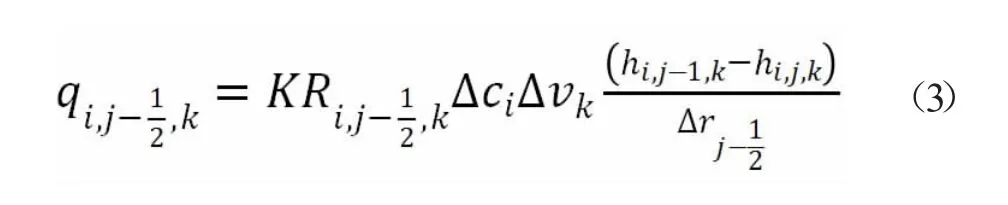
式中：hi,j,k是单元(i,j,k)的水头；qi,j-1/2,k是两相邻单元间的流量；Δci和Δvk分别为单元的宽和高；Δrj-1/2为两单元中心间距。对于单元(i,j,k)有限差分的一般计算方程为：

式中：KR、KC、KV 分别为沿j、i、k 方向的渗透系数；QSi,j,k为各类源汇项；SSi,j,k为单元储水率。（图2）

图2 结构化网格空间离散示意图

2 连接方式

结构化网格剖分是指每个内部单元格具有相同数量的毗邻单元，除了在边界处的单元以外，每个单元通常固定连接到6 个主方向上的相邻单元（图2）。这种连接方式使其具有网格生成速度快、数据结构简单的优点，同时方便数据和相关参数的准备，便于赋值，最重要的是计算稳定性好并且收敛速度快。然而在实际模拟过程中，结构化网格剖分存在明显的局限性：在刻画不规则边界时，需要将研究区以外的单元设置为不活动单元，且研究区边界往往容易形成锯齿形边界（图3 (b)）；若采用网格加密的方式细化边界或重点区域，加密区域行和列会扩展至模型域的边缘，从而产生许多非必要的计算单元，大大影响了模型的计算效率并且容易造成模型不收敛的问题。

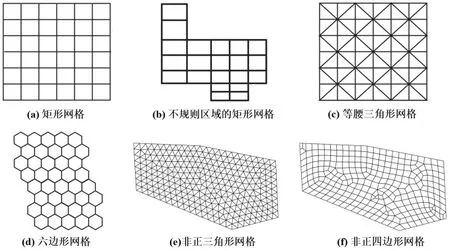
图3 结构化网格剖分方式

非结构化网格则是指对于所有单元来说，网格单元与相邻单元的连接数不是固定值，每一个单元可以与任意数量的网格相邻。如图4 所示，一个单元与周围单元的连通性取决于公共边（面）的数量，而每个单元的不尽相同，这就导致所列的方程组是非结构化的。非结构化网格允许定义不规则形状的模型域，在模型区域之外，不需要设置不活动单元。

图4 非结构化网格剖分方式

3 单元格几何形状

结构化网格剖分通常对模型进行正交矩形剖分，但以单元几何形状区分结构化与非结构剖分是常见的错误认知，需要注意的是规则三角形或六边形网格同样是结构化的，关键在于其每个单元具有相同数量的毗邻单元。对于结构化网格剖分，模型层必须在整个模型领域中保持连续，所有模型层中的单元数必须相同，这意味着需要插入完整的模型层，且必须在弱透水层尖灭区域设置最小厚度。结构化网格单元编号根据网格的行、列、层属性编号。

如图4 所示，非结构化网格剖分允许单独或组合使用嵌套网格、三角形、矩形或其他多边形形状的几何图形以适当地离散区域，从而有效提高河流和井等对象的模型分辨率。非结构化网格单元体必须是凸柱状体，且柱体侧面垂直于水平底面，但各层无需在整个模型区域保持连续，模型层厚度可设置为零。各层可独立离散化，比如对浅层河流处细化剖分，深层保持粗化网格。为方便预处理和后处理，MODFLOW-USG 保留了分层的概念，但单元格编号不显示分层信息，单元从上层开始编号，然后依次按网格层级顺序编号至最底层单元。

对于计算精度而言，标准的CVFD 方程要求连接相邻单元中心点的连线垂直于公共面，并且连线与公共面的交点应处于公共面的中心[4]。但嵌套网格、四叉树网格以及具有非正多边形网格可能会违背此要求，且偏离CVFD 法的要求越大，地下水流数值解的精度损失也就越大；然而增加细化网格的数量，提高模型分辨率又会提高模型精度，降低误差，二者之间的关系很难量化。有不少学者已通过理论推导以及模拟实验的方式已经证明，分辨率越高，模型对水位模拟的精度越高，并且相比较于细结构化的网格剖分，其计算时长也会大大降低[5-6]。

4 结论

总结来说，结构化网格剖分具有操作简便、生成速度快、数据结构简单等优点，但在研究重点区域加密、模拟不规则研究区边界以及模拟不连续弱透水层或地层尖灭等方面具有一定局限性。

非结构化网格剖分允许刻画不规则边界，支持局部加密，计算效率及计算精度更高，稳定性更强。