基于遗传算法的地下坑道暖通管线综合优化方法研究

苗文涛 吕 明

（华能山东电力设计有限公司，山东 烟台 264000）

地下坑道是人防工程中最为重要的组成部分，在其封闭的有限内部空间内需布置密集的暖通专业、给排水专业、电气专业等综合管线，管线尺寸与类型众多、空间布局难度大、设计和施工复杂、专业间协调工作量大，影响着综合管网的工程设计与施工养护[1-2]。由于暖通管线是综合管线布局系统工程中最为复杂的部分，它包含了通风空调管道（送风管、排风管、蒸汽管等）、热力管道（采暖管、热水管等）等，管道直径较大、附件多，它的布置和协调工作的优劣直接影响到整个系统工程的设计与实施。为避免暖通管线自身以及与其他各专业管线间在平面和立面上的交叉与冲突，以节省有限坑道空间、降低管线建造成本，同时为维修操作空间创造条件，降低管网布局不良造成整个系统工程中的浪费，研究暖通管线的综合优化方法受到诸多学者的重视，成为目前的研究热点[3]。

目前，关于暖通管线的优化布局问题有着众多的求解方法，郑轶丽[4]等人通过将其抽象为数学规划问题，同时在数学推导中加入了现实求解准则，提高了算法的运算能力；吉瑞博[5]等运用图论方法，以求解具有空间布局约束的全局最优解；王彦[6]等人应用人工视神经网络方法求解空间组合优化的旅行商问题；王烜[7]等借鉴了生物学理论采用遗传算法、人工蜂群算法和蚁群算法求解空间最优的不确定性搜索问题。

基于现有的文献研究，本文以地下坑道暖通管线的综合优化设计为研究对象，在给定的地下坑道尺寸的基础上，提出采用遗传算法的地下坑道暖通管线布局优化方案，以管线不发生面积重叠为目标函数，构建遗传个体的适应度函数以及交叉算子、变异算子，建立相应的数学分析模型进行数值计算，以求解地下坑道管线布局的全局最优解。

1 遗传算法的基本原理

遗传算法是美国学者John Holland 基于生物学规律提出的模拟生物进化中的染色体基因的交叉和变异等过程的数学模型，它是能够用于解决复杂的组合优化问题并得到全局最优解的鲁棒搜索算法。遗传算法的基本原理是将“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编码串联群体中，按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选，使适应度高的个体被保留下来，组成新的群体新的群体既继承了上一代的信息，又优于上一代这样周而复始，群体中个体适应度不断提高，直到满足一定的条件遗传算法的算法简单，可并行处理，并能得到全局最优解。

2 暖通管道综合优化遗传算法函数构建

2.1 目标函数与适应度函数

在暖通管道的平面布局中，其目标函数是管道间的平面面积无重叠，因此可以构建其目标函数为管道的重叠面积。

为使得两个管道间不冲突，即两者之间的重叠面积为零，假设任意两个圆形暖通管道的中点坐标分别为Pi（xi，yi）、Pj（xj，yj），管道直径分别为Di、Dj，因此根据几何关系，如果管线在几何上相互冲突，管道间在坐标x 方向上的交叉长度dx，管道间在坐标y 方向上的交叉长度dy，可以构建目标函数Sij如公式（1）所示

适应度函数是遗传算法进化过程的驱动力，也是进行自然选择的唯一标准，结合管道重叠问题的要求，实现对群体中个体的优胜劣汰操作，将个体的适应度控制在一定范围内，为此选择指数函数为暖通管道综合优化的适应度函数如公式（2）所示：

其中，Si为暖通管道的重叠面积大小，β 为适应性系数，表征重叠暖通管道个体与其他管道的适应度，数值越小适用性越差，f 为适应性函数。

2.2 交叉算子与变异算子

遗传算法中的交叉算法是模拟生物学中两个个体之间的染色体交换部分基因以形成新的个体。因此，可以假设两个个体xtA、xtB，进行交叉产生新个体、，的函数为

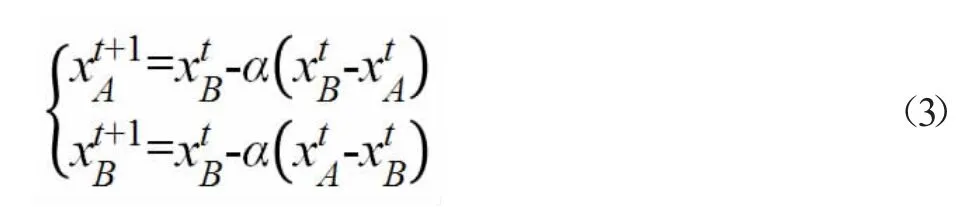
其中，α 为0～1 的随机数，t 为遗传进化代数。

实现个体基因的变异通过采用变异算子对基因值进行随机扰动，它产生新个体的辅助方法，决定了遗传算法的局部收缩能力，同时保持了种群的多样性。因此，构建管道布局的变异算子如公式（4）所示：

其中，Δ（t，Ukmax-xk）、Δ（t，xk-Ukmin）表示[0，xk-Ukmax]、[0，xk-Ukmin]范围内符合非均匀分布的一个随机数。

3 暖通管线综合优化布局建模及设计实现

3.1 计算算例

设给出地下坑道由1 个主坑道和3 个次坑道组成，3个次坑道编号分别为1#、2#、3#，由于主次坑道的断面尺寸不一致，坑道设计时将所有次坑道的直墙顶与主坑道的直墙顶设置在同一水平面上。坑道的断面尺寸如图1所示，主坑道拱部为半圆形，半径为r=250cm，侧墙为直墙面，墙面高为h=250cm，主坑道宽度为2r=500cm；1#次坑道拱部半径为r=100cm，侧墙高为h=100cm，主坑道宽度为2r=200cm；2#次坑道拱部半径为r=90cm，侧墙高为h=90cm，主坑道宽度为2r=180cm；3#次坑道拱部半径为r=80cm，侧墙高为h=80cm，主坑道宽度为2r=160cm。所有坑道内都依据设计的需要，排布4 种不同尺寸的暖通管道，分别为A 管、B 管、C 管和D 管。为计算方便，除暖通管道的直径大小不一外，所有坑道内的暖通管道的材质、类型等属性一致。为保证后期的维修空间，主次坑道管线间的距离均应大于200mm，所有管线均应分布在拱内，不侵入下部矩形空间。各坑道内的管线直径参数如表1 所示，表中管道直径均为包含管道保护层等附着物的外轮廓直径。计算时，选取圆形拱的中点为原点，水平向为x 轴，垂直向为y 轴。

表1 各个坑道内的暖通管线直径

图1 坑道的断面图及尺寸

3.2 暖通管线综合优化设计结果分析

以管线不发生面积重叠为目标函数，运用本文构建的适应度函数以及交叉算子、变异算子，如公式（3）～公式（4）所示，采用数学分析程序建立相应的数学仿真分析模型，经过1000 的基因进化代数计算，取得了稳健的遗传分析结果，具体各个坑道的暖通管线布局优化结果如图2 所示。从图中可以看出，仿真计算的坑道暖通管线布局准确合理，能够满足前文3.1 小节中的几何约束条件，没有出现管道交叉和面积重叠现象。

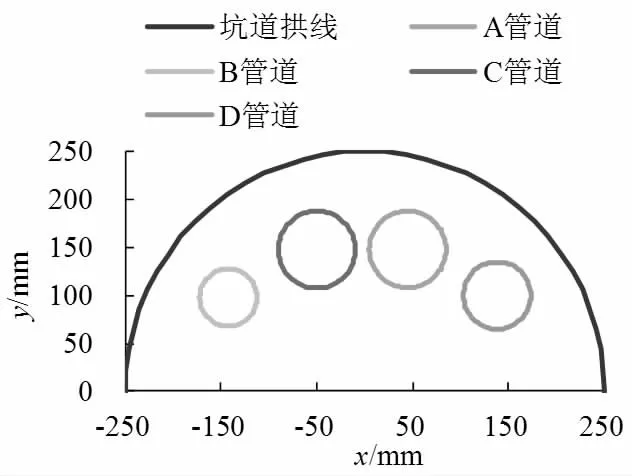
图2 主坑道暖通管线布局仿真结果

对仿真计算过程中，遗传个体的基因进化代数与适应度函数关系进行分析，结果如图3 所示。从图中可以看出，由于群体个数计算个体较少，个体间的基因差异大，在计算的开始阶段（基因进化代数小于30 代），遗传算法的计算速率加快，使得适应度的函数值取得了迅速提升，新个体的面积重叠可能性迅速降低，在这个阶段起主要作用的是交叉算子。基因进化代数大于30 代后，适应度的函数值则逐步区域稳定，各个新个体的差异逐渐趋同，限制了进化速率，此阶段起到主要作用的是变异算子。从基因进化代数大于90 代以后，适应度的函数值基本稳定在1.0，表明各个管线之间已经不存在面积重叠的现象，确定了管线布局的最优解。另一方面，采用遗传算法能够在较少的遗传代数条件下搜寻合理的地下坑道暖通管线的综合布局方式，大大降低了依赖人工经验的管网交叉和冲突调整工作量，提高地下坑道空间的利用率和暖通管网的铺设效率，将遗传算法解决管线的布局问题具有可行性和适用性。

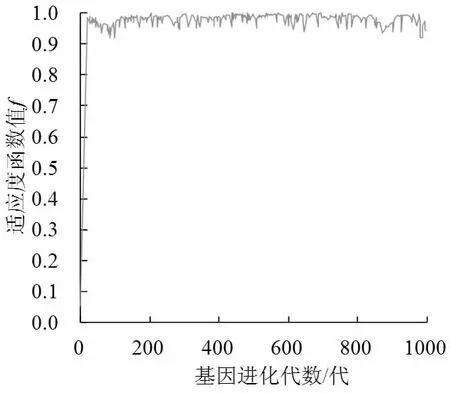
图3 遗传个体的基因进化代数与适应度函数关系曲线

4 结论

以地下坑道暖通管线的综合优化设计为研究对象，在给定的地下坑道尺寸的基础上，提出采用遗传算法求解地下坑道暖通管线布局优化方案，得到以下几个结论：

4.1 将遗传算法引入求解地下坑道管线布局的全局最优解具有应用创新型，本文基于遗传算法，以管线不发生面积重叠为目标函数，如公式（1）所示，构建了遗传个体的适应度函数以及交叉算子、变异算子，如公式（3）～公式（4）所示。

4.2 基于计算实例，建立相应的数学分析模型进行数值仿真计算，结果表明仿真计算的坑道暖通管线布局准确合理，能够满足设计的几何约束条件，没有出现管道交叉和面积重叠现象。

4.3 遗传算法仿真计算能够在较少的遗传代数条件下搜寻合理的地下坑道暖通管线的综合布局方式，大大降低了依赖人工经验的管网交叉和冲突调整工作量，将遗传算法解决管线的布局问题具有可行性和适用性。