高斯光束非球面整形系统整形特性研究

张子怡，陈 檬，王春磊，相贺鹏，陶锐卿

北京工业大学材料与制造学部激光工程研究院，北京 100124

1 引 言

激光独有的特性使其在众多领域都具有重大应用价值。而在激光加工、激光医疗等领域里，激光光强分布不均匀会导致局部温度过高从而破坏材料性能，因此将高斯光束整形为平顶光束可使激光更有效地应用到各个领域。目前激光光束整形一般使用孔径光阑[1]、非球面透镜[2]、衍射光学元件[3]、微透镜阵列[4]、液晶空间光调制器[5]等整形器件。在众多的整形方法中，非球面镜整形由于其结构简单、高损伤阈值、整形效率高被广泛使用。

1965 年，Frieden[6]首次提出利用非球面透镜组将高斯光束转化为平顶光束的方法，该方法主要根据能量守恒定律，在出射光线与入射光线之间建立映射函数，达到能量重新分配的效果。1969 年，Kreuzer[7]提出一种通用的求解整形系统面型参数的方法，并对这种设计方法申请了专利，此设计方法直到今天还在广泛使用，理论上来说，该系统可实现任意波前变换。2011 年，高瑀含[8]在该方法的基础上结合zemax 软件的宏语言(ZPL)功能实现了系统的自动优化，使非球面整形系统设计更加简单。

在使用非球面整形系统的过程中发现，对不同入射参数的高斯光束整形时，均会在整形镜后找到一个光束呈平顶分布的位置，本文称之为最佳整形位置，通过对不同入射光束直径和发散角的激光束整形，发现与之对应的最佳整形位置也会发生变化，并且平顶分布也会有所差异，因此本文重点探究入射光束光斑大小与发散角对非球面整形镜整形效果的影响，以及它们与最佳整形位置的关系，并通过建模快速得到最佳整形位置的方法。

2 实验准备

2.1 平顶分布均匀性评价方法

根据ISO 13694:2018 标准[9]中对平顶光束均匀性的描述，选择以下三种参数作为本文评价整形效果的方法。

平坦因子(Flatness factor，FF)用来描述平顶光束顶部平坦程度，当FF→1 表明分布趋于理想平顶分布，计算公式：

光束均匀性U(Beam uniformity)用来描述平顶光束顶部均匀性，当U→0 表明平顶分布的顶部越均匀，毛刺越少，计算公式：

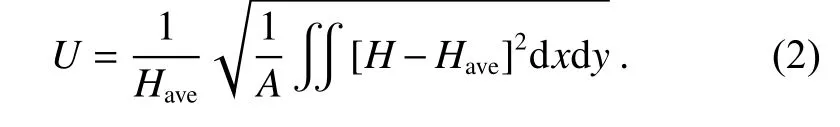
边缘陡度s(Edge steepness)用来描述平顶光束边缘轮廓，当s→0 表明分布的边缘趋近垂直，计算式如下：

公式中各物理量含义如图1 所示，本文 η为最大值的0.8 倍，ε为最大值的0.3 倍。

2.2 非球面整形系统的原理及结构

非球面整形设计的原理最初是在1965 年由Frieden[6]提出，简单描述就是将高斯光束整形为平顶光束的过程中，总能量不变的前提下进行能量的重新分配，即将高斯光束中间部分匀化到边缘，达到整形为平顶的效果，该过程中通过公式推导得到能量重新分配的映射关系，即入射光位置与出射光位置的对应关系，之后根据1969 年Kreuzer[7]提出的非球面面型参数的求解过程得到非球面整形结构。一直以来，非球面整形镜的设计均使用该原理，随着光学设计软件的发展和加工精度的提高，整形结构的设计越来越简便，整形结果也越来越好。

非球面整形系统一般由两片非球面透镜组成，第一片非球面引入波像差使高斯光束能量重新分布，第二片非球面补偿第一片产生的波像差并对出射光束进行准直。该系统分为两种，一种是伽利略型，一种是开普勒型。其中开普勒型非球面镜组中间会有聚焦，当输入光功率很大时，焦点处过强的峰值功率会将空气击穿，产生等离子体，损失能量，因此，该类型只适用于小功率激光器，而伽利略型非球面镜组不存在聚焦点，可适用于更大一些的功率。

2.3 整形镜设计参数及实验装置

实验所用非球面整形镜为伽利略型结构，是以波长1064 nm，入射光束束腰3 mm 的基模高斯光束进行设计的，其结构如图2 所示，设计参数如表1 所示。

为探究入射光斑大小与发散角对该整形镜整形效果的影响，使用图3 实验装置进行探究，该实验装置中通过改变聚焦透镜F 的焦距，达到改变发散角的目的；通过改变透镜F 与整形系统间的距离达到改变光斑大小的目的。其中，光源使用北京赢圣科技公司BAOSEC 1-IR 型号激光器，该激光器为1064 nm 皮秒固体激光器，其出射光功率稳定性好，便于实验，图4 为激光器测试一小时的功率变化图；CCD 使用DataRay 公司的WinCamD-LCM 型号进行光斑的探测，可通过DataRay 软件导出其光斑强度数据，从而进行平顶光束均匀性评价的计算。

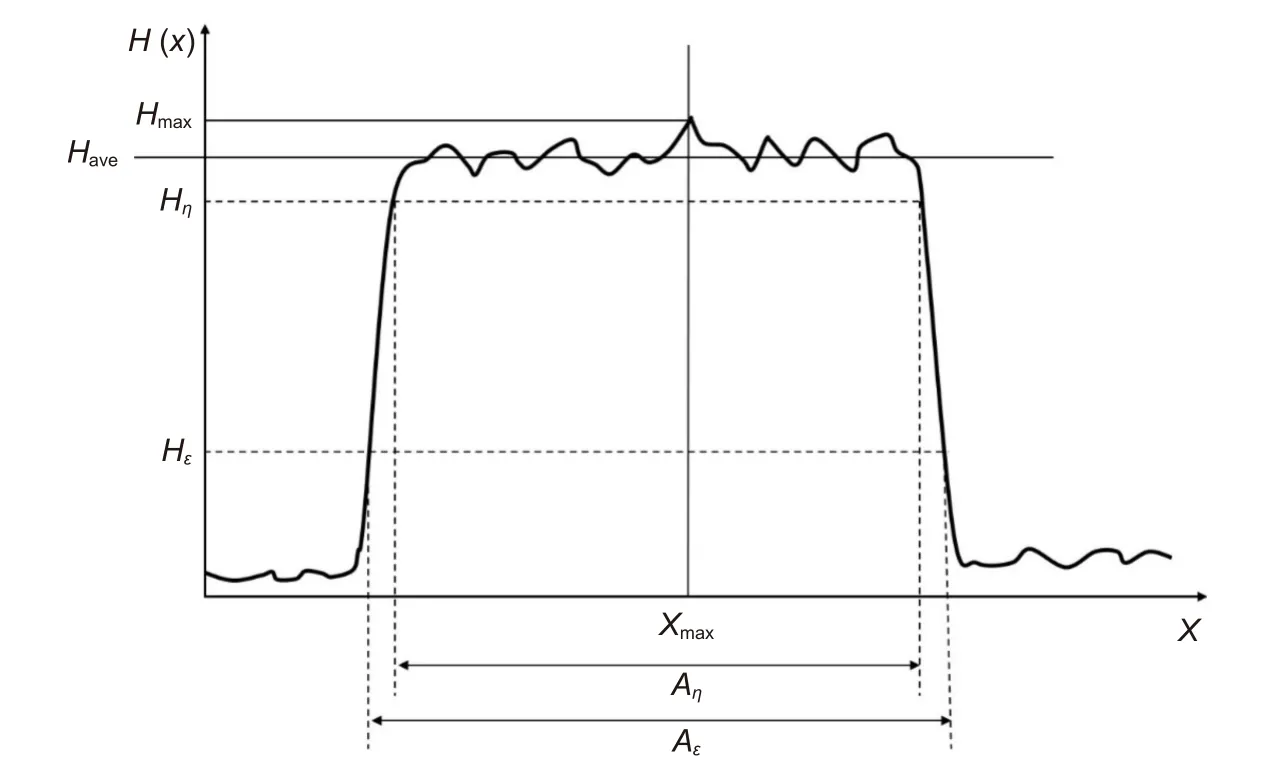
图1 二维坐标中能量密度分布图解Fig.1 Illustration for a uniform energy density distribution H(x) in one dimension

图2 非球面整形系统结构Fig.2 Structure of aspheric shaping system

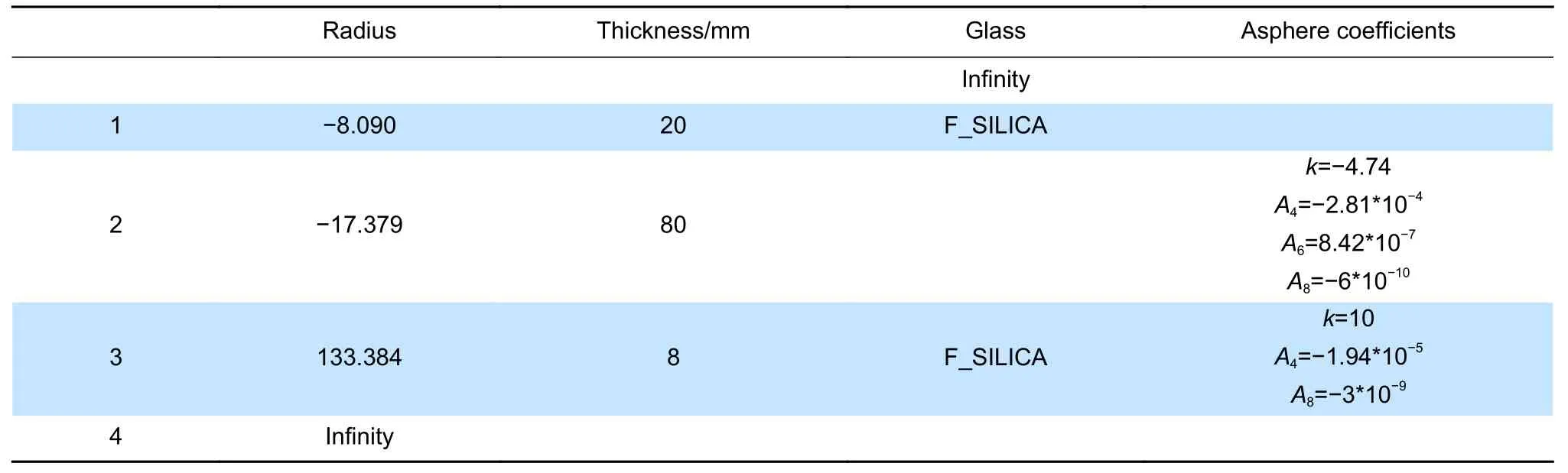
表1 非球面整形镜设计参数Table 1 Design parameters of aspheric shaping mirror

图3 实验装置图Fig.3 Experimental device diagram

图4 激光器功率稳定性测试Fig.4 Laser power stability test

3 单因素影响实验

3.1 入射光斑大小对整形效果的影响

使用如图3 装置，其中透镜F 的焦距为200 mm，根据发散角测量方法测得，经过透镜后的光束发散角为6.5 mrad，改变整形镜的位置，将入射光束直径从1.0 mm 开始逐渐变大，得到不同入射直径对应的整形最佳位置，以及该位置处的光强分布如图5，再经过数据处理得到其平坦因子、光束均匀性和边缘陡度，见表2 。

将表2 数据进行拟合，分别得到最佳整形位置、平坦因子、光束均匀性、边缘陡度与入射光束直径之间的关系，如图6。

实验发现随着入射光束直径增加，最佳整形位置越来越靠近整形镜，并且靠近速度逐渐减缓；光束均匀性与边缘陡度均是先变好再变差，存在最佳入射光束直径，通过计算拟合曲线最低点对应横坐标，得到光束均匀性最好的入射光束直径为1.49 mm，边缘陡度最小的入射光束直径为1.44 mm。但是研究发现入射光束直径对平坦因子没有明显的影响，平均分布在86%左右。

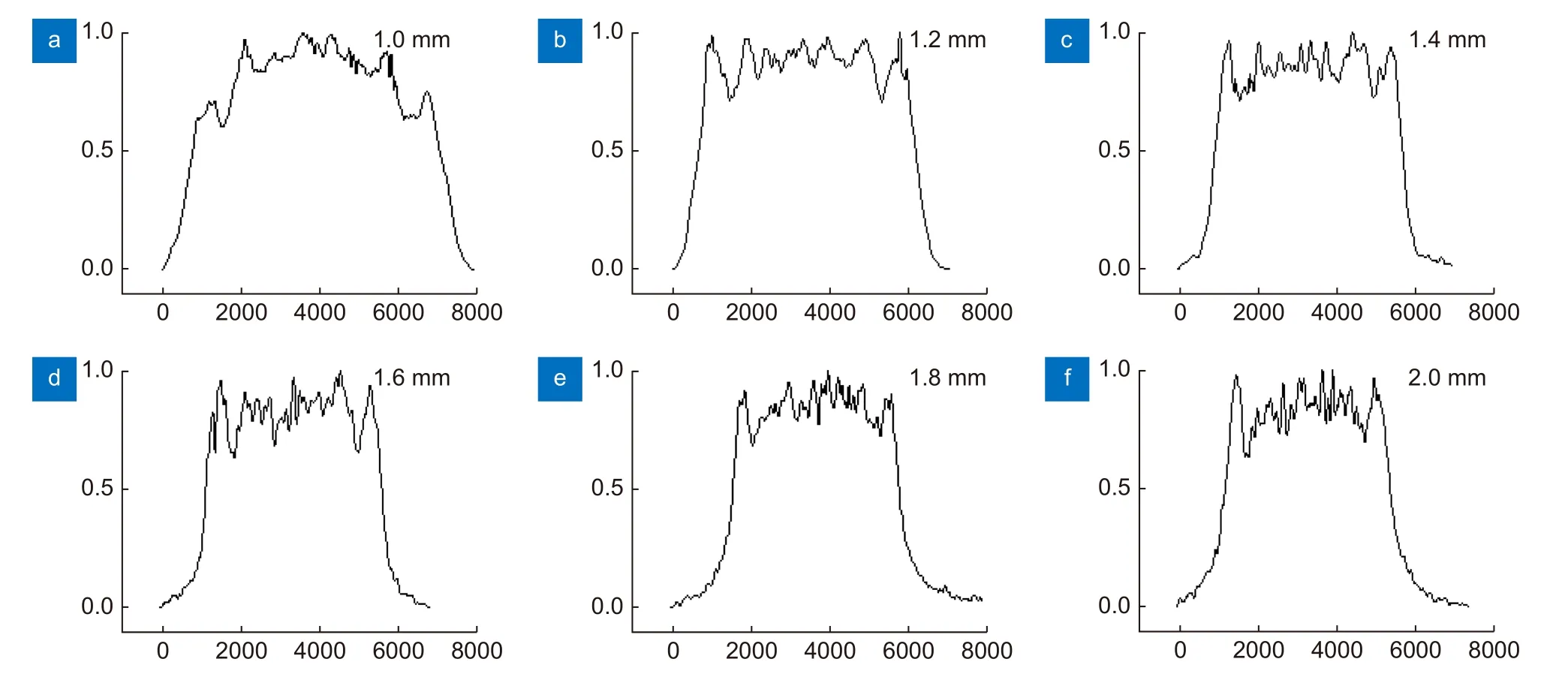
图5 不同入射光束直径对应的光强分布图。(a) D=1.0 mm；(b) D=1.2 mm；(c) D=1.4 mm；(d) D=1.6 mm；(e) D=1.8 mm；(f) D=2.0 mmFig.5 Light intensity distribution maps corresponding to different incident beam diameters.(a) D=1.0 mm;(b) D=1.2 mm;(c) D=1.4 mm;(d) D=1.6 mm;(e) D=1.8 mm;(f) D=2.0 mm

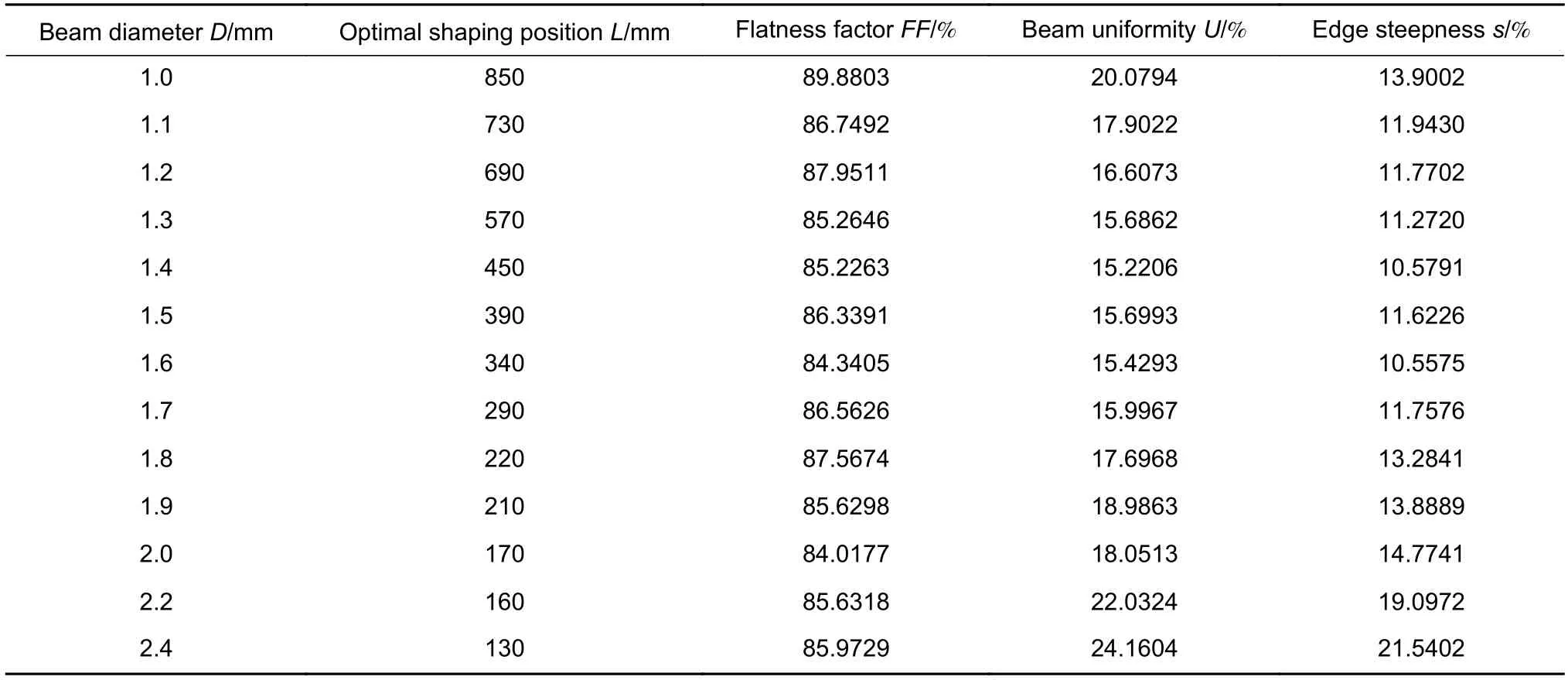
表2 入射光束直径对非球面整形的影响Table 2 Influence of incident beam diameter on aspheric shaping

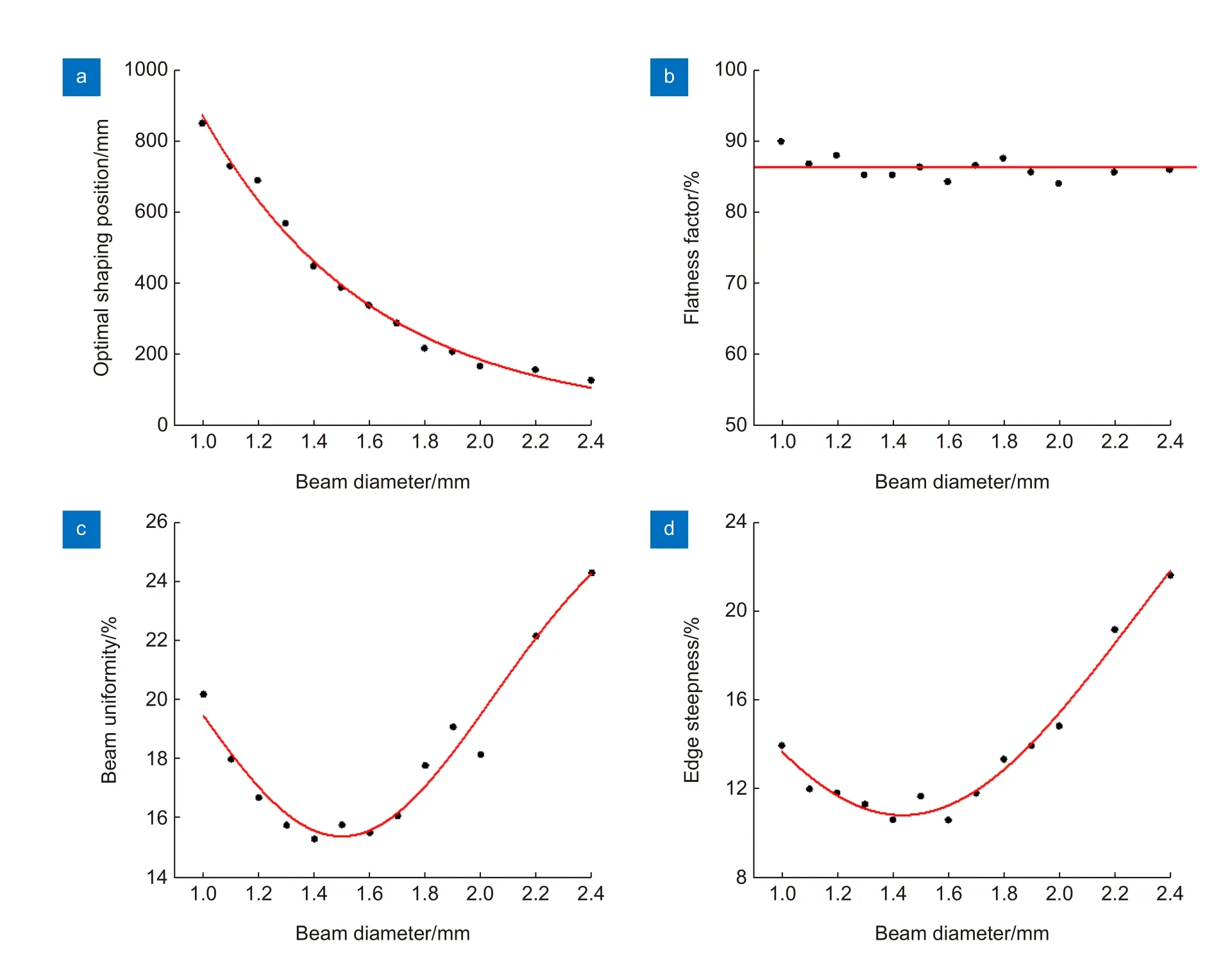
图6 入射光束直径与最佳整形位置、平坦因子、光束均匀性和边缘陡度的拟合曲线。(a) D-L 拟合曲线；(b) D-FF 拟合曲线；(c) D-U 拟合曲线；(d) D-s 拟合曲线Fig.6 Fitting curves of incident beam diameter with optimal shaping position,flatness factor,beam uniformity and edge steepness.(a) D-L fitting curve;(b) D-FF fitting curve;(c) D-U fitting curve;(d) D-s fitting curve

3.2 入射发散角对整形效果的影响

使用如图3 装置，分别使用不同焦距的透镜改变入射光束的发散角，之后将整形镜放于入射光斑直径为1.4 mm 的位置处，得到不同入射发散角对应的整形最佳位置，以及该位置处的光强分布如图7，再经过数据处理得到其平坦因子、光束均匀性和边缘陡度，见表3 。

将表3 数据进行拟合，分别得到最佳整形位置、平坦因子、光束均匀性、边缘陡度与入射光束直径之间的关系，如图8。

实验发现随着入射发散角增加，最佳整形位置越来越靠近整形镜，并且靠近速度逐渐加快；光束均匀性与边缘陡度均是先变好再变差，存在最佳入射发散角，通过计算拟合曲线最低点对应横坐标，得到光束均匀性最好的入射发散角为8.6 mrad，边缘陡度最小的入射发散角为8.1 mrad。但是研究发现入射发散角同样对平坦因子没有明显的影响，平均分布在85%左右。

4 响应曲面法探究最佳整形位置与入射光束直径和发散角的关系

4.1 实验设计

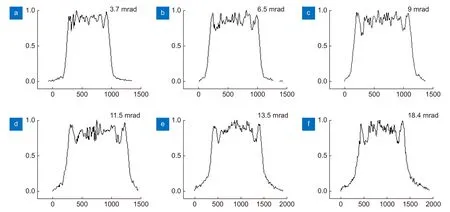
图7 不同入射发散角对应的光强分布图。(a) θ=3.7 mrad；(b) θ=6.5 mrad；(c) θ=9 mrad；(d) θ=11.5 mrad；(e) θ=13.5 mrad；(f) θ=18.4 mradFig.7 Light intensity distributions corresponding to different incident divergence angles.(a) θ=3.7 mrad;(b) θ=6.5 mrad;(c) θ=9 mrad;(d) θ=11.5 mrad;(e) θ=13.5 mrad;(f) θ=18.4 mrad

表3 入射发散角对非球面整形的影响Table 3 Influence of incident divergence angle on aspheric surface shaping

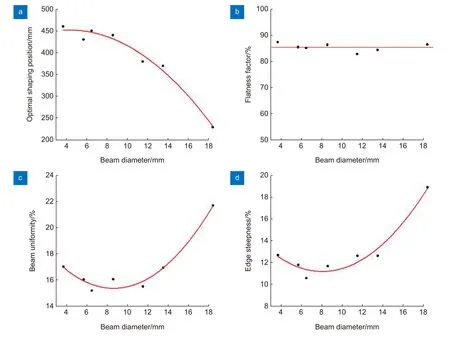
图8 入射光束发散角与最佳整形位置、平坦因子、光束均匀性和边缘陡度的拟合曲线。(a) θ-L 拟合曲线；(b) θ-FF 拟合曲线；(c) θ-U 拟合曲线；(d) θ-s 拟合曲线Fig.8 Fitting curve of incident divergence angle with optimal shaping position,flatness factor,beam uniformity and edge steepness.(a) θ-L fitting curve;(b) θ-FF fitting curve;(c) θ-U fitting curve;(d) θ-s fitting curve

为了得到最佳整形位置与入射光束直径和发散角之间的关系，本文选择响应曲面法进行探究。通过Design-Expert 软件中Central Composite 实验设计方法进行响应曲面模型的建立，其中入射光束直径与发散角作为两个自变量因素，每个因素设置5 个水平，光束直径的取值范围为1 mm～2 mm，发散角的取值范围为3.7 mrad～13.5 mrad，各因素的实验设计水平如表4 所示，用CCD 仪器寻找最佳整形位置并作为因变量，得到实验结果如表5 所示。

4.2 实验结果分析

根据表5 的实验数据，应用Design-Expert 软件得出最佳整形位置的方差分析结果如表6 所示，模型显著性检验的 P 值＜0.0001，远小于界定值 0.05，表明该模型具有统计学意义，且模型较为显著。样本R2是衡量模型拟合度的一个量，其值越接近1 说明拟合度越好，在本实验中R2值为0.98，Adj-R2为0.97，预测R2为0.94，说明实验结果和预测值比较接近。在模型有效的情况下，要求信噪比大于4，而本实验中信噪比为33.1。以上表明该模型可表示最佳整形位置与入射光束直径和发散角的关系，并且通过拟合得到预测函数式：

式中：

θ——入射光束发散角；

D——入射光束光斑大小；

L——整形镜后最佳整形位置。

随机选择多组数据对所得预测函数进行验证实验，如表7 所示。结果表明，最佳整形位置的最大预测误差为10.19%，该模型能够较好地描述响应，这表明通过响应曲面法建立的模型进行分析和预测是可行的。

表4 实验影响因素与实验设计水平Table 4 Experimental influencing factors and experimental design level

表5 实验数据表Table 5 Experimental data table

表6 最佳整形位置方差分析表Table 6 Analysis of variance of the optimal shaping position

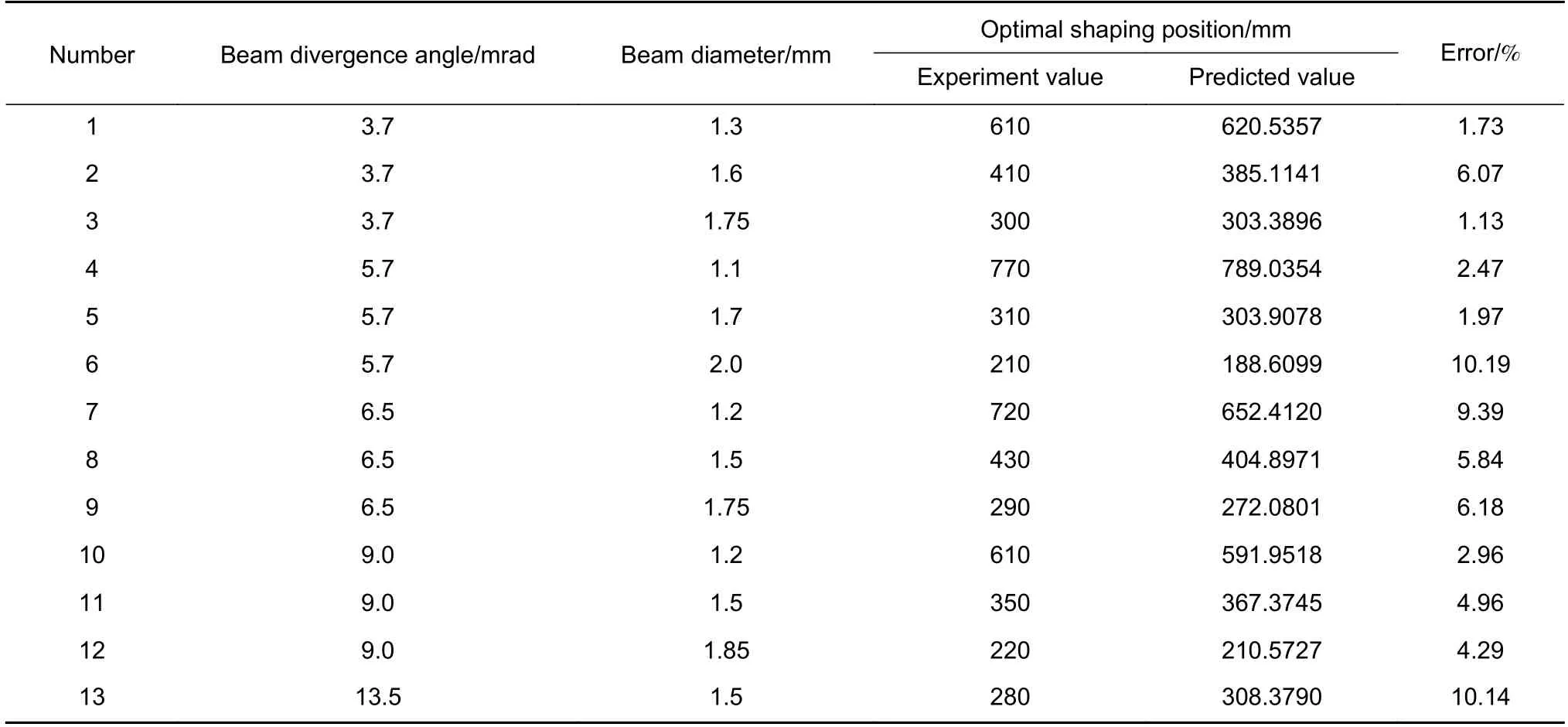
表7 预测函数验证实验Table 7 Verification experiment of predictive function

5 结 论

通过对入射光束束腰以3 mm 设计的非球面整形镜进行实验，得到以下结论：1) 不同的入射光束直径或发散角均可以通过改变传输距离得到一个最佳整形位置；2) 入射光束直径和发散角的改变对最佳整形位置上整形结果的平坦因子没有明显影响，但光束均匀性和边缘陡度会有最佳值，因此存在最佳入射参数；3) 最后利用响应曲面法得到最佳整形位置与入射光束直径和发散角的数学模型，在对不同高斯光束整形时，可以根据其入射光斑大小与发散角得到整形最优位置，使非球面整形镜的使用更加方便。