非球面透镜表面特性理论分析

许金凯，丁戗，于化东，王志超

（长春理工大学 制导与对抗技术研究所，长春 130022）

非球面透镜作为一个重要的光学元件，在光系统中占有着重要的地位［1-3］。一个非球面透镜在光系统中起到的作用要优于3-4个球面透镜［4］，主要是因为球面透镜在光系统中存在球差，比如横向偏差、轴向偏差和角度偏差，从而限制了球面透镜在光学系统中的应用。而非球面透镜具有消除球差的能力，从而大大的提高了非球面透镜在光系统中的使用范围。

对非球面透镜的研究主要在两个方面。1.采用光学设计软件（比如CODE V和ZEMAX）对非球面透镜进行设计，从而解决非球面透镜中的光线传输和成像问题［5］；2.采用针对非球面的制备过程进行研究［6］。

国外在非球面表面拟合度方面进行了比较深入的研究，对非球面拟合方法研究较少。Héctor提出了一个适合于圆锥非球面曲线算法［7］；ZHANG基于线性最小二乘法提出了非球面参数计算算法［8］；Gugsa等通过改变圆锥常数k的值，利用最小二乘法的最值法来得到标准表面的最佳轮廓［9］。以上方法只考虑单一标准曲面表面，且在测量非球面时，圆锥常数k的估算会因为多项式系数的不同而产生偏差［10］。

在本文中，通过理论分析，建立了非球面表面特性函数，并且以K9玻璃为例，讨论了非球面表面特性函数，并对其拟合误差进行分析。

1 理论分析

图1为非球面透镜的分析示意图，光线通过一个非球面透镜两次折射后，聚焦到O点。其中Q点和P点分别为非球面透镜的曲面和平面上的两点，即光线折射的两点。假设非球面透镜的折射率为n1，透镜的左边和右边的介质折射率分别为n0和n2。光线的入射角为φ，经过第一次和第二次折射后，折射角分别为 δ和θ。根据Snell定律，我们可以得到在P点和Q点的折射方程分别为：

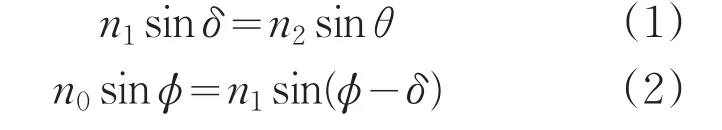
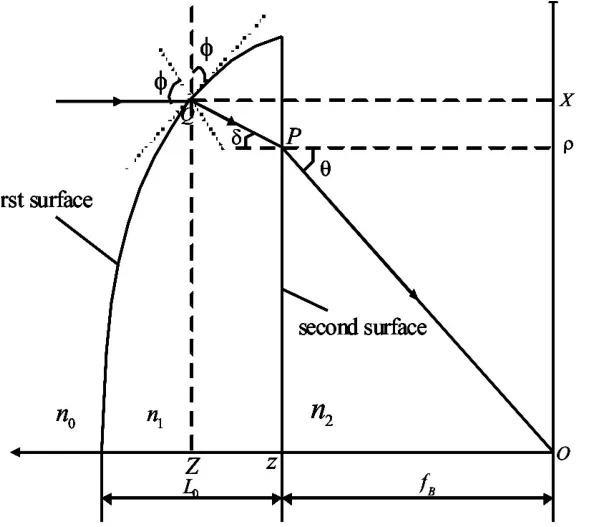
图1 非球面透镜表面特性计算示意图Fig.1 Schematic diagram of surface profile calculation of a aspherical lens

在柱坐标系下，Q点和P点的坐标可以表示为Q(X,Z)和P(ρ,z)，由于非球面透镜的第二个表面为平面，因此，P点坐标可以表示成如下函数形式：

在非球面透镜的第一面上的Q点，其坐标也可以表示成如下函数形式：

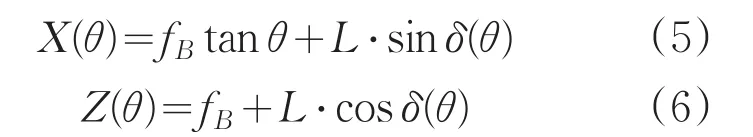
其中 fB为非球面透镜的后焦距，L为非球面表面特性函数。

通过对方程（5）和（6）进行求导，我们可以得到以下方程：

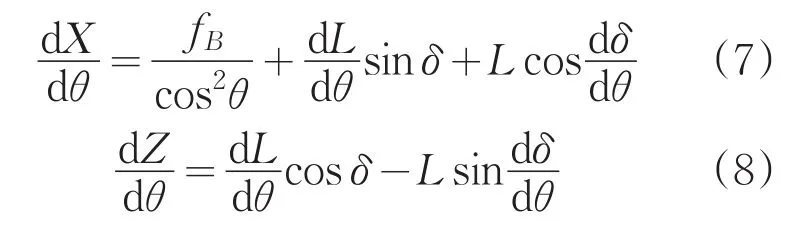
利用三角函数关系，我们有

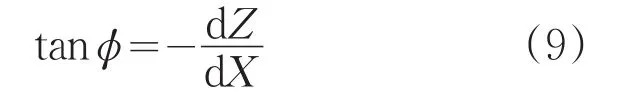
由于Z和X是θ的函数，因此方程（9）可改写为：

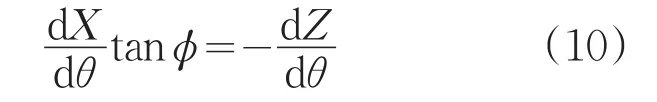
将方程7和8代入到方程（10）中，并且令

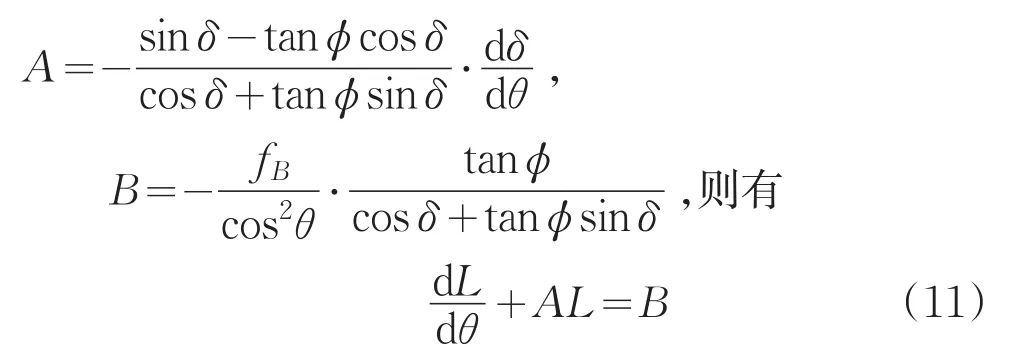
其中A，L和B都是θ的函数。

在方程（11）两边乘以未知函数F（F为θ的函数），

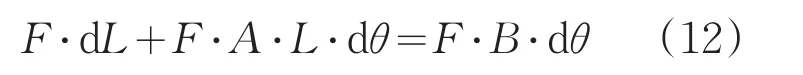
通过对方程（12）的左边进行积分，并经过位置变换后，可以得到

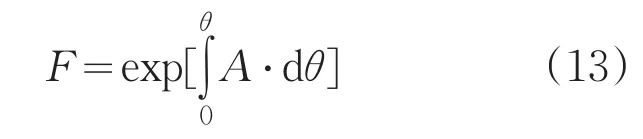
将方程（13）代入带方程（12）中，则有

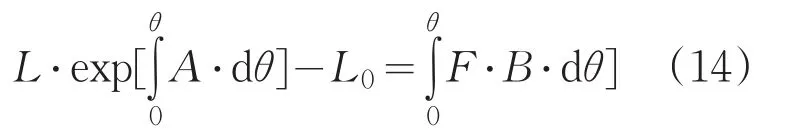
因此我们可以非球面表面特性函数

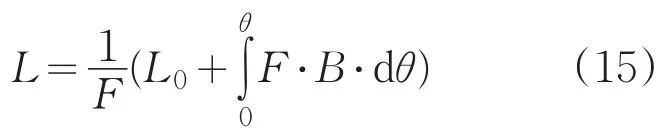
将方程（1）两边同时对θ求导得

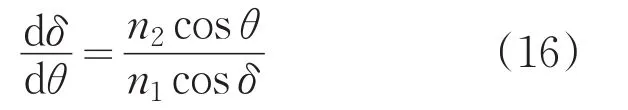
将方程（2）和（16）代入到函数A、B中，则有：

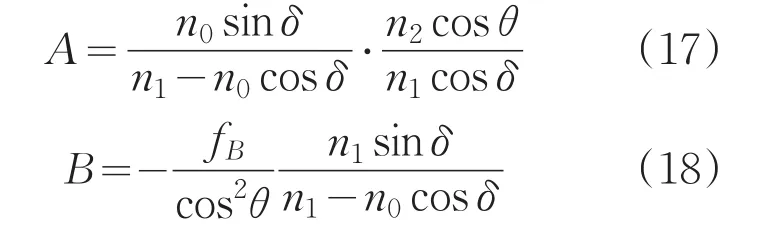
在方程（1）中，我们将δ表示成为θ的函数：

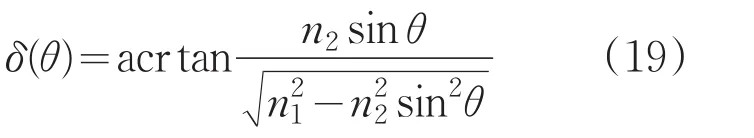
因此函数A和B可以进一步表示为

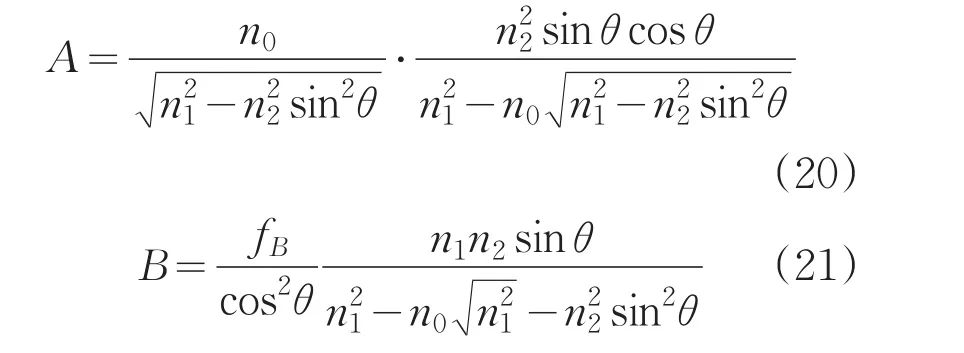
将方程（13）、（17）和（18）代入到方程（15）中，我们最终可以完全得到非球面表面特性函数。

2 结果与讨论

我们以K9玻璃为例，折射率为n1=1.5163，并且假设非球面透镜两边的介质都为空气，折射率为n0=n2=1，非球面透镜的厚度和后焦距都为50mm，最大折射角为θ=450。经过分析后，绘制出如图2所示的非球面透镜的表面特性曲线。

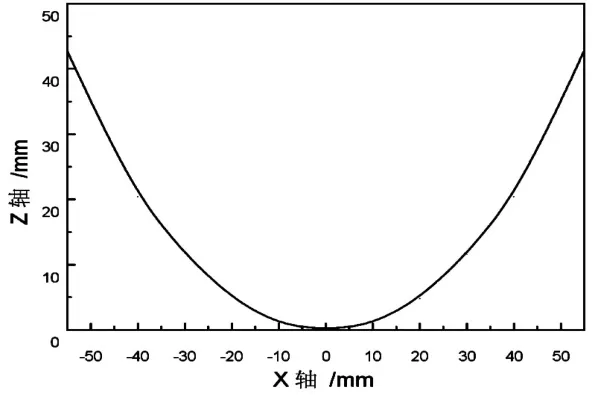
图2 非球面透镜表面透镜计算图Fig.2 Calculating diagram of surface profile calculation of an aspherical lens

式中，R是曲率半径，k是二次曲面常数，Ci是非球面形变常数。设置了如表1所示的参数。图3为非球面透镜的拟合误差曲线，从曲线中我们可以看出非球面透镜表面特性的拟合误差小于±30nm。

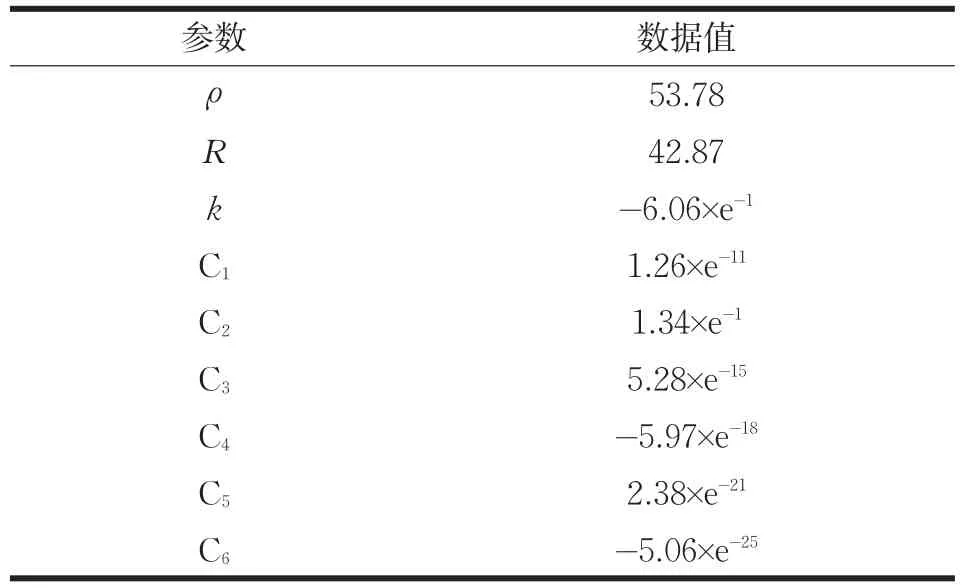
表1 非球面透镜表面特性公式拟合数据Tab.1 Fitting dates of the surface profile to a aspheric lens formula

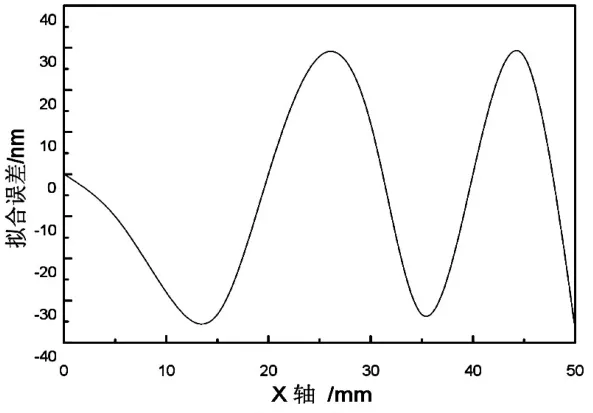
图3 非球面透镜表面特性公式拟合误差Fig.3 Fitting error of the aspherical surface profile formula

3 结论

本文通过对非球面透镜的进行设计的基础上，建立了非球面透镜表面特性函数。以K9玻璃为例，绘制出了非球面透镜的表面特性曲线。通过对非球面透镜的表面特性曲线进行分析，认为其拟合误差小于±30nm，表明了该非球面透镜的特性函数方程具有较高的精确性，在对非球面透镜的设计和制备过程中具有重要的参考价值。

［1］张忠玉，张学军，牛海燕.中小口径非球面元件加工技术的探讨［J］.光学技术，2001：27（6）：524-525.

［2］Yeon Hwang，T.Kuriyagawa，Sun-Kyu Lee.Wheel curve generation of aspheric microgrinding in parallel grinding method［J］.International Journal of Machine Tools&Manufacture，2006（46）：1929-1933.

［3］Taik-Min Lee，Eung-ki Lee，Min-yang Yang.Precise bi-arc curve fitting algorithm for machining an asphericsurface［J］.IntAdvManufTechnol，2007（31）：1191-1197.

［4］J S Chahl，M V Srinivasan.Reflective surfaces for panoramicimaging［J］.Applied Optics，1997，36：8275-8285.

［5］熊德平，何志平.非球面光学系统的光路计算与分析［J］.光学仪器，2004，26（4）：45-47.

［6］潘君骅.非球面光学系统设计、加工及检验的综合考虑［J］. 光学技术，2001，27（6）：566-567.

［7］Aceves-Campos H.Profile identification of aspheric lenses Applied Optics［J］.Applied Optics，1998，37（34）：8149-8150.

［8］Zhang Z.Parameter estimation techniques：a tutorial with application to conic fitting［J］.Image and Vision Computing，1997，15（1）：59-76.

［9］Gugsa S，Davies A.Monte Carlo analysis for the determination of the conic constant of an aspheric micro lens based on a scanning white light interferometric measurement［C］.In：Hatheway Alson E.editors：Proceedings of the SPIE，2005，92-102.

［10］Sun W，McBride J W，Hill M.A new approach to characterising aspheric surfaces［J］.Precision Engineering，2010，34（1）：171-179.