基于模糊聚类与机器学习的医疗数据统计分析算法设计

王晨宇，陈曦，林昊，潘利民，徐国刚

（河北北方学院附属第一医院，河北张家口 075000）

近年来，医药卫生体制改革正在我国逐步推行，以加强卫生经济管理和促进医疗费用的降级[1-2]。“看病难”、“看病贵”已成为影响人们生活的社会问题，如何降低医疗费用、合理利用医院资源成为了当前相关学者的重点课题之一[3-5]。

为了研究医疗费用和医疗资源使用情况之间的关系以及影响医疗费用的因素，目前已有多名学者发表了针对单病种的研究成果[6-10]。单病种通常指不存在并发症的疾病，对其医疗费进行规范化管理是现阶段我国医保部门控制费用的方法之一。患者在享受医疗服务后，根据疾病的种类和相关检查、手术，按照一定的比例进行付费。单病种付费在一定程度上降低了人均医疗费用，但在住院时间管理、单病种种类等方面仍存在不足[11-16]。

为进一步综合分析影响医疗费用的因素及医疗费用构成是否合理，文中使用模糊聚类对患者治疗过程中的相关信息进行特征提取与因素分析，并采用机器学习中的BP 神经网络构建了医疗费用数据分析模型。

1 单病种医疗数据统计分析

单病种医疗数据统计分析主要为医疗费用的分析，充分考虑不同种类单病种的特点，同时多角度分析该种医疗费用的影响因素，实现诊断、治疗成本的控制，进而降低患者的医疗费用并控制医疗资源的浪费。

现阶段的医院门诊与患者所有单据主要有4类：就诊记录表、手术信息表、诊断记录表和收费明细表。根据这些表格和近年来的文献，整理出如表1所示的影响医疗费用的因素。在所整理的数据结构与内容的基础上，建立了基于患者、诊断、手术、医院四者关系的医疗费用分析框架，具体如图1 所示。

表1 医疗费用影响因素

图1 医疗费用分析框架

医院和患者所有的单据上主要有数字和文字两种信息，由于数字与文字结构的不同，因此需要进行数据预处理以便进行多源异构数据的融合。数据预处理包含数据清洗、特征提取、特征融合。数据清洗主要针对重复信息、数据缺失、异常数据这3 种情况，将无效数据去除。其中重复信息采用字段匹配的方式来识别，通过对各字段分词、排序，分组检测前后分词的相似性。数据缺失分为两种情况：一类是关键词缺失，例如患者姓名、身份证信息、医保账户等能够关联各个单据的关键词信息缺失；另一类是非关键词缺失，主要指患者身份信息、诊断内容、费用明细表缺失。异常数据则主要是指数据输入错误、医疗设备数据采集异常等。

2 数据分析算法设计

2.1 影响因素分析

文中使用模糊聚类来分析影响医疗费用的因素比重。在未明确各因素的影响时，引入隶属度来表征各因素与医疗费用之间的关系，具体如下式所示：

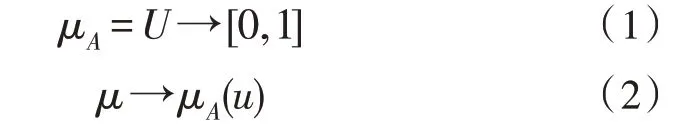
式中，集合A为论域U的一个模糊子集，元素u属于集合A的概率被定义为元素u到集合A的隶属度，使用μA表示。此处，μA为论域U到[0,1]的一种映射关系。因此，集合A可用下式来描述：

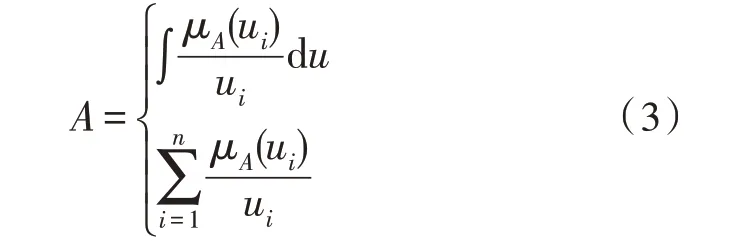
根据研究问题的特性，论域U可分为连续和离散两种情况。当论域U为连续集合时，使用式（3）中的积分表达式计算；当论域U为离散集合时，使用式（3）中的求和表达式计算。模糊集合内的元素具有相应的计算规则，该规则使用五元组来表示，即(x,T(x),X,G,M)。在五元组中，x为变量，T(x)为定义在论域X上的模糊集合，G为产生语言变量x值名称的语法规则，M为产生模糊集合的隶属度函数。

由于模糊理论在进行数据处理时，不能进行自适应学习。而医疗数据，尤其是患者医疗费用数据涵盖了多种信息，直接使用模糊聚类则需要重复运算。因此，文中引入机器学习中的BP 神经网络来提高自适应学习能力。

2.2 基于改进BP神经网络的数据分析

BP 神经网络通常由输入层、隐藏层和输出层构成，根据每次训练的结果与预想结果的偏差来修改层与层之间的网络权值及阈值，进而提高训练结果和预想结果的一致性。BP 神经网络的基本结构为神经元，如图2 所示。

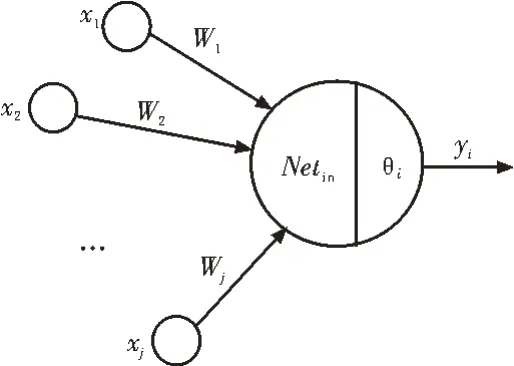
图2 神经元结构模型示意图

神经元给每个输入分配不同的比例，再以某种方式进行融合，融合结果Netin与阈值θi比较之后，经过激活函数处理后传递下一个神经元。使用w1，w2,…,wj来表示各个输入的比例，融合方式采用线性加权求和方式以降低计算量，如式（4）所示：

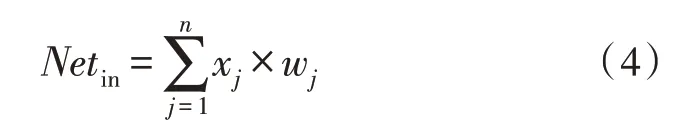
Sigmod 函数被用来作为神经元激活函数，其函数的输入范围大，包含负无穷大到正无穷大，输出范围为[0,1]。因此，该神经元最终输出可用下式来表示：

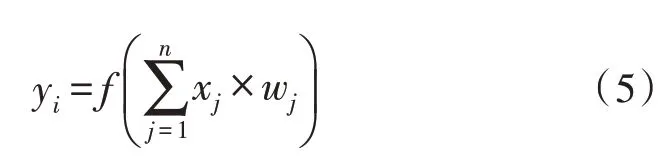
用于单病种医疗费用数据分析的BP 神经网络模型结构如图3 所示。由于影响医疗费用的因素过多且单个样本数据量较少，为提高BP 神经网络模型的学习效率，在隐藏层与输出层之间增加分类器。对于输出层与隐藏层之间神经元的权重，使用vih来表示；隐藏层第h层各神经元的权重使用θh来表示；隐藏层与隐藏层、隐藏层与分类器、分类器与分类器之间的神经元权重使用whp来表示；隐藏层到输出层神经元之间的权重用wpj来表示；输出层神经元的阈值使用θj来表示。隐藏层的层数与神经元的个数影响着训练的效率和时间。

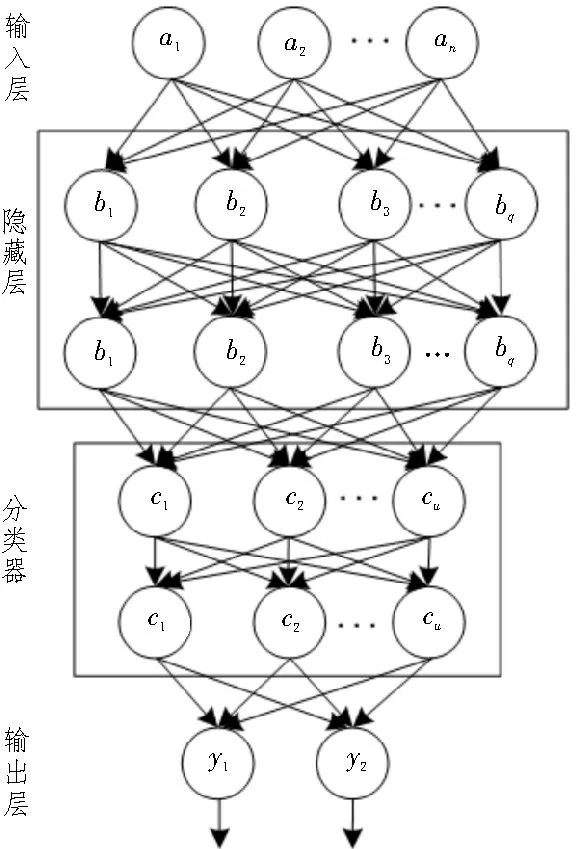
图3 医疗费用数据分析模型结构

在进行BP 神经网络模型训练时，需要对各个权重赋予初始值，其值为区间（-1，1）之间的随机数，并约定误差函数e、计算精度E和最大学习次数M。在样本数据中随机选择训练样本进行模型训练，则第k个样本和期望输出可表示为：

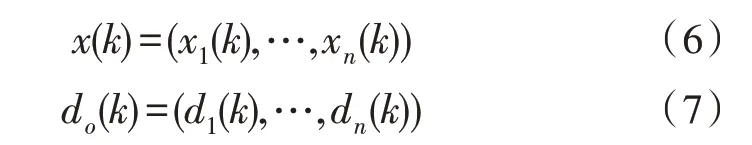
隐藏层各个神经元的数值与输出给下一层神经元的数值可表示为：

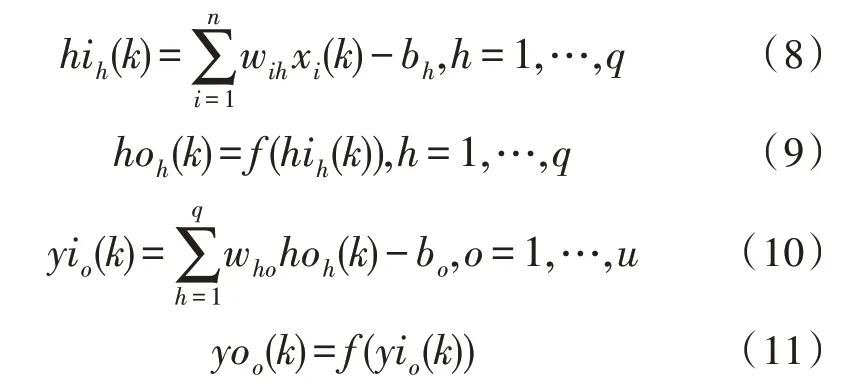
在得到隐藏层、输出层神经元数值后，利用最小二乘法得到与期望数值的误差，可表示为：

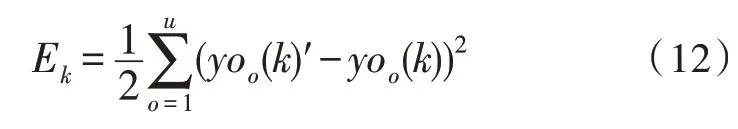
利用误差来修正各个权值，由于函数沿着梯度的方向变化速度最快，因此使用梯度下降法来更新BP 神经网络参数，具体如下式所示：

式中，η为学习速率，该值过大则容易错过最优解；反之，BP 神经网络模型训练速度过慢，则影响效率。在修正各层神经元的连接权重后，计算全局误差e。当全局误差e小于预设计算精度E或训练学习次数大于设定的学习次数M时，则终止算法；否则，选取下一个样本数据进行训练。全局误差e的计算方式为：

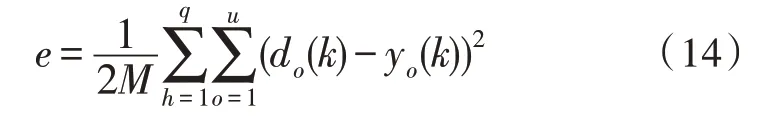
3 数据测试与验证

模糊聚类和BP 神经网络模型的使用需要大量的数据支撑。为获取足够的训练和测试样本数据，调取了某医院2020 年度住院患者的基本信息和相关单据，并对数据进行预处理。训练与测试样本数据共包含40 万位患者的诊断、治疗信息，数据量达1 120 万条。测试仿真采用Matlab 7.0 仿真平台，计算机配置为具有16.0 GB 内存、500 GB 固态硬盘、2.4 GHz Inter(R)至强可扩展处理器。

图4 展示了不同隐藏层层数与神经元个数对BP神经网络模型聚类精度的影响。从图中可以看出，隐藏层层数和神经元个数的增加对聚类精准度的提高均具有改善作用。值得注意的是，隐藏层层数的增加会显著提高聚类精准度收敛的速度及收敛值。当神经元个数为35、隐藏层层数为2、3、4、5 时，聚类精度均达到收敛状态。而在图5 中可以看到，神经元个数的增加可降低训练时间，且隐藏层层数的增加会增大整体的训练时间。这主要是由于BP 神经网络在进行模型权重修正时采用逆向传递，隐藏层层数的增加会增大计算量。因此综合聚类精度与训练时间两个方面，医疗费用数据分析模型采用4 层隐藏层，每层35 个神经元的配置。

图4 不同隐藏层数下神经元个数与聚类精准度的关系

图5 隐藏层层数和神经元个数对训练时间的影响

基于模糊聚类和机器学习的医疗费用数据分析算法与基于Adaboost 算法的数据分析对比，如表2 所示。其中，两种算法均采用相同的训练和测试数据。与文中采用双层分类器不同的是，Adaboost 算法仅有一层分类器层，各个分类器的权重影响着分类精度。在表中，文中所述方案的分类精准度在两种样本数据测试下，平均精准度比Adaboost 算法高5.75%，这是由于双层分类器的设置提高了分类器的识别能力。

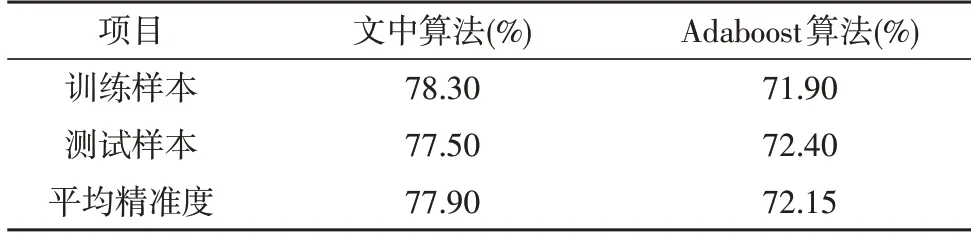
表2 两种算法的数据分析精准度对比

4 结束语

文中通过分析单病种患者的个人信息与病情、诊断、收费项目等内容，使用模糊聚类来对相关信息进行特征提取及分析影响医疗费用的因素，并采用机器学习中的BP 神经网络构建了医疗费用数据分析算法。该算法为综合分析影响医疗费用的因素与医疗费用构成是否合理提供了新的途径。