区间值Riemann-Liouville型分数阶积分等式

刘 靖，史芳芳，叶国菊，刘 尉

(河海大学 理学院，江苏 南京 210098)

0 引 言

随着电子计算机技术的迅速发展，科学技术和工程中的许多问题对计算的需求也越来越高，误差问题在数值运算中日益凸显.不仅有来源数据的误差，还有计算过程中截断误差的积累等.如何保证计算结果的精度和可靠性，成为计算数学面临的迫切需要解决的问题.1966年，Moore[1]将区间方法应用到数值计算中的自动误差分析，提高了计算结果的可靠性，进一步讨论了区间值函数的积分理论.此后，区间分析作为处理不确定性问题的一种新的有效工具被广泛应用于自动误差分析[2]、计算机图形学[3]、神经网络输出优化[4]等领域.区间值函数作为一种特殊的映射，其函数凸性、连续性、可积性等基本性质已经得到了充分完善.但是，对于2个任意的区间[A]和[B]，若[A]+[B]=0，得不到[A]=-[B].这意味着区间减法和导数不满足一般情况.为了完善区间分析理论，Hukuhara在文献[5]中给出了Hukuhara差(H-差)的定义;但是，当区间[A]的长度小于[B]的长度时，[A]⊖[B]就不存在了.Stefanini[6]建立了广义Hukuhara差(gH-差)和广义Hukuhara导数(gH-导数)的定义.由于广义Hukuhara差是始终存在的，因此受到了众多学者的广泛关注.

另一方面，与积分有关的不等式在数学的基础理论和应用研究中一直起着非常重要的作用.2013年以来，一些经典的积分不等式被推广到区间值函数的形式中,如区间值函数的 Hermite-Hadamard不等式[7-8]、Ostrowski不等式[9]和Jensen不等式[8,10]等.此外，Lupulescu在文献[11]中给出了区间值Riemann-Liouville分数阶积分的定义并证明了相关的重要性质.随后，Büdak等[12]将积分不等式与区间分数阶积分相结合，得到了一类新的Hermite-Hadamard型不等式.gH-可导的区间值函数是否可以与区间分数阶积分相结合呢？答案是肯定的.本文中，笔者的主要研究内容是构造区间映射，利用区间值函数的性质和分数阶积分理论对实值函数的积分等式进一步加细，建立一类新的区间值Riemann-Liouville型分数阶积分等式，并给出了相应的例子来证明所得结果的准确性.另外，该结果可以成为研究gH-可导区间值函数积分不等式、区间微分方程、区间优化等内容的有利工具.

1 预备知识

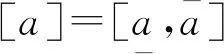
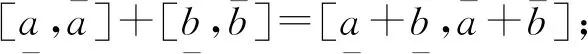
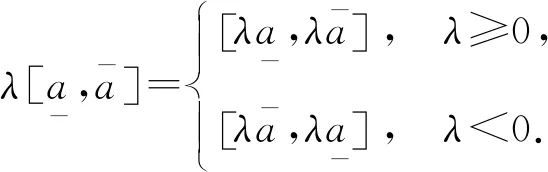
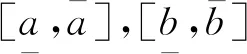
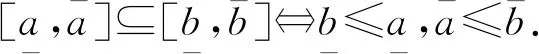
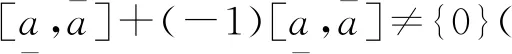
但是，任意2个区间并不一定存在H-差.为了避免这种情况，Stefanini[6]引入了gH-差:

定义1[13]设f:[a,b]→Rx.如果存在f′(t0)∈Rx使得

那么称f在t0处是gH-可导的.若∀t0∈[a,b]，f′(t0)∈Rx都存在，则称f在区间[a,b]上是gH-可导的.

定义2[13]如果实值函数t→w(f(t))在区间[a,b]上是单调增加(单调减少)的，那么称f:[a,b]→Rx在区间[a,b]上是w-单调增加(w-单调减少)的.若f是w-单调增加或w-单调减少，那么称f在区间[a,b]上是w-单调的.

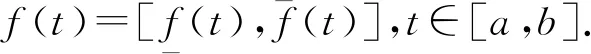
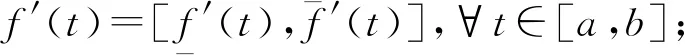
一般来说，同课异构有两种形式：一是同一个文本由不同的执教者进行施教，组织课堂教学，即多人同课异构；二是同一个文本由同一个执教者进行施教，在不同的教学班级，通过不同的构思和处理组织课堂教学，即一人同课异构。

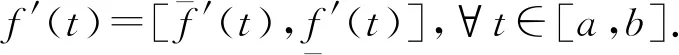
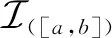
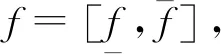
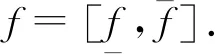
其中α>0,Γ是Gamma函数.

2 主要结果

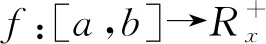
证假设f是w-单调增加的，有

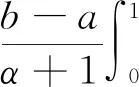
类似地，若f是w-单调减少的，可以得到同样的结论.

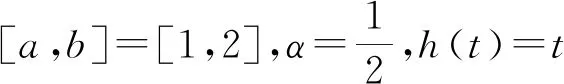
那么对任意的x∈[1,2]，有

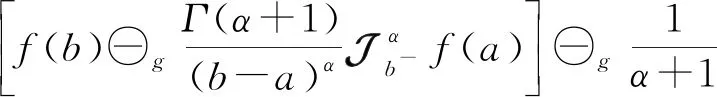
且

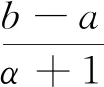
因此，定理1成立.

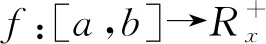
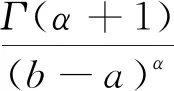
证假设f是w-单调增加的，有

类似地，若f是w-单调减少的，可以得到同样的结论.

例2如例1所设，有

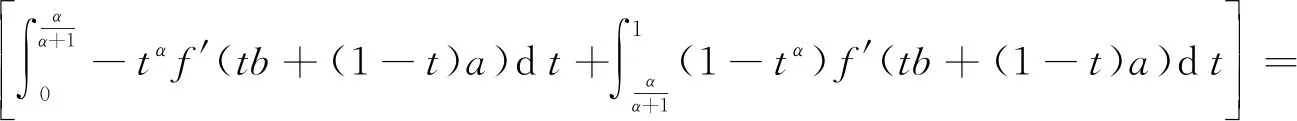
因此，定理2成立.