一种精确图像待配准区域的快速配准算法*

国艺美 毕 波 唐锦萍 辛德元

（1.东北石油大学数学与统计学院 大庆 163318）（2.海南医学院公共卫生与全健康国际学院 海口 571199）（3.黑龙江大学数据科学与技术学院 哈尔滨 150080）

1 引言

在计算机视觉［1］中，图像配准是其非常重要的研究领域，而图像配准更是图像处理研究中一个不可避免的典型问题。近年来在图像配准方面提出了多种图像配准方法［3］。经研究表明，人们越来越重视基于特征的图像匹配方法，其在移动机器人导航［7］、运动识别［8］、三维立体重建［9］等方面都得到了大范围的应用。David Lowe等在1999年提出了SIFT（Scale Invariant Feature Transformation）算法［10］，该算法对多种图像变化和外界条件变化对图像配准的影响具有鲁棒性，因此在图像配准领域应用广泛。由于SIFT算法的最大缺点是描述子的构建时间过长，不具有实时性，从而引发了大家纷纷研究的热潮。在众多的研究算法中，大多数改进算法是针对减少算法运行所花费时间的问题［11］。例如2008年，刘立等［13］采用基于圆形框的12维向量有效表示一个特征点的方法，以此降低了时间复杂度。2010年，刘健等［14］采用了对数极坐标变换进行图像粗匹配，结合欧氏距离和Procrustes迭代算法［15］获得图像的相应特征点对，最终完成图像配准的方法。

本文受在2017年张红民等［16］提出算法的启发，算法采用对待匹配图像分块，根据各子块信息熵［17］大小决定是否进行特征提取的算法。由于其算法是将子图特征类型判断阈值设置为经验值，没有根据子图的信息自适应来设定阈值，现针对此问题做出改进，并新增剔除二值化图像［18］连通区域［19］的方法，进一步精确图像中需要提取特征的待检测区域。

2 SIFT算法匹配步骤

2.1 尺度空间极值的检测

首先建立高斯尺度空间和DOG金字塔，每个点若是其DOG空间上下两层即26个邻域内的极值，则该点为特征点。再通过曲线拟合，低对比度筛选和消除边缘效应确定最终的特征点。

2.2 确定特征点主方向

以每一特征点的邻域梯度方向上的分布特征作为该点的主方向，以此来保证特征点具有旋转不变性

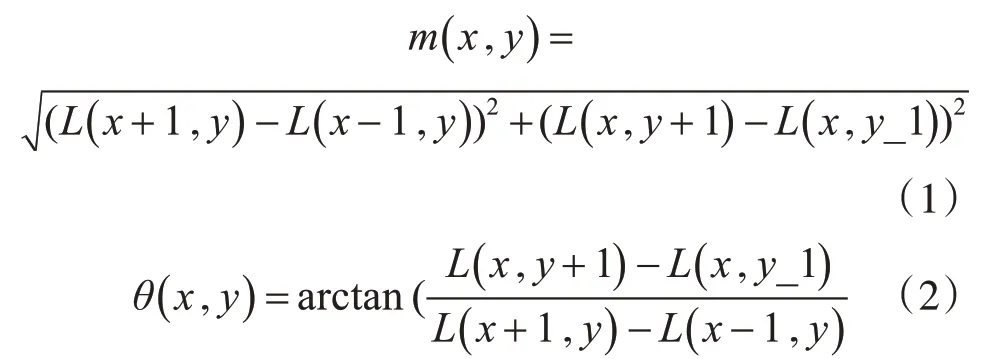
式（1）、（2）分别为（x，y）处的模值和方向公式，L即该特征点所对应的尺度。在这里需加上一个权重，也就是以特征点为圆心做高斯滤波，给它周围的点加上一个高斯权重。高斯函数的方差是与这个特征点所在图像层的尺度σ有关的，也就是1.5σ。然后在以关键点为中心的邻域内采样，用直方图对其像素分布进行统计。其中直方图范围为0～360°，每10°作为一个单位，一共有36个方向。该点邻域梯度的主方向就是直方图的最大值的方向，辅助方向则是大于最大峰值80%的方向。

2.3 特征点描述子

在以特征点为中心的16×16的窗口内，再将其均匀分成4×4的小窗口，然后计算每个子窗口8个方向的梯度累计值，从而生成了4×4×8=128维的特征向量。

3 一种精确图像待匹配区域的快速配准算法

SIFT算法的众多优良特性使其具有很好的研究价值，但又因为其128维特征描述子的构建花费时间较长，而使该算法不具有实时性，影响其在实际中的应用。现针对此问题，本文在张红民等的算法基础上又做了进一步的改进，旨在精确图像中待检测的区域。

3.1 待检测区域第一步筛选：图像分块

我们知道在一幅图像中，在灰度变化明显的地方必然会出现较多的特征点。所以在做图像配准时，对一张图像的检测，可以去掉没必要检测的灰度变化不明显的区域，以此来减少特征点检测和接下来描述子构建所需要花费的时间。这样做在一定程度上也避免了部分虚拟特征点的产生。

在这里，我们采用对图像循环分块，去掉子块信息熵［1］满足规定条件的子块的方法精确图像的待检测区域。具体流程如下：

1）对图像进行均匀分块，分成m×m个子块，m初始值为3（当图像的宽和高不能被整除时，对边缘像素重复计算，以此来简化算法）。计算所有子块的信息熵和所有子块信息熵的标准差。

2）对当标准差大于等于阈值T时停止分块，在这里阈值取经验值0.6。然后计算此时所有子块信息熵的均值。受切比雪夫不等式（式（3））性质的启发，其中μ为数学期望，σ2为方差，ε为任意整数，当ε=2σ时在所有数据中，至少有3/4的数据位于平均数两个标准差范围内。那么在这里为避免去除图像过多有用信息，规定在图像中仅去除所有子块中子块信息熵低于平均值减去一个标准差的部分。当阈值没达到T时，继续分块，m=m+1。m最大取10，当m为10时，标准差仍不满足条件也停止分块，以当前标准差进行正常计算。

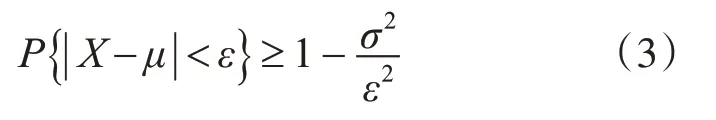
3.2 待检测区域第二步筛选：剔除连通区域

将图片二值化，求取图像连通区域，在第一步筛选后的图像待检测区域中再去除联通区域的部分，从而得到最终的待检测像素区域。

3.3 SIFT特征检测与描述，完成配准

在经过两步筛选后，对已精确待检测区域的图像进行SIFT算法特征检测并生成PCA-SIFT描述子，使用最近邻与次近邻之比的算法完成图像配准。

4 实验与结果分析

为了验证本文算法的效果进行如下实验，本实验对象为图1的三组图像。图像大小分别为：图1（a）359×403；图1（b）400×320；图1（c）400×266。

图1 三组待检测图像

首先分别计算每一组图像需要分块的数量，在这里我们的标准差（var）阈值取经验值0.6。从m=3开始将图片均匀分成m×m块，当图像的宽和高不能被整除时，对边缘像素重复计算，以此来简化算法。当标准差大于等于0.6时停止分块，计算所有子块信息熵的均值（mean），然后在整幅图像中去掉所有子块中信息熵满足式（4）的子块（在这里信息熵用ENIN表示）。每组图像经计算后，最终分块个数、信息熵标准差、信息熵均值以及去掉的子块个数如表1所示（表中数据Var、Mean、ENIN均取小数点后三位数，为近似值）。

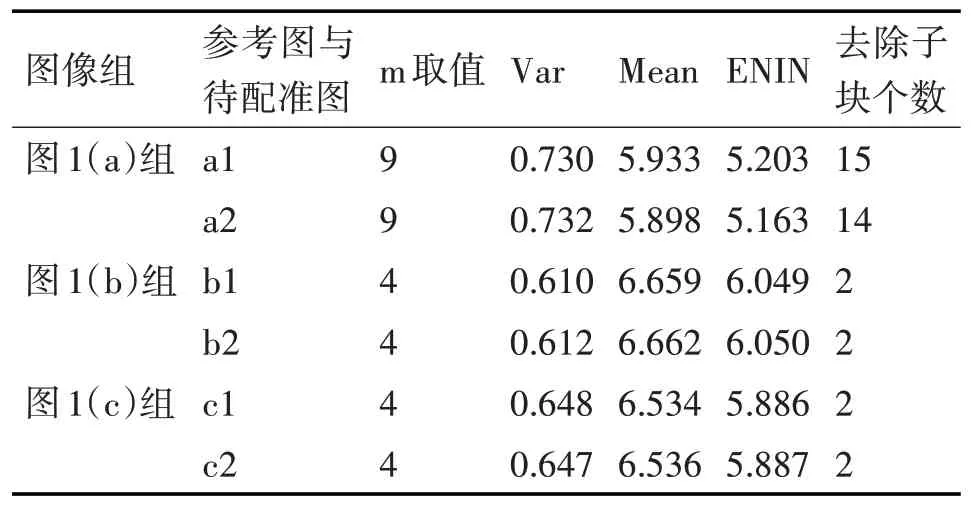
表1 三组图像实验分块结果

在这里以图1（b）组图像为例，完成去掉相应子块区域和剔除图像的二值化图像联通区域步骤，得到最终待检测区域效果图如图2所示。最终图像待检测区域为去掉有圆圈的子块部分和二值化图像白色（像素值为255）部分。

图2 图1（b）组图像需去掉子块和需剔除连通区域图展示图

三组图像最终的匹配效果图如图3所示。

图3 三组图像配准效果图

从图3中我们可以看出每组图像中特征点的数量有限且分布较为均匀，聚簇现象较少，各对特征点的匹配连线清晰可见，但也不乏有明显的匹配错误的点对。总体匹配效果良好。

为了验证本文算法在保证图像配准正确率保持在90%以上的情况下可以有效减少算法运行的时间，将其与SIFT算法和张红民等人的算法做效果做比较。分别进行三种算法的特征点数量、粗匹配点对数、正确匹配点对数、匹配正确率以及运行时间的对比，具体数据如表2所示。

表2 两种算法实验结果对比

由表2中数据可知，本文算法与其他两种算法相比明显减少了所提取特征点的数量，且匹配正确率稍有提升。由于检测出的特征点总体数量的减少，减少了构建描述符和特征点匹配所花费的时间。本文算法相比张红民等人算法运行时间减少了9%～13%，相比SIFT算法运行时间减少了20%～30%。

5 结语

本文在已有算法基础上，针对其对图像分块数的确定和通过经验信息熵阈值来确定待检测图像区域的方法做出改进。本文算法对图像进行循环分块，当所有子块信息熵的标准值达到阈值时停止分块，在整幅图像中去掉信息熵值低于信息熵均值减去信息熵标准差的子块对应的图像区域。再将图像二值化求取连通区域，在已去掉部分子块图像区域的基础上去图像的掉联通区域部分从而得到最终待检测图像区域。最后进行SIFT算法的特征检测并生成PCA-SIFT描述子，使用最近邻与次近邻之比的算法完成图像配准。

为了验证本文算法的有效性，对三组图片进行实验，实验表明本文算法在保证匹配精确度90%以上的基础上，相比张红民等人算法运行时间减少了9%～13%，相比SIFT算法运行时间减少了20%～30%。由此可证明本算法有效减少了图像配准算法的运行时间。