基于Halcon标定靶的双目相机高精度标定方法*

黄 建 李施阳 章秀华 吴锦梦

（武汉工程大学电气信息学院 武汉 430205）

1 引言

近些年，随着计算机算力的提升，三维重建技术得到广泛应用。双目立体视觉作为三维重建技术的一个重要分支，具有经济、高效的优点。相机标定是双目立体视觉技术中最基础和最重要的工作，其精度直接决定双目三维重建的效果。因此，研究一种适用于复杂应用场景的灵活、稳定和高精度的相机标定方法，成为双目立体视觉领域重要的工作之一。

双目相机标定的本质是根据数学模型计算特征点三维空间坐标与二维图像坐标之间的投影关系［1～2］。工业应用中常见的标定方法多为张氏标定法及其改进算法［3～5］。张氏标定法是通过计算棋盘格角点的空间坐标与图像坐标的映射关系得到相机参数，其中角点的空间坐标已知，相机参数的标定精度就依赖于图像坐标系中角点的提取精度［6］。此方法主要存在两方面的问题，其一是在复杂背景中棋盘格角点提取不准确；其二是由于棋盘格标定板中心对称，左右图像中建立的图像坐标系可能不一致，导致同名特征点匹配失败。德国MVtec公司在软件HALCON中使用有方向标识的Halcon标定靶进行标定，利用圆形特征点代替棋盘格角点，提高了特征点的提取精度［7～8］。在实际应用中，相机需要从多个角度采集Halcon标定靶的图像，会使标定靶的圆形特征点投影到成像平面后变为椭圆特征点，而成像平面上椭圆特征点的中心与标定靶上对应圆形特征点圆心在成像平面上的投影并不重合，因此直接拟合椭圆中心点的方法存在误差，影响相机标定精度［9～10］。

为了克服上述缺点，文中提出一种基于Halcon标定靶感兴趣区域约束的透视变换的方法进行标定，能够从复杂背景中精确提取特征点的坐标，提高标定精度。方法包含了两个方面的创新点：一是，利用改进的角点提取算法从复杂背景中提取感兴趣区域，消除了复杂背景对特征点提取的影响；二是，通过对感兴趣区域透视变换，将椭圆特征点正投影到成像平面上，降低了直接拟合椭圆中心点的误差。

2 Halcon标定靶特征点提取及匹配

2.1 感兴趣区域提取

1）连通域角点粗提取

通过对Douglas-Peucker算法［12］改进来粗提取连通域角点，Douglas-Peucker算法的核心思想是曲线上的角点与参考直线之间的距离最大，且最大距离大于距离阈值，如图1中点P和点Q是曲线已知的两个端点，Wi是提取的角点。Douglas-Peucker算法只适用于提取已知端点的曲线上的角点，而闭合的连通域没有明确的起止端点，故对Douglas-Peucker算法改进：首先随机选择连通域上任意一点P和离P最远的点Q作为起止的两个端点，然后将连通域分为上下两部分，分别提取角点，如图2所示。

图1 Douglas-Peucker算法

图2 连通域角点提取图

2）干扰角点剔除

在粗略提取连通域角点过程中，由于随机的起止端点的引入和局部凸起像素的影响，会提取到干扰角点，如图2中点Wi是干扰角点，本文设计了一种方法剔除干扰角点。

定义dist(A，B)为两个点的距离，Δ(A，B，C)为线段AB与BC斜率差的绝对值，如式（1）。

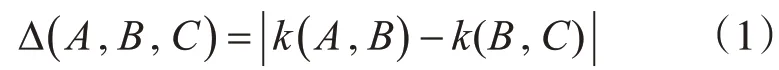
假设有n个待判断角点，真实角点之间最小距离为d，Δ(A，B，C)小于α则B点是干扰点，点Pi，Pj，Pj+1是迭代变量，则干扰角点剔除的方法步骤如下：

步骤1：若dist(Pi，Pj)＜d，则Pj是干扰角点，j+1后重复步骤1，否则执行步骤2；

步骤2：若Δ(Pi，Pj，Pj+1)＜α，则Pj是干扰角点，j+1后重复步骤1，否则点Pj是真实的角点，令i=j，j+1后重复步骤1，当j=n时执行步骤3，当j=n+1时执行步骤4，当j=n+2时结束判断；

步骤3：Pi不变，令j=n，初始点赋值给点Pj+1后执行步骤1；

步骤4：Pi不变，初始点赋值给点Pj，将第一个真实角点赋值给点Pj+1后执行步骤1。

3）感兴趣区域角点坐标确定

由于感兴趣区域是由5条直线围成的五边形，利用式（2）点到线的距离公式将轮廓点分为5部分分别表示五边形的每条边，用最小二乘法［13］分别拟合五条边的直线方程，最后用式（3）依次计算相邻边的交点，作为感兴趣区域的最终角点坐标。

式（2）中u、v是点的横纵坐标，直线的方程表示为直线Ax+B y+C=0。

式（3）中参与计算的两个边长方程分别是y=a1x+b1和y=a2x+b2。

2.2 特征点坐标拟合与匹配

1）特征点坐标拟合

空间中椭圆向相机成像平面投影时，相机坐标系与椭圆正交坐标系不重合，使得感兴趣区域内椭圆中心的真实投影点发生偏移，如图3所示，如果直接提取感兴趣区域内椭圆的中心坐标，椭圆中心图像坐标与其三维坐标不能准确对应［9］。

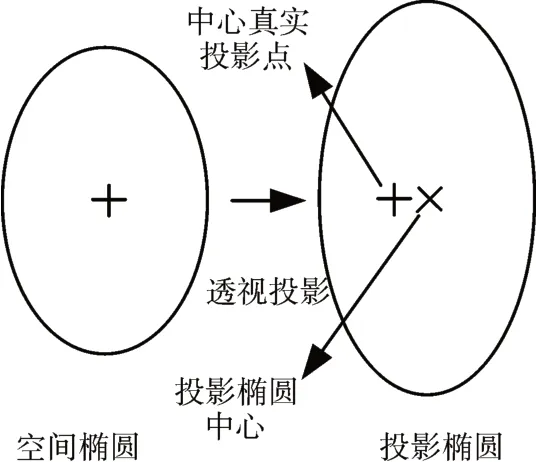
图3 空间椭圆中心的透视投影示意图

通过在提取椭圆中心坐标之前对感兴趣区域进行透视变换减小误差，记理想情况下感兴趣区域内一点为(u，v)，提取的与之对应点的坐标是(x，y)，则透视变换可以描述如式（4）。

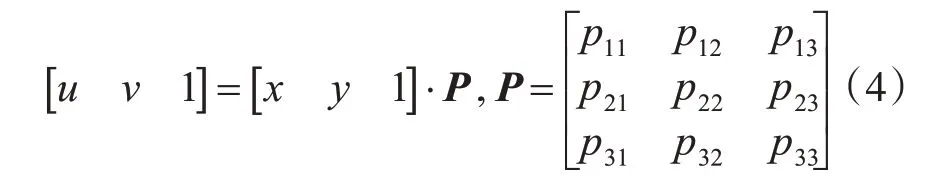
上式中P是透视变换矩阵，其中p33=1，利用理想情况下角点坐标和提取的角点坐标解P矩阵，然后对感兴趣区域透视变换并用最小二乘法拟合椭圆［14］得到椭圆的中心坐标。

2）特征点匹配

左、右图像的感兴趣区域经过透视变换后图像坐标系相同，可以通过计算特征点之间的最小距离匹配同名特征点，然后分别乘以左、右图像的透视变换逆矩阵P-1得到已匹配特征点的准确坐标。

综上所述，文中双目相机标定方法流程可总结如图4所示。

图4 双目相机参数标定流程图

3 实验结果与分析

3.1 实验环境及数据采集

为了验证本文方法精度，采用两台FLIR面阵CMOS相机构成双目立体视觉系统，其中相机镜头分辨率为2448像素×2048像素，像素尺寸为3.45μm×3.45μm，使用HC150-7.5，7×7型Halcon标定靶。结合OpenCV库图像处理函数和张氏标定原理，在VS 2017编程环境下编写标定程序，采集复杂背景中标定图像16组，如图5所示。

图5 16组标定图像

3.2 感兴趣区域提取与特征点拟合匹配结果

图6为利用本文方法对采集的图像进行处理得到的结果，其中图6（a）是在原图中提取的感兴趣区域角点，图6（b）是感兴趣区域的透视变换图。图7是感兴趣区域内特征点提取和匹配的结果图，左、右图中相同编号表示同名特征点。

图6 感兴趣区域

图7 特征点匹配

3.3 相机标定结果与分析

为验证本文特征点提取方法对双目相机标定精度的影响，使用本文方法和文献［8］中基于HALCON的标定方法分别利用图5中的16组图像进行双目相机参数标定，并在相同背景下采集16组GP260-9*9棋盘格标定板图形，利用文献［15］中基于张氏标定的方法对双目相机进行参数标定，标定结果保留小数点后四位，如表1所示。

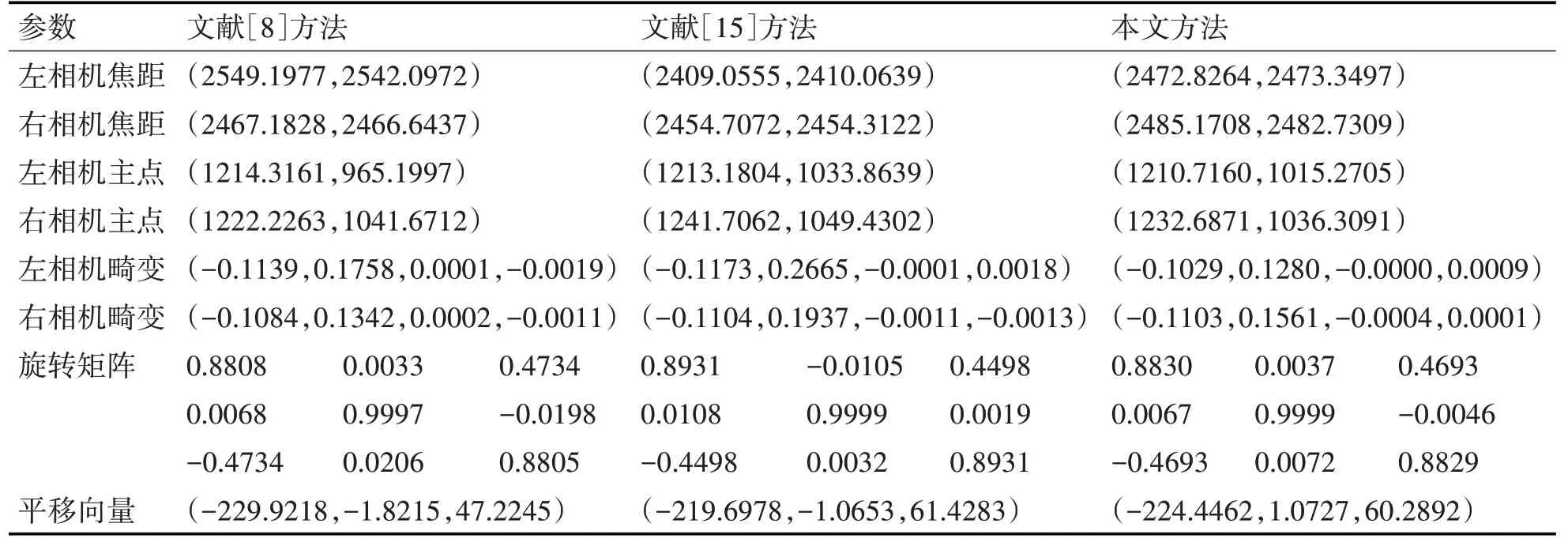
表1 相机参数标定结果

通过重投影法对文献［8］、文献［15］和本文方法的标定结果进行评估。利用表1中双目相机参数标定的结果，计算可得每幅图像中特征点平均重投影误差如图8所示，其中编号1～16的数据表示左图像，编号17～32的数据表示右图像。

图8 重投影误差图

对图8中的32幅图像特征点平均重投影误差再平均可得文献［8］、文献［15］和本文方法的整体平均投影误差分别是0.03像素、0.04像素和0.01像素，对比可知利用本文方法标定取得的结果优于文献［8］和文献［15］的方法，特征点平均重投影误差更小，精度更高。

4 结语

本文主要研究双目相机参数的标定，针对在复杂背景中传统相机标定方法对特征点提取不准确，导致相机标定精度不高的问题，提出一种基于Halcon标定靶感兴趣区域约束的透视变换方法，能够从复杂背景中精确提取特征点坐标。通过改进的角点提取方法获取Halcon标定靶上的感兴趣区域，消除背景对特征点提取的影响；通过利用透视变换将椭圆特征点正投影到成像平面上和最小二乘法椭圆拟合降低特征点坐标的提取误差；然后匹配同名特征点并使用张氏标定原理计算双目相机的参数。对比传统标定方法在复杂应用场景中的标定精度，实验结果表明，本文的标定方法重投影误差更小，标定精度更高。