构造几何图形 巧解向量问题
——以近几年浙江省高考试题为例
2022-05-09 02:33葛桂
高中数学教与学 2022年7期
葛 桂
(浙江省东阳中学,322100)
向量问题既具有数的特征——运算,更具有形的本质——几何意义,这也为我们的解题提供了不同的视角.在众多的高考题中,浙江卷中的向量题一向以几何背景清晰,构思巧妙、设问新颖、解法多样著称,为中学教师所青睐.本文以近几年浙江高考卷客观题中的向量压轴题为例,阐述如何构造图形巧解向量问题.
例1(2021年浙江高考题)已知平面向量a,b,c(c≠0)满足|a|=1,|b|=2,a·b=0,(a-b)·c=0.记向量d在a,b方向上的投影分别为x,y,d-a在c方向上的投影为z,则x2+y2+z2的最小值为______.
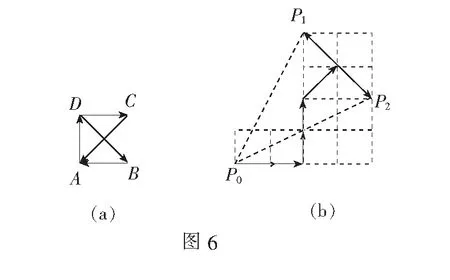
分析本题可从a·b=0,(a-b)·c=0给出的垂直关系出发构造图形进行解题.
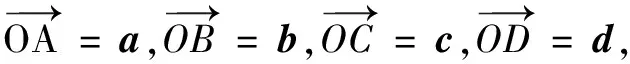
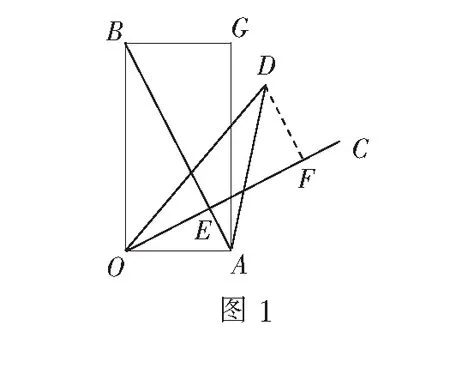
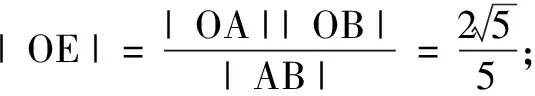
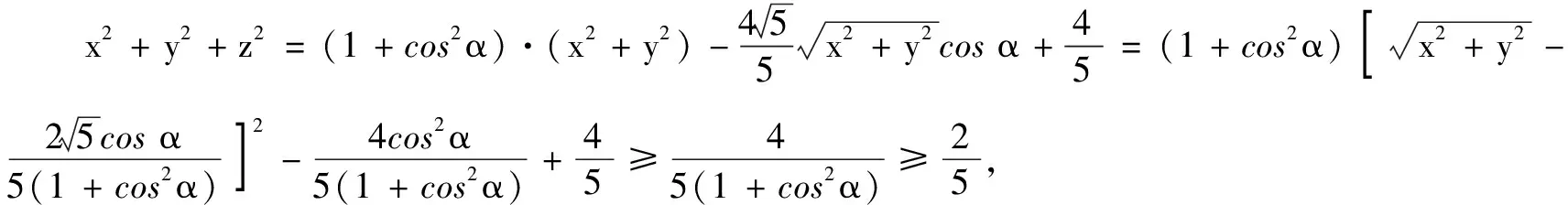
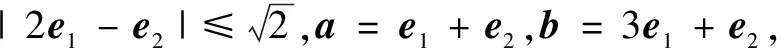
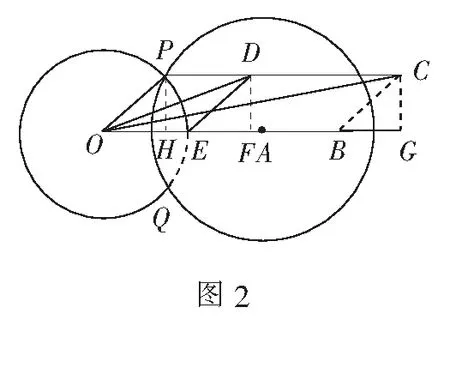
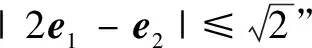
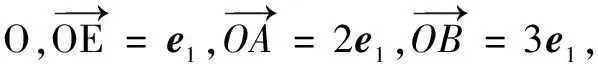
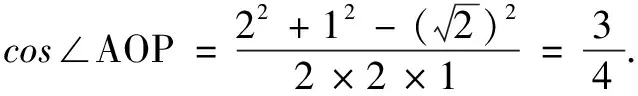
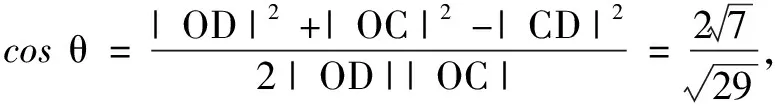
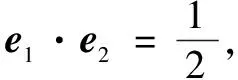
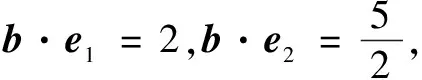
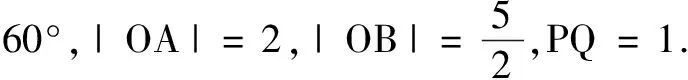
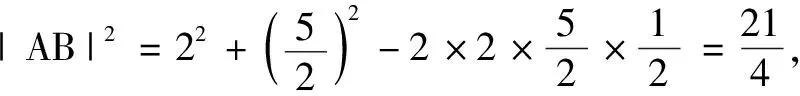
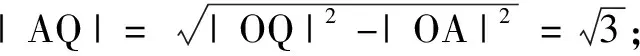
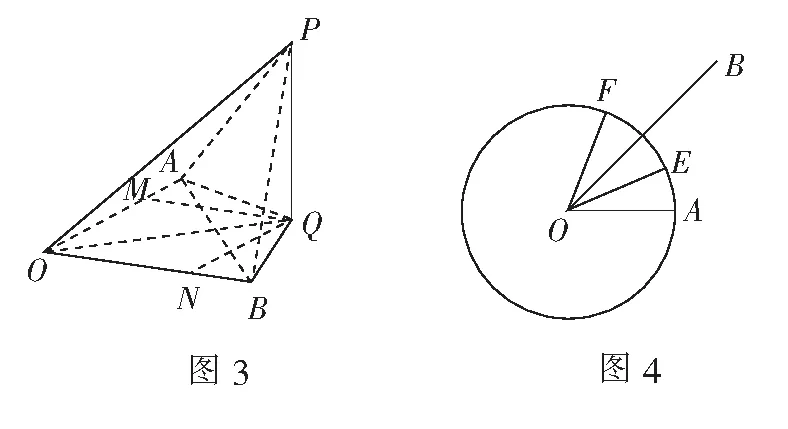
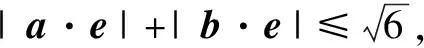
分析显然当向量a,b的夹角α为锐角时,a,b可取得最大值,因此在构造图形时不妨设a,b的夹角α为锐角.
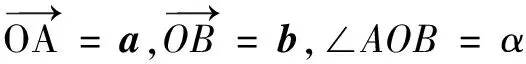

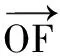
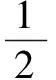
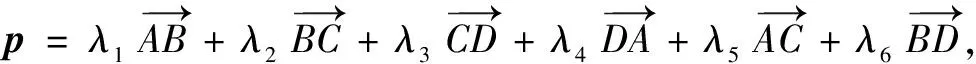

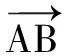
猜你喜欢
中学生数理化(高中版.高考理化)(2022年2期)2022-04-26
中学生数理化(高中版.高二数学)(2021年9期)2021-11-05
中学生数理化(高中版.高考理化)(2021年5期)2021-07-16
中学生数理化·高一版(2020年11期)2020-12-14
中等数学(2020年4期)2020-08-24
中学数学杂志(2019年1期)2019-04-03
数学大王·中高年级(2019年2期)2019-01-23
新世纪智能(数学备考)(2018年9期)2018-11-08
高中生·天天向上(2018年1期)2018-04-14
小学生学习指导(中年级)(2017年4期)2017-03-20

