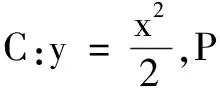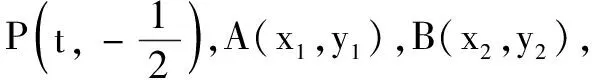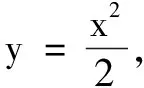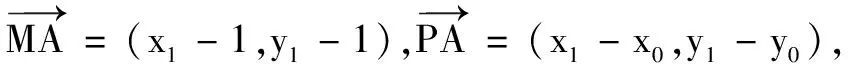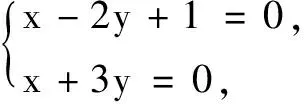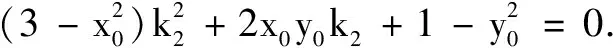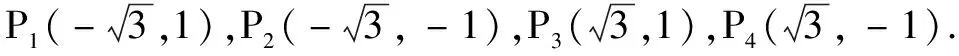例谈同构思想在数学解题中的应用
卢恩良
(江西省九江市第三中学,332000)
一、在数列中的应用
数列递推技巧的核心本质是同构,对于等差、等比型的数列问题,利用所给递推公式依序同构,是解题思路形成的理论依据.
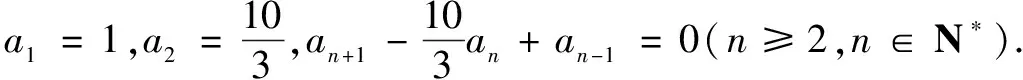
(1)若数列{an+1+λan}是等比数列,求实数λ;
(2)略.

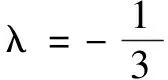
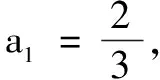
(1)证明:{bn}是等差数列;
(2)略.
解由bn=3nan,要证{bn}是等差数列,只要证3n+1an+1-3nan为常数.由3n+1an+1与3nan结构相同,为了配出3n+1an+1,对条件等式两边同乘以3n,得3n+1an+1=3nan+1,即3n+1an+1-3nan=1,所以{bn}为等差数列.
例3若数列{an}满足a1=1,nan+1-(n+1)an=0(n∈N*),求数列{an}的通项公式.


评注比较可见解法2显得简洁高效,这就是同构思想的威力所在.
二、在方程中的应用
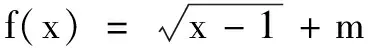
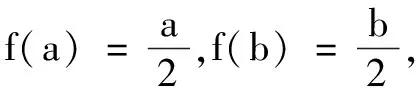
例5已知x,y∈R,且满足(x-1)5+2x+sin(x-1)=3,(y-1)5+2y+sin(y-1)=1,求x+y的值.
解观察发现两个方程左边结构相同,但单个方程中的变量x和y结构并不一致,因此考虑将题设方程化为
设h(x)=x5+2x+sinx,则h(x-1)=1,h(y-1)=-1.因为h(x)为奇函数,所以h(x)+h(-x)=0.又h′(x)=5x4+2+cosx>0,h(x)为增函数, 结合h(x-1)+h(y-1)=0,得x-1+y-1=0,即x+y=2.
例6已知x0是方程x2ex-2+lnx-2=0的一个根,求e2-x0+lnx0的值.
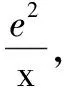
评注同构思想在方程中的应用,往往会和函数的单调性与奇偶性一起考察.当遇到含有指数和对数结构的方程时,需要灵活运用指数对数运算公式.
三、在不等式中的应用
在遇到含有双变量的不等式问题时,利用同构思想将不等式两边化为结构相同的两部分,再结合函数的性质处理,往往能达到意想不到的效果.
例7(2020年全国高考题)若2x-2y<3-x-3-y,则( )
(A)ln(y-x+1)>0
(B)ln(y-x+1)<0
(C)ln|x-y|>0
(D)ln|x-y|<0
解依题意,2x-3-x<2y-3-y,观察不等式两边结构一致,可设h(x)=2x-3-x,则h(x)
变式1(2020年全国高考题)若2a+log2a=4b+2log4b,则( )
(A)a>2b(B)a<2b
(C)a>b2(D)a 提示方程同构变形得2a+log2a=22b+log2b.设h(x)=2x+log2x,利用h(x)单调增及log2b 综上,可得m≥1. 含有参数的不等式成立问题是高考的热点和难点问题. 求解此类问题有时候采用分离参数法或分类讨论,难度较大,甚至无法将变量分离出来,但如果利用同构思想考虑,能使解题难度大大降低. 例8(2020年全国高考题)已知函数f(x)=aex-1-lnx+lna. (1)略; (2)若f(x)≥1,求a的取值范围. 解因为f(x)=eln a+x-1-lnx+lna,故由f(x)≥1可得eln a+x-1+lna-1≥lnx,即eln a+x-1+lna+x-1≥lnx+x,亦即eln a+x-1+lna+x-1≥eln x+lnx. 设h(x)=ex+x,则h(lna+x-1)≥h(lnx).又h(x)为增函数,故lna+x-1≥lnx,即lna≥lnx-x+1.由导数法易知函数φ(x)=lnx-x+1(x>0)的最大值是φ(1)=0.所以lna≥0,得a≥1. 变式若2ae2x-lnx+lna≥0恒成立,求a的取值范围. 同构思想在解析几何中的应用也非常广泛,尤其是在处理双切线问题时,堪称“解几利器”. 变式(2020年全国高考题改编)已知圆M:(x-1)2+(y-1)2=4,直线l:2x+y+2=0,过l上动点P作圆M的两条切线PA,PB,切点为A,B.求证:直线AB过定点. 同理,由MB⊥PB,可得(x2-1)(x0-1)+(y2-1)(y0-1)=4.于是点A(x1,y1),B(x2,y2)都满足(x-1)(x0-1)+(y1-1)(y0-1)=4,即直线AB的方程为(x-1)(x0-1)+(y-1)(y0-1)=4. 综上,点P的轨迹方程为x2+y2=4. 总之,利用同构思想解题,不仅需要有同构意识,还要善于观察和对代数式的变形能力.运用同构思想解题技巧性较强,对综合能力要求较高.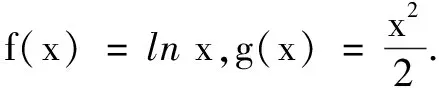
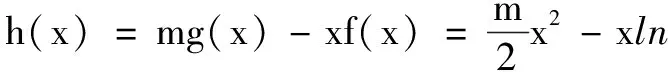

四、在函数与导数中的应用
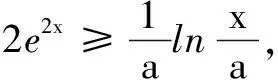
五、在解析几何中的应用