一次生成性课堂的教与学

湖北 冯爱龙

新课程背景下生成性课堂是教学的亮点，它解放了教师、学生和教材，使课堂教学焕发出生命活力；生成性也是新课程背景下的课堂教学难点，课堂“开放了”“生成了”，就可能出现“无序”的状态，这就给教师带来了挑战，很难预测教学目标的达成度.教师在面对“节外生枝”的课堂突发事件时，要客观、准确地评价学生“意外”的思维方式与解题方法，因地制宜改变原来的教学计划，让数学课堂更具“动感”，使得不可预测的课堂“意外”更好地激发学生的思维、演绎新的情形，并成为学生掌握学科知识技能、提升核心素养的增长点.下面笔者结合一节习题课的片断教学，谈谈课堂教学应急处理的心得体会.

一、真题呈现

题目：如图，已知点C的坐标是(2，2)，过点C的直线CA与x轴交于点A，过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点，求点M的轨迹方程.

二、真题破解

1.预料之中的“一题多解”

分析：教师引导学生依据条件画出图形，分析题意，学生积极回应，讨论归纳出如下四种途径:

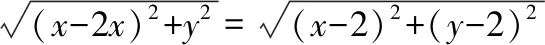
生2(定义法)：观察出“Rt△ACB与Rt△AOB有公共的斜边AB”这个隐含条件，根据平面几何知识得|MO|=|MC|，即点M的轨迹就是线段OC的垂直平分线，由点斜式方程得所求方程为x+y-2=0.

前三种解法学生都感觉到“平面几何味道”很浓,需要运用平面几何知识等价转化；后一种解法主要是用参数方程的思想,学生接触很少,没有可以模仿的例题,独立解决有困难,需要教师的铺垫与归纳.实际上以上四种解法都是解决此类问题的通性通法，基本符合学生的认知与思维水平，当然也是教师备课时首先要准备的，预设通过题组训练来巩固与强化，进行归纳总结与推广.课堂教学按既定方案和流程继续运行.

2.突如其来的“节外生枝”

具有鲜明主观能动性的学生，作为一种活生生的力量，往往是带着自己的知识、经验、思考、灵感与期盼参与课堂教学活动.当同学们正忙于欣赏上述四种通法时，有一位同学提出一种新的解法，用初中平面几何知识通过作辅助线，将点的坐标与线段的长度相互转化，最终建立动点M的坐标满足的方程.于是就请该生上讲台在黑板上展示他的解答过程：

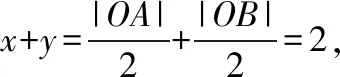
当其他同学正在为他的精妙解法叫彩时，又有一位同学站起来.他说上述解法只考虑了点M在第一象限这一特殊情形，显然思维不严谨.

叶圣陶先生说“教师之为教，不在全盘授予，而在相机诱导”.为了进一步激发学生的思维热情与探究欲望，于是就临时放弃了原来既定的教学预设，组织学生继续讨论并完善此解法的后续过程.

师：以上两位同学接力使这道题得到较为完美的解答，既训练了学生的思维严谨性，又培养了学生的合作意识.对照前面几种做法，这种解法显然较为烦琐，请同学们讨论“造成这种烦琐的原因是什么？”

生7：这种解法是想通过几何推理论证将点的坐标转换成相应线段长度，建立起点M的坐标所满足的方程.但随着图形的变化，点的坐标与线段的长度并不总是相等的.因此要分类讨论，也就显得烦琐些.

学生在初中进行了大量的平面几何推理训练，对解析几何所倡导的几何问题代数化的思想与方法并没有深刻体会，遇到几何问题很容易按惯性思维习惯去思考或分析.通过上述几位学生的解法比较，让学生从中深刻体会到坐标法在解决此类问题中的优越性，从而对解析几何思想方法有了实践上的认识.对于此类问题的解法，通过学生们的相互讨论、补充，本节课的教学任务与目标基本达成，对笔者而言临场及时调整教学设计无疑是一次成功的被动尝试.在准备进行课堂训练与总结提升的教学环节时，一个新的意外发生了……

3.一波又起的“合作探究”

生8：如果把刚才同学的解法与坐标法结合起来考虑，怎么求出的曲线方程有两个呀？

师：说说自己的思考，我们一起来分析.

一时间教室里炸开了锅，全班同学被这个结论给惊住了.如果说刚才的“节外生枝”令人“小吃一惊”，这位同学的解法和结论真是“石破天惊”.这时候教师就要耐心引导学生明确问题的真正症结——“眼见为实”，应该让事实说话，让孩子们自己说服自己，这样他们认识问题的角度才会更全面，理解题意的思维也会更严谨.

师：如果这位同学所求的点M的轨迹方程真的有两条，那么前面四种方法都出问题了吗？如果求得的方程x-y=0是多余的，那么这个结论又是从何而来的呢？

学生又陷于思考与讨论之中，几分钟后，又有一位同学站起来发言.

生10：上述解法是误看条件了，以为△ABC是等腰三角形，并利用等腰三角形的性质构造出相应的坐标等式.但题目条件并不能保证“△ABC是等腰三角形”，实际上所求得的轨迹方程x-y=0也不满足“CA⊥CB是直角”这个条件.如果检验一下，也能发现这个问题.可见求动点的轨迹方程时“第五步检验”环节还真不能少，难怪老师反复强调曲线方程的概念和求解步骤，以后同学们可真得注意了.

这节课就在一波未平一波又起的探究互动过程中结束了，虽然题组训练没能展开，但由于及时转变教学流程，对学生的思维因势利导，整节课学生的思维活跃起来了，探究积极起来了.正如赞可夫所说“教学法一旦触及学生的情绪和意志领域，触及学生的精神需求，这种教法就能发挥高度有效的作用”.正所谓“失之东隅，收之桑榆”，通过引导使学生感受到坐标法解轨迹问题的优越性，深化了对曲线与方程之间的内在联系的理解，未尝不是一种更大的收获.

三、反思感悟

1.教学设计是教师通过自身认知对教材内容的谋划与建构，既需要直面课堂和学生，又不能被教材所局限，是一个不断探究、思考、学习和实践的动态推进过程.本节课的设计由一道常规的习题引入，呈现出“低起点、高立意、深互动、活思维”的教学生态，虽然在教学过程中出现了诸多“意外”，打乱了课前预设程序和教学内容，逼迫自己“忍痛”放弃教学预设，但是通过有深度、有力度的理性思维延展教学，整合初高中数学思想方法，引导学生深度探究和提炼解题方法，让师生在思维碰撞中不断生成智慧的火花，提升了学生的数学核心素养和思维层次.也让笔者对数学知识的理解和体系建构方式、学情的认知与课堂生成状态都有了全新的认识，深刻体会到备课不能拘泥于课本与资料，要敢于质疑、不迷信权威，要善于运用数学的思维提出自己的不同见解、多维度思考，这些正是数学核心素养的体现.教师还要善于把握课堂教学动态，用心捕捉、及时搜集、有效筛选学习活动中瞬间的生成，让学生在动态生成中得到全面、健康的发展.

2.重视学生在学习过程中的思维和能力发展，关注学生的过程性“错误”，将课堂中自然生成出来的“意外”作为新的教学资源，引导学生学会多问几个“为什么”，学会质疑、答疑，敢于尝试、变式，教会学生挖掘知识背后蕴藏的数学思想方法，增强对未知领域的探索与深化.通过教师机智巧妙地引导与运用，使之“化腐朽为神奇”，成为课堂的另一种精彩.轨迹方程的求解或轨迹的确定是平面解析几何中的一个基本问题与热点问题，在教学中要结合经典真题，通过合理的分析、研讨、借鉴与应用，进行多视角思考、变式、拓展、总结与归纳，从而借题发挥，探索破解问题的一般性规律与策略，真正达到“做一题，通一类，会一片”的“以小见大”的教学目的，减少“题海战术”解题式教学，让学生积极、主动地投入到课堂学习中去，使教与学的过程充满挑战与活力，达到数学核心素养自然提升的境界.本节课后半场在学生主动思考、大胆质疑的互动中达到思维最强磁场的效果，通过不断追问、解疑促发学生的质疑和反思，让学生自然生成一串串“念想”，激发学生的“愤”与“悱”，促进学习的深入，深化学生的思维品质.