大单元视角下构建题组深度复习的教学实践与反思——以“立体几何解答题专题复习教学”为例

广东 潘敬贞 骆妃景

1.授课背景

本节课是笔者开展基于核心素养的高中数学深度教学模式研究，探究“大单元复习”课堂变革的一节复习型展示课，大单元视角下构建题组深度复习是把相关联的知识和方法，通过题目精心设置和顺序编排，变成一系列问题或题组，题组中的试题由易到难，由单一到综合，呈现递进关系，螺旋上升，突出一题多变，展示数学问题的可变性，将章节基础知识、基本技能、基本方法和基本思想连成线，织成网，铺成面，以题组驱动复习，提高学生的数学核心素养和课堂复习效率.本文将教学过程做一整理与各位同行交流探讨.

2.教学构思

立体几何是高中数学的核心内容，是培育学生直观想象核心素养以及厚植学生理性精神的沃土，也是培养学生养成懂理讲理良好习惯的绝佳素材.立体几何是历年高考考查的重点内容，利用空间向量解决立体几何问题是高二第一学期重点学习的内容，也是高二第一学期期中考试重点考查内容，立体几何解答题也是高考必不可少的试题.

因此，在二轮复习中对相关知识进行回顾复习是很有必要的,然而，时间紧迫，内容多，任务重，迫切需要一种复习模式来提升考前复习效率，大单元视角下构建题组深度复习则提供了一种有效思路.

立体几何解答题主要以常见几何体为载体，结合空间向量工具，考查立体图形中的线线、线面和面面位置关系及数量关系.试题的第一问主要考查线线垂直、线面平行、线面垂直、面面垂直的求证为主；第二问主要考查线面夹角、点面距离、面面夹角、几何体的体积等问题，主要考查学生逻辑推理、数学运算与数学建模等数学核心素养.因此本节课的教学设计重点是通过结合常见的几何体，梳理常见的建立空间直角坐标系的策略，归纳总结求证线面平行、线线垂直、线面垂直、面面垂直的思想方法，求解线面夹角、点面距离、面面夹角等问题的求解思路和解题思维痛点.以“问题解决”贯穿始终，设计层层递进的题组，让学生在教师的引导下分析问题、解决问题，使得章节知识方法系统化，发展直观想象、逻辑推理、数学运算等数学核心素养.

3.教学过程

3.1 以任务为驱动，促进回顾复习

【问题1】如图，四棱锥P-ABCD，底面ABCD是平行四边形，M，N分别是PC，AB的中点，过AP作平面APGH交平面BDM于GH，求证：

(1)AP∥平面BDM；

(2)MN∥平面PAD；

(3)AP∥GH.

设计意图:问题1试题难度较低，第(1)问只需通过连接AC即可构造三角形的中位线，从而证明线面平行；第(2)问是取PD中点通过构造平行四边形来证明线面平行；第(3)问是在第(1)问的基础上进一步利用线面平行的性质来证明线线平行.问题1的3个问难度都比较低，但低起点能够很好地激发学生的学习兴趣，在问题解决中提高学生自我效能感，回顾复习线面平行的判定定理和性质定理，回顾复习证明线面平行的一般方法(中位线法和构建平行四边形法)，进一步深化知识的理解和方法的应用.

【问题2】如图，在三棱柱ABC-A1B1C1中，AB⊥平面BB1C1C，且四边形BB1C1C是菱形，证明：AC1⊥B1C.

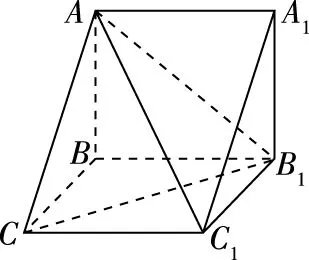
【变式1】在三棱柱ABC-A1B1C1中，四边形AA1B1B是矩形，平面AA1B1B⊥平面BB1C1C，四边形BB1C1C是菱形，求证：AC1⊥B1C.

变式1只将问题2已知条件中的AB⊥平面BB1C1C改为平面AA1B1B⊥平面BB1C1C，利用面面垂直的性质定理转化为直线垂直于平面，虽然只做微小的改变，但更有利于学生掌握证明有关垂直关系的解题套路和平面垂直平面的性质定理的内涵.

【变式2】在三棱柱ABC-A1B1C1中，四边形BB1C1C是菱形，∠ABB1=∠ABC，求证：AC1⊥B1C.

变式2是将问题2已知条件中的AB⊥平面BB1C1C改为通过已知∠ABB1=∠ABC先证明△AB1C为等腰三角形，再利用等腰三角形三线合一性质得到AB⊥B1C，相对于问题2和变式1，题目条件更加隐蔽，更有利于制造思维的冲突，对调动学生学习积极性，创造合作学习、互动交流的氛围和机会，提高学生分析问题和解题能力都有很好的帮助.

变式3是想切换另外一个角度，将问题2已知条件中的AB⊥平面BB1C1C改为已知图形元素的数量关系，通过运算和利用正弦定理得到线线垂直的结论，因此在证明有关垂直问题时可以考虑空间中直线与平面的位置关系和数量关系，由此拓宽学生思考问题的角度，提高学生的应变能力，审题提取信息的能力和解题能力.

通过问题2以及变式1，2，3的分析与证明，学生可以熟悉掌握以菱形、直线与平面垂直、等腰三角形、勾股定理的逆定理、平面与平面垂直等为素材证明直线垂直于直线乃至有关垂直问题的解题套路.

【变式4】在三棱柱中ABC-A1B1C1，AB⊥B1C，四边形BB1C1C是菱形，求证：AC=AB1.

变式4是将问题2中的问题，求证：AC1⊥B1C改为求证AC=AB1，这样题目的目标就相对更具隐蔽性，解决这个问题就需要将目标转化为一系列相对较为复杂的过程，可以将学生的学习思维强度、课堂合作学习、互动交流的气氛等推向高潮，有效地培养学生的应变能力与创新思维，提高学生的解题能力，提升学生的数学综合能力等.

【变式5】在三棱柱ABC-A1B1C1中，AB⊥平面BB1C1C，且四边形BB1C1C是菱形，求证：平面ABC1⊥平面AB1C.

变式5做了一个温和的变式，将问题2中的问题，求证：AC1⊥B1C改为求证平面ABC1⊥平面AB1C，改变问题视角，强调空间转化，解答过程又回到起点.这样利于反思总结本节课学习的内容，促进教学目标的达成.

设计意图：问题2的主要目的是让学生在对问题的求解过程中回顾复习立体几何中有关垂直证明问题，梳理有关垂直证明问题的构建要素和一般求解思路以及规范表达.激发学生通过问题与变式螺旋上升的分析与解决过程中复习内化已学知识和方法的热情.

【问题3】如图，已知四边形ABCD是直角梯形，∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=2，AD=1，试建立适当的空间直角坐标系.

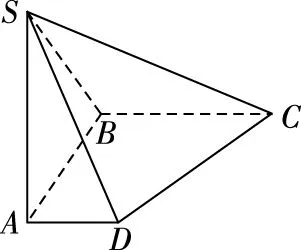
(1)求平面ABCD的一个法向量；

(2)求平面SAB的一个法向量；

(3)求平面SAD的一个法向量；

(4)求平面SBC的一个法向量；

(5)求平面SBD的一个法向量；

(6)求平面SCD的一个法向量；

(7)求BC与CD所成角的余弦值；

(8)求点B到平面SCD的距离；

(9)求直线SB与平面SCD所成角的正弦值；

(10)求平面SAD与平面SCD所成角的余弦值.

设计意图：问题3是以直角梯形为底面，线面垂直为载体，要求学生建立合适的空间直角坐标系，求平面的法向量，利用向量解决异面直线夹角、线面夹角、二面角、点面距等常见问题.本道试题直接已知三条共点且两两互相垂直的直线使得空间直角坐标系容易建立，提出的问题也很基础，问题呈现层层递进，螺旋上升.学生通过简单复习可以顺利解答本道试题，同时回顾立体几何解答题常考的问题，引导学生逐渐构建知识体系，使知识系统化、网络化.

3.2 换问题情境，夯实四基，提升四能

(1)求证：平面EAC⊥平面FAC；

(2)求直线BC与平面AEF所成角的大小.

【解析】(1)设AC∩BD=O,利用面面垂直的性质、线面垂直的性质及等腰三角形中线性质得到AC⊥EO，再利用勾股定理及勾股定理的逆定理证明EO⊥OF，由线面垂直的判定定理得到EO⊥平面FAC，最后由面面垂直的判定定理得到平面EAC⊥平面FAC；

(2)解法一：如图，延长CB到点H，使得BH=BC，连接AH，FH，易知四边形AEFH为平行四边形，故A，E，F，H四点共面，所以直线BC与平面AEF所成的角.即直线HC与平面AEFH所成的角.

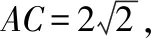
因为EF∩AG=G，EF，AG⊂平面AEFH，所以CG⊥平面AEFH.

连接HG，则∠CHG即直线BC与平面AEF所成角.在Rt△HGC中，CG=2，HC=4，

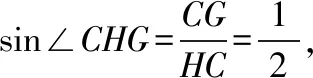
解法二：取EF的中点G，连接OG，易知OA，OB，OG两两垂直，故以O为坐标原点，OA，OB，OG所在直线分别为x，y，z轴建立如图所示的空间直角坐标系，

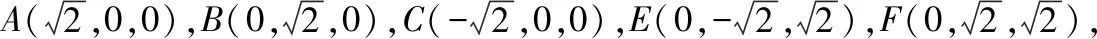
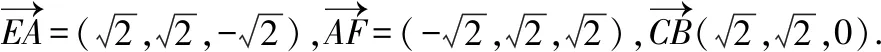
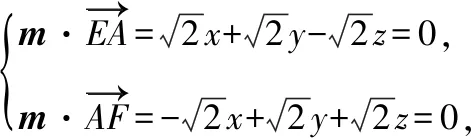
所以直线BC与平面AEF所成的角为30°.

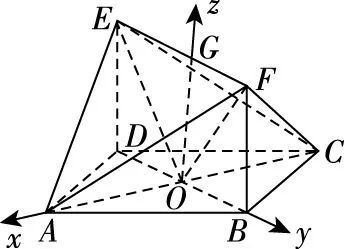
设计意图：问题4以正方形和面面垂直为问题情境，学生可以快速找到三条共点且两两互相垂直的直线即可建立空间直角坐标系，同时提出面面垂直和线面夹角问题，第(1)问学生利用立体几何中相关定理、性质解决问题，第(2)问则用向量工具解决问题，学生进一步熟悉相关知识和问题的求解思路.

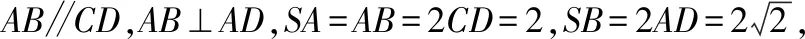
(1)求证：CE∥平面SAD；

(2)求证：BD⊥平面SAC；

(3)求直线CE与平面SAC所成角的余弦值.

设计意图：问题5结合勾股定理的逆定理证明线线垂直，进而建立空间直角坐标系，并解决常规的立体几何问题，通过问题5的求解进一步提升学生建立空间直角坐标系与解决问题的能力.

【问题6】如图1，已知△ABC是边长为6的等边三角形，点D，E分别是边AB，AC上的点，且满足AD=CE=2，如图2，将△ADE沿DE折成四棱锥A1-BCED，且有平面A1DE⊥平面BCED.

图1

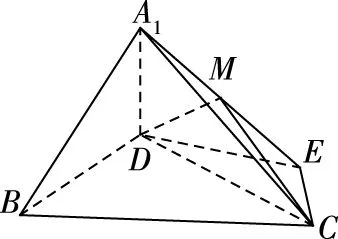
图2

(1)求证：A1D丄平面BCED；

(2)记A1E的中点为M，求二面角M-DC-A1的余弦值.

设计意图：问题6是以翻折问题为载体，结合面面垂直作为问题情境，设置线面垂直和二面角问题.问题情境和提出的问题都是学生熟悉的问题，学生在老师的引导和生生互动交流中很快就能找到解决问题的突破口.

(1)若M是AB的中点，N是棱PC上一点，且CN=2PN，求证：MN∥平面PAD；

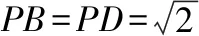
【解析】(1)如图，连接CM并延长，交DA的延长线于点E，连接PE.

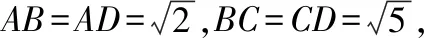
所以△ADC≌△ABC，所以∠ACD=∠ACB，

所以△DOC≌△BOC，所以DO=BO，∠COD=∠COB=90°.

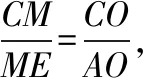
因为AB⊥AD，所以OA=OB=OD=1，易得OC=2，所以CM=2ME，又CN=2PN，所以MN∥PE，

因为PE⊂平面PAD,MN⊄平面PAD，所以MN∥平面PAD.

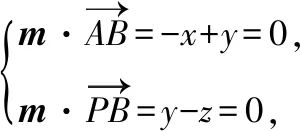
令x=1，则y=1，z=1，所以平面PAB的一个法向量为m=(1,1,1).

令x1=1，则y1=-2，z1=-2，

设计意图：通过问题1,2,3的求解，学生回顾复习了立体几何解答题中的相关知识和求解思路，经过对问题4,5,6的分析与交流，学生进一步熟悉立体几何解答题的常规问题的求解思路，提升运算求解能力，此时给出问题情境相对复杂，试题难度有所提升的问题7，在老师的引导以及与同学们的交流中，学生受到启发，完全能找到解决问题的突破口.

3.3 全面提升数学能力，发展数学核心素养

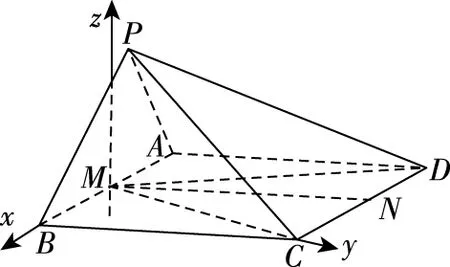
(1)求证：CM⊥平面PAB；

【解析】(1)先证明CM⊥AB，然后连接PM，利用题目所给的边长关系，根据勾股定理证明CM⊥PM，然后根据线面垂直的判定定理即可得到CM⊥平面PAB；

平面PMD的一个法向量为m=(x1,y1,z1)，直线PN与平面PMD所成角为θ.

【评析】本题考查线面垂直的证明及空间中的探索性问题，一般地，对于探索性问题的解答方法如下:

(1)可先假设所求的点存在，合理设元；(2)然后建立空间直角坐标系，标出各点的坐标，求出直线的方向向量、平面的法向量等；(3)结合已知条件列出有关线面夹角、面面夹角成立的含参方程；(4)解方程，得出参数的值即可.

【问题9】如图，四棱锥P-ABCD的底面为菱形，且∠ABC=60°，PA⊥平面ABCD，M为BC的中点.

【评析】利用空间向量计算二面角的常用方法：1.法向量法：分别求出二面角的两个半平面所在平面的法向量，然后通过两个法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角的大小；

2.方向向量法：分别在二面角的两个半平面内找到与棱垂直且垂足为起点的两个向量，则这两个向量的夹角的大小就是二面角的大小.

设计意图：问题8的第二问和问题9的第一问都采用探究性设置问题，有很浓的探究味道，有很好的开放性，对学生辩证思维和逻辑推理以及运算求解能力都提出了更高的要求，对培育学生的理性精神和创新意识有重要意义.问题9的第二问通过已知二面角得到点的位置，进而求几何体的体积和异面直线夹角问题，问题有一定的灵活性，但归根结底还是二面角问题，必经过建立空间直角坐标系利用空间向量解决问题，通过对这两道题的求解进一步提升学生分析问题和解决问题的能力.

【问题10】如图，已知直三棱柱ABC-A1B1C1中，侧面AA1B1B为正方形，AB=BC=2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF⊥A1B1.

(1)证明：BF⊥DE；

(2)当B1D为何值时，平面BB1C1C与平面DFE所成的二面角的正弦值最小?

设计意图：问题10是通过设参数，并利用二次函数或基本不等式解决最值问题，试题具有较高的综合性，问题的求解对学生的数学综合能力要求也比较高，对训练学生数学思维和提升学生的分析问题和解决问题的能力具有重要意义.

4.几点思考

大单元视角下构建题组深度复习避开常规复习课讲题做题的套路，用题组串联已学知识，形成更完整的知识脉络，让复习课更有新意.深度复习过程的核心是设置层层递进，螺旋上升的题组，指向大单元深度复习的高效题组设计有哪些显著的特征呢？

4.1 以问题驱动复习为构建题组的逻辑起点

问题是数学的心脏，思维从问题开始，创设合适的问题情境，以问题引领学习，启发学生思考，翻阅教材、笔记本等，自主梳理基本知识、基本思想方法.本课例题组一为问题1至问题3突出一题多变，一题多问，主要设置常规且简单的问题情境，提出常规且简单的数学问题.问题指向清晰明了，学生可以直接读懂题意.因此笔者将题组一作为课前任务单让学生在课前自主完成解答，然后收取课前任务单并检查学生完成情况，同时与部分学生当面交流，听取学生感想和意见.笔者发现，在此之前绝大部分学生对立体几何解答题的一些常见问题和求解思路已经遗忘，但通过题组一的任务驱动，学生能够自主翻阅教材和笔记，能够很快回忆起相关知识以及常见问题的求解思路.由于题组一试题难度不大，起点较低，问题较为直接、单一，学生能够顺利解答问题，通过题组一的求解学生基本能够实现回顾复习立体几何的基本概念、基本知识，平面法向量的求解，归纳梳理求证线面平行、线线垂直、线面垂直、面面垂直的基本思想方法，求线线夹角、线面夹角、点面距离、面面夹角的思路与步骤等已学内容.学生在完成课前任务单过程中没有较大心理压力，而且感到较为轻松、愉快.课堂上让学生上台展示，学生相互交流，教师点评，课堂气氛活跃，取得很好的教学效果，达到预期的目的，为下一环节(题组二)的学习奠定了坚实的基础.

4.2 构建不同的问题情境促进学生自主构建

题组二为问题4至问题6，提供了思维生长点，构建了认知结构的固着点，设置了不同情境的问题来驱动学生加深对基本知识、基本思想方法的理解，着重培养学生在不同问题情境(几何体)中快速寻找到(或作)三条共点并两两互相垂直的直线，然后建立空间直角坐标系，求出相应点的坐标和所需的向量，归纳常见几何体的建系策略，厘清常见问题的求解思路，训练学生的规范表达.经历了题组一的展示与交流之后，很多学生信心满满、胸有成竹，课堂气氛活跃.此时笔者先让学生分析题组二的建系思路，寻找最优的建系方法(尽可能地使得更多点落在坐标轴上或在轴面上)，并说出自己的想法，学生发言踊跃，然后将学生分组进行动手解决问题，并派代表展示本组的学习成果.在整个过程中学生动作迅速，得到充分表达，师生和生生间充分交流，取得很好的教学效果.整个课堂以环环相扣的问题串来推进复习，在求解问题过程中生生交流、师生交流中相互促进，进一步激发学生独立思考，自主构建，发展数学核心素养.

4.3 构建题组应注重学生的思维能力的发展