从一道高考真题反思高考命题与备考

甘肃 陈鸿斌

本文通过对2021年全国乙卷理科第9题进行探究,分析了高考创新试题的特点和命题趋势,进而反思高三二轮复习中的应对策略,为一线课堂教学与测评考试提供参考.

1.真题呈现

(2021·全国乙卷理科·9)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”.则海岛的高AB=

( ).

2.似曾相识

本问题其实是初中所学知识,苏教版初中数学教材九年级下册数学活动：测量建筑物的高度.

测量底部不可直接到达的物体的高度问题,对于初中生来说不是个难问题,可按下面的步骤进行(如图所示)：

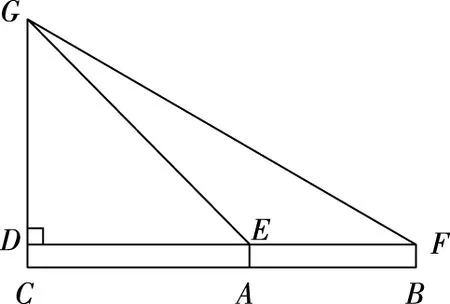
(1)在点B处安置测角仪,测得∠GFD=α.

(2)在点B与物体CG之间的A处安置测角仪(A，B与C都在同一条直线上),此时测得∠GED=β.

(3)测量出测角仪的高度BF=AE=b,以及点A,B之间的距离AB=a.

有了初中知识的铺垫,2021年全国乙卷第9题就不难解决了.

3.真题解答

解：如图，连接FD,并延长FD交AB于M,设∠BFM=α,∠BDM=β,则

4.命题特点

4.1 起点低,但在创新中设关卡

《中国高考评价体系》明确了“一核”“四层”“四翼”,高考的考查要求要注重基础性,能够面向大多数考生,但是也要有区分度.本题以初中数学知识为起点,考查具有基础性,但是处在第9题的位置上,不能过于简单,源于初中课本而高于初中课本,在仰角正切值的转化上设了关卡,产生了区分度.虽易上手,但不易走出来,在初中数学教材中《测量建筑物的高度》的基础上进行创新,贯通了初高中知识的衔接与融合,再次体现了高考试题的创新性原则.

4.2 着力于数学建模核心素养的考查

随着数学核心素养的提出与践行,近年来对学生数学建模的能力越来越重视,同时高考也侧重对数学建模核心素养的考查,体现高考命题的应用性.本题就是数学建模核心素养考查的很好例证,要求学生将现实情境问题抽象成三角形的数学模型,通过求解三角形来解释现实情境问题,从中培养学生用数学的语言表达世界的学科素养.

由此可见,本题符合选拔性的要求,通过数学建模考查学生分析问题、解决问题的能力以及数学阅读的能力,并不是机械地死记硬背,而是以能力立意,重视对数学知识的深刻理解,以及数学思想方法的考查.新教材已经专门设置了“数学建模与数学探究活动”主线,每一章都有一个“数学建模与数学探究活动”的专题,实现了数学建模的课程化,凸显落实数学建模核心素养的重要性.

4.3 渗透数学文化和课程思政

本题以我国魏晋时期刘徽撰写的《海岛算经》为素材进行命题,渗透数学史,传播数学文化,发扬科学精神,学习数学家们的数学成果以及优良的治学品质.高考试题中渗透数学文化是近年来的一大热点,尤其是渗透我国数学家在数学发展中的贡献,有助于增强学生的爱国主义精神,集体荣誉感和民族自豪感,引导学科教学注重课程思政教育,弘扬正能量和核心价值观,以立德树人为根本任务.

5.命题趋势

从近年来高考试题中创新题的高频率出现来看,2022年高考创新题仍然会出现,而且具有以下几点的命题趋势:

(1)素材源于课本而高于课本.高考题选材于课本的频率较高,所以高考复习回归课本是非常有必要的.

(2)设置现实情境问题,立足于数学建模核心素养的考查.就像史宁中教授所说:要教会学生用数学的语言表达世界.

(3)渗透数学文化和课程思政.高考命题的核心是立德树人、服务选才、引导教学.

(4)能力立意,不是简单的生搬硬套,但是要强调通性通法,考查数学思想方法的应用,体现高考试题的综合性.

鉴于以上的命题趋势,自编两道创新题与读者分享:

【自编题1】2020年7月23日12时41分,我国首次火星探测任务“天问一号”探测器发射升空,其任务目标是通过一次发射,实现火星环绕、着陆和巡视探测.2021年3月26日,国家航天局发布两幅由“天问一号”探测器拍摄的南、北半球火星侧身影像.图像中,火星呈“月牙”状,表面纹理清晰.在地球上发射的物体摆脱地球引力束缚,飞离地球所需的最小初速度称为第二宇宙速度.发射“天问一号”探测器摆脱地球引力束缚,去探测火星所需的最小初速度就要达到第二宇宙速度.设从地面垂直向上发射的“天问一号”的质量为m,初速度为v0,若它飞到无穷远处克服地球引力所做的功为W,则第二宇宙速度为

( )

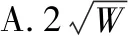
命题意图：本题考查不等式、函数最值等知识，考查函数与方程的思想，考查分析问题、解决问题、实践创新的能力以及数学建模核心素养.试题本身难度并不大,但是在情境问题中抽象出数学模型,解决实际问题,而且打破了高中物理中给出第二宇宙速度的方式,淡化了记忆具体表达形式的思维定式,突出了数学原理本质,这样一来就稍有点难度了.同时,以我国“天问一号”探测器为背景,既突出了数学与自然科学的联系,体现数学文化,又可以激发学生的爱国主义精神.

预设难度：0.7

【自编题2】如图是某省2021年10月17日至2021年10月30日第二次爆发新冠肺炎疫情累计确诊病例人数y的趋势图.

(1)分别利用这两个模型预测2021年11月4日的累计确诊病例人数(保留整数)；

(2)你认为用哪个模型的拟合效果更好一些？并说明理由.

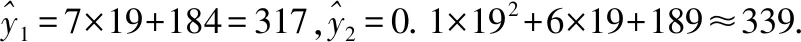
故模型②的拟合效果更好一些.

命题意图:本题考查回归分析等知识,渗透时代背景,考查应用意识、创新意识,落实数据分析、数学建模、数学运算等数学核心素养.本题数学建模中多了一个模型评价环节,与后续课程接轨.

预设难度：0.7

6.一点思考

6.1 高三二轮复习应设计创新题专题复习

相当一部分学生遇到创新题通常都有恐惧心理,尤其是以现实情境为背景,往往连题都读不懂,加上数学建模的能力较弱,以致产生放弃的心理.因此,攻克创新题,提升数学建模的能力不能停留在嘴上,应该落实在二轮备考专题复习的实践中,设计创新题专题复习计划和教学设计,引导学生在系统的训练中认识创新题、走进创新题,降低恐惧心理,锻炼数学阅读能力,提升分析问题和解决问题的能力,掌握数学建模的一般步骤,落实数学建模核心素养.

6.2 高三二轮复习应采用大单元整体复习教学设计

一道好的考题往往是若干个核心概念的交汇,注重知识的联系性,教师要引导学生打破现有章节的限制,将相关的知识整合在一起,采用单元整体教学设计,重新建构认知结构,有助于从整体上厘清主线与核心概念,强化通性通法,做到一通百通,触类旁通,提升知识迁移的能力.

6.3 高三复习更需要课程思政