重视“以退为进”策略渗透 升华学生数学核心素养——以高三“数列”复习为例

甘肃 焦永垚

“以退为进”是高中阶段一种重要的解题策略，在解决复杂问题A时，教师可以先引导学生“退”到他们有所认识且较为简单的问题B中，让学生真正认清问题的本质，从而自然而然地解决了复杂问题A，这一过程可以简单地用如图所示的流程图表示：

高三数学复习教学要重视以退为进解题策略的渗透，这对学生而言，不仅是解题方法的培养，而且是创新能力的培养，可以有效地升华学生数学核心素养.

1.重视“模型思想”渗透，在“以退为进”中“退”出境界，解的完美

“模型思想”是数学核心素养的重要内涵，“模型思想”不仅能为我们快速探明解题方向，而且还能有效简化解题途径.例如，我们经常利用放缩法证明数列求和型不等式，这类问题的难点是学生不知道往哪个方向放缩或怎样放缩，但有一个目标是统一的，就是将不可求和的数列问题化为可求和的数列问题，这就需要我们合理地“退”，将问题“退”为一个学生所熟悉的数列模型，如等差数列模型、等比数列模型或能够裂项相消求和的数列模型等等，因此学生在熟练掌握一些数列求和模型的基础上，还要学会怎么“退”，往哪个方向“退”，只有掌握了这些方法才能退出境界，解的完美.

【案例1】已知数列{an}满足a1=1，an+1=3an+1.

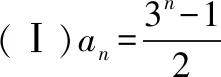
视角一：“退”为一个等比数列

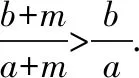
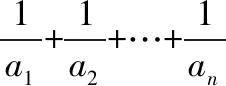
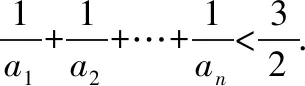
视角二：“退”为一个能“裂项相消”求和的数列

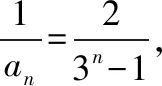
当n≥2时，

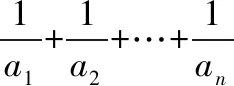
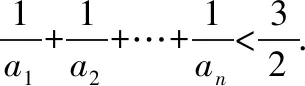
视角三：把求和问题“退”为比较两个数列对应项的大小的问题

策略1：执果索因，逆推探源

策略2：逆用累加法

2.理解问题的本质和知识间的内在联系，“退”出创新，“退”出精彩

常数列是在所有数列中属于最平常最简单的一类，对于一些求数列的通项公式或数列求和的问题，只要学生能够理解问题的本质及数列知识间的内在联系，能将所求的数列的通项或前n项和“退”为一个常数列，这样不仅使问题变得简单，而且还“退”出了创新，“退”出了精彩.

【案例2】(2020·全国卷Ⅲ理·17)设数列{an}满足a1=3，an+1=3an-4n.

(1)计算a2,a3，猜想{an}的通项公式并加以证明；

(2)求数列{2nan}的前n项和Sn.

分析：(1)易得a2=5，a3=7，由此猜想an=2n+1，下面分析如何证明：

对于第(2)问，我们也可以尝试将Sn“退”为一个常数列.由⑴可得2nan=(2n+1)·2n，设bn=(2n+1)·2n，则

bn+1-bn=(2n+3)·2n+1-(2n+1)·2n

=(2n+5)·2n

=(2n+1)·2n+2n+2

=bn+2n+2，

即bn=bn+1-bn-2n+2，这样我们就找到了一个bn+1和bn的关系式，因为当n≥2时，bn=Sn-Sn-1，如果忽略bn=bn+1-bn-2n+2中的“-2n+2”，则有Sn-bn+1=Sn-1-bn(即数列{Sn-bn+1}为一个常数列)，而“2n+2”为一个以2为底的指数式，我们将其“分摊”给等式Sn-bn+1=Sn-1-bn的两边，这个“分摊”也可以由待定系数法实现：

设Sn-bn+1+λ·2n+1=Sn-1-bn+λ·2n，则bn=Sn-Sn-1=bn+1-bn-λ·2n，与bn=bn+1-bn-2n+2比较可得λ·2n=2n+2，解得λ=4，于是Sn-bn+1+4·2n+1=Sn-1-bn+4·2n，且S1-b2+4×22=2，所以数列{Sn-bn+1+4·2n+1}是各项为2的常数列，则Sn-bn+1+4·2n+1=2，所以Sn=bn+1-4·2n+1+2=2+(2n-1)2n+1.

该题的两问分别为求数列的通项公式和前n项和，第(1)问也可以先猜出通项公式后再用数学归纳法证明，第(2)问也可用学生熟知的“错位相减法”解决，但上述解法中我们都将所求数列“退”为一个常数列再解决，思维具有创新性，解答完给人一种“酣畅淋漓”的感觉，既如鱼得水，又势如破竹，而且这样的解题也有利于培养学生良好的创新思维与发散思维，有利于提升学生的数学核心素养.而利用数学归纳法和错位相减法解决问题，结论虽然正确，但仅表现为具体解题的一招一式，思维仍然停留在感性认识和简单应用的阶段，尤其对于一些非常复杂的问题，两种思维的差距就会明显拉大.

3.“退”到最原始的地方，才能看清问题的真谛

著名数学家华罗庚说过:“善于退，足够地退，退到最原始而不失重要的地方，是学好数学的一个诀窍”.对于一些复杂的问题，当从正面直接去解决有困难时，我们可以从最简单的特殊情况入手，一步一步进行尝试，抽丝剥茧，再坚持一步兴许就会豁然开朗，柳暗花明.有些复杂问题只有退到最原始的地方，才能看清问题的真谛.

【案例3】(2020·新高考Ⅰ卷(仅供山东使用)·18)已知公比大于1的等比数列{an}满足a2+a4=20，a3=8.

(1)求{an}的通项公式；

(2)记bm为{an}在区间(0,m](m∈N*)中的项的个数，求数列{bm}的前100项和S100.

分析：第(1)问比较简单，易得an=2n，下面来分析第(2)问.

该题很多学生的感受是“看不懂”，我们需要把学生引“退”到最原始能看懂的地方：

由于数列{an}为2,4,8,16,32,64,128,…，所以当m=1时，区间为(0,1]，显然此区间中没有{an}的项，即b1=0.这一步就是那个“最原始而不失重要的地方”，把这一步认清了，看透了，问题的真谛也就显现出来了，再前进，思维就顺畅了：

当2≤m≤3时，区间为(0,2]，(0,3]，b2=b3=1；

当4≤m≤7时，区间为(0,4]，(0,5]，(0,6]，(0,7]，b4=b5=b6=b7=2；

当8≤m≤15时，区间为(0,8]，(0,9]，…，(0,15]，b8=b9=…=b15=3；

当16≤m≤31时，区间为(0,16]，(0,17]，…，(0,31]，b16=b17=…=b31=4；

当32≤m≤63时，区间为(0,32]，(0,33]，…，(0,63]，b32=b33=…=b63=5；

当64≤m≤100时，区间为(0,64]，(0,65]，…，(0,100]，b64=b65=…=b100=6；

所以S100=b1+(b2+b3)+(b4+b5+b6+b7)+(b8+b9+…+b15)+(b16+b17+…+b31)+(b32+b33+…+b63)+(b64+b65+…+b100)=0+1×2+2×22+3×23+4×24+5×25+6×(100-63)=480.

事实上，该题与高中所学知识没有多少联系，就是纯粹考查学生分析问题和解决问题的能力，像这样的题目，教师一定要让学生亲自动手体验这一完整的解题过程：

只有这样，才能锻炼学生的思维品质，才能使学生的核心素养品质得以升华.这样的以退为进，就是先足够地退到最容易看懂的地方，把最原始最基本的问题认清了，看透了，然后再一步步前进，直至认清整个问题的“庐山”真面目.正因为有了前面的“退”，才能更好地“进”.事实上，此题还可以进一步引导学生探究问题的一般情况：

当2k≤m≤2k+1-1(k∈N*)时，区间为(0,2k]，(0,2k+1]，…，(0,2k+1-1]，b2k=b2k+1=…=b2k+1-1=k，共有2k+1-1-2k+1=2k个k.至于求和，只需利用学生熟悉的错位相减法就可以解决，本文不再赘述.对于这样的复杂问题，只有退到退无可退，才能看清问题的真谛.