湿热定型机温湿度解耦控制系统

赵世海，李 果

（1.天津工业大学 机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津 300387）

织物在生产过程中由于受到机械、化学等作用产生形变，并不能直接用于染色、印花等后续工序的加工。热定型可以消除在生产过程中产生的强迫高强变形，并同时释放纤维的内部应力[1]。热定型后的织物在尺寸稳定性和机械性能方面均得到显著提高，还能使织物表面起球、表面平整性等性能得到改善。

与干热定型相比，湿热定型后的织物手感丰满、柔软[2]。但是传统的温湿度控制系统将温度和湿度作为2个相互独立的系统进行调节，忽略了两者之间的耦合联系，从而使系统的控制质量下降。李旻[3]将模糊理论运用到温度控制，证明该方法稳定可靠；谭宝成等[4]将模糊PID运用到热定型机温度控制中，降低了在控制过程中的迟滞和超调现象。但上述方法均未考虑到在实际应用中来自其他系统的耦合、干扰。

针对湿热定型机这种具有强耦合、大迟滞的温湿度控制系统，本文提出一种基于模糊控制的前馈解耦控制方案。先利用阶跃响应法找到传递函数，并根据传递函数设计出解耦系统，再将模糊控制融入到设计好的解耦系统当中，以达到解耦目的，同时降低在控制过程中的迟滞现象[5]。

1 热定型机温湿度系统建模

热定型机由进布架、操控台、针铗链、燃烧室、烘房、落布架几个部分构成。布料首先放入进布架上，由辊轴输送到针铗链上，被拉幅之后送进烘房，烘房内部结构如图1所示。烘房内对温度调节过程如下：空气在燃烧室被加热后，热风经由鼓风机吹风口吹向胚布，最后与烘房的热蒸汽混合。显然当烘房温度增加时，湿度会随着温度提升而降低；当对湿度进行调节时，饱和水蒸气会通过辊轴内的加湿设备进入烘房内部，温度也会随湿度的增加而降低，即在热定型机内部温、湿度存在较强的耦合关系。为了解除存在于温度、湿度之间的耦合效应，建立烘房内部的合理的数学模型至关重要。

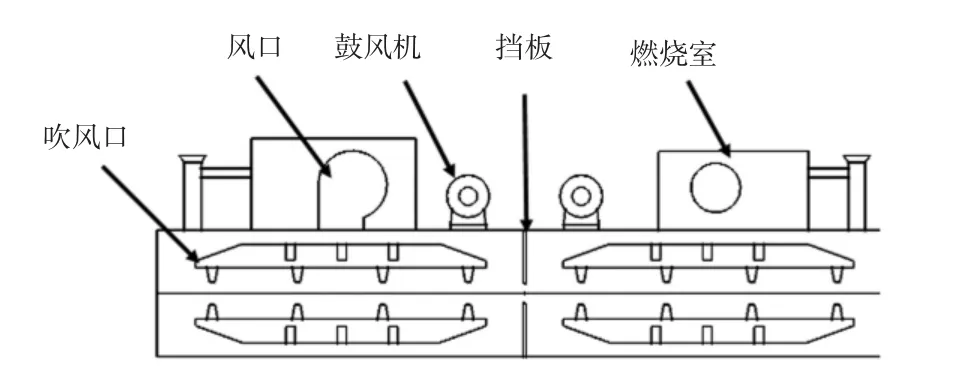
图1 烘房结构示意图Fig.1 Schematic diagram of drying room structure

温湿度系统具有强耦合和非线性特性，烘房内的温度受风道出风口温度、烘房内部体积、初始温度等一些因素影响，在不考虑外界干扰下，根据能量守恒定律[6]：

式中：ρ为空气密度；CP为空气定压比热容；V为烘房内部体积；f为空气流量；Ts为出风口温度；Th为回风口温度。

将模型两边进行拉式变换，得到烘房内温度控制系统为一阶传递函数[7]：

温度控制系统为非线性、大迟滞控制系统，考虑滞后环节影响，串联滞后环节后得到G1（s），传递函数为：

式中：K1为温度控制系统的增益系数；τ、T分别为温度控制系统的迟滞时间和时间常数；s为复变量。

使用阶跃响应法[8]确定加热器-温度的数学模型。实验时箱内温度为50℃，关闭湿度控制器的同时给温度控制器一个扰动信号，记录温度的变化曲线直至稳定，阶跃响应曲线如图2所示。

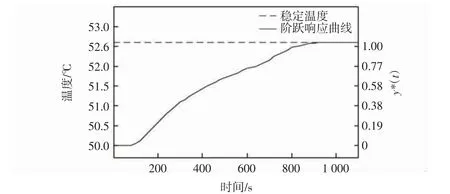
图2 加热器-温度阶跃响应图Fig.2 Diagram of heater-temperature step response

由图2可以得到：

式中：K为比例增量；Y（∞）为系统稳定后温度；Y（t0）为初始温度；Δu=0.5为加热功率干扰量。y*（t）为y（t）的无纲量，y*（t）与公式（3）中的时间常数T、纯迟滞τ满足如下关系[9]，选取2个不同坐标下t1、t2建立如下方程组：

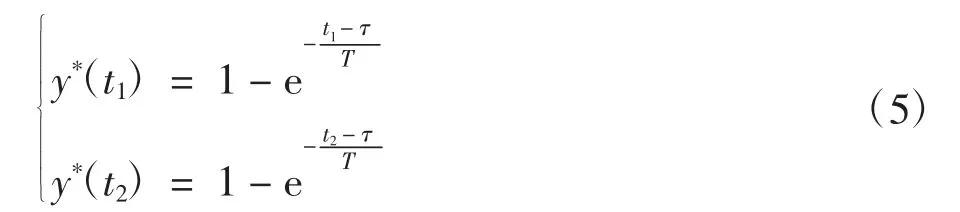
在图2中，当y*（t1）=0.39时，t1=280 s，y（t1）=51.04；y*（t2）=0.63时，t2=460 s，y（t2）=51.6。将参数带入式（5）解得T=360，τ=100，。将求解结果带入式（3）既得出加热器-温度系统G11的数学模型为：

使用上述方法可求得G12、G21、G22的数学模型为：

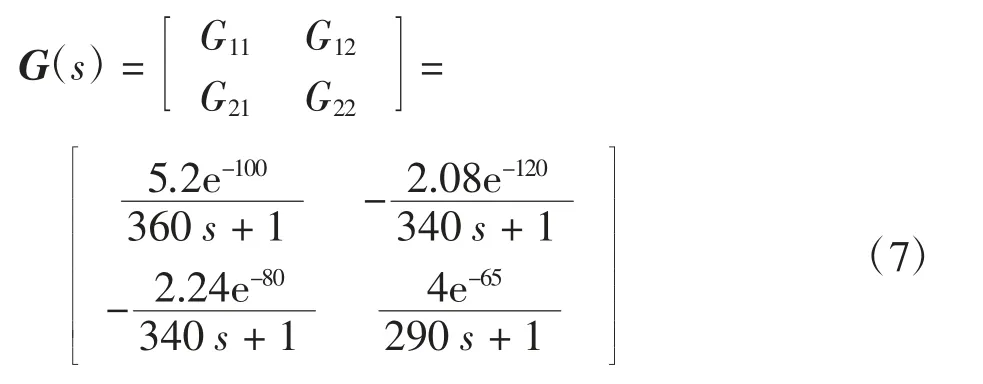
式中：G11为加热器对温度传递函数；G21为加热器对湿度传递函数；G12为加湿器对温度传递函数；G22为加湿器对湿度传递函数。

2 前馈补偿解耦方案

当产品在烘房进行加工时，温度和湿度都是影响产品质量的重要因素。但在烘房内部，温、湿度并不是独立的变量[10]，单一地调节某一方，都会引起另一方的变化。温度、湿度之间的耦合关系如图3所示。

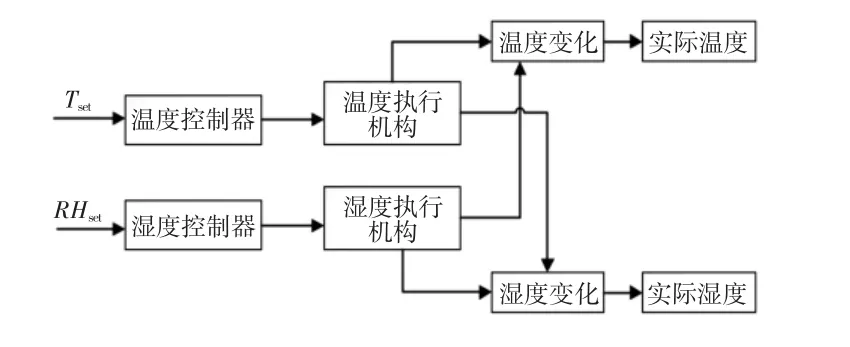
图3 温度湿度耦合关系图Fig.3 Coupling diagram of temperature and humidity

由温湿度耦合关系得出热定型机控制与输出之间的传递矩阵：

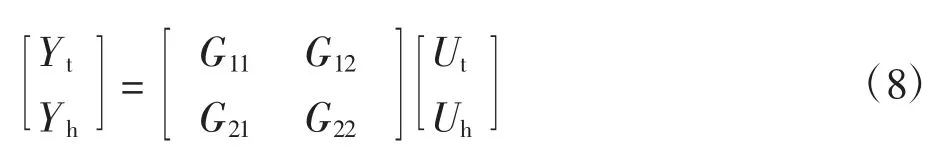
式中：Yt、Yh为烘房内部的温度和湿度；Ut为温度控制器输出；Uh为湿度控制器输出。温度和湿度的输出结果均被Ut、Uh共同控制[11]。

针对温湿度系统耦合控制不理想的问题，采取前馈解耦的方式。前馈解耦是根据控制不变性原理来设计解耦控制器的，以矫正方式使温度和湿度在调整过程中稳定在设定值，达到解耦目的[12]。解耦控制原理如图4所示。

图4 温度湿度解耦控制原理图Fig.4 Schematic diagram of temperature and humidity decoupling control

式中：Tset为设定温度；RHset为设定湿度；Ut为温度控制器输出；Uh为湿度控制器输出；F21为温度-湿度解耦传递函数；F12为湿度-温度解耦传递函数；

在工作过程中湿度的增加会影响温度的变化，反之亦然。通过测量干扰的大小和方向[13]，增加前馈补偿模型以抵消干扰对被控量的影响。F12、F21为前馈补偿信号，传递矩阵为：

在解除耦合后，温度、湿度不再相互影响。此时可将式（9）传递模型看作对角矩阵，当控制矩阵变为对角矩阵后，Yt仅被Ut控制，Yh也仅被Uh控制，输入输出关系可由式（10）来表示：

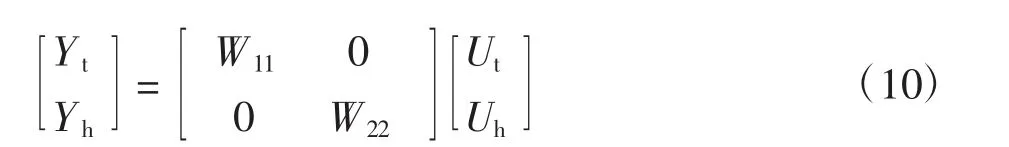
将式（10）代入式（9）中求出解耦传递函数F21、F12和等效传递函数中的W11、W22：

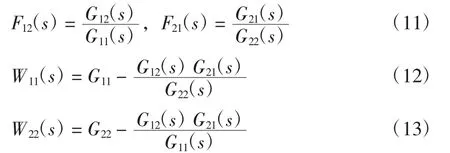
在文中设计的温湿度控制解耦环节中，图4控制器C1（s）、C2（s）采用模糊控制的方式，可有效降低控制过程中的迟滞[14]。在加入补偿矫正后，温度、湿度控制系统的耦合效应消除，经过解耦后的控制系统等效图如图5所示。

图5 温湿度解耦等效图Fig.5 Equivalent diagram of temperature and humidity decoupling

3 模糊控制模块设计

PID控制具有结构简单、工作可靠、易于调整等优点，被广泛运用在工业生产中。但当系统中含有复杂变量或者没有具体数学模型时，传统的PID控制很难获得理想的控制效果[15]。模糊PID控制器会将实际值与期望值的偏差和偏差变化率2个参数输入到模糊控制器中[16]，在经过模糊化、模糊推理和解模糊过程后得到ΔKP、ΔKI和ΔKD3个修正参数，并将3个参数输送给PID控制器得到新的KP、KI、KD。模糊PID控制器充分利用了人工调节实践经验，在控制过程中对PID参数进行调整，与传统PID控制相比反应更加迅速，在遇到干扰时拥有更好的鲁棒性[17]。模糊控制器结构如图6所示。模糊控制器设计过程主要包括：输入量e、ec模糊化；模糊推理；反模糊化。

图6 模糊PID系统结构Fig.6 Structure of fuzzy PID system

3.1 e、ec模糊化

模糊化是将输入量e、ec由精确值变为模糊语言变量值的过程。将模糊语言变量子集划分为“NB”（负大）、“NM”（负中）、“NS”（负小）、“ZO”（零）、“PS”（正小）、“PM”（正中）、“PB”（正大）7个变量等级。根据隶属度函数确定隶属度[18]，隶属度函数这里采用高斯隶属函数，如图7所示。

图7 输入变量的隶属度函数Fig.7 Membership function of input variables

3.2 模糊推理

决策推理是模糊控制的核心，输入量依据模糊规则得到相应输出变量ΔKP、ΔKI和ΔKD。按照热定型机管控人员的日常经验，归纳整理成模糊规则库，使用if A and B then C语句进行模糊规则的设计[19]。每1个输入量均含有7个语言变量值，因此，模糊规则的个数共为49个。

3.3 反模糊化

反模糊化是指将3个输出变量由模糊语言变为3个具体的数值[20]，去对应PID控制器的3个参数ΔKP、ΔKI和ΔKD。输出变量的语言变量值为“NB”（负大）、“NM”（负中）、“NS”（负小）、“ZO”（零）、“PS”（正小）、“PM”（正中）、“PB”（正大），隶属度函数同样为高斯函数，如图8所示。

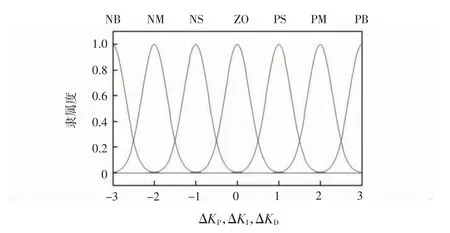
图8 输出变量的隶属度函数Fig.8 Membership function of output variables

4 仿真实验

传统的温、湿度控制系统实际将温度、湿度看作2个相互独立无关联的控制变量，但在实际控制过程中温、湿度耦合作用明显。在加入模糊和解耦模块后以Matlab作为仿真平台，分别对耦合系统以及解耦的系统进行仿真模拟，对解耦效果进行验证。

4.1 温、湿度控制效果仿真

设置烘房温度初值为20℃，相对空气湿度为30%，湿热定型稳态下工作温度为130℃，当采用饱和蒸汽时效果与水浴法接近，定型效果较差，本文采用工作时相对湿度为80%。温、湿度2个参数的采样周期均设置为10 s一次，仿真时间为3 500 s。仿真结果如图9、图10所示。

图9 耦合系统与模糊解耦系统的温度仿真结果Fig.9 Simulation results of temperature in coupled system and fuzzy decoupling system

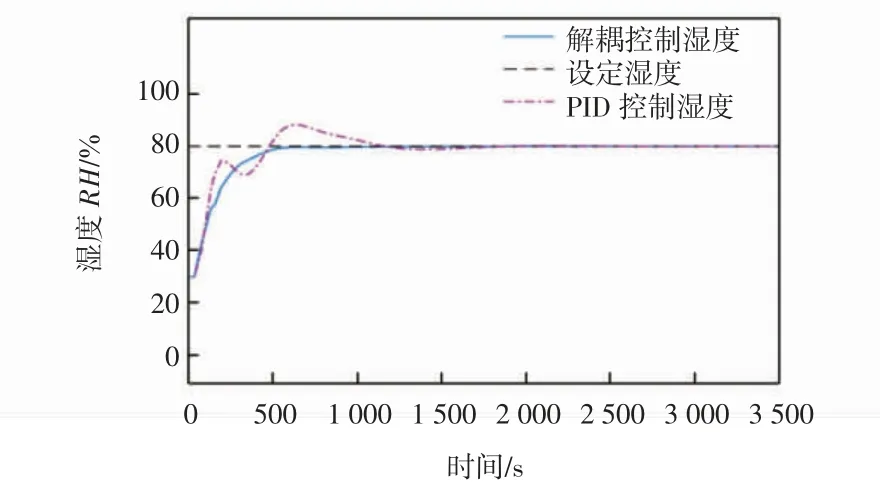
图10 耦合系统与模糊解耦系统的湿度仿真结果Fig.10 Simulation results of humidity in coupling system and fuzzy decoupling system

由图9、图10曲线可知：当使用传统PID控制器对温湿度进行控制时，温度超调量达到23%，调节时间约为1 700 s；湿度的超调量为10%，调节时间为1 600 s左右。温、湿度超调量过大在生产过程中是不被允许的，这会造成产品质量的不稳定，甚至会破坏生产设备。在使用模糊解耦控制时，温湿度系统的超调量明显下降，且震荡平缓。温度系统的调节时间由原来的1 700 s降低到1 100 s，且超调量几乎为0；湿度系统的调节时间由原来的1 600 s降低至700 s，且超调量为0。解耦后的系统超调量小、稳态精度高，具有较好的动态响应特性和静态特性，满足系统的控制要求。

4.2 稳定性仿真

为验证在加入解耦模块后温湿度控制系统的稳定性和抗干扰的能力，在2 700 s时分别给温度回路和湿度回路一个干扰信号，来模拟实际工况下的环境干扰和人工干预，仿真结果如图11、图12所示。

图11 耦合系统与模糊解耦系统加入干扰后的温度仿真结果Fig.11 Temperature simulation results of coupled system and fuzzy decoupling system after adding interference

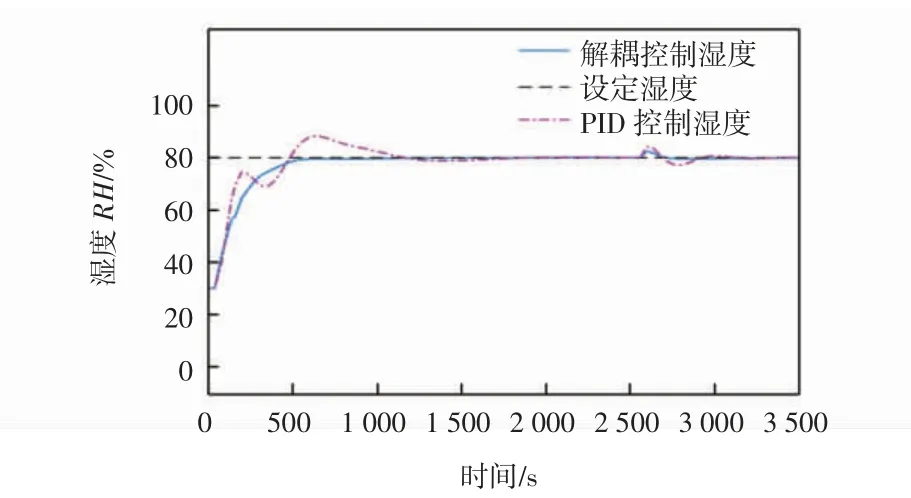
图12 耦合系统与模糊解耦系统加入干扰后的湿度仿真结果Fig.12 Humidity simulation results of coupled system and fuzzy decoupling system after adding interference

由图11、图12曲线可知：当控制系统受到外界条件干扰或人为干预后，在使用传统PID控制器控制时，温度、湿度系统均震荡明显，且收敛缓慢；而在使用模糊解耦控制时，温度、湿度受外界扰动的影响变小，且以更短的时间达到稳定值，鲁棒性有了很大提升，说明模糊解耦控制器具有良好的扰动补偿和抗干扰能力。

4.3 解耦效果仿真

对系统解耦效果进行验证，在2 100 s时分别调整解耦系统和无解耦的工作温度，将工作温度由130℃调整至150℃，观测温度的变化和湿度是否存在耦合效应，仿真结果如图13、图14所示。

由图13、图14可知：在2 100 s时温度控制器得到控制信号，将系统工作温度由130℃调整至150℃。使用模糊解耦控制的温度能够迅速到达稳态，并且在解耦后湿度无明显变化。在无解耦控制时，由于温度的调节，湿度发生明显的波动，在2 250 s时湿度的数值降低至72%，然后在2 500 s后重新到达相对湿度80%，湿度的波动量为10%。

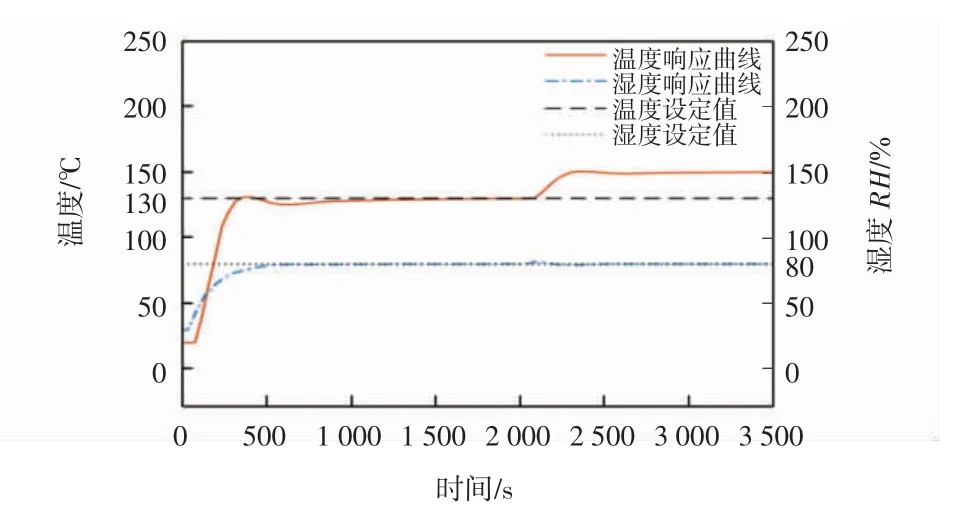
图13 温度调节后解耦系统响应曲线Fig.13 Response curve of decoupling system after temperature regulation

在2 100 s时对工作湿度进行调整，相对湿度由80%调节至90%，仿真结果如图15、图16所示。

由图15、图16可知：在2 100 s时湿度控制器接收调节信号，相对湿度由80%调节至90%，观测温度和湿度的变化。在使用模糊解耦控制时，湿度改变后温度几乎无变化；在无解偶控制时，由于湿度的调节，温度在2 250 s时由130℃降低至120℃，并且在2 400 s时重新到达稳态，温度的波动量为7%。

图16 湿度调节后无解耦系统的响应曲线Fig.16 Response curve of undecoupling system after humidity regulation

5 结论

本文提出了基于模糊控制的解耦方案，使用Matlab对解耦系统和传统PID系统仿真，得出如下结论：

（1）超调量方面，在使用PID控制时温度超调量为23%，湿度超调量为10%；在加入模糊和解耦模块后超调量几乎为0。

（2）调节时间方面，使用PID控制时，温度到达稳定时间为1 700 s，湿度到达稳定时间为1 600 s；当加入模糊和解耦模块后，温度到达稳态时间降低至1 100 s，湿度到达稳态时间降低至700 s。

（3）稳定性方面，在加入干扰时，使用传统PID控制的温湿度震荡更加明显，收敛缓慢；而使用模糊解耦控制时，震荡相对平缓，收敛时间减小。

（4）温、湿度耦合方面，在使用模糊解耦控制时，分别对温度、湿度进行调节后，几乎对系统没有耦合影响；当使用无解耦控制时，温湿度的耦合效应明显。

综上所述，对于温、湿度这种具有强耦合、大迟滞的控制系统，模糊PID前馈解耦控制比传统PID控制反应更灵敏、迅速，在加入干扰时拥有更好的鲁棒性，并且在温、湿度的控制过程中，达到了一定的解耦效果。