挖掘特征 深思致远——对一道空间截面问题的拓展探究

广州市执信中学(510080) 朱清波

数学的学习过程离不开解题,学生在解决问题的过程中能巩固知识和学会思考,高考备考中,若教师只注重解题的熟练度,将教学的高效表现片面理解为“短时间内教授最多知识”无疑是短视和功利的,忽略知识生成规律的教学对学生思维能力上的提升也相当有限.波利亚在其著作《怎样解题》中曾提到:“问题真正获得解决的评判标准应是我们对原问题的理解比刚开始时更完整和准确”.因此,教师在教学过程中应有针对性地选择具有启发性的问题引领学生剖析思路、探究解法、反思过程并发现规律,突出体现解题的思维过程与涉及到的数学思想方法.让学生在原有认知的基础上又有新的收获,这是课堂复习效率评价的最重要指标.以下是笔者在高三备考过程中的一个解题拓展片段,以此来说明上述观点.

一、问题呈现,解法探究

题目1如图1 所示的木质正四棱锥模型P - ABCD,过点A作一个平面分别交PB,PC,PD于点E,F,G, 若的值为____.

图1

试题分析本题考查的是空间四点共面问题,考点清晰但缺乏问题解决和转化的数学工具,对学生的几何直观和逻辑推理能力提出了较高的要求,难度较大.

解法1利用平面延展的相关性质, 直接找到该平面和直线PD的交点G,将空间问题转化为平面几何问题.

如图2,延展平面AEF,设EF与CB相交于M,MA与CD相交于T,TF与PD相交于G, 如图3, 在ΔPBC中,作BN//PC,交MF于N;在ΔPDC中,作DS//PC,交TF于S,利用平几知识有

图2

图3

评析解法1 需要较强的空间想象能力,将空间问题平面化,对学生的平面几何相关性质的应用提出了较高的要求,故思路容易想到但在解题中会遇到转化困难,不易完整解决.

解法2利用向量,直接从代数运算方向处理空间四点共面.如图1,因为G在PD上,设又A,E,F,G四点共面,设

利用空间向量基底表示的唯一性,对比可知:

评析向量在描述三点共线和四点共面时具有鲜明的特征,解法2 体现了它的工具性作用,相比解法1 而言对学生的空间想象能力要求不高,但对运算能力提出了挑战.

从解答过程来看,当三个不在同一条直线上的点确定一个面后,则第四个交点的位置必然是确定的,那么该点和前三个点的位置会不会有某种关联? 解法1 的过程从形的角度上揭示了四个点之间的联系,这提示我们可尝试利用解法2的思路,从数的方向去寻找隐藏在这个具体情境中的一般规律.

二、纵向延申,深入拓展

从考查特征来看,本题在研究空间中某个截面的几个交点位置的规律,类比到平面上应对应着某条线与两条边的交点规律,而在教材平面向量模块章节中,有如下与之类似的习题:

题目2(新课标人教版必修2 第39 页练习3)如图4,在ΔABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,设AM=mAB,AN=nAC,求的值.

图4

解析由

又M,O,N三点共线,则

重观题目1,若在某平面截四条直线PA,PB,PC,PD的四个截点中任选两个截点进行考查,就转化成平面上的相关问题(即题目2),现选择相对的两个截点为一组(共两组),利用题目2 的解决思路尝试探究这两组截点分布的规律.

探究如图5, 在正四棱锥P - ABCD中, 平面α与四条侧棱PA,PB,PC,PD分别交于点M,N,S,T, 记试探究u1,u2,u3,u4之间的等量关系.

图5

解析如图6,连结AC与BD,设交点为O,连结MS与NT, 设交点为H, 因为P,H,O均为面PAC和面PBD的公共点, 则P,H,O三点共线.在ΔPAC中, 如图7,记由则化简得由O是AC中点,则解得则

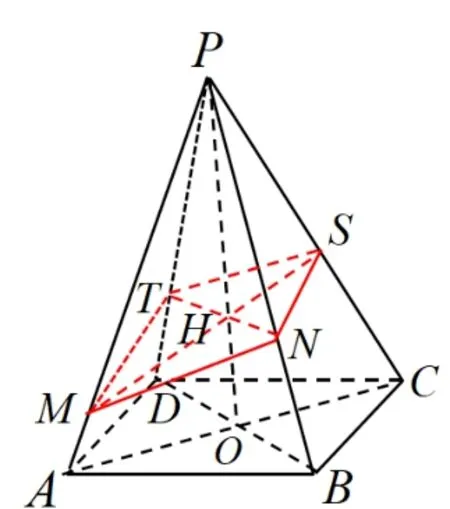
图6

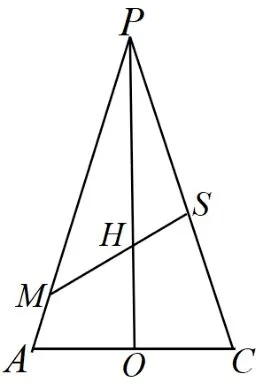
图7

同理在ΔPDB中, 如图8, 有对比可知,此即为u1,u2,u3,u4之间的等量关系.

图8

值得反思的是,从探究过程来看,四棱锥P -ABCD无无需满足正四棱锥这样的“严格条件”,底面ABCD为平行四边形时结论就成立;另外从推导过程分析,四个截点位置也无需在底面的同侧,即截面与侧棱的四个交点分布在底面ABCD的异侧时,结论也成立,故归纳后可得到如下性质:

结论1如图9,在四棱锥P -ABCD中,底面ABCD为平行四边形, 若平面α与四条侧棱PA,PB,PC,PD所在直线分别交于点M,N,S,T, 记,则

图9

利用结论1 进一步思考, 如果截面只跟其中三条侧棱(或延长线)相交,会有什么结论? 经过探究可得到如下性质:

结论2如图10,若截面α与底面为平行四边形的四棱锥P -ABCD的三条侧棱PA,PB,PC所在直线分别交于点M,N,S三点,记则PD//α的充要条件为

图10

证明先证明充分性,用反证法,若PD与α不平行,则PD与α相交,记PD与α交点为T,设利用结论1 中结合对比可知矛盾, 故假设不成立, 即原结论成立, 于是有PD//α.

图11

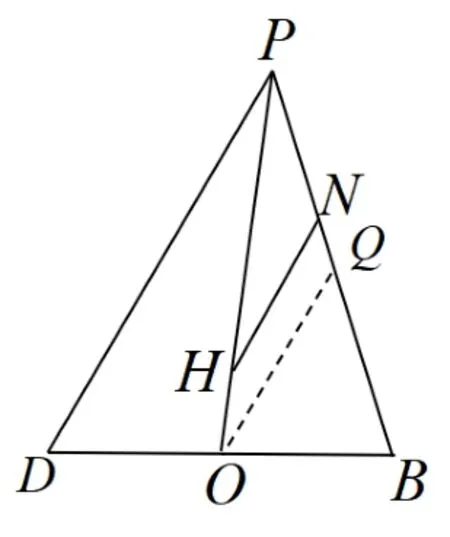
图12

综上,则原命题成立.

结论2 可为空间中一类线面平面的存在性问题提供一个新的思路.

题目3(2018年高考全国Ⅲ卷文科第19 题节选)如图13, 矩形ABCD所在平面与半圆弧所在平面垂直,M是上异于C,D的动点.(2)在线段AM上是否存在点P,使得MC//平面PBD,说明理由.

图13

解析记因为MC//平面PBD,利用结论2,令解得即P为AM中点时符合题意.

同时,利用探究活动中,也能发现以原四棱锥的顶点为顶点、四个截点构成的四边形为底面形成的新四棱锥,其体积与原四棱锥的体积应存在某种关联,经探究可得到如下结论:

结论3如图14, 四棱锥P - ABCD的底面ABCD是平行四边形, 若平面α与四条侧棱PA,PB,PC,PD所在直线分别交于点M,N,S,T, 记四棱锥P - ABCD的体积为VP-ABCD,四棱锥P -MNST的体积为VP-MNST,则

图14

证明如图15,记三棱锥P-MNT的体积为VP-MNT,其余三棱锥体积表示法类似.由

图15

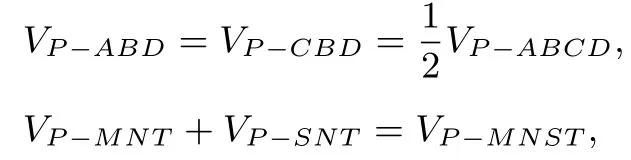
则

故

也成立.

解题不仅仅是会做题和做对题,重视解题反思,指导学生对问题进行深入的探究,能更好地帮助其看清问题的本质,从而达到“做一题会一类”的效果.当然能否及时捕捉到一个好的问题也依赖教师自身的学科素养.如果学生在日常的教学活动中不断地学习到这些深度思考和类比迁移,在后续的学习过程中也必然能自发产生类似的深层次疑问并主动探究交流来解决相关困惑,从而有效提升自身学科核心素养.