基于熵权TOPSIS法的高考数学试卷评价模型的建立及应用*

云南省昆明市云南师范大学(650500) 杨聪聪 闫芳

1 问题提出

2020年1月,教育部考试中心发布了《中国高考评价体系》、《中国高考评价体系说明》,指出中国高考评价包括高考的核心功能、考查内容和考查要求.《中国高考评价体系》是高考命题、评价与改革的理论基础和实践指南[1].高考数学必须依托于高考评价体系,凸显具有数学特色的考试与选拔要求.可是什么样的试题才是符合这个要求的呢? 怎样客观、科学、合理、全面地分析和评价高考数学试题? 这是目前广泛关注的问题.以往对于高考数学试题的分析多从难度出发去衡量一份试题的难度系数[2-3].或者是从高中数学核心素养的角度评价高考数学试题[4-5],其评价都具有一定的片面性.但是高考评价体系进一步将核心素养深化,它是一体两面的综合体系,以“四层”为考查内容,评价考生素质内涵;以“四翼”为考查要求,评价学生素质达成度[1].综上可得,以高考评价体系作为高考数学试卷评价的理论依据更为全面、科学.基于以上的思考,本文以高考评价体系为研究前提和依据,结合数学学科特点,架构分析框架,制定评价指标,并以此为分析工具,采用定量研究的方法分析2021年高考数学共9 套(上海卷除外)试题,并在此基础上采用熵权法求得各个评价指标的权重,构建高考数学试题评价模型,最后利用TOPSIS 法对以上9 套试卷进行综合评价排序.

2 研究设计

2.1 构建高考数学试卷评价框架

本文参考了《中国高考评价体系》[1]和任子朝、赵轩学者的相关研究[6],结合数学学科特点,绘制了高考数学评价体系关系图,如图1 所示:

图1

2.1.1 “四层”指标的具体分析

由图1 知,高考数学科的功能定位为: 发挥数学学科特点、以测试数学综合能力、发展数学核心素养为目标[6],其核心功能的实现依赖于“四层”、“四翼”、“情境”的考查.另外从具体分类来看,“四翼”和“情境”是同一指标的不同层次,具有明显的层次性,对学生的能力要求呈递增的趋势,而四层的分类是基于不同的四个指标,为了更好地体现“四层”的指标层次性以及实现后续的定量研究,本文参考普通高中数学课程标准(2017年版2020年修订)[7]和段志贵与黄云鹤学者基于高考评价体系的试卷分析[8],将“四层”指标进一步细化,如图2 所示:

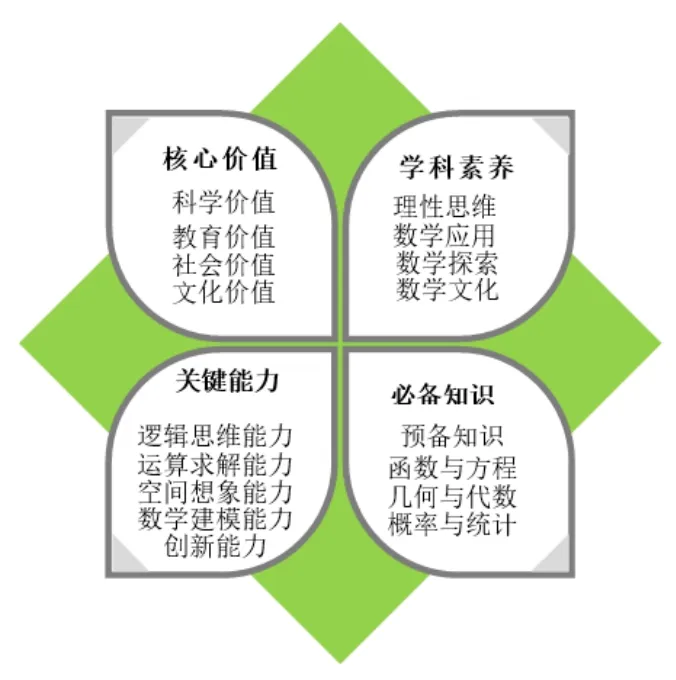
图2

由图2 可知“四层”中的前三层指标之间具有一定的相关性,但是必备知识分为四个主题,且各个主题间相互独立,所以本文首先对这部分展开探究.在此统计了2021年(除上海卷外)9 套高考数学试卷在必备知识的考查分值比例,如表1所示:

表1 各试卷必备知识的分值考查比例表

由表1可知各试卷在各主题下的分值占比非常接近,为了更精确地检验这些占比之间的一致性,在此进行了Kendall W 协调系数分析,结果如表2:

表2 Kendall W 协调系数分析表

从表2可以看出: Kendall 协调系数检验呈现出显著性(p= 0.000＜0.05),意味着9 份试卷在四个主题的分值占比具有关联性, 即说明评价具有一致性.同时Kendall 协调系数为0.990,大于0.8,说明评价一致性程度很强,差异性较小.因此在本研究中没有将“必备知识”纳入对比评价指标.

2.1.2 高考数学试卷评价框架

在去除“必备知识”指标后, 本文以“四层”中的核心价值、学科素养、关键能力以及考查要求、考查载体,共同构成高考数学试题评价模型,具体含义及权重如表3[7].

由表3可知: 在该评价框架中,一级指标有5 个,分别是核心价值、学科素养、关键能力、考查要求、考查载体.

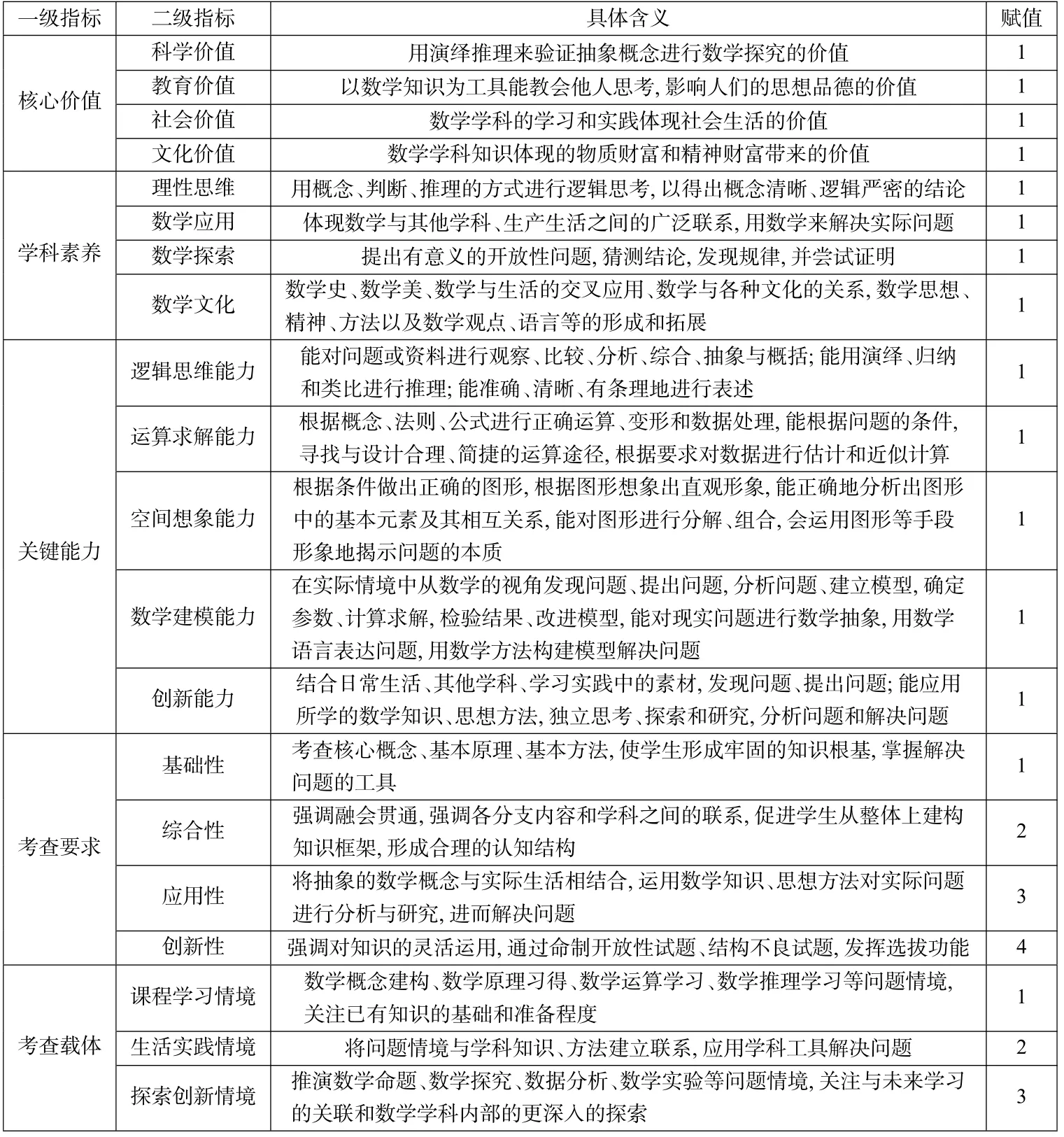
表3 评价指标含义-赋值表

二级指标细分为20 个,由于前13 个指标相互独立,不具有明显的层次性,所以权重都赋值为1,而后7 个指标对学生能力要求具有明显的层次性,根据要求能力的强弱,赋予了不同的权重.

2.2 高考数学试题评价指标的编码方法

为了使本研究更具有代表性,在此选取了2021年高考数学试卷(上海卷除外)共9 套试题为研究对象,对试卷中的每一个题目根据以上指标进行赋值,其中前三个一级指标在同一个题目中可能会考查多个二级指标,所以该题目符合几个二级指标,就给对应的一级指标赋数值为几的权重.

具体赋值方法如下,以2021年全国乙卷(理数)第9 题为例:

例魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图3, 点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高AB=( )

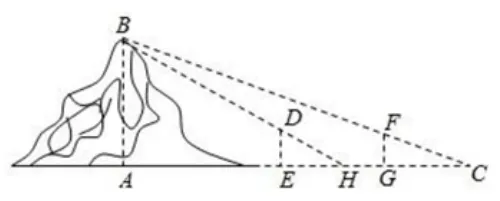
图3

该题以魏晋时期我国数学家刘徽在其著作《海岛算经》中的测量方法为背景,要求考生根据测量过程中的相关条件,推断海岛高度的计算方法.试题在考查考生综合运用知识解决问题能力的同时,也让考生充分感悟到我国古代数学家的聪明才智.其中科学价值、教育价值、社会价值、文化价值都有体现,所以核心价值赋值为4;学生在求解时需要理清各数量间的关系,利用三角函数构建模型,理性思维、数学应用、数学探索、数学文化都有所体现,所以学科素养赋值为4;此外题目的设问较为新颖, 求解过程学生需要正确做出图形,自己构建求解模型,考察到了学生的创新能力,5 个关键能力都有所考查,因此关键能力赋值为5;考查要求是创新性,赋值为4;考查载体是探索创新情境,赋值为3.利用上述方法,对9 套试卷中的每一个题目进行赋值.

2.3 高考数学试题一级评价指标的信度检验

利用2.2 的赋值方法,得到9 套试卷的每个题目在5 个指标下的赋值,最后将这些指标赋值进行合计,得到9 套试卷在5 个指标下的总赋值得分,如表4所示:

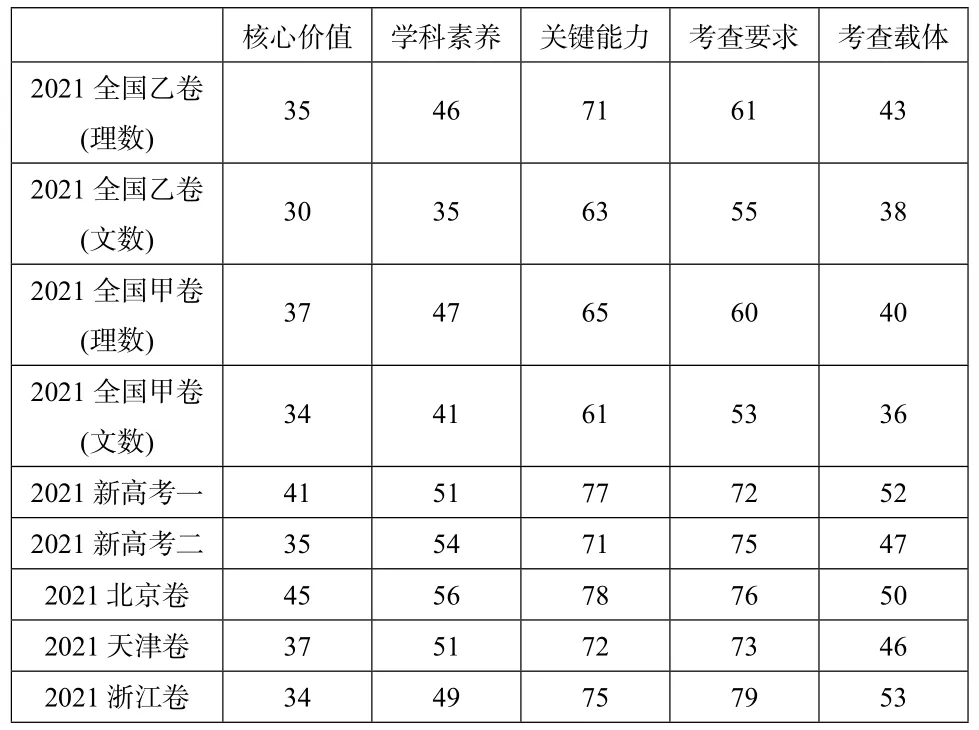
表4 9 套试卷的总赋值得分

由于各套试卷题目数量不尽相同,为了消除题目数量的影响,在此给每个总赋值得分除以相应的试卷题目数量,9 套试卷的题目数量分别是: 26、26、25、25、29、29、31、31、32(全国卷没有把选做题列入),进而得到表5,即9 套试卷的平均赋值得分:

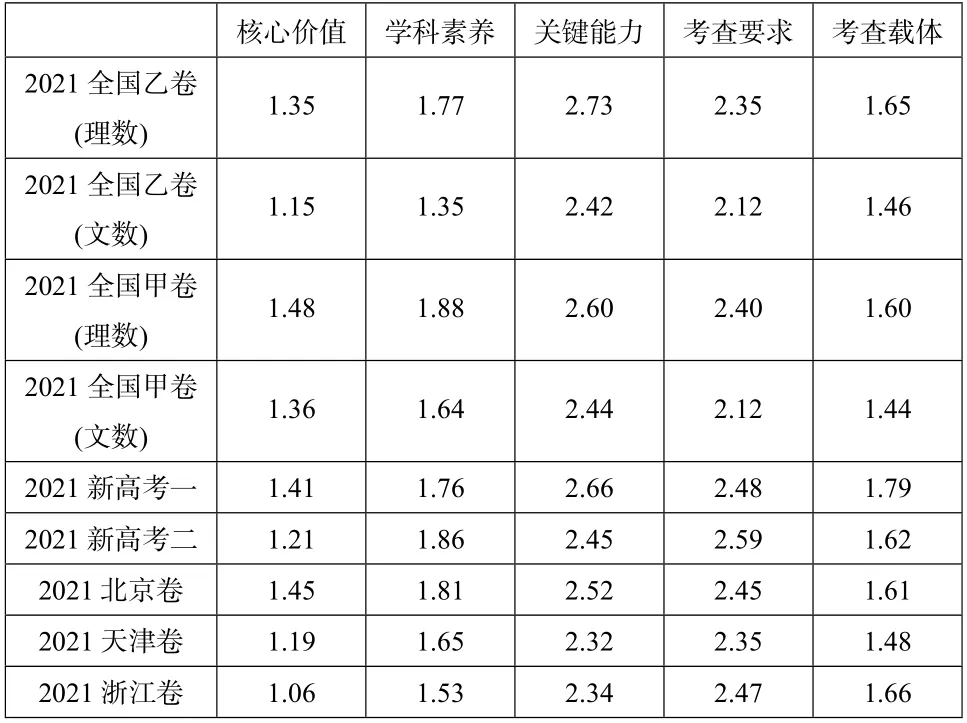
表5 9套试卷的平均赋值得分表

为了检验以上评价指标的合理性,本文进行了信度检验.本研究主要测量指标体系的内在信度.利用SPSS 软件对9套试卷的5 个一级指标的平均赋值得分进行信度分析,特别地,采用克朗巴赫(Cronbach)创造的α系数检验信度.α系数值介于0 与1 之间,α值越高,表明分项之间的一致性越强,内部一致性可信度越高,所得结果如表6:

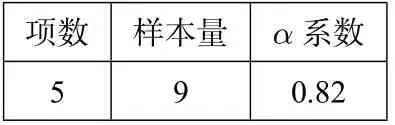
表6 α 系数信度检验表

从表6可以看到α系数为0.82,说明各分项评价指标的内部一致性较好,指标体系的信度是令人满意的.

2.4 各试卷一级评价指标的比较

为了更直观地体现9 套试卷在5 个指标下的差异,在此绘制了相应的平均赋值得分柱状图,如图4 所示:

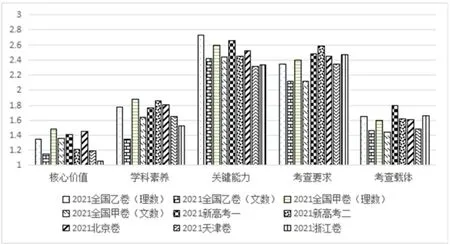
图4

从图4 可知核心价值指标中,平均得分最高的是全国甲卷(理数),其次是北京卷,最低的是浙江卷;学科素养指标中,平均得分最高的还是全国甲卷(理数),与新高考二卷基本持平,其次是北京卷,最低的是全国乙卷(文数);关键能力指标中,平均得分最高的是全国乙卷(理数),其次是新高考一卷,最低的是天津卷和浙江卷;考查载体指标中,平均得分最高的是新高考一卷,其次是全国乙卷(理数)和浙江卷基本持平,最低的是全国甲卷(文数).

另外从图中也能够直观看出关键能力、考查要求的得分比其他三个指标整体较高,这也能够反映出9 套试卷对这两个指标的考查比较综合,且要求较高,同一个题目会考查多个二级指标.

3 高考数学试卷综合评价模型构建与应用

3.1 熵权TOPSIS 法的简介及计算步骤

熵权法是一种客观的赋予权重的方法,它通过各个指标所提供的信息不确定性来确定各指标的权重,进而得到各个指标信息熵.熵值越小,无序程度越低,指标权重就越低,依据该规律可以确定各个指标的权重.指标的信息熵越小,该指标表达的信息不确定性越小,在综合评价中对决策的帮助反而更大,对应有较大的权重[9].

TOPSIS 综合评价法用于解决对象多属性决策问题,它的基本思想是选取评价对象在所有指标下的最优解和最劣解作为正负理想解(所谓正理想解是指设想的最好方案,它的各个属性值都达到各指标中最好的值,作为肯定的理想目标.而负理想解是另一设想的最坏的方案,作为否定的理想目标),检测评价对象各指标值与正负理想解间的距离,通过计算相对贴合度从而对现有对象进行排序与评价.最优结果为与肯定理想目标最近,与否定理想目标最远.该方法充分考虑研究对象某一指标值与样本中最高值及最低值的距离,表现的是一个相对的概念[10].

例如有m个评价对象,n个评价指标,则具体计算是:

第一步: 先将原始数据进行标准化处理,在这里将指标分为正向和负向两种指标,正向指标即效益性指标,负向指标即成本性指标.具体可利用公式(1)、(2):

其中vij表示第i个评价对象的第j个评价指标的原始值,xij为第i个评价对象的第j个评价指标的标准化值.

第二步: 计算指标标准化值的比重, 对标准化矩阵X= (xij)m×n中的各指标的标准化数据进行比重归一化处理,利用公式(3)

第三步: 计算各指标的熵值ej,利用公式(4)

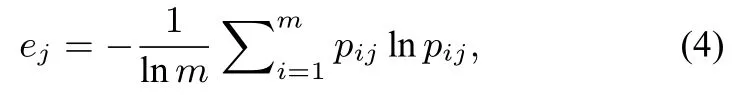
其中定义当pij=0 时,pijlnpij=0.

第四步: 计算各指标熵权kj,利用公式(5)

第五步: 建立加权标准化决策矩阵,利用公式(6)

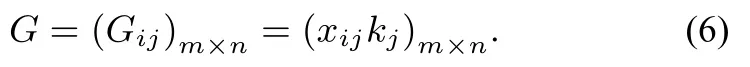
第六步: 确定正、负理想解,其中正理想解值的公式表示为:R+=(G+1,··· ,G+n), 负理想解R-=(G-1,··· ,G-n),利用公式(7)、(8):

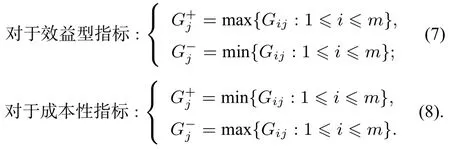
第七步: 计算欧氏距离,利用公式(9):

第八步: 计算相对贴近度,利用公式(10):

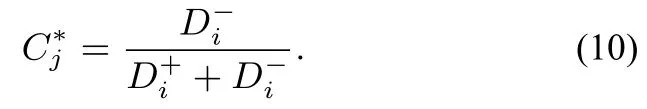
第九步: 待估对象排序:

根据第i个对象的D的贴近度大小,依次对各个对象进行排序[11].

3.2 一级评价指标的权重确定及信效度检验

在本文的高考数学试卷评价指标中涉及5 个不同的指标,通过2.4 的比较可以发现9 套试卷在各指标下的平均评价得分排序是不尽相同的,那5 个一级指标对总评价的影响是否相同呢? 基于以上的思考,本文利用熵权法对各指标的权重进行了研究.

具体的计算是将9 套试卷的5 个指标平均评价得分利用SPSSAU 在线数据分析软件进行熵权TOPSIS 分析,首先得到5 个指标的权重,如表7所示,然后进行了权重合理性T值检验,T值的计算公式为:

表7 高考评价各指标权重系数表

如果其值界于0.5-1 之间,指标越接近1,则权重分布越合理.

根据表7中的数据计算权重合理性检验值,T=表明各指标间的权重分布是非常合理的.

3.3 TOPSIS 综合评价排序

在得到5 个指标的权重后,利用公式(6),建立加权标准化决策矩阵,进一步利用TOPSIS 法基于理想解得到9 套试卷的综合评价排序,如表8所示:

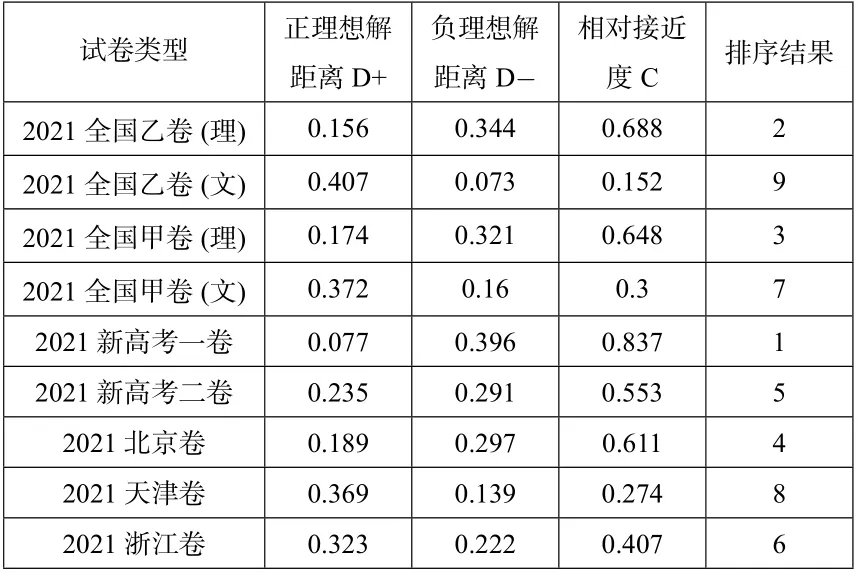
表8 TOPSIS评价计算结果

为了更直观地体现9 套试卷评价指标与理想解的贴近程度,在此绘制了相应的柱状图,如图5 所示:

图5

从图5 能够看出: 全国乙卷(文数)距离正理想解的距离最大,其次是全国甲卷(文数)与天津卷基本持平,距离最小的是新高考一卷.而新高考一卷距离负理想解的距离最大,其次是全国乙卷(理数),距离最小的是全国乙卷(文数).再看相对贴近度,贴近度最大的是新高考一卷,其次是全国乙卷(理数), 最小的是全国乙卷(文数), 说明新高考一卷、全国乙卷(理数)这两套试卷更接近正理想解,而全国乙卷(文数)离正理想距离最远.由此可见,这一结论在三个解释中是一致的.

从前边得到的5 个权重可以发现关键能力、考查要求、考查载体的权重相对较大,这也说明了新高考一卷、全国乙卷(理数)在这三个指标上较为突出,反之全国乙卷(文数)在这三个指标考查相对较弱.

其实这一结论在试题中也要直观的体现,例如新高考一卷的第7 题,此题设问简单,函数模型也是学生熟悉的常用指数函数,考点是切线问题.这道题目看似比较常规,但是却隐含着多个概念问题,像指数函数的图像、性质、切线、导数、斜率等,解答此题,需要学生联系函数与导数部分的多个知识内容,甚至极限的思想,有可能“小题大做”[12].再例如全国乙卷(理数)第12 题,要比较数值大小,需要合理构造函数,利用导数研究单调性,考查由特殊到一般设计构造函数能力,运算求解能力,需要考生有较强的理性思维、数学探索能力.

5 结语

5.1 评价模型进一步优化和完善试题评价方法

本研究以《中国高考评价体系》为理论基础和研究起点,构建适合数学学科的高考评价体系,并以此为分析工具,利用熵权法确定各指标的权重,构建了高考数学试题评价模型,最后利用TOPSIS 法对试卷评价进行综合排序.相比以往的试题评价方法,高考数学试卷评价模型更具有综合性,它将核心价值、学科素养、关键能力、考查要求、考查载体的评价融为一体,得到的试卷总评价更为全面、科学、合理.

5.2 评价模型对基础教育教学具有指导意义

通过研究这些试卷的命题特点,体会和领悟高考数学改革的方向,进而正确把握新高考数学的命题方向.通过对比9 套试卷,可以发现新高考数学卷题目背景较为丰富,涉及日常生产生活、文化艺术、社会热点、学科交叉等多种背景.将知识、素养、价值融于背景之中,升华知识的应用,让学生进一步感受到数学在生活中的实用价值、艺术价值等.这些改变都突出了高考评价体系倡导的“价值引领、素养导向、能力为重、知识为基”的评价理念,这将对一线教师的教育教学改革起到积极的引导作用.