M-矩阵最小特征值下界的新估计
刘兰兰,韩盼
(贵州民族大学 数据科学与信息工程学院, 贵州 贵阳 550025)
0 引言
非奇异M-矩阵是一类具有特殊结构的矩阵,是逆非负的一类Z-矩阵。M-矩阵的应用研究涉及到多个交叉领域的研究,例如在控制理论、工程计算、数字信号处理等多个研究领域都具有广泛的应用。关于非奇异M-矩阵最小特征值下界的研究一直是很多学者研究的热点,并且最近也给出了一个更好的结果[1-5]。本文继续在已有的基础上对非奇异M-矩阵最小特征值的更大的下界进行研究,给出新的下界。
1 预备知识
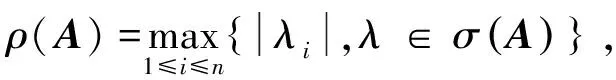
若B≥0,有A=sI-B,s>0,s>ρ(B),则称A为非奇异M-矩阵[7-15],记A∈Mn。
设A=(aij)∈Rn×n,如果存在一个置换矩阵T,使得
则称A是可约的,其中B、D都是阶数大于等于1的方阵,否则称A不可约。
设A=(aij)≥0为非负矩阵,令L=A-D,其中D=diag(a11,a22,…,ann),同时JA=R-1L,R=diag(r11,r22,…,rnn),其中
显然JA是非负矩阵,若对任意i∈N都有aii=0,则JA=A。
由文献[7]知:若A,B∈Mn,则A∘B-1∈Mn,矩阵A和B的Hadamard积定义为A∘B=(aijbij), 则A∘B-1=(aijβij)。
为了后面叙述方便,引入以下符号:
设A=(aij)∈Cn×n, 对任意的
文献[2]中给出了非奇异M-矩阵特征值的下界,估计式如下
(1)
文献[3]对特征值的下界做了进一步的研究得到的估计式如下:B=(bij)∈Cn×n是M-矩阵,且B-1=(βij),
(2)
孙德淑改进了文献[3]的结论,给出了更准确的下界估计式:设B=(bij)∈Mn,B-1=(βij),
(3)
(4)
陈付彬在文献[5]中给出了优于式(2)、(4)的估计式,其结果是对文献[3-4]的改进。其估计式如下:设B∈Mn, 且B-1=(βij),
(5)
(6)
2 主要结论
引理1[6]设A,B∈Cn×n, 且P,Q∈Cn×n是对角矩阵,则
P(A∘B)Q=(PAQ)∘B=(PA)∘(BQ)=A∘(PBQ)。
引理2[7]设A∈Mn, 则有Z=diag(zii),zii>0, 使得Z-1AZ是严格对角占优矩阵M-矩阵。
引理3[9]若B=(bij)∈Mn严格对角占优,B-1=(βij), 则βji≤uiβii。
引理4[8]设A∈Mn(C), 则对Mn(C)上任意矩阵范数‖·‖都有
ρ(A)≤‖A‖。

定理1设A≥0,B=(bij)∈Mn,且B-1=(βij),则
证明当n=1 时,定理成立,现在考虑n≥2时定理是否也成立。
因B∈Mn,由引理1和引理2知,存在对角矩阵Z=diag(z11,z22,…,znn),zii≥0,使得Z-1AZ是严格对角占优的M-矩阵,且
ρ(A∘B-1)=ρ(Z-1(A∘B-1)Z)=ρ(A∘(Z-1BZ)-1) 。
为了方便讨论和不失一般性,假设B∈Mn严格对角占优,且B>0,下面对A,B矩阵分两种情形进行证明。

②矩阵A、B至少有一个可约,则存在n阶置换矩阵F=(fij),其中f12=f23=f34=…=fn1=1, 其余fij=0, 则对任意正数ε, 让A+εF和B-εF均为不可约的矩阵。A+εF和B-εF分别代替A和B,当ε→0, 利用连续性可知结论成立。
定理2设B=(bij)∈Mn,B-1=(βij), 则
证明令定理1中,矩阵A的元素aij=1, 则aii=rii=1, 且ρ(JA)=n-1,A∘B-1=B-1,则有
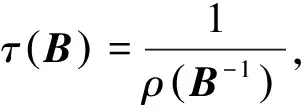
即定理得证。
定理3设A=(aij)≥0,B=(bij)∈Mn,B-1=(βij),则
证明当n=1 时,定理显然成立,下证当n≥2 时定理成立。不失一般性,仍然设B是严格对角占优的M-矩阵。
下面对A、B分为是否可约2种情形进行证明。
①矩阵A、B都不可约,由A非负不可约,得到ρ(JA)和ρ(JAT)也非负不可约,所以存在正向量y=(yi), 使得JATy=ρ(JAT)y, 根据JA的定义,可知
ρ(JAT)=ρ(R-1LT)=ρ(LR-1)=ρ(R-1(LR-1)R)=ρ(JA),
有
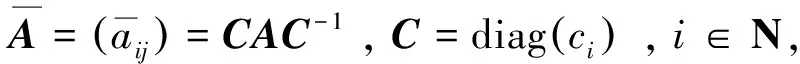
由引理1 知

(uiβiiρ(JA)rii)(ujβjjρ(JA)rjj),
即
(λ-aiiβii)(λ-ajjβjj)≤(uiβiiρ(JA)rii)(ujβjjρ(JA)rjj)。
解上述不等式,得
综上所述,得
②矩阵A、B至少有一个可约,则存在n阶置换矩阵F=(fij), 其中f12=f23=f34=…=fn1=1, 其余fij=0, 则对任意正数ε, 让A+εF是不可约非负矩阵,B-εF均为不可约的M-矩阵。A+εF和B-εF分别代替A和B,当ε→0, 利用连续性可知结论成立。
定理4设B=(bij)∈Mn, 且B-1=(βij), 则有
证明令定理3中,矩阵A中的元素aij=1,则aii=rii=1ρ(JA)=n-1,ρ(A∘B-1)=ρ(B-1), 所以
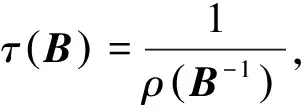
注1对定理2和定理4进行比较,不失一般性,让i≠j, 设
βjj+vj(n-1)βjj≤βii+vi(n-1)βii,
则
vj(n-1)βjj≤βii-βjj+vi(n-1)βii。
所以
βii+(n-1)viβii。
因此
综上所述,定理4的结果优于定理2的结果。
注2对定理4和文献[5]中的定理4进行比较。
由文献[5]知,1>dj>sji>wji>0,j≠i,j∈N, 因此
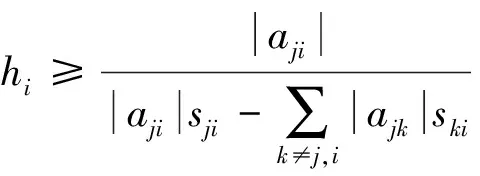
而
由sjihi≥wji可知ei≤1,所以
sjihi≥wjiei。
当且仅当是上式取等号.
其中B-1=(βij)。综上所述,定理4的结果比文献[5]中定理4优越。
3 数值算例
例1设B1为M-矩阵,则
例2设B2为M-矩阵,则
例3设B3为M-矩阵,则
借助MATLAB软件可以得到如下结果。将以上3个算例与文献[2-5]中的数值结果和文本定理2和定理4的结果进行对比,对比结果见表1。

表1 B的特征值的下界Tab.1 Lower bound of B
本文给出了M-矩阵最小特征值的新下界的估计式,从表1可以看出:定理2和定理4的数值结果是τ(B)的有效上界,且比文献[2-5]的结果更接近于真值,因此文中提出的新估计式要优于上述文献中已有的估计式。

