欺骗攻击和脉冲干扰下的符号网络二分同步
卢月, 张小美*, 盛苏英
( 1.南通大学 信息科学技术学院, 江苏 南通 226019;2.南通大学 电气工程学院, 江苏 南通 226019)
0 引言
在过去的20年里,复杂网络的同步[1]以及多智能体系统的一致性[2]得到了广泛的研究,其中原因之一是其在诸如机器人控制[2]和网络物理微电网[3]等领域中的广泛应用。注意到以上文献关于复杂网络与多智能体系统的协调控制问题研究是以刻画邻居节点之间通讯连接的边权值都是正的为假设条件而展开的,然而,实际情况未必都是这样,例如,意见形成的分布式过程[4]。在存在合作和竞争关系的网络中,刻画邻居节点之间通信连接的边权值既可以是正的也可以是负的[5]。目前,多智能体网络的二分同步/一致性问题研究包括无通信时滞的线性智能体[6]、有通信时滞的线性智能体[7]、无通信时滞的非线性智能体[8-9]、有通信时滞的非线性智能体[10]、量化通信的非线性智能体[9]、间隙通信的非线性智能体[10]和脉冲通信的非线性智能体[11]等。特别地,文献[11]研究了符号网络中耦合的神经网络基于分布式脉冲协议的拟二分同步问题。此外,脉冲对复杂网络同步的影响有2种情况:一是干扰,对同步起负面作用[12];二是控制输入,对同步起正面作用[13]。
一般来讲,现实世界中的脉冲有2类,即确定性脉冲[12-14]和随机脉冲[15]。对于有脉冲影响的多智能体网络的同步/一致性问题,大部分现有的研究是针对确定性脉冲进行的,即脉冲的强度和密度都是确定性的。特别地,确定性脉冲影响下的多智能体网络的二分协同问题近年来得到了研究[11,16-17]。文献[15]研究了符号网络中耦合的分数阶神经网络在确定性脉冲影响下的拟二分同步问题。文献[16]研究了合作-竞争网络中二阶非线性多智能体系统在确定性脉冲影响下的二分编队问题。从现有文献不难发现,针对确定性脉冲影响下的多智能体网络的协同问题研究已取得大量的研究成果,而随机脉冲影响下的多智能体网络的协同问题的研究成果则很少。文献[17]研究了存在脉冲影响的非线性时滞多智能体系统当脉冲强度以一定的概率发生变化时的一致跟踪问题。
近年来,网络化控制系统的安全控制问题[18],特别地,多智能体网络的安全同步控制问题[4,19-20]引起了人们极大的研究兴趣。文献[4]研究了自主交流微电网在传感器和执行器均遭受欺骗攻击的情形下基于分布式鲁棒自适应控制策略的电压和频率调节问题。文献[19]研究了重放攻击和拒绝服务攻击下的多智能体系统基于事件驱动机制的领跟随一致性控制问题。文献[20]在脉冲控制的框架下研究了遭受欺骗攻击的多智能体系统的安全同步问题。文献[21]研究了欺骗攻击下非线性时滞多智能体系统基于脉冲控制的一致性容错跟踪问题,并且脉冲强度是时不变的。同时也注意到,针对欺骗攻击下基于符号网络的多智能体系统的二分同步控制问题的研究成果还较少[22-23]。文献[22]研究了传感器遭受恶意攻击下执行器饱和的非线性多智能体系统基于连续时间控制策略的二分输出跟踪问题。文献[23]针对符号网络中异质多智能体系统研究了其基于连续时间输出反馈控制的二分状态同步问题,同时考虑了跟随者的因物理部件受到攻击而引入的对抗性输入。
从以上讨论不难发现,现有的文献只针对诸如对抗性攻击[22-23]或确定性脉冲[12]单一因素影响下的二分同步/一致性问题进行研究的。 然而,实际的信息-物理网络中可能会同时存在恶意的信息-物理攻击、确定性脉冲或随机脉冲。本文中提出的Lipschitz型符号网络的脉冲系统模型,同时考虑随机脉冲强度的脉冲干扰和欺骗攻击的随机发生;在考虑通讯连接存在时滞交互的情形下,给出符号网络达到二分同步的充分条件。
1 预备知识和问题描述
1.1 符号图理论
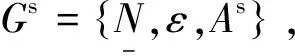

Ls=Ds-As,
(1)
式中,
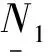
并且
则称符号图Gs是结构平衡的;否则,称符号图Gs为结构不平衡。
1.2 问题描述
考虑如下Lipschitz型符号网络:
(2)



注1文献[25]中指出,物理攻击可能会导致xi(t)在tk发生突然变化。该现象在数学上被描述为网络 (2)中的脉冲干扰。不同于文献[25]中的确定性脉冲,本文考虑具有随机强度的脉冲干扰。此外,假设欺骗攻击随机发生在各脉冲时刻,并利用Bernoulli分布序列刻画欺骗攻击的随机发生现象。
根据 Laplacian 矩阵Ls的定义,公式 (2)可写成
(3)
假设1对于任意的m∈{1,2,…,nx},fm(·)是奇函数,满足:
|fm(a)-fm(b)|≤νm|a-b|,∀a,b∈R,
式中νm>0为已知的常数。
假设2h(·)∈Rnx是奇函数,满足
‖h(z1)-h(z2)‖≤θ‖z1-z2‖, ∀z1,z2∈Rnx,
式中θ>0为已知的常数。
假设3符号图Gs是结构平衡的。
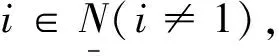
式中,
则称符号网络(3)是二分同步的。
因此,在假设3下,式(3)变为
(4)
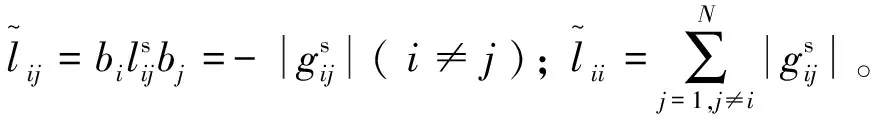
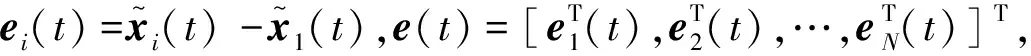
(5)
则有
(6)

定义3平均脉冲间隔[26]如果存在正整数N0和正数Ta使得下式成立:

引理1[27]假设非负函数V(t),t∈[-τ,∞)满足
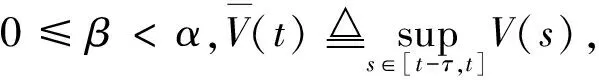
式中γ>0是方程γ-α+βeγτ=0的唯一解。
2 主要结果
定理 1如果对于常数λ>ε>0,γ>1,存在正定矩阵P>0, 常数δ>0,r>0,使得下面的不等式成立:
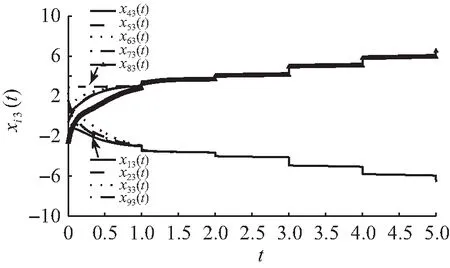
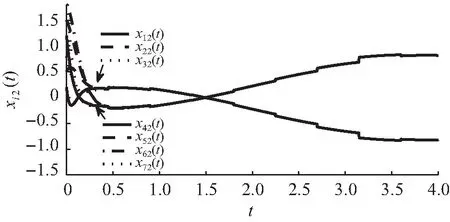
P (7) (8) (9) (10) (11) 则符号网络(3)当平均脉冲间隔不小于Ta时是二分同步的。 证明由假设1可得 φT(t)φ(t)-eT(t)(IN-1⊗ΥTΥ)e(t)≤0, (12) 式中,Υ=diag{ν1,ν2,…,νnx}。 构造Lyapunov候选函数如下: V(t)=eT(t)Pe(t)。 (13) 当t∈[tk-1,tk)时,沿着系统(3) 的轨迹对V(t)求导,并利用公式(12),可得对于任意的正数δ>0,λ>ε>0,有 ξT(t)Ωξ(t)-λV(t)+εV(t-τ(t)), (14) 式中ξ(t)=[eT(t)φT(t)eT(t-τ(t))]T。 由公式(8)、(14)可得 (15) 由引理1得 (16) 式中α满足公式(11)。 当t=tk时,由公式(16)得 (17) 由假设2可得 (18) (19) 式中λmax(P)表示矩阵P的最大特征值。 由公式(17)、(19)得 (20) 由公式(7)、(9)、(20)得 (21) 因此,当t∈[tk-1,tk)时,有 (22) 利用定义3,可得当t∈[tk-1,tk)时,有 (23) 这意味着 (24) 由公式 (10) 得 (25) 由定义 2、3可知,符号网络(3)当平均脉冲间隔不小于Ta时是二分同步的。 注2不同于文献[20,21],其在具有确定性脉冲强度的脉冲的控制框架下研究了多智能体系统在传统意义下的安全同步问题,本文则研究的是存在具有随机脉冲强度的脉冲干扰情形下合作竞争网络的安全二分同步问题,即在研究的对象和研究的网络环境两方面均不同于文献[20,21],拓展了多智能体系统一致性控制的研究内容。 如果网络(2)中不考虑欺骗攻击,则公式(2)变为 (26) 相应的误差系统(6)变为 (27) 推论 1如果对于常数λ>ε>0,γ>1,存在正定矩阵P>0, 常数δ>0和r>0, 使得下面的不等式成立: P (28) (29) (1+2ϑ+χ-γ)P<0, (30) (31) α满足 (32) 则平均脉冲间隔不小于Ta时,符号网络(26)是二分同步的。 例1考虑由9个蔡氏电路构成的网络(2),式中参数矩阵A、B和非线性函数f(xi(t))与文献[8]中的相同,即 xi(t)=[xi1(t),xi2(t),xi3(t)]T,f1(xi1(t))=0.442(|xi1(t)+1|-|xi1(t)-1|)。 容易验证下面的关系式成立: |f1(a)-f1(b)|≤ν1|a-b|,∀a,b∈R, 式中ν1=0.884。 网络(2)的拓扑与文献[8]中的一样,由9个节点组成的符号图如图1所示。 图1 由9个节点组成的符号图Fig.1 Symbol graph composed of nine nodes 假设h(xi(t))=[0.3xi1(t),-0.3sin(xi2(t)),tanh(0.3xi3(t))]T, 则 ‖h(z1)-h(z2)‖≤θ‖z1-z2‖,∀z1,z2∈R3, 式中θ=0.3。 令 利用MATLAB 2016年软件并结合CVX凸优化工具箱求解定理1中的线性矩阵不等式 (7)—(9),可得其可行解。由定理1可知该符号网络是二分同步的。在仿真中取tk-tk-1=1 s。图2—图4表明该符号网络可以实现二分同步。 图2 状态xi1(t)(i=1,2,…,9)的轨迹Fig.2 Trajectories of states xi1(t)(i=1,2,…,9) 图3 状态xi2(t)(i=1,2,…,9)的轨迹Fig.3 Trajectories of states xi2(t)(i=1,2,…,9) 图4 状态xi3(t)(i=1,…,9)的轨迹Fig.4 Trajectories of states xi3(t)(i=1,…,9) 例2考虑由7个混沌个体构成的网络(2),式中 容易验证下面的关系式成立: |fm(a)-fm(b)|≤|a-b|,∀a,b∈R,m=1,2,3。 网络(2)的拓扑与文献[16]中的一样,由7个节点组成的符号图如图5所示。 图5 由7个节点组成的符号图 则符号图5结构平衡,并且包含有向生成树。 图6 状态xi1(t)(i=1,2,…,7)的轨迹Fig.6 Trajectories of states xi1(t)(i=1,2,…,7) 图7 状态xi2(t)(i=1,2,…,7)的轨迹Fig.7 Trajectories of states xi2(t)(i=1,2,…,7) 图8 状态xi3(t)(i=1,2,…,7)的轨迹Fig.8 Trajectories of states xi3(t)(i=1,2,…,7) 注3上述2个仿真数值例子验证了定理1所给出的抗脉冲干扰和欺骗攻击的二分同步的充分条件的有效性。本文的主要结果可进一步应用到网络化机器人系统的二分同步控制[28]中。 本文研究了有向符号图下Lipschitz型多智能体系统在随机脉冲干扰和欺骗攻击影响下的二分同步问题。在欺骗攻击随机发生在各脉冲时刻的假设下,利用规范变换和Lyapunov稳定性理论,以线性矩阵不等式和代数不等式的形式给出了实现二分同步的充分条件。本文假设了所有邻居智能体可以同时获得通信网络的使用权限并传输对应数据。未来的研究工作之一是研究诸如 Round-Robin协议等通信协议影响下非线性多智能体符号网络的二分同步问题。
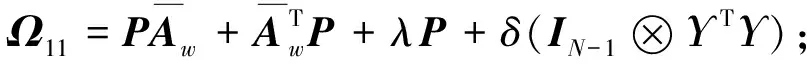



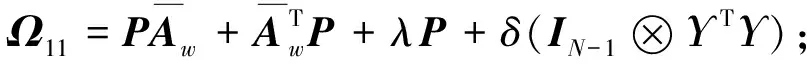
3 数值例子


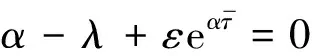



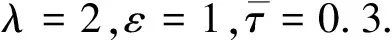



4 结语

