伪惯导建模的极区双速度模式惯性系对准算法

李 杨, 刘 猛, 宫 京, 王永召, 邓福建

(1. 海军研究院, 北京 100161; 2. 天津航海仪器研究所, 天津 300131;3. 中国船舶航海保障技术实验室, 天津 300131)

0 引 言

随着全球变暖,极区活动将日益频繁。极区导航是运载工具在极区安全可靠航行的保障。然而,极区特殊的地理、电磁、气象、天文条件下,常用的导航方法(例如,地磁、无线电、天文、卫星导航等)在极区不能总是正常工作。不依赖外部环境的惯性导航设备则成为极区导航的重要技术手段。对于极区惯导系统,游移、格网、横向以及伪类地坐标系的惯导算法已经被提出,用于解决传统指北惯导在极区导航解算过程中所面临的问题。然而,极区初始对准仍是一个亟待解决的问题。

捷联惯性导航系统(strapdown inertial navigation system,SINS)初始对准通常分为两步完成:粗对准和精对准。粗对准是粗略获取载体的初始姿态矩阵,为接下来的精对准提供初始条件。高精度的粗对准可以为精对准提供一个更好的初始条件,保证精对准阶段的对准性能以及可靠性。基于矩阵分解的惯性系初始对准算法是一种常用的SINS粗对准算法,其在抑制外界干扰、对准快速性等方面的特别优势,国内外已经进行了大量的研究。此外,根据自主性要求,SINS行进间对准过程中通常选择里程计(odometers，OD)、多普勒(Doppler velocity logs, DVL)、计程仪等作为外部辅助设备,通常仅可以提供相对于载体系的外部速度信息,即。因此,本文针对辅助的SINS极区行进间惯性系粗对准算法进行研究。当载体航行在高纬度极地地区时,传统辅助的惯性系对准算法所面临的问题主要有两个方面:

(1) 传统基于地球经纬度编排的指北惯导系统的导航误差中含有随纬度成正切函数增加的误差项,从而在高纬度极地地区,其导航误差会被急剧放大,则传统指北惯导编排的惯性系初始对准在极区对准时,惯导建模失效将影响其对准性能。因此,需要考虑采用其他惯导建模来完成其对准过程。

(2) 随着纬度的升高,重力矢量与地球自转矢量逐渐共线,从而依靠其非共线原理完成辅助的行进间惯性系初始对准,在高纬度极地地区时,SINS方位失准角的可观测性变得非常弱。如果初始对准算法中存在模型误差,则必须考虑对其进行解决,否则其将可能影响初始对准的精度,进而影响接下来的精对准以及导航性能。而传统辅助的行进间惯性系初始对准算法在完成SINS初始对准过程时存在某些忽略项,从而不可避免地存在原理性模型误差,故必须考虑对其进行解决。

针对上述问题,本文采用基于伪类地坐标系的惯导力学编排方案(伪惯导建模)来解决传统指北惯导算法在高纬度极地地区误差放大问题;同时利用双速度模式惯性系初始对准算法来解决传统辅助对准算法中存在模型误差问题;最后,通过低纬度车载半实物仿真以及极区对准仿真试验对伪惯导建模的双速度模式极区惯性系对准算法进行验证。

1 基于伪类地坐标系的伪惯导建模编排方案

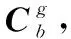
伪类坐标系是根据载体所在的初始经纬度(,)进行构建的,其与经典的地球坐标系(系,)存在如下关系:

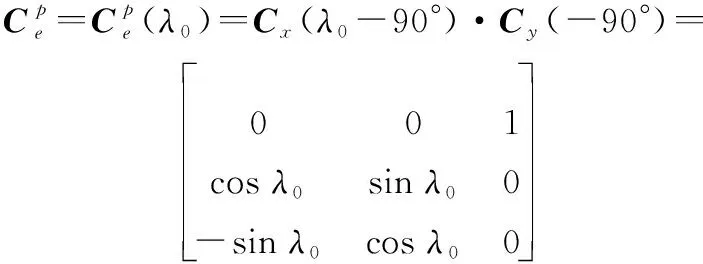
(1)

如图1所示,在伪类地球坐标系,其坐标原点仍为地球中心,而伪赤道则与载体初始位置所在的子午圈是重合的;其中,为伪北极点,轴与原重合,轴是指向载体初始位置在赤道平面的投影点,在赤道平面内垂直于轴。

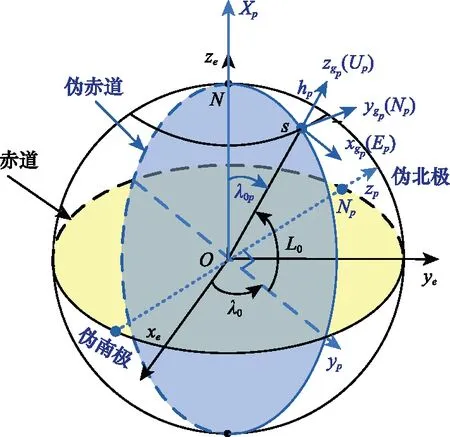
图1 伪类地球坐标系Fig.1 The pseudo Earth frame

同样,类似于传统的地球坐标系,在伪类地坐标系中,也定义了伪经纬度(,)和伪地理坐标系(系)。则根据定义,易得载体的初始伪位置( 0, 0)以及系和系之间的转换矩阵为

[ 0, 0]=[90°-, 0°]

(2)

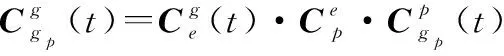
(3)

其中,

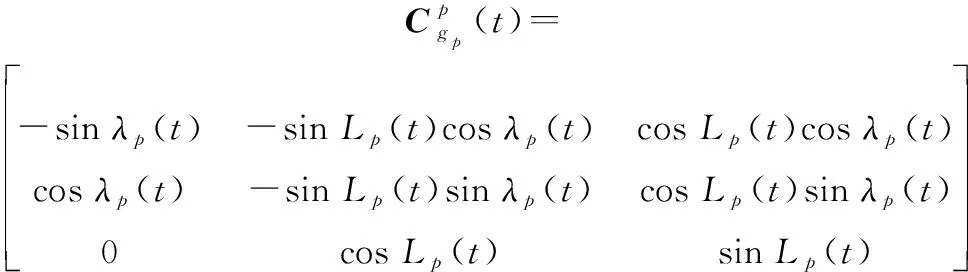
(4)

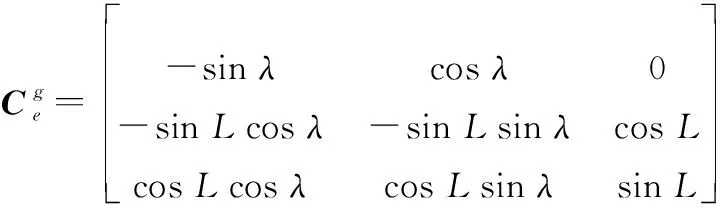
(5)

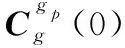
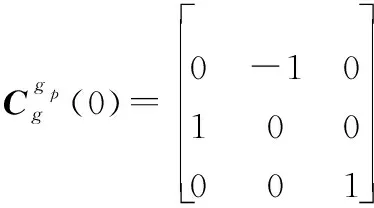
(6)

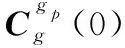
基于伪类地坐标系编排的SINS伪惯导建模则类似于传统指北惯导建模过程如下:

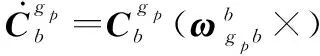
(7)

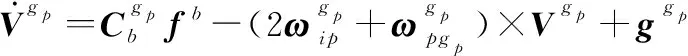
(8)

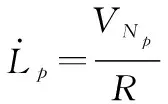
(9)

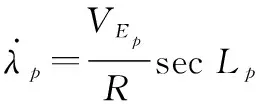
(10)

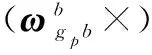
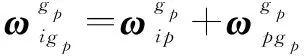
(11)

(12)

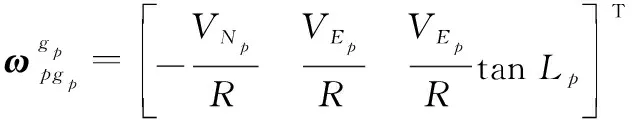
(13)

式中:为地球自转角速率。

2 伪惯导建模的极区双速度模式惯性系对准算法

2.1 伪惯导建模Vb辅助的惯性系对准算法

当采用伪惯导建模来实现SINS极区惯性系初始对准过程时,则以系作为惯导系统的导航坐标系。类似传统指北惯导建模的辅助SINS行进间惯性系对准算法,伪惯导建模辅助的SINS行进间惯性系粗对准算法的速度观测矢量构造方程可以写为

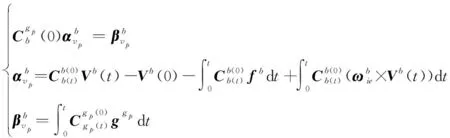
(14)

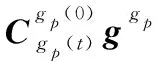
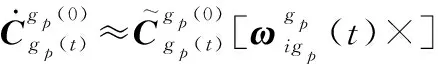
(15)

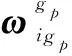
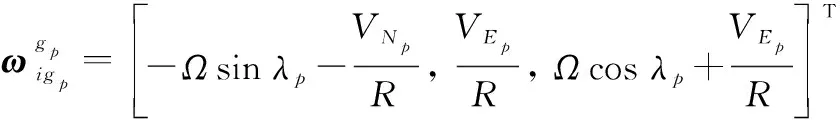
(16)

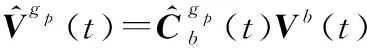
(17)

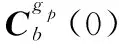
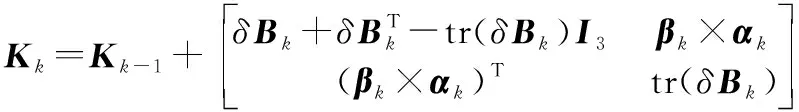
(18)

其中,

(19)

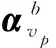
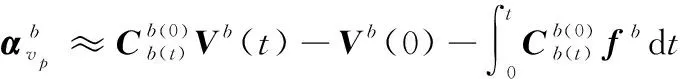
(20)

综上,由式(14)和式(20)可以得到伪惯导建模辅助的惯性系粗对准算法的速度矢量观测方程,进而由式(18)实现SINS的极区惯性系对准。

2.2 伪惯导建模的双速度模式惯性系对准算法

由上文可知,在实施伪惯导建模的传统辅助惯性系粗对准算法时,存在忽略项。然而,极地地区重力矢量与地球自转矢量逐渐共线,SINS的方位失准角的可观测性非常弱,从而方位对准对系统误差特别敏感,很容易引起对准系统的发散,故必须考虑对其进行解决,同时提高对准精度。文献[19]提出了采用双速度模式的多级惯性系对准算法,可以消除其模型误差,且不牺牲对准精度的稳定性。因此,本文采用伪惯导建模的双速度模式多级惯性系对准算法,消除SINS极区行进间对准的惯导建模问题以及对准模型误差问题,提高极区惯导对准的性能。

由伪惯导建模的速度方程式(8),移项整理得

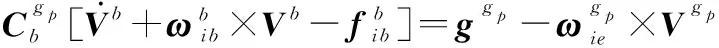
(21)

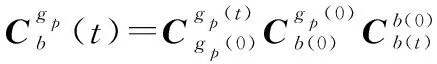
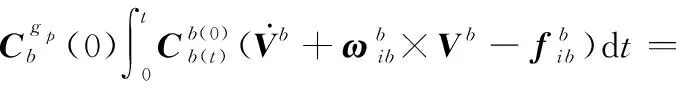
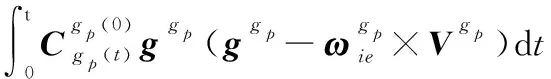
(22)

对式(22)等号左侧进行积分计算以及化简,则可以构造伪惯导建模的双速度模式惯性系对准算法的速度观测矢量方程如下:

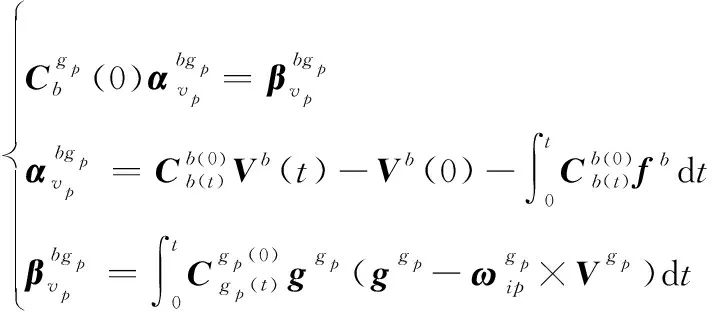
(23)

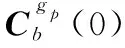
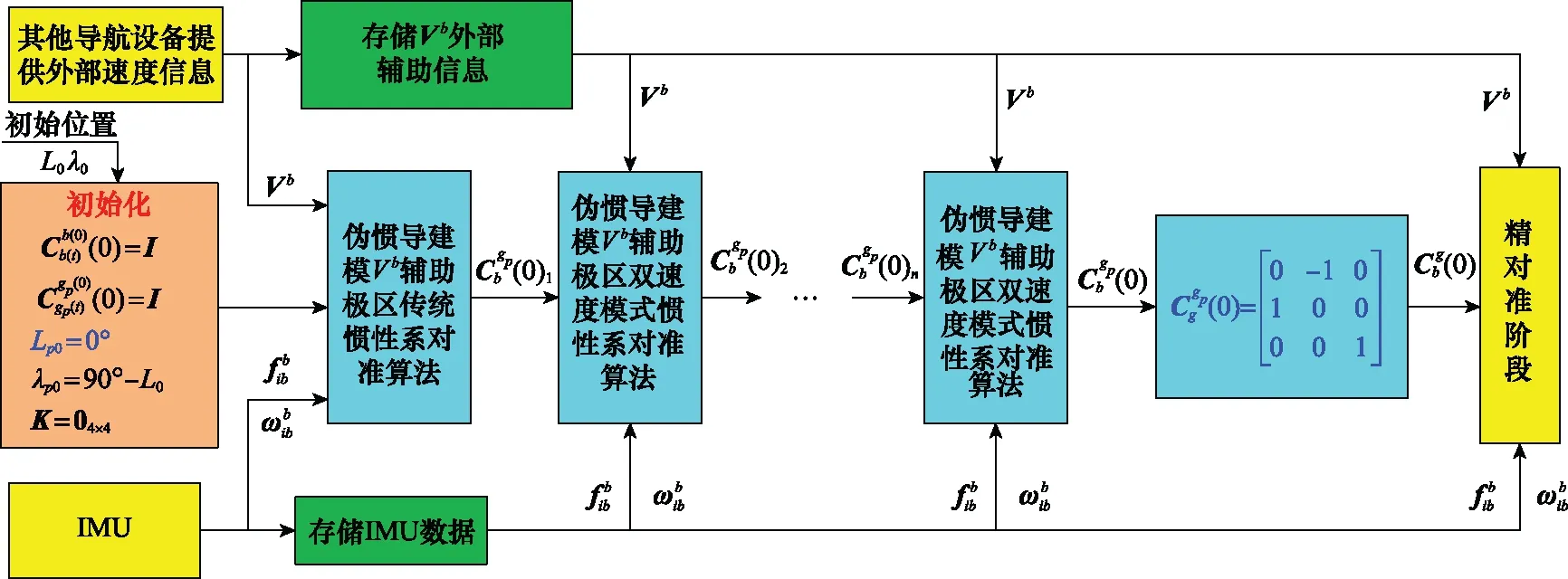
图2 伪惯导建模的双速度模式多级惯性系对准算法Fig.2 Multistage double-velocity inertial-frame alignment with the pseudo INS modeling

3 仿真与试验

3.1 低纬度半实物车载仿真试验

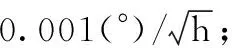
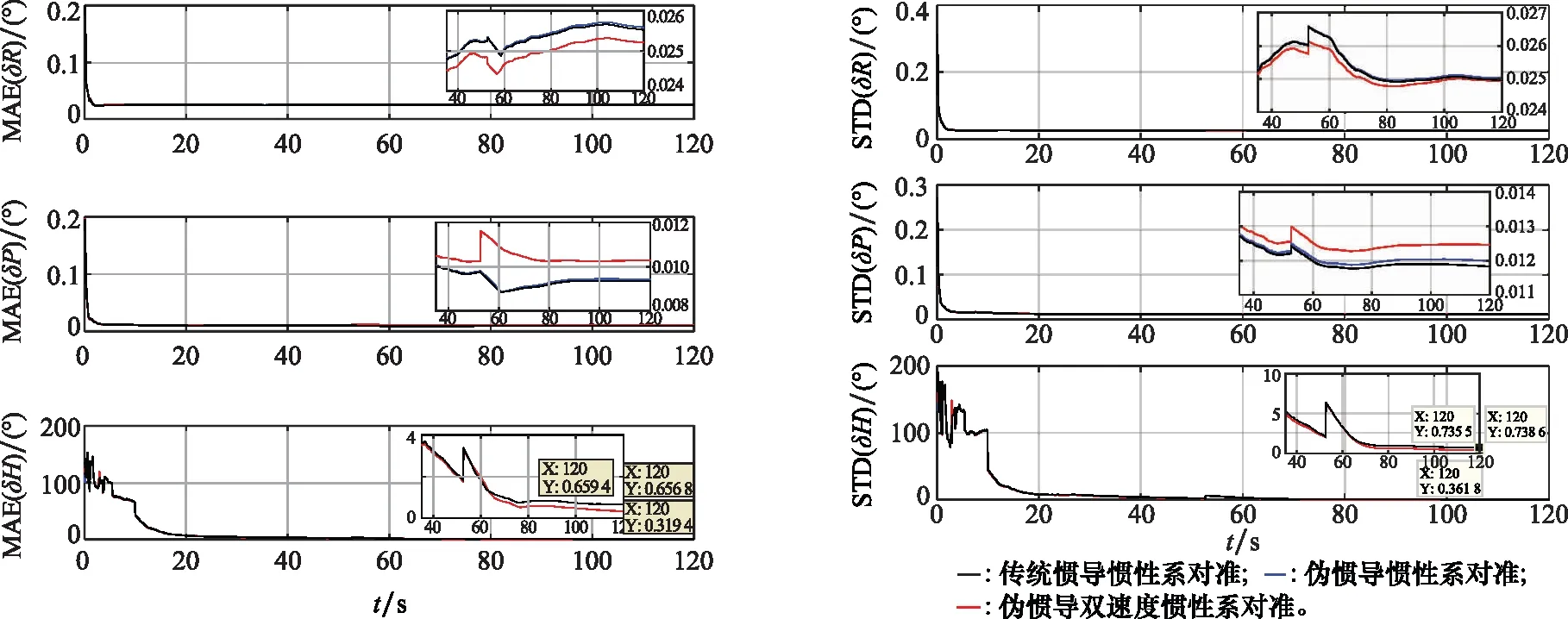
图3 姿态矩阵的MAEFig.3 MAE of the attitude matrix 图4 初始姿态矩阵的STDFig.4 STD of the initial attitude matrix

表1 10次初始姿态矩阵对准误差的数据统计

由图3和图4可知,采用3种对准算法,对准误差曲线随时间而逐渐收敛,在初始对准结束120 s时,3种惯性系对准算法航向误差MAE和STD分别为0.695 4°、0.656 8°、0.319 4°和0.738 6°、0.735 5°、0.361 8°。传统地球坐标系惯性系对准与伪惯导建模惯性对准算法具有几乎相同的对准精度,故采用伪惯导建模解决极区对准惯导建模问题是可行的。同时,采用伪惯导建模的双速度模式对准算法,具有更高的对准精度。这是由于双速度模式对准算法可以消除辅助惯性系对准算法中存在的模型误差问题,从而具有优越的性能。此外,由表1所示,对比3种算法的对准统计结果,再次验证伪惯导建模双速度模式极区行进间惯性系对准算法可以用于解决极区对准的惯导建模问题,同时解决传统算法的模型误差问题,有望消除SINS极区行进间对准的惯导建模问题以及对准模型误差问题,提高极区惯导对准的性能。

3.2 高纬度极区仿真试验

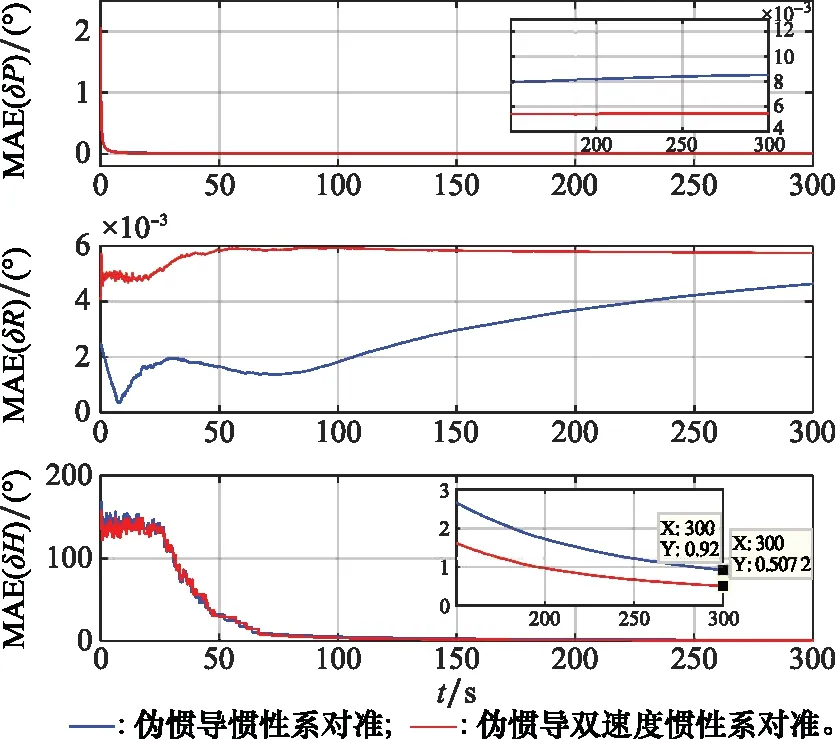
图5 75°纬度50次对准姿态矩阵的MAEFig.5 MAE of 50 alignment errors for attitude

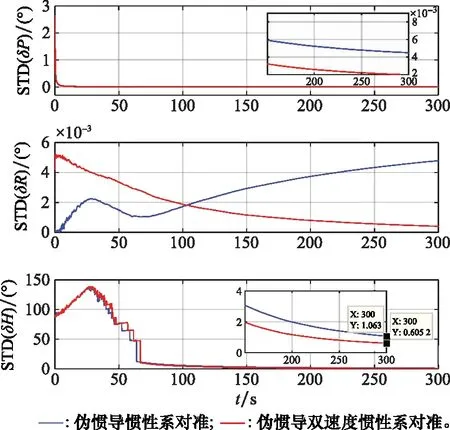
图6 75°纬度50次对准姿态矩阵的STDFig.6 STD of 50 alignment errors for attitude

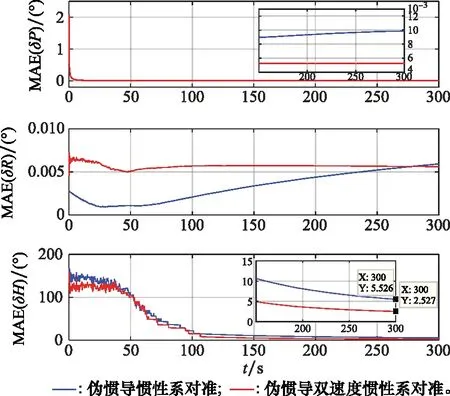
图7 85°纬度50次对准姿态矩阵的MAEFig.7 MAE of 50 alignment errors for attitude matrix

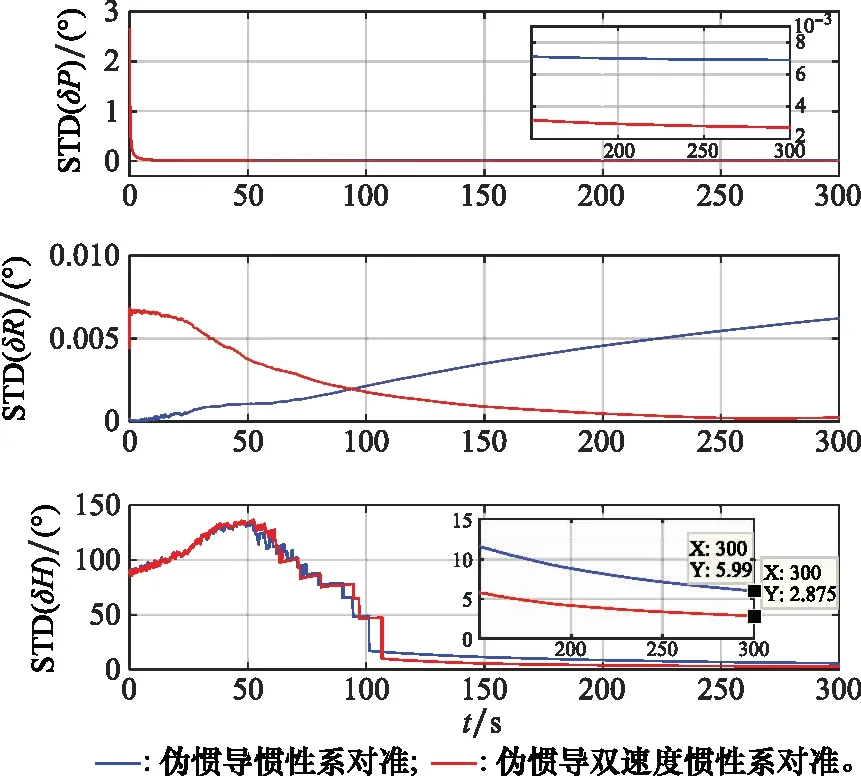
图8 85°纬度50次对准姿态矩阵的STDFig.8 STD of 50 alignment errors for attitude

由图5～图8可知,基于伪惯导建模的两种辅助的SINS惯性系对准算法在高纬度地区对准时,三轴对准误差逐渐收敛。在初始对准结束时,采用传统辅助的SINS惯性系对准算法和双速度模式多级惯性系对准算法在75°和85°初始纬度300s时刻的50次航向对准结果的平均绝对误差分别为0.920 0°、5.525 9°和0.507 2°、2.527 3°,标准差分别为1.063°、5.99°和0.605 2°、2.875°,可以满足精对准阶段的小角度线性误差模型假设应用要求。此外,显然采用双速度模式多级惯性系对准算法具有更高的对准精度。进而由表2可知,其相同的结论仍是可以得到。因此,本文所提的伪惯导建模辅助的双速度模式惯性系对准算法可以用于SINS高纬度极地地区的粗对准,并具有优越的性能。

此外,对比图5～图8容易看出,随着纬度升高其对准精度在逐渐下降。这是由于随着纬度升高,地球自转矢量与重力矢量逐渐共线,从而造成对准精度下降,特别是在极点及其附近将无法实现辅助SINS初始对准过程。因此,辅助SINS自对准初始对准算法仅可以完成SINS在全球大部分范围的初始对准,然而并不能实现极点及其附近的初始对准任务。

表2 50次伪惯导建模双速度模式惯性系对准算法的航向对准误差统计

4 结 论

针对辅助的极区SINS行进间粗对准问题,本文提出了伪惯导建模的双速度模式惯性系对准算法。首先详细介绍采用伪惯导建模实现SINS极区对准的优越性能,可以完全消除由导航误差放大而造成的极区对准影响,解决极区对准惯导模型问题,同时也方便实施。其次,分析了基于伪惯导建模传统辅助的惯性系粗对准算法实施过程以及在极区存在的问题,提出采用伪惯导建模双速度模式的惯性对准算法实现极区对准,消除其对准模型忽略误差项,提高极区对准精度。最后,通过低纬度车载半实物仿真试验以及极区对准仿真试验对其进行验证。试验结果表明:本文所提算法是可行且合理的,可以解决极区惯导建模以及对准模型中所存在的问题,提高极区对准的性能。然而,随着纬度升高,地球自转矢量与重力矢量逐渐共线,从而依靠其共线原理实现其辅助惯性系对准算法,将无法实现极点及其附近对准过程。故如要解决SINS全球粗对准问题,仍需要考虑采用其他方法完成。