基于新最速下降法的目标跟踪算法

王 帅, 向建军, 彭 芳, 唐书娟

(空军工程大学航空工程学院, 陕西 西安 710038)

0 引 言

跟踪的主要任务是实现对运动目标状态的连续估计。在军用和民用领域目标跟踪都有着重要的应用。常用的目标跟踪方法有Kalman滤波、交互多模型(interacting multiple model, IMM)滤波、多项式拟合等。

Kalman跟踪算法利用雷达来捕获运动目标测量数据,利用这些数据来估计运动目标的位置、速度、加速度等参数,实现对动目标的自动跟踪。但是Kalman算法仍然具有很多局限性,例如:受非线性误差影响大、要求非线性函数必须可导、要求系统是平稳随机过程等。同时模型具有单一性和不完整性。对此又研究出了许多改进模型,其中Blom等人提出了适用范围广的IMM跟踪算法。

IMM滤波算法是一种自适应滤波算法,它在跟踪中使用多种模型来描述不同的运动状态,通过有效的系统加权进行融合,在运动状态不固定的情况下也适用。多种模型中采用较多的是匀速直线运动(constant velocity, CV)模型、匀加速直线运动(constant acceleration, CA)模型、匀速圆周运动(constant turn, CT)模型、当前统计(current statistical, CS)模型等。IMM虽然具有应用范围广的优势,但是其仍然存在运算量大、计算复杂、机动情况下模型切换延迟的缺点。

对此本文提出一种新最速下降法的目标跟踪算法,该算法首先提出了一种运动模型,该模型属于一种改进的多项式拟合模型,多项式拟合具有易实现、计算简单和适用范围广的优点。接下来该算法采用一种新最速下降法来求解运动模型的最优参数,通过实时的最优运动模型对运动目标的航迹进行预测跟踪。实质上是用一种新最速下降法来求解多项式的参数,利用多项式来拟合目标的运动轨迹,达到跟踪预测的目的。经仿真验证,该算法具有易于工程实现、计算量小、适用范围广、计算精度高等优点。

1 IMM

IMM是Blom在基于伪贝叶斯方法的基础上提出的,具有里程碑式的意义。该模型是一种基于状态估计的运动模型集合,集合中包含了多种运动模型,每个运动模型都具有其相应的滤波模型和概率,此概率称为转移概率,通过马尔可夫矩阵的方式完成模型之间的相互转换。

IMM主要包括4部分:输入交互、Kalman滤波预测、更新模型概率、交互输出。其算法流程如图1所示。

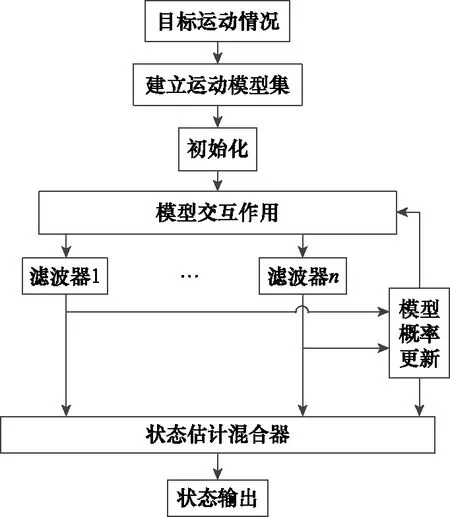
图1 IMM算法流程图Fig.1 Flow chart of IMM algorithm

2 基于新最速下降法的跟踪模型

本文提出基于一种新最速下降法的自适应目标跟踪算法。首先是建立运动的描述模型,再建立运动模型与实际运动之间的误差函数,通过新最速下降法求解运动模型的最优权系数,通过运动模型对目标进行跟踪和预测。

2.1 建立运动模型

目标在空间中的运动可以分解到,,3个二维平面上,分别对3个平面进行跟踪滤波,对3个平面进行处理之后,再将3个平面的运动联合起来便构成了空间运动,实现了对空间中运动目标的跟踪滤波。所以本文提出的运动模型将把平面作为示例进行解释。

目标在平面的运动是一条曲线,该曲线可以用多项式进行拟合,目标运动状态越复杂,曲线越多样,拟合所需要的多项式的阶次越高。例如:匀速运动只需要一阶多项式就可以拟合,匀加速运动需要二阶多项式才能拟合,以此类推复杂运动就需要高阶多项式来拟合。所以根据实际中目标的运动状态,提出一组状态描述多项式,如下式所示:

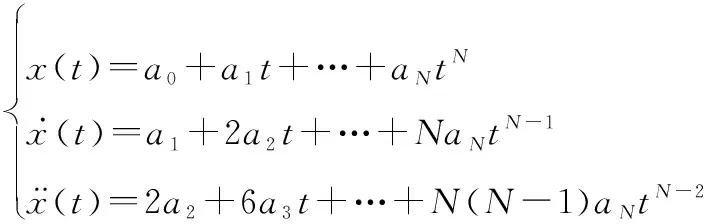
(1)

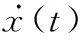
需要注意的是,在实际中状态描述方程组的方程个数需要根据实际的运动状态测量信息确定,如果测量信息只有位置信息,那么只保留式(1)中第一个运动描述方程来描述运动,如果测量信息不止有位置、速度、加速度还有加加速度等,那么就需要增加方程来描述加加速度,其增加规则是逐级求导数。为了方便本文进行算法阐述,本文假设测量信息有3种,分别是位置、速度和加速度。

从式(1)中可以看出,描述运动状态的权系数共有+1个。当=0时位置是常数,描述的是静止的运动状态;当=1时速度是常数,加速度为0,描述的是匀速的运动状态;当=2时加速度是常数,描述的是匀变速的运动状态。越大,状态描述方程所能描述的运动状态就越复杂,所能描述的运动状态种类也越多。

实际中测量运动目标得到的都是点迹信息,所以假设时间间隔是,则式(1)离散抽样简化后可得

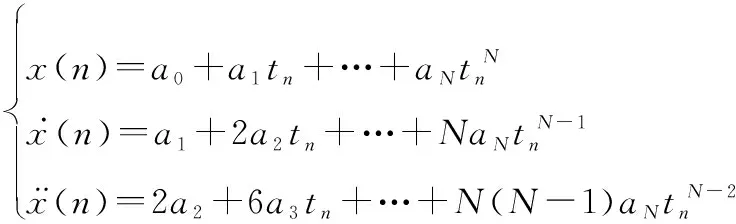
式中:代表时间被时间间隔离散化之后的第个时间点。上式用矩阵的形式表示为

()=

(2)

式中:

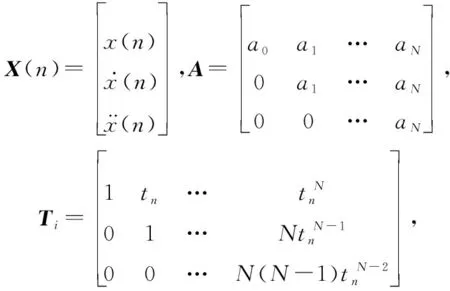
(·)表示矩阵的转置。

2.2 构造误差平方和函数

假设观测到个连续的点迹信息为=[,,…,],其中,,…,为包含了目标位置、速度、加速度等信息的列向量。为了使第21节中提出的运动状态描述方程可以最准确地描述目标的运动状态,则要求观测点和描述点之间的误差达到最小,即和之间的误差达到最小,可以求和之间的最小误差平方和:

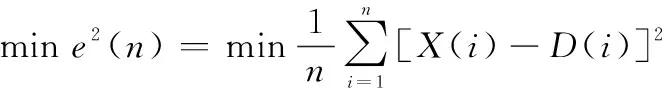
(3)

式中:()代表和之间的误差平方和,min代表取最小。

将式(2)代入式(3)得

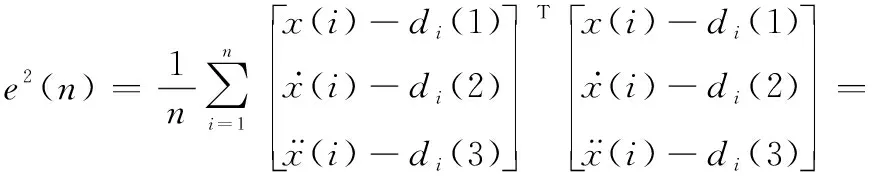
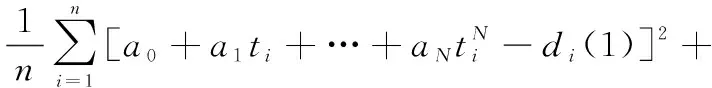
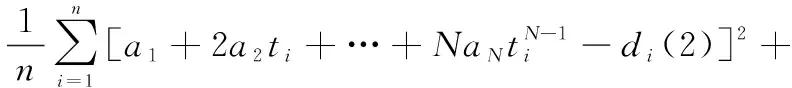
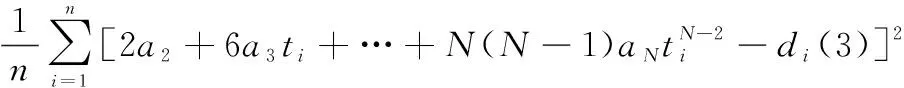
(4)

从式(4)中可以看出,当观测信息给定时,误差平方和函数是一个关于描述运动状态权系数,,…,的函数,应该通过调整权系数使误差平方和函数达到最小,此时权系数所对应的状态描述方程所描述运动状态与目标的实际运动状态最贴近。

但是实际中运动目标的观测信息并不是准确的目标运动状态信息,因为会受到观测噪声的影响。即=+,其中=[,,…,]为目标的实际运动状态,向量(=1,2,…)代表了目标运动的位置、速度、加速度等状态信息。=(,,…,)代表了观测噪声。目标的运动状态相对于噪声是光滑的,由于受到噪声的影响,曲线会出现上下波动的情况,如图2所示。

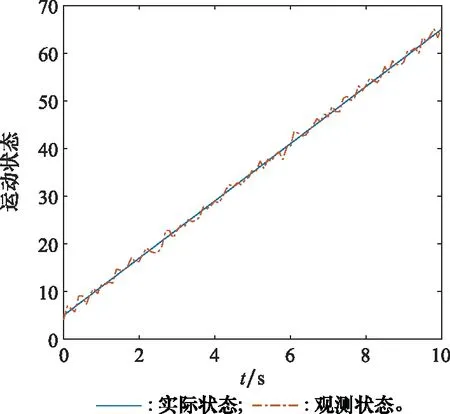
图2 观测状态与实际状态对比图Fig.2 Comparison diagram of observed and actual conditions

由图2可以看出观测运动状态由于观测噪声的影响与实际运动状态相比会变得不光滑,出现波动。如果用描述方程来描述观测运动状态,则相对于实际运动状态会出现过拟合的现象,即描述出来的运动状态也会出现上下波动,所以应该使描述出来的运动状态尽量平滑,避免过拟合现象的出现,以此来过滤掉噪声的影响,对此可以采用正则化的思想。

正则化的思想就是通过引入正则项,使曲线光滑化,防止过拟合现象的发生。引入正则项后的误差平方和函数为

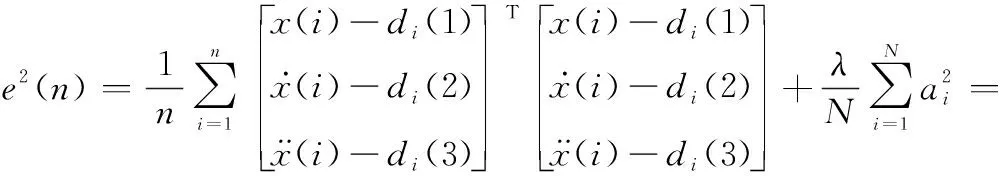
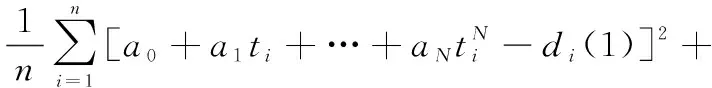
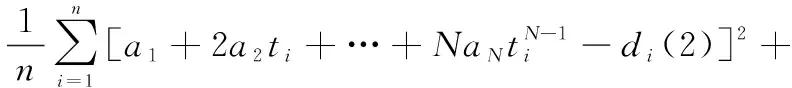
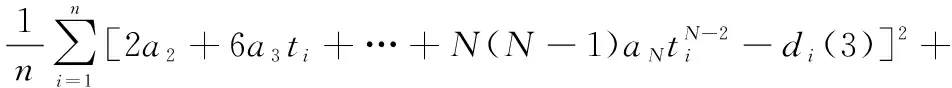
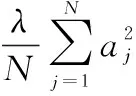
(5)

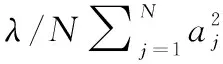
2.3 新最速下降法求最优权系数

新最速下降法是一种采用迭代的方式,逐步求解非线性函数最优值的算法,具有运算量小、实现简单、精度高、鲁棒性强等优点。

将新最速下降算法用于求第22节中所构建的最小误差平方和函数,会得到最优权系数,,…,，由于新最速下降法具有精度高、收敛快、简单等优点,会使对目标的跟踪速度更快、精度也更高。

该方法主要把高维函数降到二维,用抛物线的性质求解极值,利用循环迭代的方式最终求解出使函数达到极值的最优解。

详细推导如下:设有一个维非线性二次函数

(,,…,)=++…+

式中:

=(++…+1+)=(++…+2+) ⋮=(1+2+…++)

,,…,为函数的自变量;为自变量的个数;(=1,2,…,;=1,2,…,)为函数里的系数;代表约束方程的数量。

首先给自变量,,…,随机设置一个初值,,…,,此时函数会变成一个以为自变量,(,,…,)为因变量的二维抛物线,根据抛物线的性质求抛物线的极值点,将此极值点作为。然后将,,…,代入函数,则函数变成一个以为自变量,(,,,…,)为因变量的二维抛物线,根据抛物线的性质求抛物线的极值点,将此极值点作为。如此一直迭代求解,直到求解出之后,重新返回,将,,…,代入函数,求解。如此一直迭代循环求解,(),(),…,()(=1,2,…)随着循环次数的递增将越来越逼近于维非线性二次函数的极值。

抛物线的性质为:抛物线的一般形式为=++,则其极值点位于=-2处。

由上述抛物线的性质知,极值点与抛物线的系数,有关,为了方便求出系数,，可以采用求导数的方式实现。=′(=0),′(=0)代表对求一阶导数,然后令=0。2=″,″表示对求二阶导数。那么极值点为=-′(=0)″。

所以可以推导出维非线性二次函数的求解极值:

(6)

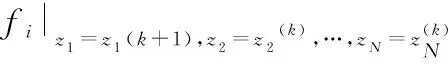
为了使方程可以描述机动目标即运动状态变化频繁的目标,可以求取当前时刻到前-1时刻的个观测点迹的最小误差平方和,得到最佳的运动状态描述方程,以此方程实现对下一时刻目标运动状态的预测。

因为目标预测需要具有实时性,所以的取值应该避免取值过大,经仿真实验得到取3、2甚至是1时都会取得不错的效果。

根据上述所说建立点的误差平方和函数：

()=

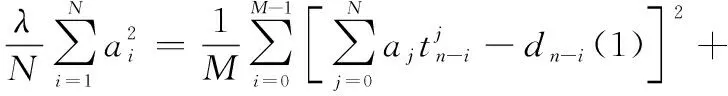
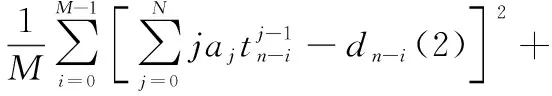
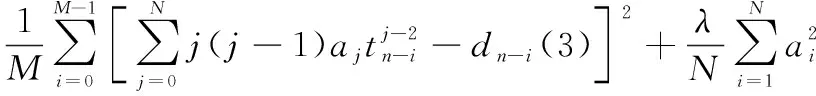
(7)

应用新最速下降法求解点的最小误差平方和,即结合式(6)和式(7)得到描述方程的权系数迭代公式:

⋮

⋮

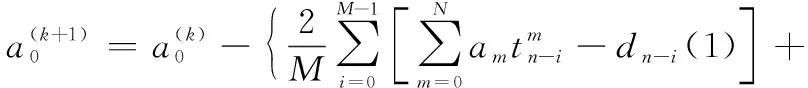
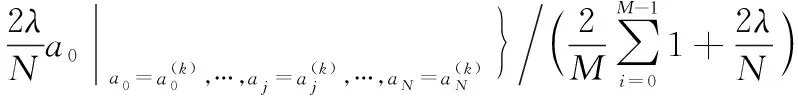
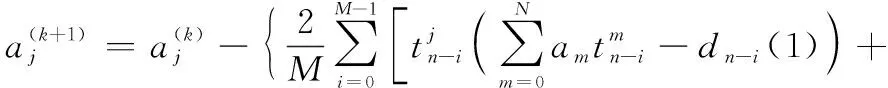
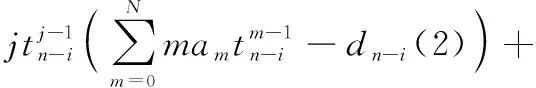
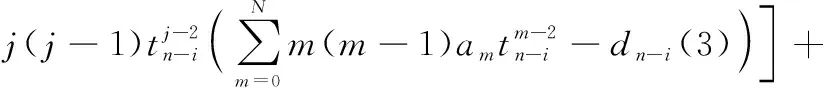
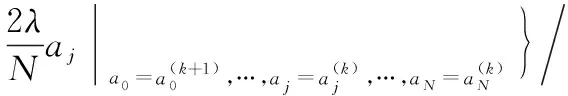
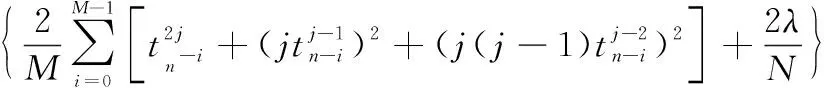
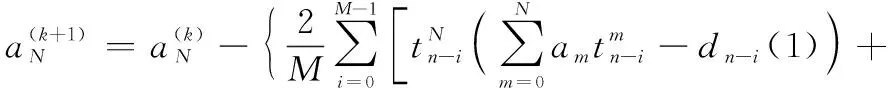
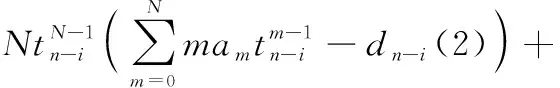
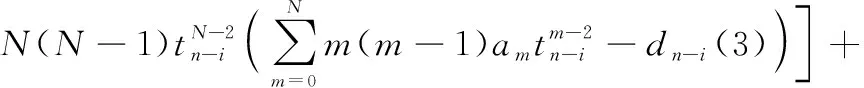
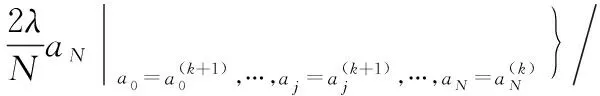
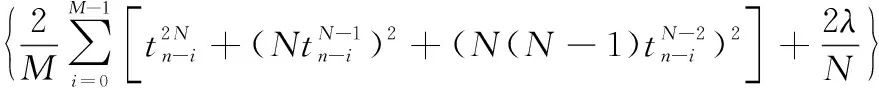
(8)

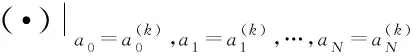
基于新最速下降法的目标跟踪算法应用步骤可以概括如下:

根据观察点迹信息设置描述方程的个数,设置训练点迹数目,设置权系数的个数+1,设置正则化参数;

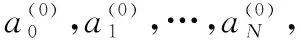
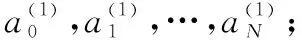
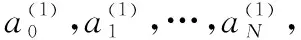
输入新的观测点,对式(7)和式(8)中的-和-进行更新;

重复循环步骤3～步骤5,将步骤4步中目标预测的结果输出。

该目标跟踪算法的基本过程如图3所示。

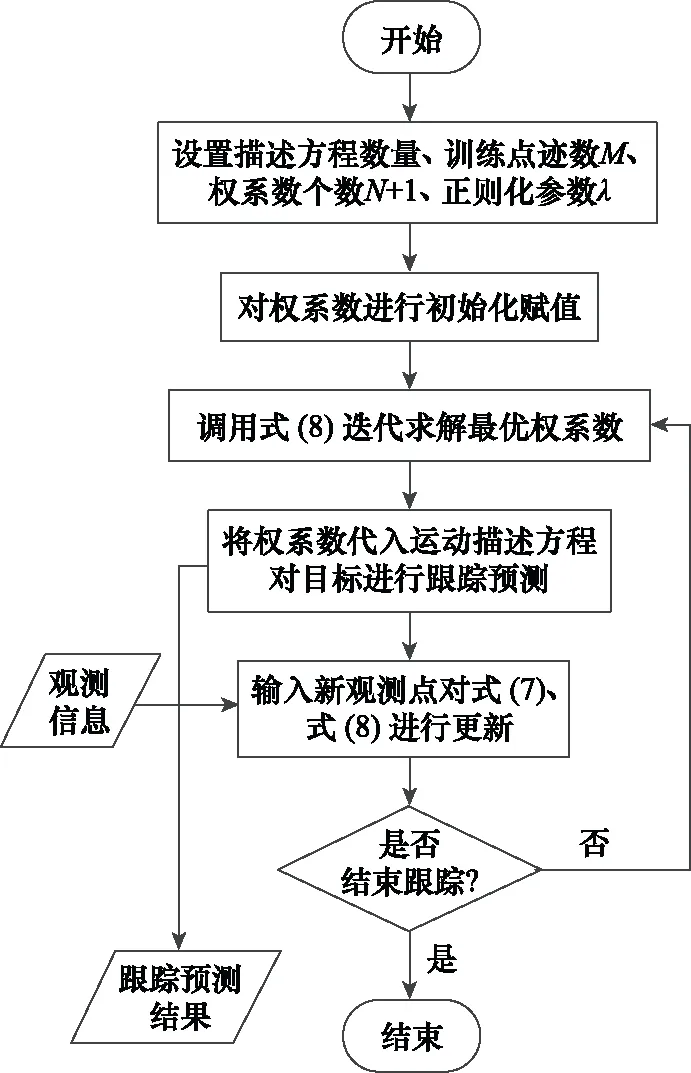
图3 算法过程图Fig.3 Algorithm process diagram

3 仿真验证

3.1 仿真背景

假设目标在二维平面上做平面运动,沿方向做速度为500 m/s的匀速运动,沿方向做机动过载分别为30和26的蛇形机动,表示重力加速度，=10 m/s。两个方向的观测噪声是标准差均为10 m 的高斯白噪声。对运动目标进行测量的采样频率为10 Hz,仿真的时长为10 s。方向的初始位置为80 m,方向初始位置为0 m。得到两个方向的运动方程分别为

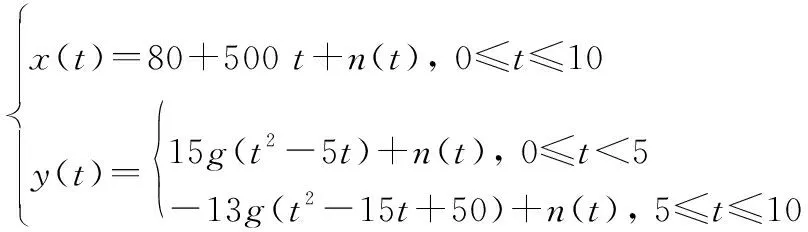
(9)

式中:()～N(0,100)。

IMM里包含两个模型，分别是CV模型和CS模型,CV模型主要针对方向目标做匀速运动,CS模型主要针对方向目标做蛇形机动。初始化马尔可夫转移概率矩阵设为

新算法的模型阶数分别设置为1、2,误差平方和函数所用的点数设置为2。运动模型权系数的初始化赋值为0,以频率10 Hz 即跟踪时间间隔为01 s,对时长为10 s 的运动轨迹进行观测,运动轨迹如式(10)所示,得到101组观测数据。将观测数据和初始化赋值后的运动模型权系数代入式(8)中进行迭代计算得到更新后的运动模型权系数,将计算所得运动模型权系数代入所提出的运动模型，即式(1)，计算出运动目标的预测轨迹,并计算预测值与实际值之间的误差。

用Matlab软件在相同的条件下对新算法和IMM算法进行500次Monte-Carlo仿真,求500次Monte-Carlo仿真的均方根误差(root mean square error, RMSE)。计算公式如下:

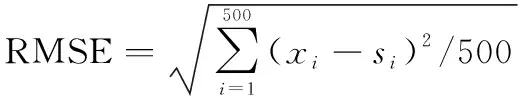
(10)

式中:RMSE表示500次仿真的均方根误差;和分别代表第次仿真的预测状态和实际状态。

3.2 预测轨迹

在第31节的仿真条件下,应用新算法和IMM算法分别对和两个方向抽样所得到的点迹信息进行滤波和预测。然后对得到的两个方向的运动信息进行合成,得到运动目标在平面的预测轨迹。

将两种算法所得到的预测轨迹与目标的实际运动轨迹进行对比,得到的仿真结果如图4所示。

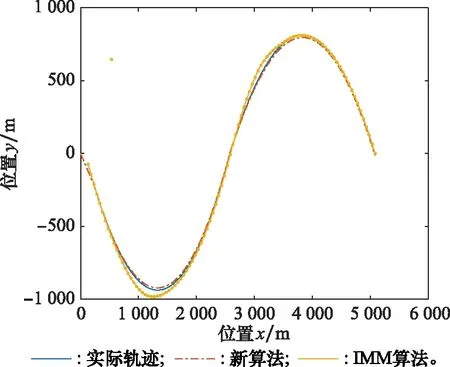
图4 预测轨迹对比Fig.4 Predicted trajectory comparison

从图4可直观地看出,新算法预测得到的轨迹相对于IMM更加贴近目标实际轨迹,对目标的预测跟踪能力更好。

3.3 预测状态与实际状态之间的RMSE

将两种算法预测所得到方向的目标运动状态与实际的运动状态进行对比,计算两种算法预测得到的位置、速度和加速度与运动目标实际的3种运动状态之间的RMSE,得到的结果如图5所示。

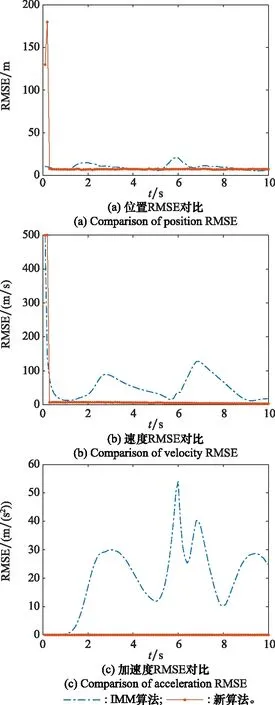
图5 x方向RMSE对比Fig.5 Comparison of RMSE in x direction

从图5中可以看到两种算法一开始对于位置的预测误差基本相同,新算法具有优势。在第2 s和第6 s时,IMM算法对目标位置和速度的预测出现较大的误差,可以从图4中看出,在这两个时间目标突然进行高机动运动,导致运动状态发生很大的变化,因此误差增大。由于IMM算法是多模型交互工作,所以运动状态发生很大变化时,IMM算法需要进行不同运动模型的交互,经过一段过渡时间的调整之后RMSE趋于收敛。求位置RMSE的平均值对两种算法进行对比,经平均计算后得到IMM算法的预测误差的平均值为9.66 m,新算法的预测误差的平均值为7.15 m,所以新算法对于位置的预测更准确。对于速度的预测误差始终是新算法要小一些。综上,新算法对于匀速运动的预测效果相对于IMM算法要更好一些。

将两种算法预测所得到方向的目标的运动状态与实际的运动状态进行对比,计算两种算法预测得到的位置、速度和加速度与运动目标实际的3种运动状态之间的RMSE,得到的结果如图6所示。

图6 y方向均方根误差对比Fig.6 Comparison of RMSE in y direction

从图6中可以看出对于位置的预测,新算法的误差始终较小,IMM算法在目标进行转弯时预测误差会变大。在第2 s和第6 s时,误差突然增大,这也是由于在这两个时间目标进行高机动运动,运动状态的突然变化导致的。此时IMM算法进行模型交互,经过一段过渡时间的调整之后,RMSE重新收敛。对于位置的均方根误差取平均值得IMM算法的位置RMSE预测平均值为20.46 m,新算法的位置RMSE的平均值为14.44 m,所以新算法对位置的预测误差更小。对于速度的预测也是新算法的预测误差更低。对于加速度的预测两种算法各有优劣,新算法预测误差的收敛速度较快,而IMM算法的初始预测误差更低。综上,新算法对于机动目标的位置预测要好于IMM算法,对于速度和加速度的预测则各有优劣。

3.4 运算时间

对两种算法在相同的仿真背景下的运算时间进行计算。运算时间的计算采用Matlab函数对新算法和IMM算法两个程序的运行时间分别进行计时得到。电脑的CPU型号为Intel Core i5-4288U,运行内存为ddr3 12GB,操作系统为Windows7,所安装的Matlab软件为MatlabR2017a。对两种算法500次Monte-Carlo的运行时间进行计时得到:新算法500次Monte-Carlo仿真花费的运算时间是19.297 2 s,IMM算法500次Monte-Carlo花费的运算时间是72.972 0 s。所以新算法的计算量要小于IMM算法,因此新算法更适用于对实时性要求较高的雷达目标跟踪系统。

3.5 新算法与最小均方误差算法对比

图7所示为新算法与最小均方误差(least mean square error, LMSE)算法的性能对比。仿真环境设置为:目标函数是一个6维凸函数,LMS算法的迭代步长设置为0.000 1,经过多次选择得到迭代步长0.000 1,是能使算法收敛的最大迭代步长,初始值均设置为10。从图7中可以看出新算法相对于传统的LMSE算法无论是收敛速度还是计算精度均有较大的优势,新算法的性能要优于传统最速下降法。

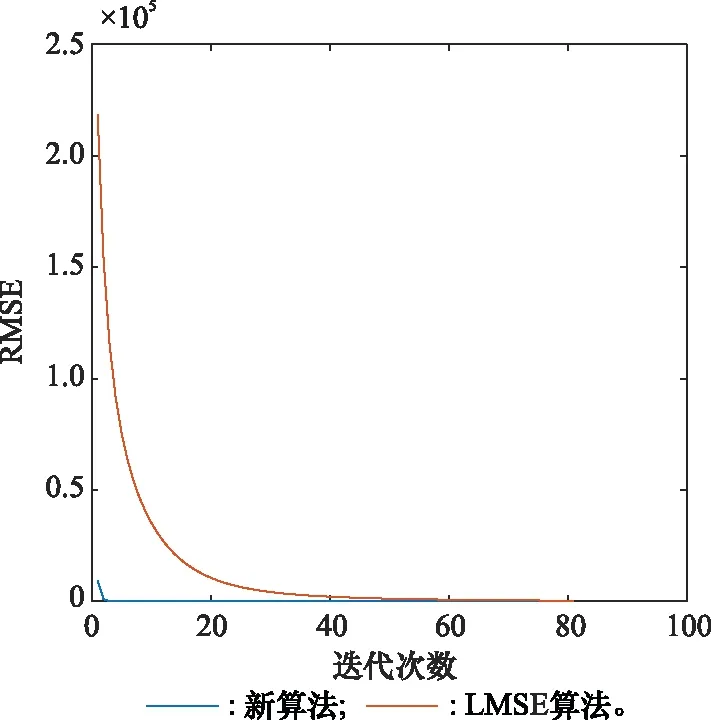
图7 新算法与LMSE算法对比Fig.7 Comparison between new algorithm and LMSE algorithm

4 结 论

本文首先提出了一种基于改进多项式拟合模型的运动模型，然后使用一种新的最速下降算法来求解运动模型中的权系数，最后利用新最速下降法收敛速度快、精度高、运算简单等优点提高了目标跟踪算法的精度和速度。

经过仿真分析得到新算法主要具有如下优点:可以适用于多种不同的运动类型;对运动目标的跟踪预测效果更好,尤其是对于高机动目标;运算量小、实时性较好;易于工程实现。

但是新算法也存在着一定的缺点,由于新算法主要应用数据拟合的方式来进行预测,而对于运动状态急速变化的目标,应该采用高速的取样速率来保持目标预测的精确性。