失效信息已知时r/n(G)表决系统的剩余寿命预测
刘鸿彬, 赵 骞, 贾 祥,*, 郭 波
(1. 国防科技大学系统工程学院, 湖南 长沙 410073;2. 国防科技大学信息通信学院, 陕西 西安 710106)
0 引 言
可靠性指产品在规定的条件下和规定的时间内,完成规定功能的能力,而剩余寿命作为可靠性评估中的重要指标之一,受到越来越多的学者关注。文献[1]指出,产品剩余寿命是指产品未失效的情况下,从当前时刻到产品失效时刻之间的时间长度。可靠性工程中非常关心在当前未失效情况下,产品还能正常工作多久的问题,这可以指导产品的检测、维修以及更换等活动,便于进行可靠性管理,因而对于产品进行剩余寿命的准确预测具有十分重大的意义。
作为典型系统结构,对表决系统寿命与剩余寿命的研究有着十分重要的意义,目前现有文献对于这一问题也开展了相关研究。从函数性质出发,文献[2]对表决系统平均剩余寿命函数性质进行了研究。而基于贝叶斯理论,文献[3]在基于贝叶斯理论的卫星平台剩余寿命预测方法研究中,假定部件服从不同寿命分布,推导中取的表决系统可靠度的封闭表达式;文献[4]对(G)表决系统可靠性进行研究,给出了(G)表决系统的可靠度和平均寿命贝叶斯点估计表达式。在次序统计量相关研究中,文献[5]在对有单个冷备部件的(G)表决系统平均寿命研究过程中,得到了3种不同的平均剩余寿命分布对应使用顺序统计分布的函数;文献[6]通过分析独立同分布下的(G)表决系统的寿命与次序统计量及二项分布之间的关系,给出了(G)表决系统寿命和剩余寿命以及其系统停止工作的时间随总工作元件数量和所需工作元件数量改变的随机序关系;文献[7]在系统层面研究了在当前时刻所有部件都能正常工作的条件下,表决系统平均剩余寿命与顺序统计量之间的关系。文献[8]和文献[9]讨论了表决系统平均剩余寿命的上限;文献[10]和文献[11]研究了部件不完全独立时的相关性质。但不难发现,针对(G)表决系统中部件寿命服从指数分布和威布尔分布等较为常见的分布这类问题,研究已经较为成熟,而对部件寿命服从更一般的分布如指数-威布尔分布的研究较少,剩余寿命预测较为困难。
现有文献中对于指数-威布尔分布下产品的可靠性也开展了研究。针对函数数学性质的研究,文献[12]和文献[13]对指数-威布尔的性质做了更详细的讨论;文献[14]和文献[15]讨论了广义指数分布的相关性质,指出了Gamma分布、威布尔分布和广义指数分布之间的关系;文献[16]和文献[17]研究了指数-威布尔分布的阶原点矩;文献[18]对指数-威布尔分布函数进行了深入研究,通过解析和数值模拟得到了不同参数下指数-威布尔分布相关参数的逆矩阵估计、极大似然估计和Bayes估计。而对于指数-威布尔分布应用于可靠性模型的研究,文献[19]通过串联近似模型给出了指数-威布尔更新函数的近似计算方法;文献[20]在研究组合统计模型的过程中,提出了截断指数-威布尔-帕累托组合模型,模拟了左删失数据的拟合过程,并指出如果在一个平行系统里的个部件的寿命都服从相互独立的指数-威布尔分布,那么这个系统的寿命最终也服从指数-威布尔分布,表明了指数-威布尔分布有很好的物理意义;文献[21]对基于指数-威布尔分布的复杂电子系统展开了讨论,提出了能动态描述系统升级、单元替换、故障维修活动的可靠度模型;文献[22]将指数威布尔分布的失效率函数与两参数威布尔分布以及伽玛分布下的失效率函数进行了对比;文献[23]用指数威布尔分布来模拟真实的生命周期数据得到了应力强度模型的可靠性;文献[24]从指数-威布尔寿命分布出发,研究了个记录值的单阶矩和积阶矩的递推关系和故障率分布的表征;文献[25]研究了广义指数-威布尔分布在实际应用中的通用性,并采用不同的方法对模型参数进行估计;文献[26]推导了广义指数-威布尔分布的统计性质,并用极大似然法估计了分布参数,并观察了分布的渐近性。总体来说,现有的相关研究相对较少,不够深入,特别是如何对部件寿命服从指数-威布尔分布时的表决系统进行剩余寿命预测,目前还未有相关研究。
针对以上问题,本文对部件寿命服从指数-威布尔分布时表决系统的剩余寿命预测方法展开研究。考虑到在实际情况下,若能清楚地得知系统内部件的失效情况,可以大大提升剩余寿命的预测准确度,因而本文具体地探讨了部件失效信息已知时的系统剩余寿命预测方法,并进行了仿真实验和示例验证。
1 r/n(G)表决系统和指数-威布尔分布
(G)表决系统是可靠性研究中较为重要的系统之一,与串联、并联等简单典型系统相比,其结构和工作特性也相对复杂。(G)表决系统由个部件组成,至少有个部件正常工作才可以保证系统正常运行,可靠性框图如图1所示。当个部件独立同分布时,设其可靠度为(),且各部件之间互相独立,则(G)表决系统的可靠度()可以表示为

(1)
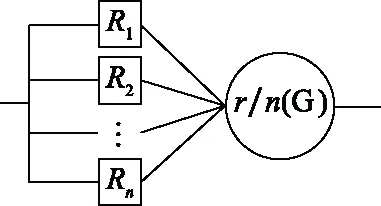
图1 r/n(G)表决系统可靠性框图Fig.1 r-out-of-n: G systems reliability block diagram
指数-威布尔分布是威布尔分布的推广形式,其形式相对其他分布比较复杂,包含4个参数。设随机变量服从指数-威布尔分布,其相应的累积分布函数(cumulative distribution function, CDF)如下:
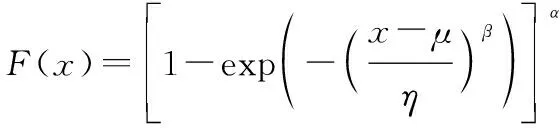
(2)
式中:为位置参数;为第一个形状参数;为第二个形状参数;为尺度参数,相应的概率密度函数为
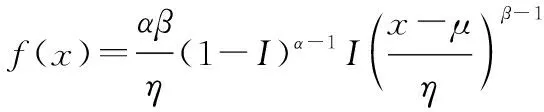
(3)
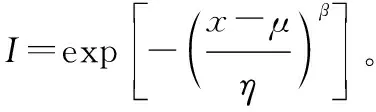
失效率函数为
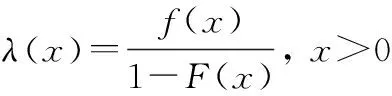
(4)
当位置参数=0时,该分布简化为三参数指数-威布尔分布。相比起指数分布和威布尔分布一般只能对失效率为常数或单调的情况进行建模来说,其优势在于可以对失效率不单调的情况进行建模,即能对单峰、浴盆或反浴盆等情况进行建模。图2展示了分布参数不同取值下的失效率函数曲线。
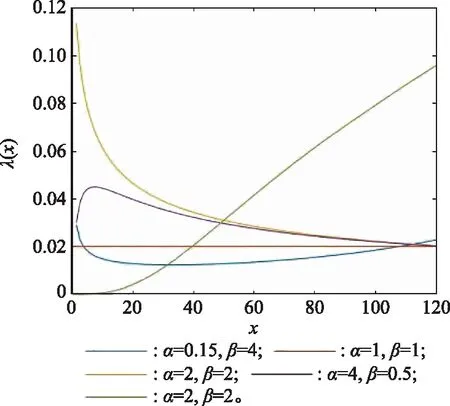
图2 失效率函数曲线Fig.2 Failure rate function curve
文献[27]将指数-威布尔分布下的失效率函数曲线的特征总结如下:
(1) 当==1,失效率函数值为常数;
(2) 当>1且<1,曲线为浴盆形状;
(3) 当<1且>1,曲线为反浴盆、单峰形状;
(4)≥1且≥1(≤1且≤1),曲线为单调函数。
2 模型假设
相比于复杂的四参数指数-威布尔分布,三参数指数-威布尔分布的实际应用层面更广。本文进一步假定部件寿命服从三参数指数-威布尔寿命分布,相应的失效分布函数如下:
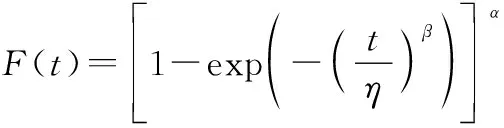
(5)
概率密度函数为
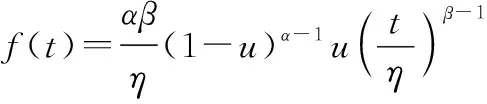
(6)
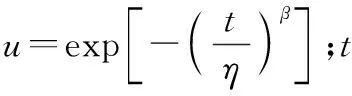
假设为部件工作时间,()为部件失效分布函数。部件失效分布函数可表示为
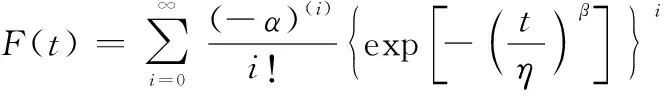
引入广义二项展开式:
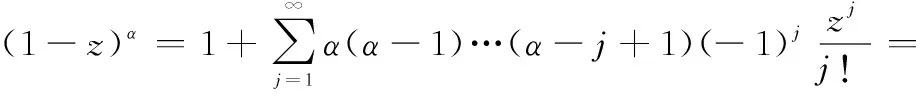

式中:()()=(+1)…(+-1)为上升阶乘幂,()=1,可得
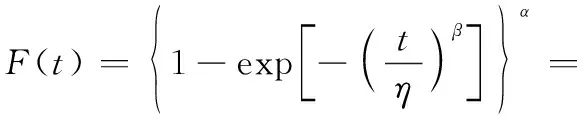
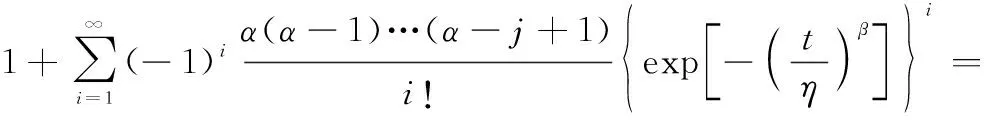
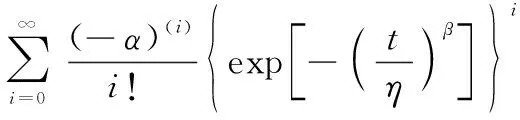
证毕
特别地,当≥1且为整数时,上式可以写为

(7)
假设为部件工作时间,()为部件失效分布函数。记为(G)表决系统中失效部件个数,则为时的概率为
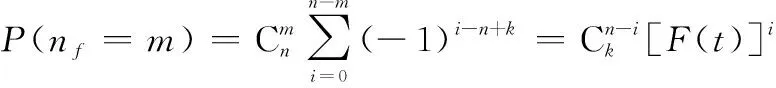
由二项展开得


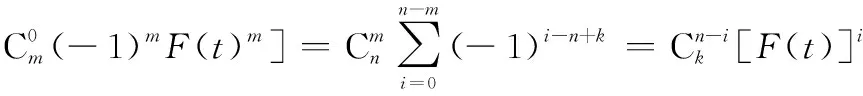
证毕
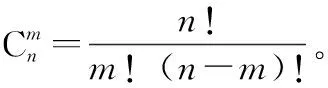
结合定理1,进一步可得
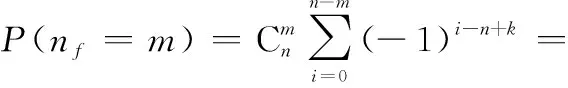
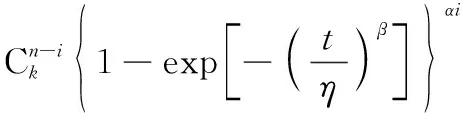
(8)
定理1给出了部件失效分布函数的另一种数学形式,便于后续的积分运算;定理2给出了失效信息已知时,失效若干部件的条件概率,便于后续计算(G)表决系统的可靠度函数()。
3 失效信息已知时表决系统的剩余寿命预测
本节假定部件寿命服从式(5)形式的指数-威布尔分布,对表决系统的剩余寿命进行预测。
文献[28]在研究可靠度与剩余寿命的关系中,给出了如下定理:
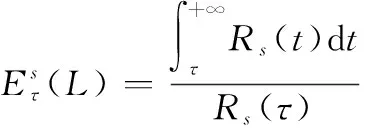
(9)
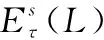
另外在实际工程中,常常可以获得系统的失效信息,如当前时刻表决系统中失效部件的个数。从信息论的角度,为了对剩余寿命进行准确预测,需要充分利用这些信息,如果对失效信息忽视,往往造成剩余寿命预测结果不够准确。但目前面临的一个困难是,在已经知道失效信息的前提下,如何利用这些信息对系统进行剩余寿命的准确预测。
3.1 失效信息已知时r/n(G)表决系统的剩余寿命
先考虑部件失效信息已知时的表决系统剩余寿命。根据式(9)可知,若要通过解析推导得到失效信息已知情况下(G)表决系统剩余寿命点估计和区间估计解析表达式,首先需求得失效信息已知时的(G)表决系统可靠度()。
已知失效个部件时,(G)表决系统的可靠度函数需要通过条件概率计算。这里设失效部件数量为,系统已工作时间为,此时可靠度()可表示为
()=(>|=)=
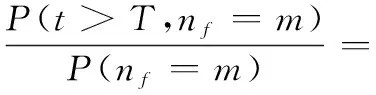
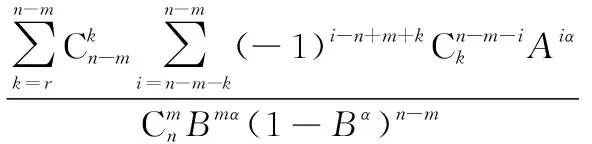
(10)
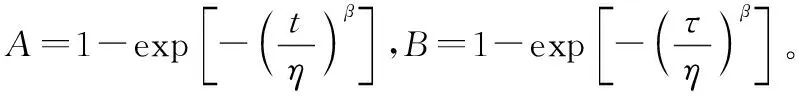
已知失效个部件时,系统工作时间为,将式(10)代入式(9)可以推导得时刻(G)表决系统剩余寿命点估计表达式为
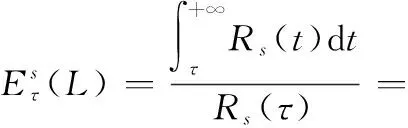
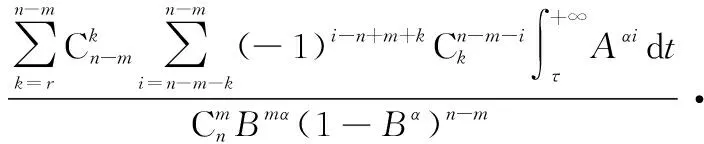
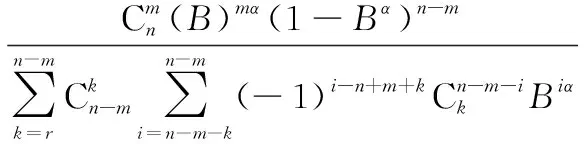
(11)
对式(11)进行简化可得
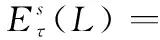
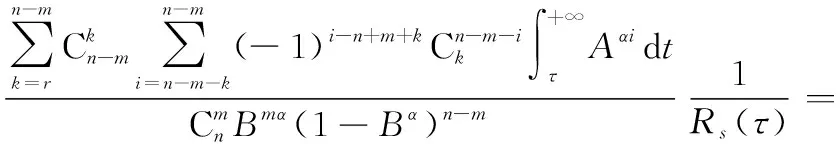
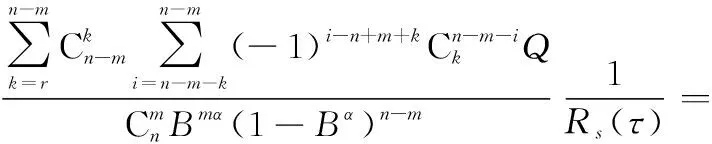
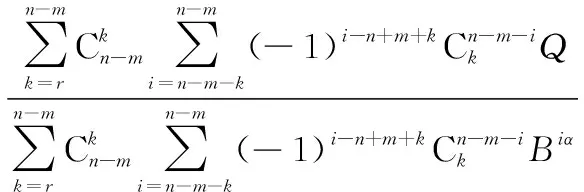
(12)
式中:
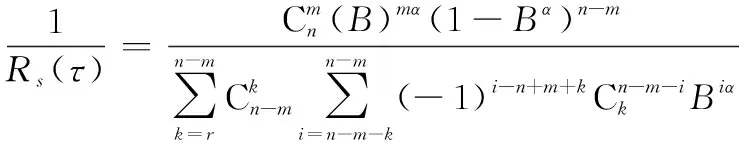

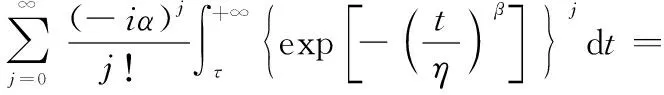
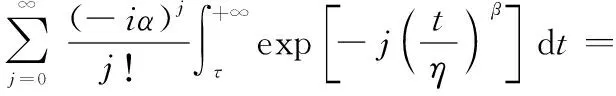
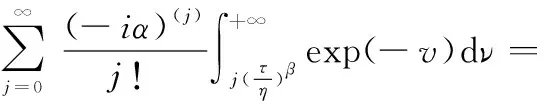

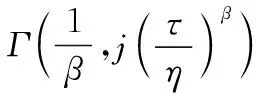
假设置信水平100(1-)%下剩余寿命的置信区间为[,],则有
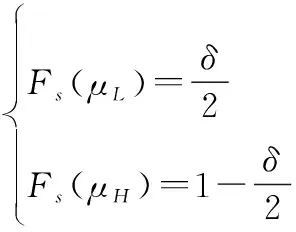
(13)
其中,表决系统剩余寿命失效分布函数为
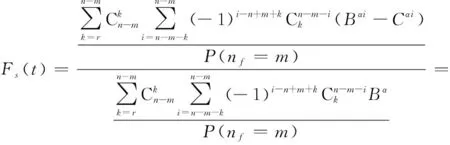
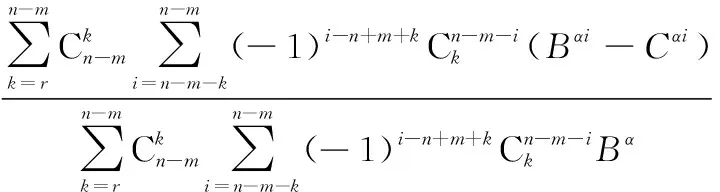
(14)
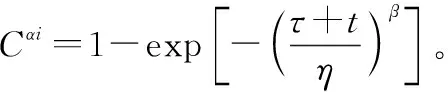
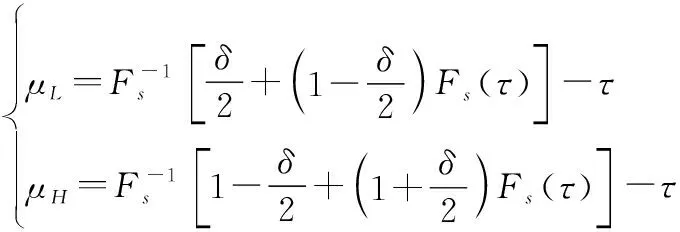
(15)
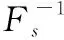
3.2 部件寿命服从威布尔分布情况下的剩余寿命估计
威布尔分布作为指数-威布尔分布的特殊形式,此处再考虑部件寿命服从威布尔分布下的剩余寿命。若部件寿命服从威布尔分布,已知失效个部件时,系统已工作时间为,可以得到(G)表决系统可靠度为
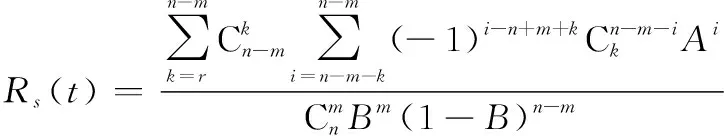
(16)
其剩余寿命点估计表达式为
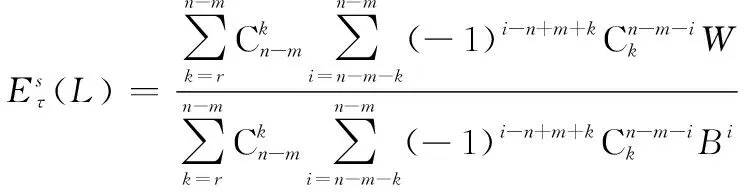
(17)
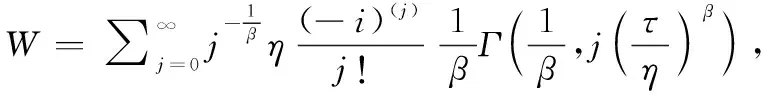
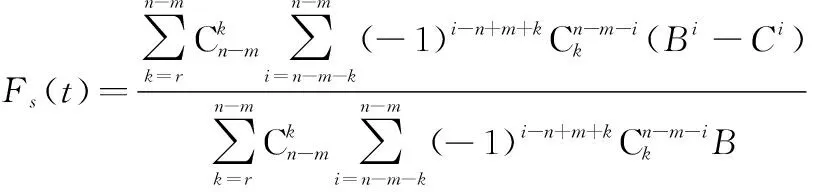
(18)
相关计算方法参见第21节。
3.3 部件失效信息未知时的剩余寿命估计
当部件失效信息未知时,(G)表决系统的可靠性函数()可表示为
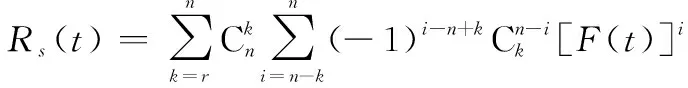
(19)
系统已工作时间为,部件寿命服从指数-威布尔分布时,(G)表决系统剩余寿命点估计表达式为
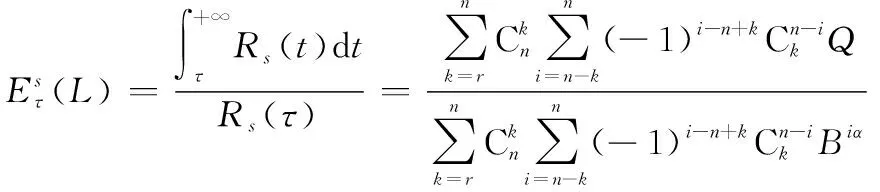
(20)
同样给定100(1-)%置信水平下剩余寿命的置信区间为[,]满足式(13),此时(G)表决系统剩余寿命失效分布函数为
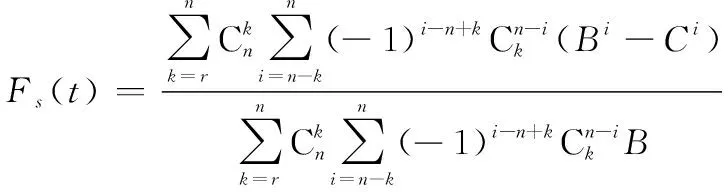
(21)
相关计算方法参见第21节。
4 方法验证
本节通过蒙特卡罗仿真实验来验证本文提出的失效信息已知情况下部件寿命服从指数-威布尔分布时(G)表决系统的剩余寿命预测方法的准确性和有效性。
4.1 试验过程
为了验证推导,首先给出表决系统寿命的仿真方法。假设(=1,2,…,)表示为(G)表决系统中部件(=1,2,…,)的寿命,且各之间相互独立互不影响,表示(G)表决系统寿命。通过对部件的寿命进行升序排列,得到一组数据≤≤…≤,则根据(G)表决系统的结构特性,可以定义其寿命为=-+1。在此基础上,进一步分析表决系统剩余寿命的仿真方法。基于上述讨论,给出仿真实验的步骤,验证所提方法的有效性。实验过程如图3所示,具体步骤如下。
给定系统的失效部件数,系统已经工作的时间;设(G)表决系统剩余寿命样本的抽样次数为,部件总数为,在工作的部件数为,令=1,=0;
从=1开始,根据(G)表决系统中部件给定的指数-威布尔参数(,,),采用逆函数法在0~1之间随机取均匀的若干个概率值,随机生成部件的寿命样本。当=时停止;
将寿命样本升序排列,则系统的寿命()=-+1;
从=1开始,判断是否满足()<,满足,则=+1;
若满足()>,则令剩余寿命RL()=()-,否则返回步骤3;
判断(G)表决系统在工作时间后是否损坏且仅损坏个部件,如果不是则返回步骤2;
判断是否满足<,满足,则令=+1,返回(2);不满足,输出(G)表决系统寿命的样本RL(1),RL(2),…,RL();
根据RL样本,完成剩余寿命预测。
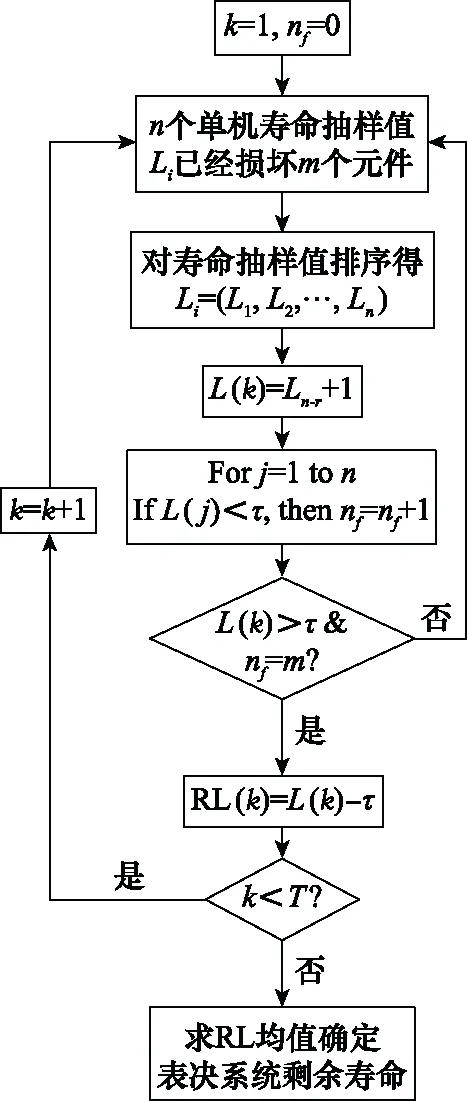
图3 剩余寿命仿真实验流程图Fig.3 Flow chart of residual life simulation experiment
表1给出了4组不同参数下剩余寿命点估计仿真方法和数值计算结果对比,表2给出了与表1同样参数的4组剩余寿命80%置信度下的区间估计数值计算和仿真方法结果对比。
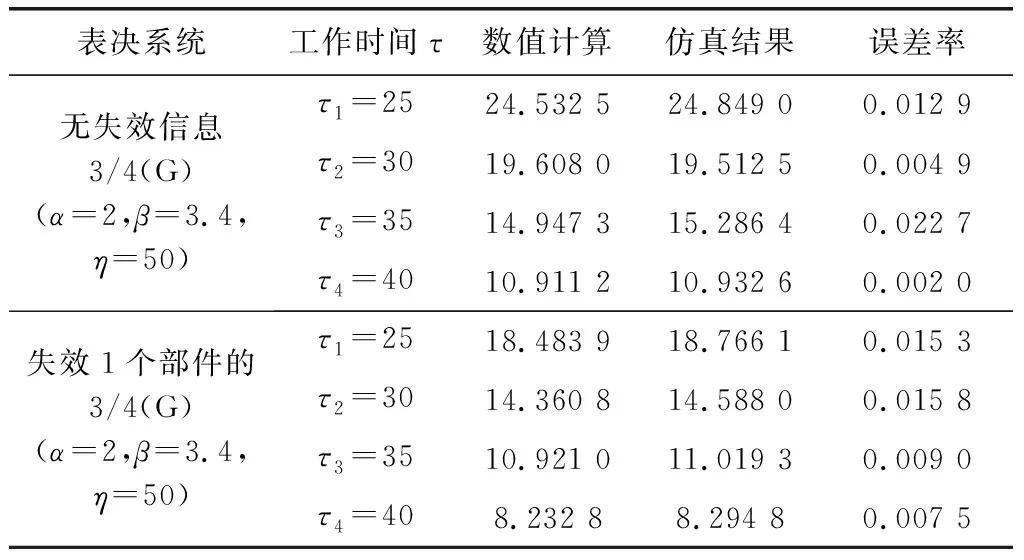
表1 剩余寿命点估计数值计算和仿真方法对比
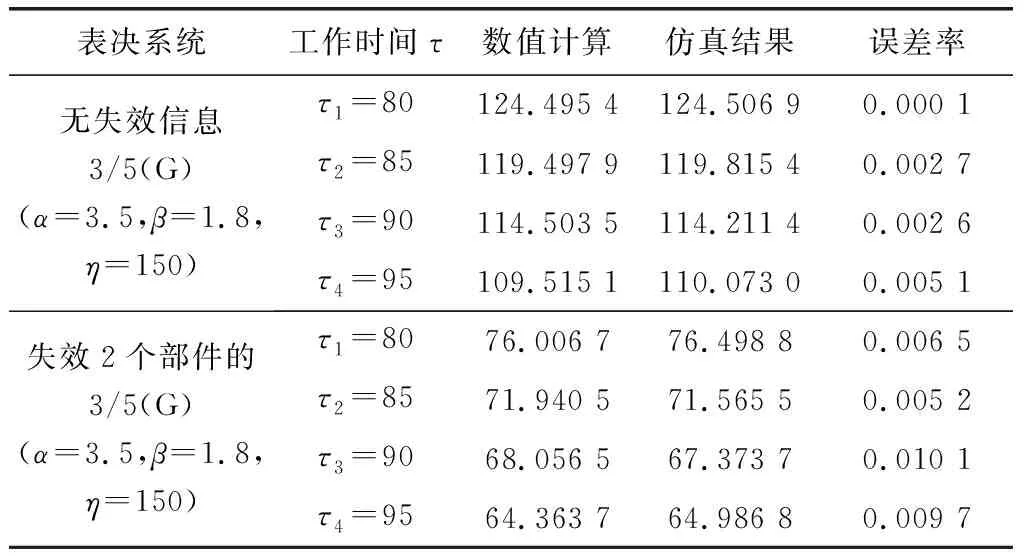
续表1

表2 剩余寿命区间估计数值计算和仿真方法对比
此时在给定参数下仿真方法得到样本的剩余寿命CDF图像如图4所示。
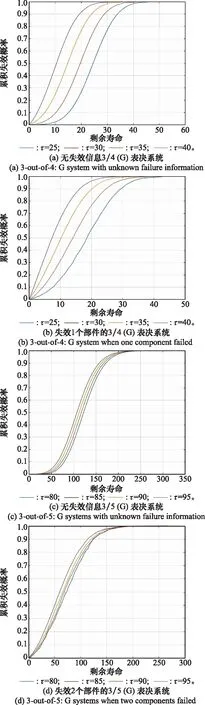
图4 仿真方法得到的剩余寿命CDF函数图像Fig.4 Residual life CDF function image obtained by simulation
4.2 试验结果分析
从表1和表2中的结果分析易知,与仿真结果相比,利用本文提出方法所得的剩余寿命点估计和区间估计,其误差都在合理范围内。因而,本文所提出方法是准确的、有效的。
表1和表2中的结果也表明,当表决系统中存在失效部件,但忽略这些失效信息开展剩余寿命预测所得的结果,与真实情况相比偏差很大。例如,当3/4(G)表决系统工作时间为τ=30时,且存在一个失效部件时,如果按照式(20)中忽略失效信息的方法求得的系统剩余寿命预测结果为19.608,但按照式(11)中利用失效信息的方法所得的结果为14.360 8。显然,存在失效信息但在预测系统剩余寿命时未对其进行充分利用,对预测结果将会产生显著影响。这也说明了本文研究的必要性。
5 示 例
本节通过两组不同示例来说明本文所提出剩余寿命预测方法的具体应用,证明该方法在工程实践中的有效性。
5.1 示例1
本示例采用文献[29]给出的公开数据来说明本文所提出的方法的具体应用。表3给出了50台设备的失效时间数据。总失效时间图像显示其失效率曲线为浴盆形状。文献[12]在对该数据研究中表明指数模型和威布尔模型是不成立的,然后采用三参数指数-威布尔分布对数据进行拟合。
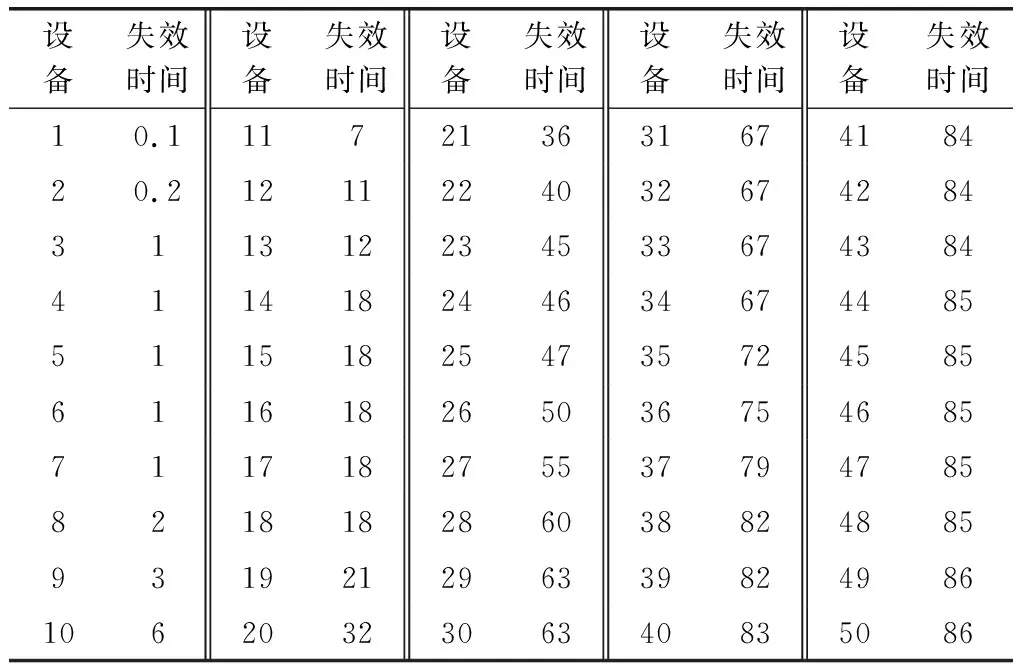
表3 50台设备的失效时间Table 3 Lifetime of 50 devices d
文献[25]对表3给出的数据集进行分析,采用二参数指数-威布尔分布去拟合数据并通过改进后的贝叶斯估计方法计算得到参数的估计值为=635,=022,=1,此时的寿命分布相当于是两参数指数-威布尔分布。
进一步,对于该类设备构成的3/4(G)表决系统,根据设备寿命的分布参数估计值,利用本文所提出的预测方法,若已知该系统失效1个部件,即=1,由式(10)可计算得到在系统已工作时间=50 d,可靠度估计值为()=0.467 9;由式(11)可计算得到该表决系统的剩余寿命点估计值为72.497 7 d;由式(12)~式(14)可计算得到剩余寿命60%置信区间为[10.028 9 d, 101.876 3 d]。此时在给定参数下所得的剩余寿命CDF如图5所示。
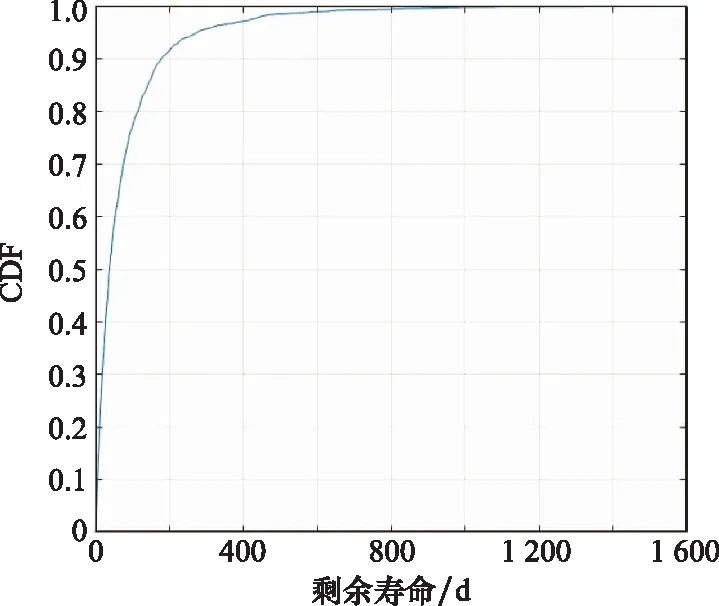
图5 示例1中设备剩余寿命的CDF函数图像Fig.5 CDF function image of device’s residual life in example 1
5.2 示例2
本示例以动量轮为例,说明本文所提出方法的具体应用。动量轮是卫星的关键部件,其可靠性对卫星的可靠性至关重要。
文献[30]对融合两类数据对动量轮的可靠度估计方法进行了研究,给出了现阶段3颗某型号卫星(共有15个具有相同失效机理的动量轮, 截至目前均无失效)在轨运行时间统计如表4所示。
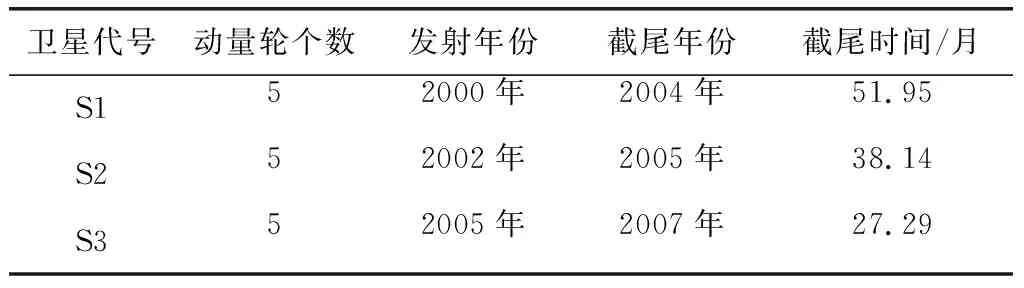
表4 动量轮在轨运行时间
文献[25]给出了卫星动量轮寿命分布的参数估计值为=1,=1670 1,=601276此时寿命分布为威布尔分布, 且在=24月时可靠度估计值为()=0955 4。
进一步,对于卫星动量轮构成的4/5(G)表决系统,此时暂不知道失效信息,根据动量轮寿命的分布参数估计值,利用本文所提出的预测方法,由式(15)可计算得到在系统已工作时间=24月时,该表决系统可靠度估计值为()=0998 1;由式(16)可计算得到该表决系统的剩余寿命点估计值为327.457 9月。由式(17)和式(18)可计算得到剩余寿命50%置信区间为[215.848 1,421.277 5]。此时在给定参数下所得的剩余寿命CDF图像如图6所示。
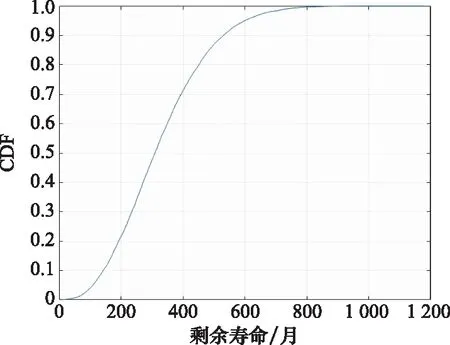
图6 示例2中动量轮剩余寿命的CDF函数图像Fig.6 CDF function image of momentum wheel’s residual life in example 2
6 结 论
在实际可靠性工程中,对部件的寿命以及剩余寿命进行估计尤为重要。现有研究通常假定(G)表决系统中部件寿命服从简单的指数分布或威布尔分布,应用相对有限。本文考虑部件寿命服从指数-威布尔分布这一种通用分布,结合表决系统结构相关特性和规律,在部件失效信息已知时,提出了表决系统的剩余寿命预测方法,并给出了剩余寿命点估计和区间估计的解析式。经过仿真实验的分析,发现所提出的计算方法是高效的、准确的,且表明忽略部件失效信息对系统的剩余寿命进行预测,所得结果偏差很大。最后用两个算例说明了所提出方法的具体应用,证明了该方法在工程实践中的有效性。

