基于NSGA-II的波前相位畸变特性分析

陈嘉贝, 王青平, 叶 源, 吴微微, 袁乃昌

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410000)

0 引 言

多元矢量合成干扰作为一种电子欺骗干扰技术,可以有效地对所有类型的射频跟踪系统产生测角误差,被认为是对抗单脉冲雷达最有效的干扰方式之一[1-2]。而由该方法所产生的误差是因为目标回波的波前相位发生了失真[3-4]。

雷达目标视在角位置的变化也被称为角闪烁效应。1959年,美国海军研究实验室使用高速单脉冲雷达进行了相关实验。实验表明,角闪烁效应是源于复杂目标的各个部分接收到的信号的相对相位的变化[3]。在天线孔径处进行矢量求和时,这些时变相位导致雷达回波的视在到达角的变化,从此,多元矢量合成的干扰方法在电子战领域开始备受关注。

对多元矢量合成的干扰方法的研究中,以交叉眼干扰研究最多,每一个交叉眼干扰环路由两个振幅近似相等相位相反的阵元构成[5]。南非学者Du Plessis等基于被干扰方雷达的测角体制,建立了典型的两元交叉眼干扰模型,并对其进行严苛的数学推导,得出了误差角度的相关表达式[6]。随后,就影响误差角度的相关因素进行了分析,建立了一个从对抗方雷达角度的研究思路[7-8]。由于两元交叉眼干扰方案对系统参数要求过于严苛,一般而言,在相位差偏离π超过5°,干扰效果就很不理想[9-10]。因此,国内学者Liu等在Du Plessis等的研究基础上进一步拓展了干扰环路,建立了多环路交叉眼干扰模型[11-13],提出了一种提高干扰性能的新方案。西安电子科技大学的Liu等考虑平台旋转问题,提出了正交单环路旋转反向交叉眼方案[14],引入稳定因数的概念作为新的评判标准,衡量产生稳定角度干扰的能力,并得出关于角度偏差的闭合解方程。虽然多环路的模型能够一定程度上改善交叉眼干扰性能[14-16],但是也存在环路差异的缺点,包括器件之间的差异[17-18]和干扰路径差等[19-21]。在交叉眼干扰的实践应用上,Pieterse借助软件定义无线电实现了反向交叉眼眼干扰机的测试[22],Kalinbacak在仿真软件中对交叉眼干扰机进行性能测试[23]。

此外,还有学者从干信比的角度分析交叉眼干扰的性能,电子战领域普遍认为20 dB以上的干信比才能使交叉眼干扰产生有效干扰[24-26],但中南大学学者Yang等通过分析交叉眼干扰增益的分布情况,认为干信比需大于30 dB才能使交叉眼干扰系统有稳定的干扰性能[27]。

以上,都是从被干扰雷达角度分析多元矢量合成的干扰效果。而从干扰方研究波形的波前相位问题时,国外学者Harwood将传统交叉眼干扰技术扩展到多个阵元,使干扰系统有更多的自由度控制所需的场方向图[28]。同时可以获得更宽的干扰扇面宽度,从而提高干扰性能,但并未对相关干扰指标进行理论推导。国内学者殷红成等利用严格的电磁散射理论,推导了基于振幅和差式和相位和差式单脉冲雷达测角原理的复杂目标角闪烁的一般表达式,对雷达目标角闪烁的两种物理概念提出了新的解释和认识,揭示出波前畸变概念、能流倾斜概念和雷达角噪声产生原理三者之间的内在关系[29-30]。王国伟等建立了以中心相位畸变程度和有效相位畸变区为目标的约束模型,从波前相位的角度分析了多环路交叉眼干扰的干扰性能[31],但该研究局限于交叉眼干扰,未对任意多元情况进行分析。

本文中,首先建立了多阵元的干扰场景,推导了该场景下空间中任意一点的合成波信号表达式。基于该表达式,以增大误差角度和拓宽干扰扇面为目的,用中心畸变程度和有效畸变区作为性能指标,建立相应的目标优化函数,利用NSGA-II智能优化算法对各个阵元的信号幅度调制参数、相移量等参数进行优化计算,最后仿真出优化后的相位波前分布。

1 数学模型及分析

1.1 多元矢量合成干扰系统

多元矢量合成干扰系统将每一个天线阵元发出的电磁信号视作为一个矢量[31],系统由N个天线阵元构成。目标雷达发射信号,天线阵元对信号进行幅度、相位调制,从而得到N路相干干扰信号,相干信号在空间中互相叠加,对远场中的某一个目标而言,这N路相干干扰信号的传输路径是相同的。但是,由于回波信号进行了调制,因此在雷达接收天线处将产生扭曲的波前,使雷达错误估计从干扰源到接收天线的信号路径的方向,随之而来的是增大了雷达的角度跟踪误差。

1.2 模型分析

多元矢量合成干扰场景如图1所示[11]。在实际场景中,存在更多的排布方式,但是考虑到阵元的排布主要影响的是干扰信号的相位差,且由排阵方式引起的相位差可以很容易计算出来并补偿。所以,简单起见,本文考虑阵元等距离排布的线阵这一场景,且该场景具有通用性。

如图1所示的干扰系统中,该系统由多个阵元构成,若阵元总数为2N+1,则在阵元中心处的阵元编号为0,若为2N,阵元中心则无阵元。y轴正方向的阵元由上至下依次编号为1,2,…,N且阵元间距为da,y轴负方向的阵元由上至下依次编号为N+1,N+2,…,2N且阵元间距为da,天线阵总长为dc。则

da=dc/2N

(1)

干扰中心到目标雷达P点的距离为r0,干扰天线阵元中心到P点的路径与干扰天线正方向的夹角为θ0,阵元i到P点的距离为ri,干扰天线正方向与阵元i到P点的路径夹角为θi。由图2中的几何关系,y轴上侧的阵元与点P的距离为

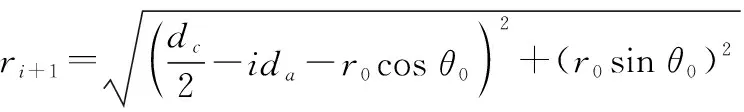
(2)

y轴下侧的阵元与点P的距离为

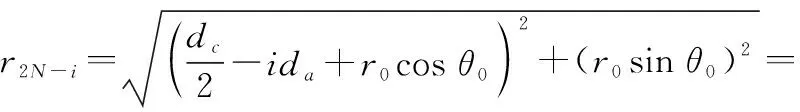
(3)

当P点处于远场的其他位置,也可用相同的方法计算出ri。

假设多元矢量干扰系统中第i个天线阵元发射信号幅度为Ai,相位为φi,则第i个天线阵元发射的信号[14]可以表示为

Ei=Aiej(ω t+φi)

(4)

在远场空间中的某点P处,第i个天线阵元发射的信号到达点P时的信号为

Ei=Aiej(ω t+φi)

(5)

其中,

(6)

ω为信号的角频率,c为光速。

则合成波信号E[32]为

(7)

(8)

式中:

(9)

1.3 波前相位畸变分析

多元矢量合成的波前畸变分析主要依赖于波的相干叠加原理,即频率相同,振动方向相同,相位差恒定的波互为相干波,在空间中任一点的辐射场为各列相干波在该点的辐射场之和,而单脉冲测角误差就是由该辐射场的相位畸变造成的。

相位畸变即在与信号波源相同距离的圆周内相位发生变化,如图2所示,畸变区越大,畸变程度越大,单脉冲雷达测角误差越大[33]。因此,一般用畸变区和畸变程度作为相位畸变的表征。

本文中使用相位的变化率k表征相位畸变程度,即有

(10)

式中:phase(E)表示E的相位。图2所示的场景中,可以认为当天线阵列对准目标雷达时,即θ0=90°时的相位梯度为中心畸变程度k0,即

(11)

多元矢量合成的干扰方法只有在有效畸变区内才能对单脉冲雷达进行有效的干扰,定义有效畸变区ρ为

(12)

kmin是能达到有效干扰时的最小梯度值,此时对应的角度值分别为θh和θl。

根据图2所示的干扰场景,在两个干扰阵元的情况下,假设干扰距离为1 000 m,两阵元信号幅度比为0.95,根据式(12)可得到在干扰中心点附近的不同相位差情况下的合成相位变化情况如图3所示。

从图3可以观察到,由于两个相干信号的合成,导致了合成信号在干扰中心处发生了严重的畸变。当两阵元相位差为180°时,干扰中心畸变程度最大,且在干扰中心左右迅速变化并趋于平缓,而当两阵元相位差为其他值时,合成相位畸变最大点将不在中心位置,但在畸变中心附近的相位变化相较相位差为180°时更急剧。由单脉冲雷达的测角原理可知,雷达是通过对目标回波的幅度和相位分析确定目标位置的。因此,当雷达接收到的信号相位发生畸变,就会对雷达测角产生一定的误差,且畸变程度越大,误差越大。因此,当两阵元相位差为180°时,干扰中心位置干扰效果最佳,但干扰范围却是最小的。

2 最优相位畸变策略

2.1 优化模型

在对单脉冲雷达的角度欺骗研究中,相位畸变程度越大,造成的角度误差越大,有效畸变区越大,干扰对于单脉冲雷达的横向运动越不敏感,干扰效果越好[28]。因此,可以建立优化函数:

(13)

根据文献[31],可以假设kmin为干扰系统与雷达对准时使雷达指示角偏离0.5倍波束宽度达到失锁状态所需的最低中心畸变程度。在这个优化模型中,为了使得畸变程度k0和畸变区域ρ最大,可以优化的参数包括阵元个数、阵元间距以及每个阵元的相位与幅度。

式(13)为一个典型的多目标优化问题,联立式(9),不难发现,影响优化问题的决策变量有阵元的幅度Ai,阵元的相位φi,阵元间距da以及阵元个数。

2.2 优化算法

对于如式(13)所示的多目标优化问题,不存在单个最优的解,只存在最优解集,即Pareto解集,而NSGA-Ⅱ是目前最流行的多目标遗传算法之一,因其降低了非劣排序遗传算法的复杂性,具有运行速度快、解集的收敛性好的优点,成为其他多目标优化算法性能的基准。利用NSGA-II求解式(13)的Pareto解集如下。

步骤 1初始化算法参数,生成大小为N的初代种群Pop,即随机生成N组解集;

步骤 2基于非支配排序对种群进行排序,并为每个个体分配等级;

步骤 3执行选择、交叉、变异操作,从初代种群Popi中生成子代种群Oi;

步骤 4执行合并操作,将父代种群Popi和子代种群放在一个缓冲池中,并基于非支配排序进行排序;

步骤 5从最优排名F1,F2,F3,…中选出非支配解组成下一代种群Popi+1,直到放入某个Fn时,Popi+1的大小超过N;

步骤 6根据拥挤度距离排序,从Fn中选择个体使Popi+1的大小等于N;

步骤 7判断算法运行终止条件,若未达到最大迭代代数Gen,则转去执行步骤2,否则终止算法并输出最优解。

在上述求解过程中,对种群排序主要是基于非支配排序,这一排序过程具体如算法1所示。

算法 1 非支配排序算法1: for each p∈Pop2: for each q∈Pop3: if (p支配q) then4: q加入p支配的解的集合Sp5: else if (q支配p) then6: p的被支配个数np++7: if (np=0) then8: 将p加入第1层非支配集合F19: i=110: while (Fi≠⌀) do11: H=⌀12: for each p∈Fi13: for each q∈Sp14: nq=nq-115: if (nq=0) then16: H=H∪p17: end while18: i=i+119: Fi=H

3 实验与分析

实际场景中,影响干扰效果的因素有很多,其中包括天线阵元的个数、天线阵元的间距、雷达频率、天线波束宽度等。不失一般性,本文对一些重要参数做如表1所示的设定[20]。

表1 实验参数设置

接下来,以各个阵元的相移,幅度调制比例为变量,各个阵元的相移变化区间为[0°,210°],幅度调制的变化区间为[0,1.05],以有效畸变区间和中心畸变程度为目标函数,基于NSGA-II算法求解目标函数的最优Pareto解。其中,NSGA-II算法中种群大小为200,最大迭代次数为400,适应度函数偏差为10-10。

如图4所示,分别是不同阵元合成情况下的Pareto解集分布,Pareto解越靠近y轴,表明中心畸变程度越小,干扰中心的干扰效果越差。从图中可以看出,越靠近y轴的解距离x轴越远。这表明,如果要得到更大的有效畸变区,使干扰范围更大,需要牺牲中心畸变程度作为代价;反之,若要获得更大的中心畸变程度,使中心点的干扰效果更好,有效的干扰范围就会变小。对比图4(a)和图4(b),通过增加一个阵元,当有效畸变区均达到最大时,三阵元情况下的中心畸变程度相比两阵元情况要更优,且三阵元情况下能达到的中心畸变程度在有效畸变区最小时也远远大于两阵元情况,这是因为增加阵元可以有效补偿相位和幅度,优化干扰系统参数。

通过对比图4中的5种不同阵元情况下的Pareto解分布,能够发现,5种情况下的有效畸变区间分布范围基本一致。也就是说,通过增加阵元或者环路的方法以获得更大的干扰范围效果并不明显。观察图4(c),四阵元情况下波前相位畸变效果最优,能够达到的有效畸变区间最大,同时能达到的中心畸变程度也最大。这表明,干扰效果并不随着阵元的数量越多而越来越好,在四阵元情况下,刚好形成两个干扰环路,环路之间相互补偿,因而达到最好的干扰效果。

根据图4(a)～图4(c)最右侧Pareto解的系统参数,得到了如图5～图7所示的合成波波前相位分布情况以及合成波功率分布情况。从图5(a)、图6(a)、图7(a)中可以发现,合成波相位在距离维上是呈周期变化的,这主要是因为波的周期性传播特性,但是在方位维上,相位发生畸变,这便是导致雷达测角产生误差最根本的原因。并且,畸变越严重,角度误差越大。对比分析3种情况下的波形畸变程度,可以发现,四阵元情况下干扰中心处畸变最严重,表明四阵元情况下干扰中心干扰性能最佳。

通过干扰方程可知,干扰范围主要受雷达能接收信号功率的阈值影响。通过对比图5(b)、图6(b)、图7(b)中的功率分布,可以发现,3种情况下的功率分布几乎一致,这也就是说,在上述3种情况下,干扰范围几乎一致。

4 结 论

本文对多元矢量合成的波形特征进行了分析,首先建立了一个典型的多元天线阵列模型,并对其合成波形相位、幅度进行公式推导计算,得出了多元矢量合成波形相位幅度的一般表达式。然后,用波前相位畸变区间和中心畸变程度作为目标函数,基于NSGA-II智能优化算法建立优化模型,并求得该模型下的Pareto解集,分析不同阵元合成情况下的Pareto解,认为在四阵元情况下的合成波中心畸变程度和畸变区间是最优的。通过增加阵元的方式能够有效地改善合成波形的中心畸变程度,但对于畸变区间的拓宽,并没有明显的改善。最后,基于Pareto解集中畸变区间最优的情况,仿真了阵元数分别为2、3、4情况下的合成波波前相位分布和功率分布,可视化地展示了多元矢量合成的波形特性。

虽然中心畸变程度与实际系统产生的误差角度之间没有直接的函数关系,但是普遍认为中心畸变程度越大,中心产生的误差角度也越大。有效畸变区越大,干扰扇面的范围也越大。相较于从单脉冲雷达测角体制方面来分析多元矢量合成的干扰方法,从自身出发,通过分析合成波束的有效畸变区来基本明确干扰范围,通过畸变程度大致判断中心位置的干扰效果,可以更好地设计干扰系统,而本文由于条件限制,并未考虑一些环境因素对系统性能的影响。接下来,将会更多地关注外部环境对干扰指标性能的影响并减小该影响,使多元矢量的合成方法更快地工程化。