附着式局域共振声子晶体薄板的带隙解析解

杨 文， 陈凯伦， 郭 旭， 陈泽宇， 刘长利

(华东理工大学 机械与动力工程学院，上海 200237)

自声子晶体(phononic crystal,PC)的概念提出以来，其在减振方面的带隙特性(在某个频率范围内抑制振动传播的特性)一直是研究热点。最先受到关注的是Bragg型声子晶体，其能在高频范围内实现对某一频段内振动的抑制，但要求晶格常数与振动波长在同一数量级内，这大大限制了其实际应用范围。随后Liu等[1]提出了局域共振型声子晶体(locally resonance phononic crystal,LRPC)，在同样的晶格常数下，其带隙频率要比Bragg带隙频率低两个甚至多个数量级[2]，这大大拓宽了声子晶体的应用范围，成为近年来研究的重点。

对于声子晶体带隙范围的计算，有传递矩阵法、集中质量法、平面波展开法，多重散射理论法，时域有限差分法和有限元法等多种方法[3-12]。在这些方法的基础上，发展了各种改进的方法。例如，改进的快速平面波展开法(improved fast plane wave expansion method,IFPWEM)[13]，通过消除跳跃不连续点和减少波矢量的数目，提高了算法的连续性与计算效率；α有限元方法(finite element method,FEM)[14]，通过α值改变软硬度，获得了一些可用于声子晶体设计的新特性。同样的，针对不同类型的声子晶体，也发展出了特定的计算方法，例如，扩展的平面波展开法[15]，其将平面波展开法(plane wave expansion,PWE)引入到均布动力吸振器的附着式声子晶体薄板的带隙计算中；质量重分布有限元方法(mass-redistributed finite element method,MR-FEM)[16]，用于计算具有硬包裹层的液体声子晶体；修正光滑有限元法(modified smoothed finite element method,M-SFEM)[17-18]，用于二维声子晶体中的流固耦合问题； Qian等[19]应用表面弹性理论和Timoshenko梁理论，将平面波展开法推广到压电声子晶体纳米梁的能带结构计算中。

以上基于平面波展开法或者有限元法等传统方法的改进方法，能更快或更准确地获得能带结构(色散关系)，但是这些方法仍属于数值方法，结果依赖于结构参数的选取，无法获得普适的能带结构规律，结果更无法应用于带隙的设计。

针对上述问题，本文利用四边简支局域共振声子晶体薄板的动力学方程，在X,Y方向模态截断阶数小于等于吸振器个数的条件下得到了振动位移的解析解。在此基础上，得到了阻抗表达式，并根据阻抗的概念阐述了带隙的形成机理，讨论了系统阻尼对带隙的影响，得到了无阻尼条件下带隙的解析解。最后，提出了带隙的设计方法。

1 模型与公式推导

1.1 四边简支声子晶体薄板

图1所示为四边简支声子晶体薄板，动力吸振器周期性地附加在均质薄板上，形成单面附着式局域共振型声子晶体薄板。薄板为四边简支，板长，宽，厚，密度，弹性模量，泊松比和模态阻尼比分别为a,b,h,ρ,E,v,ξp，其中各阶模态阻尼比相同[20]；吸振器间隔(晶格常数)为Δ，各吸振器弹簧刚度、质量、阻尼比，固有频率相同，分别为kd,md,ξd,ωd。在板上选取一点(x0,y0)作为激励点，其上施加一简谐激振力f0eiωt。

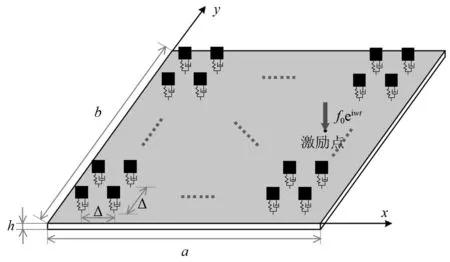
图1 均布动力吸振器的局域共振声子晶体薄板示意图Fig.1 Schematic diagram of a LRPC thin plate with a 2Dperiodic array of attached dynamic vibration absorbers(DVAs)

系统的动力学方程为

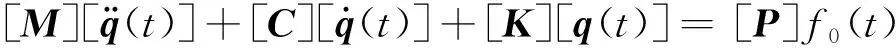
其中，位移向量可以表示为

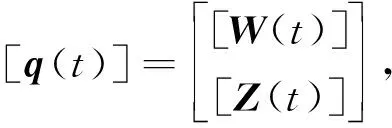
[W(t)]=[W1，1(t),W1，2(t),W1，3(t),…,WM,N(t)]T，

[Z(t)]=[Z1(t),Z2(t),Z3(t),…,ZQ(t)]T

(2)

式中：[W(t)]和[Z(t)]分别为薄板和动力吸振器的垂直位移向量；下标M,N分别为振动系统中X,Y方向上的模态阶数；下标Q为薄板上布置的动力吸振器个数。

[P]为外激励在薄板上的位置向量

[φ(x,y)]=[φ1，1(x,y),…,φm,n(x,y),…,φM,N(x,y)]T(3)

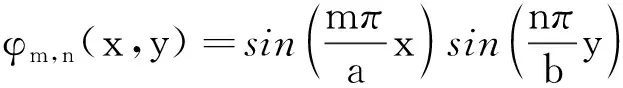
[M]，[C],[K]分别为质量、阻尼、刚度矩阵

(4)

在各吸振器参数相同的情况下，式(4)中各矩阵分别为

[Kpr]=[Krp]T=kd[[φ(x1,y1)],…,[φ(xQ,yQ)]],

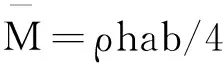
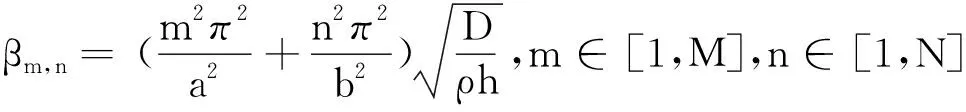
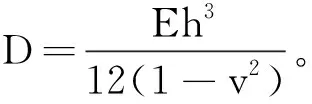
在简谐激励条件下，式(1)可以写为

(7)

将式(4)代入式(7)，消去[Z]，可得

[B][W]=f0[Pf]，
[B]=[K11]-[K12][K22]-1[K21]

，

[K11]=-ω2[Mp]+iω([Cp]+[Cr])+[Kp]+[Kr],

[K12]=[K21]T=iω[Cpr]+[Kpr],
[K22]=-ω2[Mr]+iω[Crr]+[Krr]

(8)

当X,Y方向的最大截断模态阶数小于等于X,Y方向周期性布置的动力吸振器的个数时(即M≤QX且N≤QY)，式(8)中矩阵[B]为对角阵。此时，[W]中各元素解耦，可以使用模态叠加理论计算振动位移，证明过程及约束条件详见参考文献[21]。

将式(5)各式代入式(8)，解得第m,n阶模态影响因子为

Y1=(1-g2)(f2-g2)-4fg2ξdξp-uf2g2，

Y2=2ξpg(f2-g2)+2ξdfg[1-g2(1+u)]

(9)

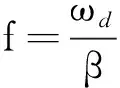
式中，wm,n为第m,n阶模态影响因子与模态振型的乘积。

1.2 阻抗表达式

根据式(10)，第m,n阶模态的位移公式可写为

式中，左边为简谐激振力与简谐运动响应的比值，即机械阻抗，其中φm,n为与位置及边界条件相关的函数。因此薄板中激励点(x0,y0)与点(x,y)之间第m,n阶的阻抗H为

(12)

将阻抗分为实部HR和虚部HI，代入式(9)中的Y1和Y2并化简，可得阻抗实部和虚部公式，它们都是激励频率ω与模态阶数m,n的函数

在第二章和第三章中，将分别在无阻尼和有阻尼情况下，讨论带隙的形成机理，并使用阻抗概念解释阻尼对带隙的影响。

2 无阻尼局域共振薄板与带隙解析解

无阻尼下，阻抗虚部为零，阻抗表达式(12)退化为

(15)

式中，阻抗实部为正时抑制振动，为负时没有实际的物理意义。

由模态叠加可知：在某一激励ω下，振动是被放大还是被抑制，取决于各阶模态叠加的结果。由于多阶模态的分析使得分析难度增大，可以认为薄板振动时一阶模态起主导作用[20]，这样仅需考虑薄板的一阶模态即可。

另一方面，由图2可知，阻抗实部随模态阶数的增大而增大，这是因为阻抗实部随薄板固有频率βm,n的增大而增大(见式(13))，同时薄板固有频率βm,n随模态阶数m,n的增大而增大(见式(6))。所以，第一阶模态的阻抗实部为正时，高阶阻抗也为正。

综上，求解式HR(ω,1,1)>0即可得到减振效果最好的频率范围，也就是带隙。

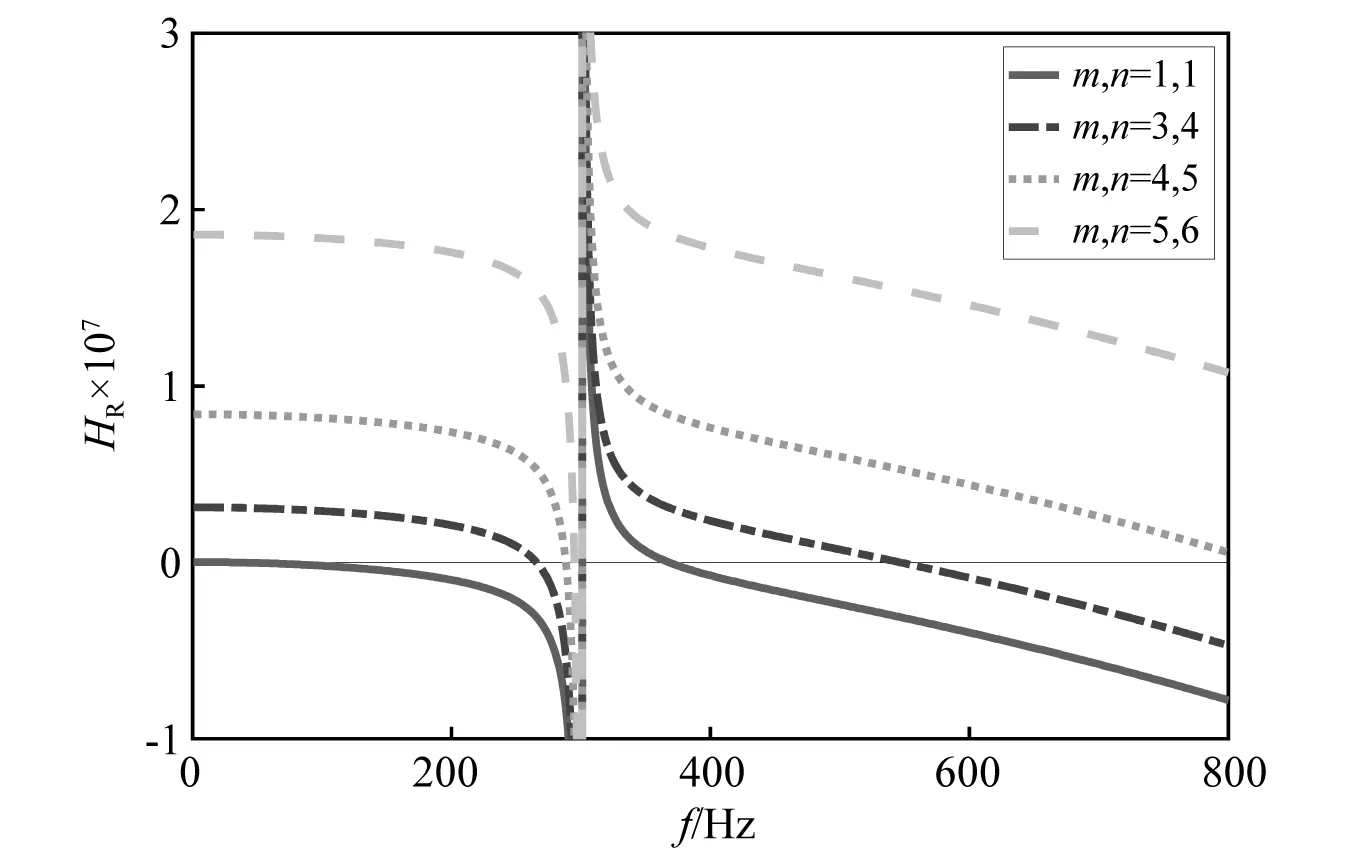
图2 无阻尼时不同模态阶数下的阻抗实部曲线Fig.2 Curves of impedance real part under different modal orders without damping

求解HR(ω,1,1)>0的解区间[fs,fe]，容易解得

(16)

式中，fs和fe分别为解区间的左值和右值，即带隙的起始频率和截止频率。

下面将通过扩展的平面波展开法和有限元法，计算其能带结构，并与带隙解析解式(16)的结果进行比较，验证解析解的正确性。

对于扩展的平面波展开法和有限元法，分别使用MATLAB和COMSOL作为计算工具。参数如表1所示。

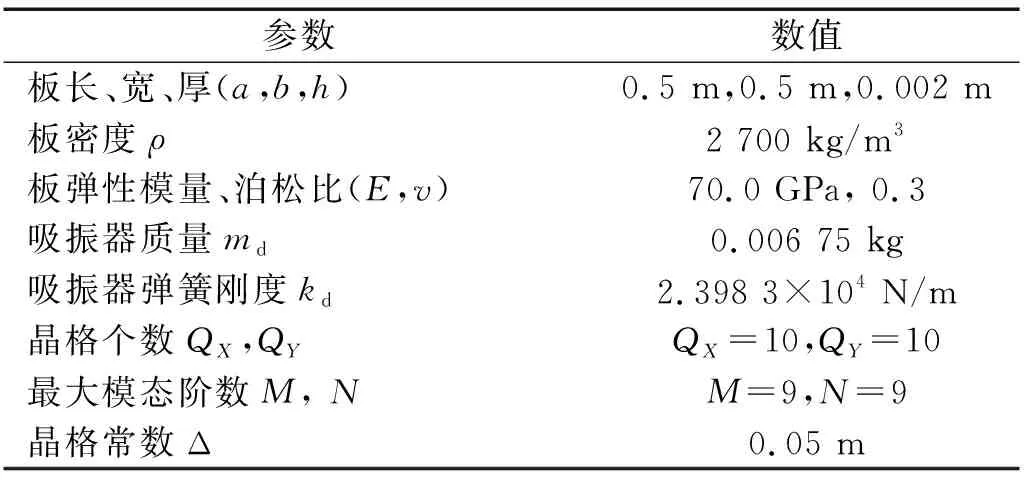
表1 材料参数Tab.1 Parameters of materials

扩展的平面波展开法和有限元法计算得到的能带结构如图3(a)所示，两者结果一致。使用有限元法计算得到位移传输特性曲线如图3(b)所示。计算能带结构和位移传输特性的有限元模型分别如图4(a)和图4(b)所示，在晶格有限元模型中，使用Floquet周期性边界条件。在薄板有限元模型中，薄板四边简支，吸振器通过节点连接在薄板上。不同方法获得的带隙范围如表2所示。由表2可知，相对于有限元方法和扩展的平面波展开法，解析解结果仅有2 Hz的误差，这说明带隙解析解是正确的。需要说明的是，研究中将吸振器简化为质量-弹簧-阻尼系统并通过节点而非接触面与薄板连接，因此解析和模拟结果与实际情况存在一定的误差，但当吸振器尺寸与薄板尺寸相差较大时，误差可以控制在一定范围内。

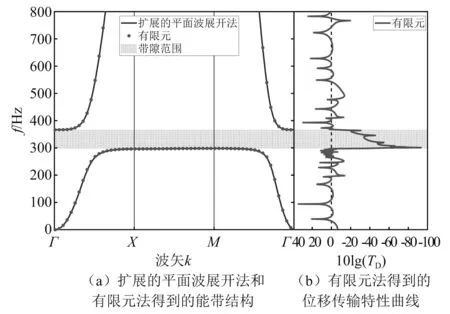
图3 能带结构与传输特性曲线Fig.3 Band structure and transfer characteristic curve

图4 有限元模型Fig.4 Finite element model

表2 不同计算方法得到的带隙范围

3 有阻尼局域共振薄板

本章将进一步根据阻抗公式及位移传输特性，讨论吸振器阻尼或板阻尼对带隙的影响。

3.1 吸振器阻尼的影响

当仅考虑吸振器的阻尼时，板阻尼比ξp=0，阻抗实部和虚部变为

(17)

(18)

比较图5和图6可知(所用材料参数同表1)，图5(b)中虚部峰值频率范围与图6中带隙范围基本一致。同时，随着阻尼峰值逐渐平缓，位移传输特性曲线中的波谷也随之变得平缓，体现了阻尼在减振中的作用。因此，当存在吸振器阻尼时，薄板带隙将以阻抗虚部为主导。带隙范围可根据虚部峰值所在频率范围估计。

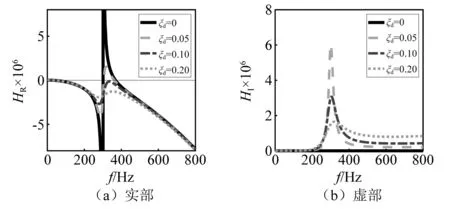
图5 当m,n=1,1时，不同吸振器阻尼比下的阻抗实部和虚部曲线Fig.5 Curves of impedance real and image part under different DVA damping ratios when m,n=1,1

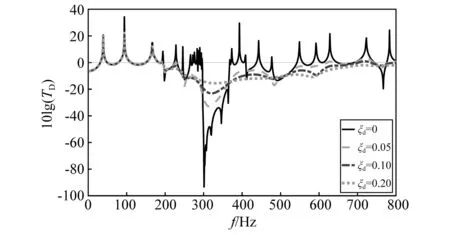
图6 不同吸振器阻尼比下的位移传输特性(有限元计算)Fig.6 Displacement transfer characteristic curves under different DVA damping ratios calculated through FEM

图6中，相对于无阻尼带隙，含吸振器阻尼时不存在明确的带隙边界，因此也不存在带隙解析解。这意味着，在含有吸振器阻尼时不能通过解析解计算带隙范围。

3.2 板阻尼的影响

当仅考虑板的阻尼时，吸振器阻尼比ξd=0，实部和虚部公式变为

(19)

(20)

由式(19)可知，阻抗实部不含板阻尼比；由式(20)可知，阻抗虚部与板阻尼成正比，如图7所示。由图7不同板阻尼比下的阻抗实部和虚部曲线可知，在板阻尼下，阻抗虚部较阻抗实部低两个数量级，这意味着阻抗虚部对带隙的影响远小于实部，可以忽略虚部阻尼的作用，将板阻尼问题退化为无阻尼问题。因此，在仅含板阻尼的情况下，带隙基本不变且无阻尼带隙解析解式(16)同样适用，如图8所示。

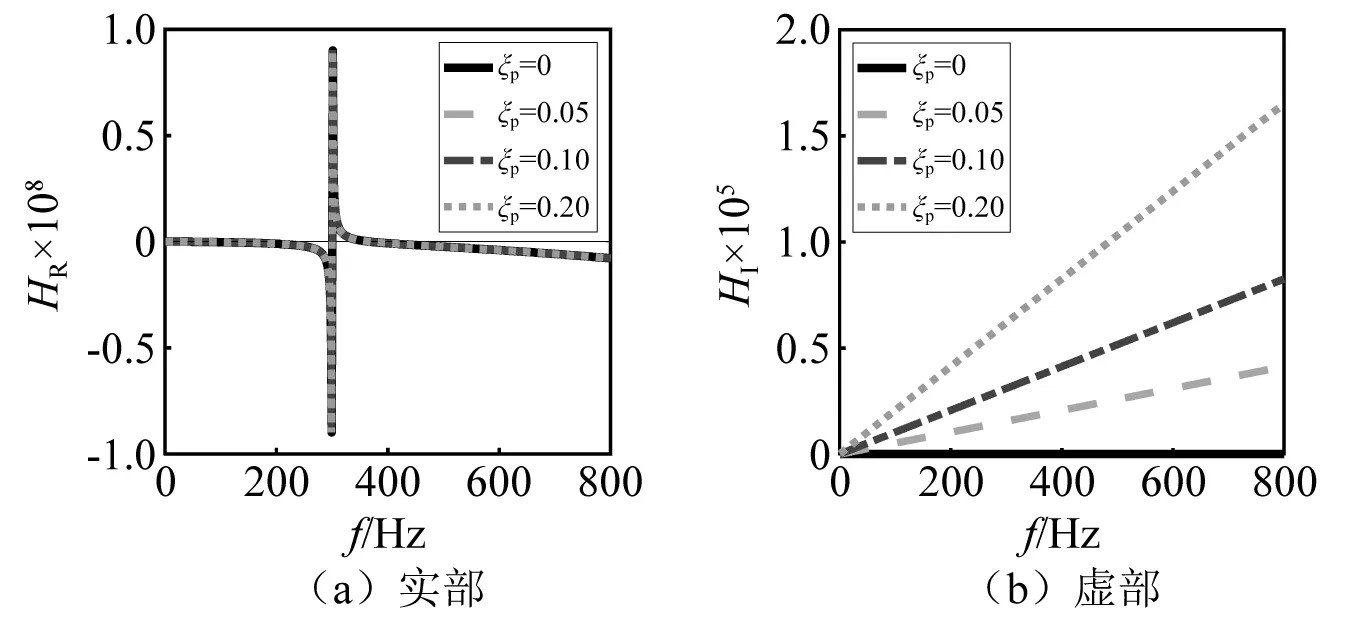
图7 当m,n=1,1时，不同板阻尼比下的阻抗实部和虚部曲线Fig.7 Curves of impedance real and image part under different plate damping ratios when m,n=1,1

综上所述，板阻尼对带隙的影响很小，而吸振器阻尼对带隙有显著影响。因此，在研究含阻尼声子晶体薄板的带隙时，可以忽略板阻尼的影响，仅讨论吸振器阻尼的影响。在不含吸振器阻尼的情况下，可以使用带隙解析解式(16)计算带隙范围。

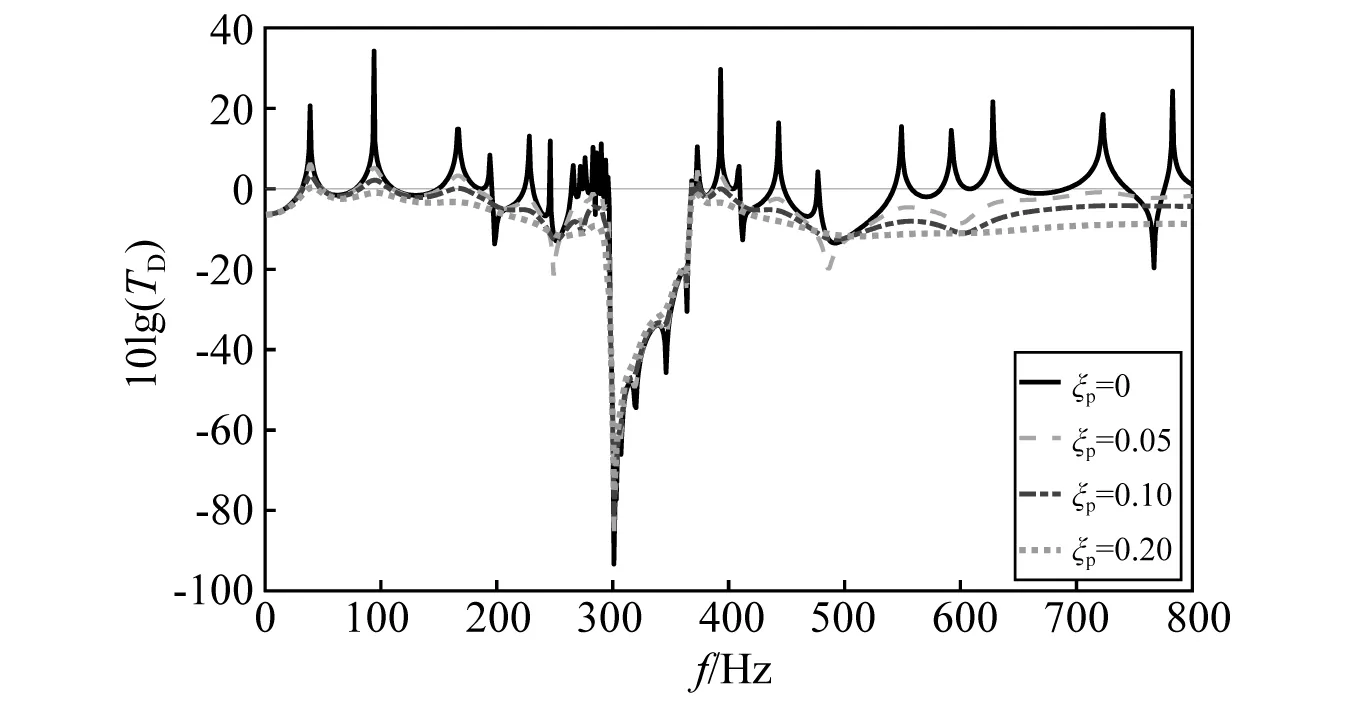
图8 不同板阻尼比下的位移传输特性(有限元计算)Fig.8 Displacement transfer characteristic curves under different plate damping ratios calculated through FEM

4 带隙的设计

局域共振声子晶体薄板在不含吸振器阻尼的情况下，可以使用带隙解析解计算带隙范围。反之，也可以使用带隙解析设计带隙。

式(16)及其中各个变量的表达式为

(21)

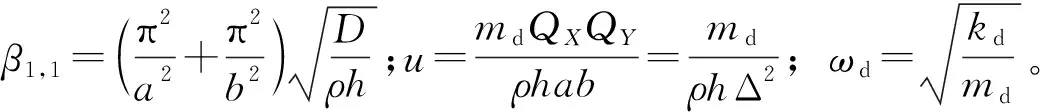
由式(21)中的变量可知，带隙的范围由以下三个方面决定：①板特性——板尺寸(a,b,h)，板材料的物理特性(D,ρ);②吸振器个数——QX,QY(或晶格常数Δ);③吸振器特性——吸振器质量md，弹簧刚度kd。

若要设计四边简支薄板的带隙，首先确定板的特性a,b,h,D,ρ,β1,1;然后通过改变吸振器个数QX,QY(或者晶格常数Δ)、吸振器质量md和弹簧刚度kd即可设计带隙的起始频率、截止频率和带隙范围。

5 结 论

本文根据四边简支的局域共振声子晶体薄板动力学方程，在一定条件下得到了系统振动位移的解析解，在此基础上讨论了带隙与阻抗的关系。研究结果表明，在无阻尼情况下，可以明确地给出带隙起始频率和截止频率的解析解，与有限元及扩展的平面波展开法所得结果一致。在有吸振器阻尼时，带隙没有明确的边界，无法使用解析解计算带隙范围；而板阻尼对带隙没有影响，仍可按照解析解计算带隙。

利用本文提出的带隙解析解公式，可以直接计算带隙范围，而无需计算能带结构，从而提高了获得带隙范围的效率。同时可以方便地设计四边简支声子晶体薄板的带隙，摆脱了数值方法通过参数试凑或优化来设计带隙的局限性。