准静态压缩载荷作用下U型折叠式夹层板芯层变形机理研究

李 遥， 刘 昆， 沈超明， 王加夏

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

随着船舶与海洋工程装备的发展，船舶对结构安全性、功能性和轻量化的要求日益迫切。相比于传统的船舶加筋板架结构，折叠式夹层板结构具有比强度高、焊接变形小、抗冲击性能好、设计性强等优点[1-2]，受到船舶行业的青睐，各国海军、船级社、科研院所陆续开展了夹层板各方面的研究工作[3]。夹层板优越的力学性能得益于特殊的芯层结构，因此，研究载荷作用下夹层板芯层的变形模式及受力特征对于提升船舶的设计水平具有重要意义。

对于塑性变形行为，Jones[4]从理论、数值及试验3个方面进行了系统的研究，归纳了研究结构受力特征和变形模式的基本理论和方法。张延昌等[5-7]通过试验及仿真对夹层板的V型芯层结构在屈曲过程中的受力特点，并讨论了变形模式对结构吸能的影响。Xue等[8]比较了蜂窝芯、折叠结构芯和锥体桁架芯在同一工况下的吸能特性，通过分析芯层的受力特点优化了结构参数。在此基础上，Ferri等[9]和Lee等[10]进一步通过试验和仿真研究了蜂窝芯、折叠结构芯和锥体桁架芯的动力响应和变形特征，系统地分析夹层芯材的抗压性能和抗冲击性能。上述工作从试验和仿真两方面对夹层板芯层的受力和变形开展研究，得到了准确的变形特征，但在设计及评估夹层板性能时往往耗时较长。对此一些学者从理论解析入手进行研究，Xue等[11-13]规避了复杂的芯层变形带来的繁琐计算过程，将蜂窝夹层板和折叠式夹层板等效为正交异性板，计算出了面内载荷下的夹层板的应力和位移。Coté等[14]在研究金属蜂窝夹层板芯层的屈曲问题时，并未完全忽略芯层变形而是简化了芯层力学特征和变形特性，通过数值仿真拟合以及理论推导得到了较为准确的解析公式。此外，高振国等[15]在研究强肋框及交叉结构变形机理的理论方法，对研究夹层板芯层结构的力学特征和变形模式具有借鉴意义。进行理论解析时，学者大多将折叠式夹层板进行等效处理，忽略夹层板芯层的实际变形特点和力学特征，而这会对计算结果产生一定的影响。因此，在建立力学模型进行理论解析时需要充分考虑夹层板芯层的变形模式。

本文通过设计开展U型夹层板模型的准静态压缩试验以及相关数值仿真计算，分析U型夹层板在准静态压缩载荷作用下结构变形过程的特点；在此基础上，确定夹层板的变形模式，运用塑性力学理论，推导得到瞬时结构变形抗力的解析计算公式，并与试验结果进行验证。本文的研究结果对夹层板压皱性能设计及评估具有指导意义。

1 试验及仿真研究

1.1 试验介绍

试件为激光焊接U型折叠式夹层板，主要包括上下两块面板及U型芯层，如图1所示。面板的厚度均为1.5 mm，芯层壁板的厚度为1 mm。芯层结构的高度为100 mm。试件包括4个芯层单元，芯层单元的尺寸(见图1(b))，同时在左右两侧各增加40 mm方便试验时对试件进行约束。试件总体尺寸为580 mm×200 mm×100 mm。材料为Q235低碳钢，该批次的1 mm和1.5 mm Q235板材的力学性能，如表1所示。工装主要包括支撑架、承载板和压头，试件的上、下面板分别与承载板、支撑架通过约束块和螺栓连接在一起，防止夹层板发生侧向位移，损坏试验设备，如图2所示。支撑架两侧挡板尺寸为200 mm×250 mm×20 mm，支撑架底板尺寸为1 000 mm×350 mm×20 mm，承载板尺寸为700 mm×250 mm×30 mm。圆柱体压头的半径为110 mm，材料为硬度较高的高碳铬轴承钢，在受载情况下压头变形忽略不计。共进行3次试验，试件编号分别为U1，U2，U3。

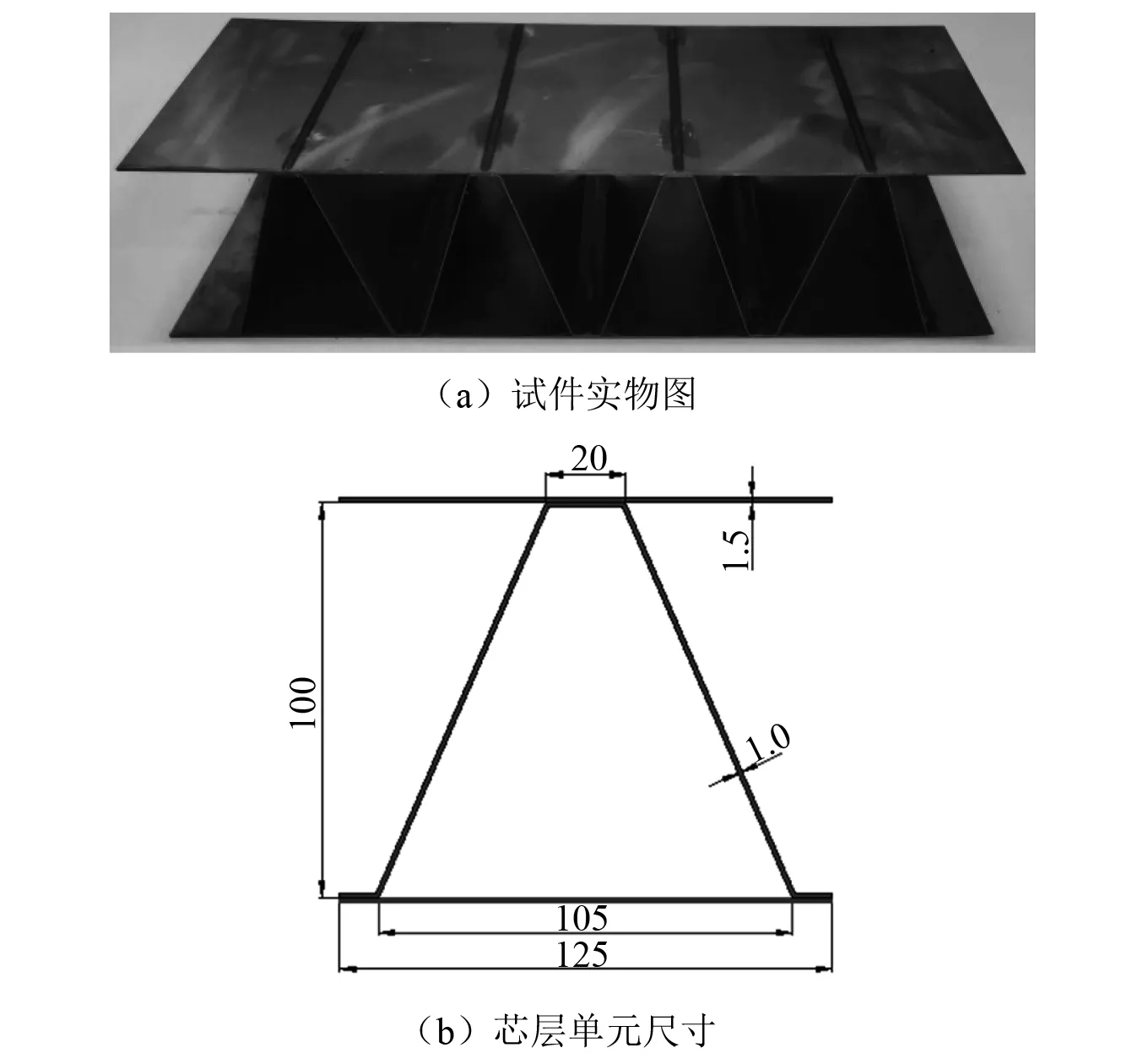
图1 U型夹层板试件及尺寸(mm)Fig.1 Specimen and geometry of specimen(mm)

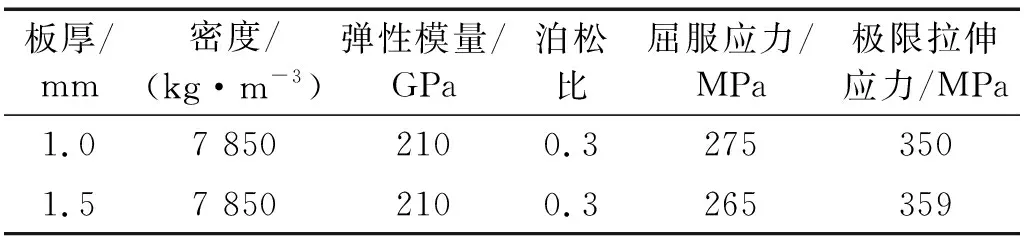
表1 试件力学性能参数

图2 试验装置及原理Fig.2 Experimental setup and schematic

准静态准静态压缩试验的试验设备及原理图(见图2)。试验采用电液伺服万能试验机，该设备最大施加载荷为100 kN。试验时，试验机压头作用在承载板中心处，加载预压力500 N，使夹层平面平整，确认加载均匀性，以10 mm/min的恒定速度加载。压头位移以及结构抗力由万能试验机记录，采样频率为20 Hz。

1.2 有限元仿真

基于上述结构尺寸，利用非线性有限元软件ABAQUS建立有限元模型，坐标轴x，y，z方向分别为夹层板的长度、高度和宽度方向。夹层板结构采用4节点减缩积分壳单元(S4R)，网格特征尺寸取5 mm；承载板和支撑架采用8节点六面体线性减缩积分体单元(C3D8R)，网格特征尺寸取5 mm；压头为刚体。夹层板结构材料为低碳钢Q235，密度为7 850 kg/m3，泊松比为0.3，弹性模量为210 GPa，为简化计算夹层板统一采用1 mm的Q235钢板的材料属性。采用“组合材料关系曲线”描述材料的应力应变关系[16]，如图3所示。

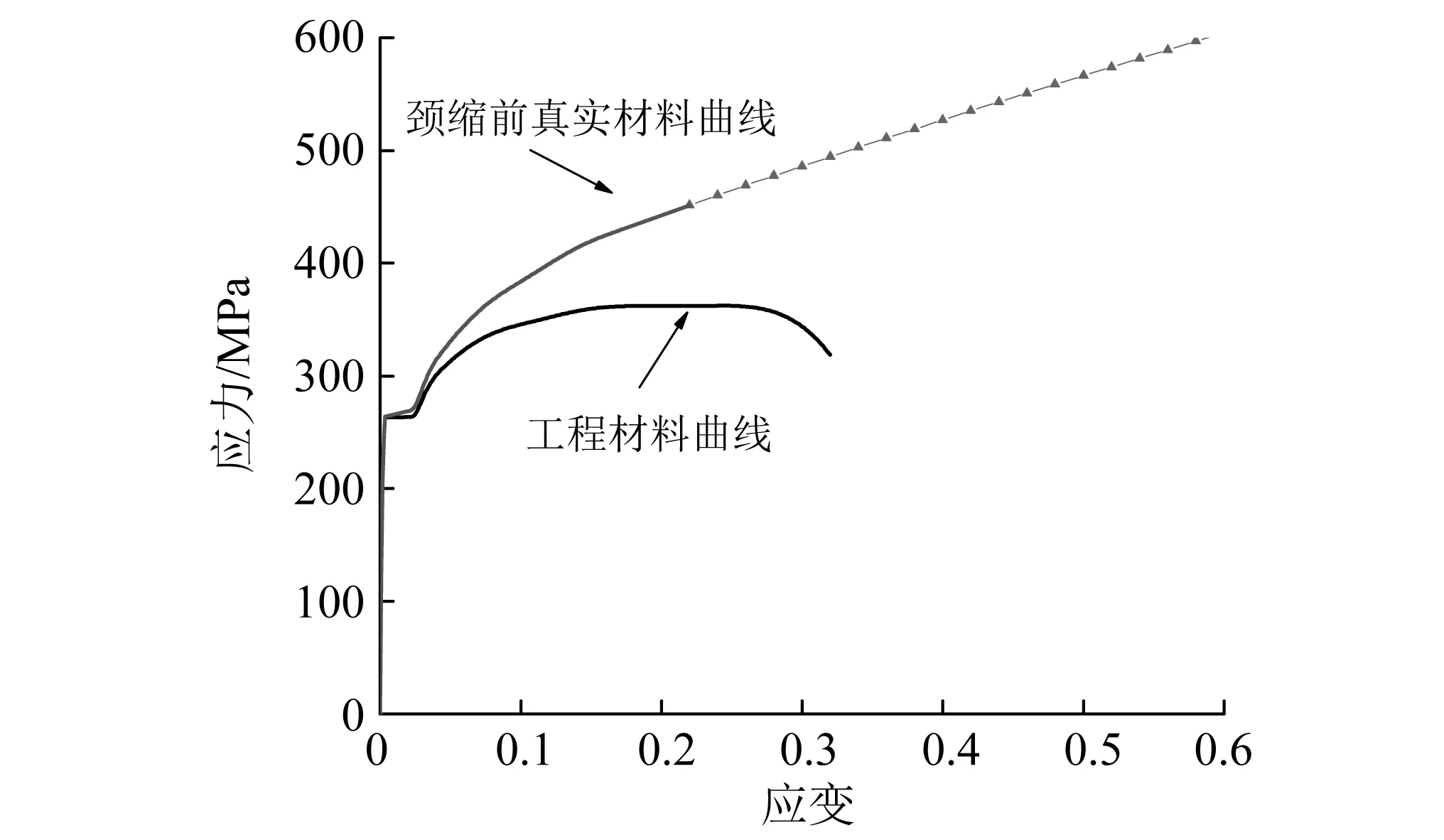
图3 组合材料关系曲线Fig.3 Combined material relationship

材料达到颈缩之前，基于工程应力-应变关系曲线，利用式(1)和式(2)计算得到的真实应力-应变关系曲线

σu=su(1+eu)

(1)

εu=ln(1+eu)

(2)

式中：su，eu分别为工程应力和应变；σu，su分别为真实应力和应变。

发生颈缩以后，采用基于幂指数函数和线性函数得到的加权平均法得到[17]

(3)

式中，w指未知的权值常数。多次仿真计算后发现当w=1时，仿真结果与试验结果吻合较好。

在试验过程未观察到夹层板出现撕裂破坏现象，因此不定义材料的失效准则。结构之间定义通用接触，摩擦因数取0.3[18]，上下面板两端分别与承载板、支撑架定义绑定约束。仿真中压头以0.02 m/s的恒定速率进行加载。约束压头垂向外的其他自由度，即：Ux=Uz=URx=URy=URz=0；支撑架底面刚性固定，即：Ux=Uy=Uz=URx=URy=URz=0。

初始变形对芯层壁板的失稳变形有显著影响，且1 mm薄板易于产生焊接变形。针对这个问题，以往的研究[19]将塑性变形作为初变形陷引入网格模型的芯层壁板中部。Radford等[20]发现夹层板的响应对所引入的初始变形值的精确程度并不敏感。本文通过在芯层壁板上下两端拉直细线的方法仔细测量芯层壁板中的初始变形，即拉直细线的细线为理想位置，测量芯层壁板实际偏离的方向和距离。在芯层中间处引入垂直芯层壁板1 mm的初始变形，方向如图4所示。夹层板有限元仿真模型如图5所示。

图4 试件的初始变形Fig.4 Initial deformation introduced in the specimen

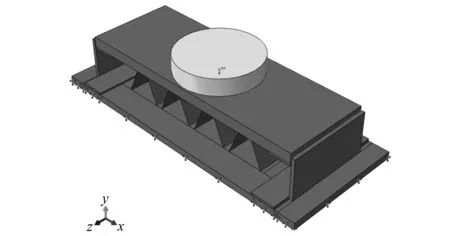
图5 有限元仿真分析模型Fig.5 Model of the corrugated cores sandwich panel

2 结果分析

2.1 变形过程及特点

图6～图8为试件U1，U2，U3受准静态压缩载荷时的变形情况。受制造工艺焊接变形和材料性能等因素的影响，试验中试件芯层的变形过程差异较大，但依据压皱过程中相邻芯层板是否互相接触，可将芯层单元的变形过程归纳为两类，如图9所示。结合图10的结构抗力-位移曲线，可把整个变形过程分为3个阶段。阶段Ⅰ：芯层受面内载荷之后，芯层壁板发生失稳并在中间处形成塑性铰线，同时芯层壁板与面板连接处也将形成塑性铰线。此时，若相邻的芯层板同时发生向内的屈曲，将产生第一类变形过程。随着压皱深度的增加，相邻芯层板在中间形成塑性铰线的圆弧区域相互接触，之后相邻芯层板相互挤压向下运动并同时与面板接触，变形进入阶段Ⅱ(见图9(a)D点)。若相邻的芯层板同时发生向外或者分别发生向内、向外的屈曲变形，将产生第二类变形过程，随着压皱深度的增加，相邻夹芯层板折叠后直接与面板接触(见图9(b)C点、D点)。变形在阶段Ⅱ过程中，随着压皱位移的增加，与面板相互接触的一半芯层均不再产生明显变形，对于第一类变形过程而言，另一半芯层板从中位置处同时向外屈曲并形成塑性铰线；对于第二类变形过程而言，另一半芯层板从中位置处分别向内和向外的屈曲并形成塑性铰线。最后整个芯层被压实。准静态压缩载荷作用下芯层的变形情况均由这两类变形过程组合得到：U1包含4个第二类变形过程；U2包含3个第二类变形过程，1个第一类变形过程；U3可看作包含2个第一类变形过程和2个第二类变形过程。

图6 试件U1受压变形过程(位移为15 mm，45 mm，60 mm)Fig.6 The deformation process of specimen U1 (displacement: 15 mm, 45 mm, 60 mm)

图7 试件U2受压变形过程(位移为15 mm，45 mm，60 mm)Fig.7 The deformation process of specimen U2 (displacement: 15 mm, 45 mm, 60 mm)

图8 试件U3受压变形过程(位移为15 mm，45 mm，60 mm)Fig.8 The deformation process of specimen U3 (displacement: 15 mm, 45 mm, 60 mm)

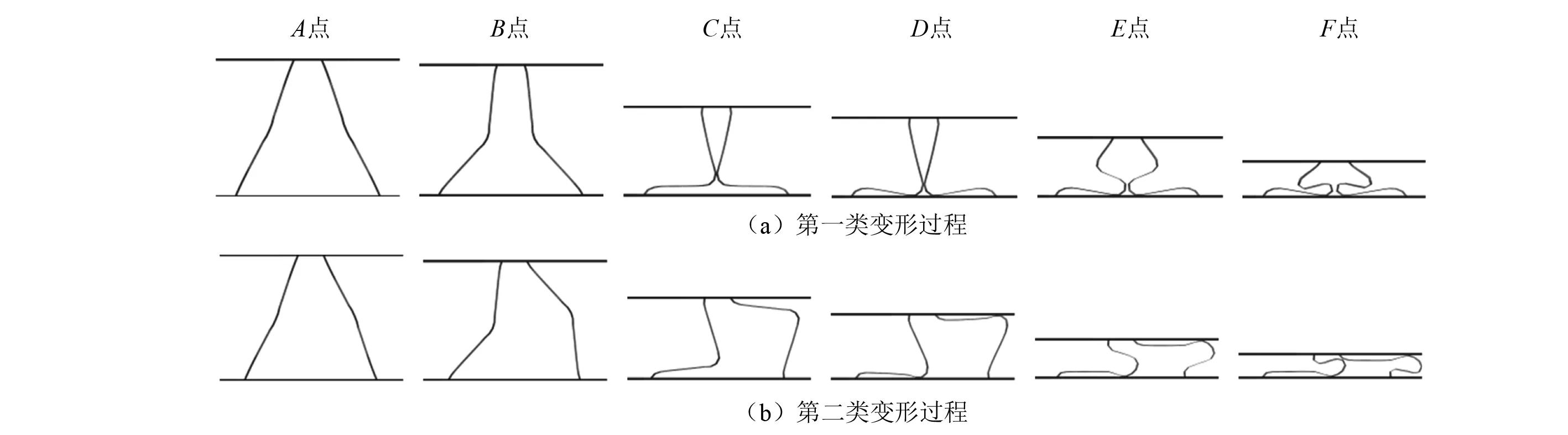
图9 夹层板受压变形过程分类Fig.9 Classification of specimen deformation process

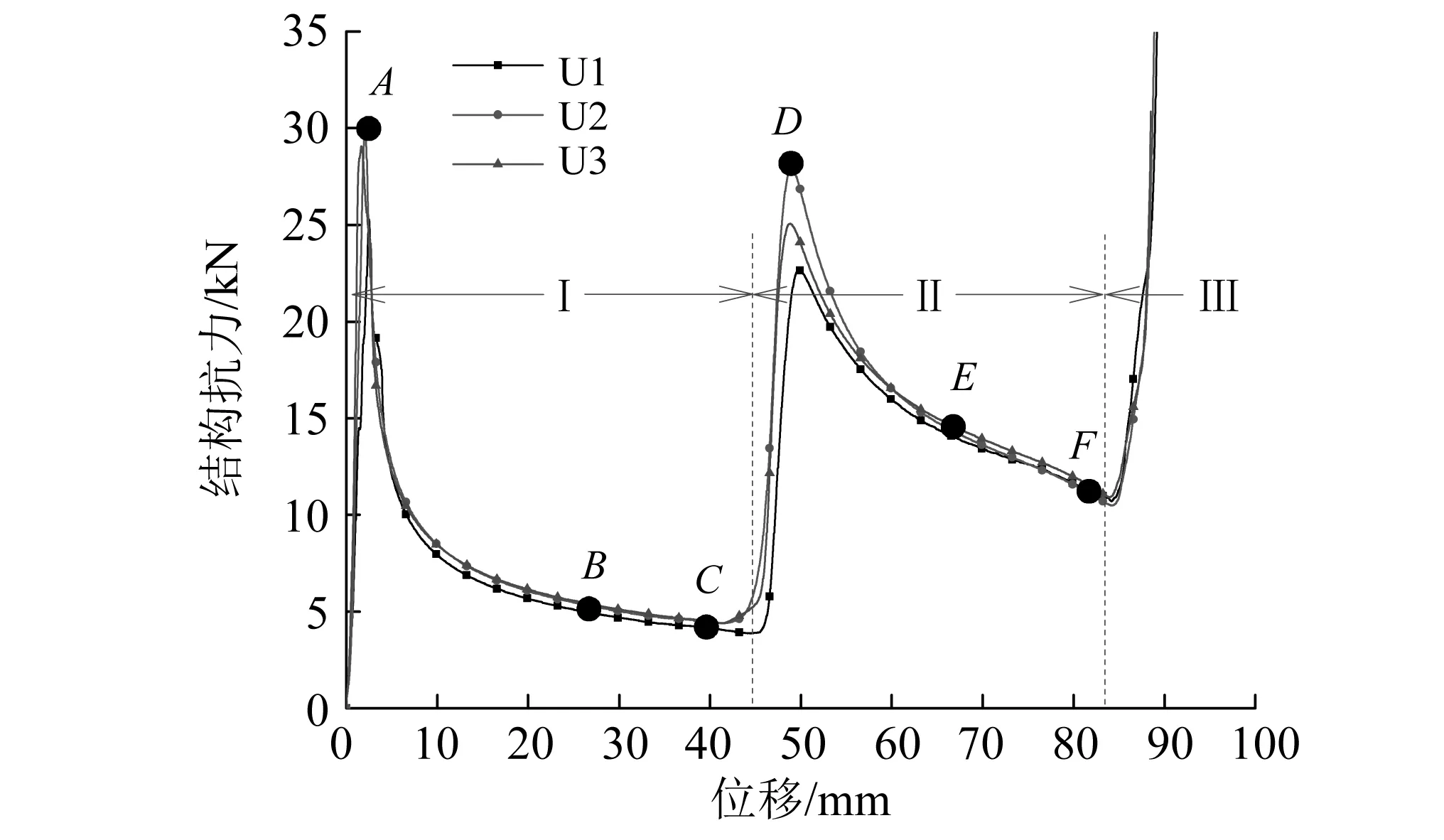
图10 各试件结构抗力-位移曲线Fig.10 Curves of resistance force versus compressive displacement

2.2 准静态压缩载荷

试件U1，U2，U3的试验所得的结构抗力-位移曲线(见图10)。尽管3个试件芯层的变形情况差异较大，但结构抗力-位移曲线重合度很高且误差主要体现在第一和第二峰值处，芯层出现较多的第一类变形模式时，夹层板最大结构抗力更大。各试件试验与仿真结果的对比，如图11所示。从图11可知，芯层受压后抗力立即达到第一峰值，之后芯层失稳抗力快速下降并趋于稳定。试件U2和U3在压缩至30～40 mm处时，结构抗力出现了微小的增加，主要是因为试件U2和U3的压缩过程中出现了第一类变形过程，C点和D点的变形过程(见图9(a))，在第一类变形过程中，芯层壁板首先接触，使结构抗力上升。30～40 mm处结构抗力增加仅出现在仿真中，试验中未出现，主要原因是试验过程中，芯层壁板相互接触时整个芯层壁板产生一定的屈曲并过渡到阶段Ⅱ，因此结构抗力没有增加。仿真中芯层壁板相互接触后芯层壁板整体向下压缩未出现整体屈曲，因此仿真结构抗力出现增加。随着压皱位移的增加，芯层和面板相互接触，抗力出现第二峰值，之后芯层再次发生失稳，载荷逐渐下降，当位移达到85%左右的芯层高度时芯层被压实。在第一峰值处，试验结果小于仿真结果并且试验峰值较晚出现，这由于压头刚接触时整个试验系统并未稳定，经过一定的压皱位移才能达到峰值。第二峰值处，试验结果同样滞后于仿真结果，主要是因为在仿真是较为理想的状态，芯层与面板相互接触即产生第2个峰值，而在试验过程中，芯层与上下面板接触并产生一定的屈曲之后才会产生第2个峰值。另外，在第2个峰值处仿真结果出现了明显的波动，这是由于芯层与面板接触部位发生了一定滚动，起到了卸载的作用(见图9(b))。除了峰值处，试验结果和仿真结果的误差普遍小于8%。

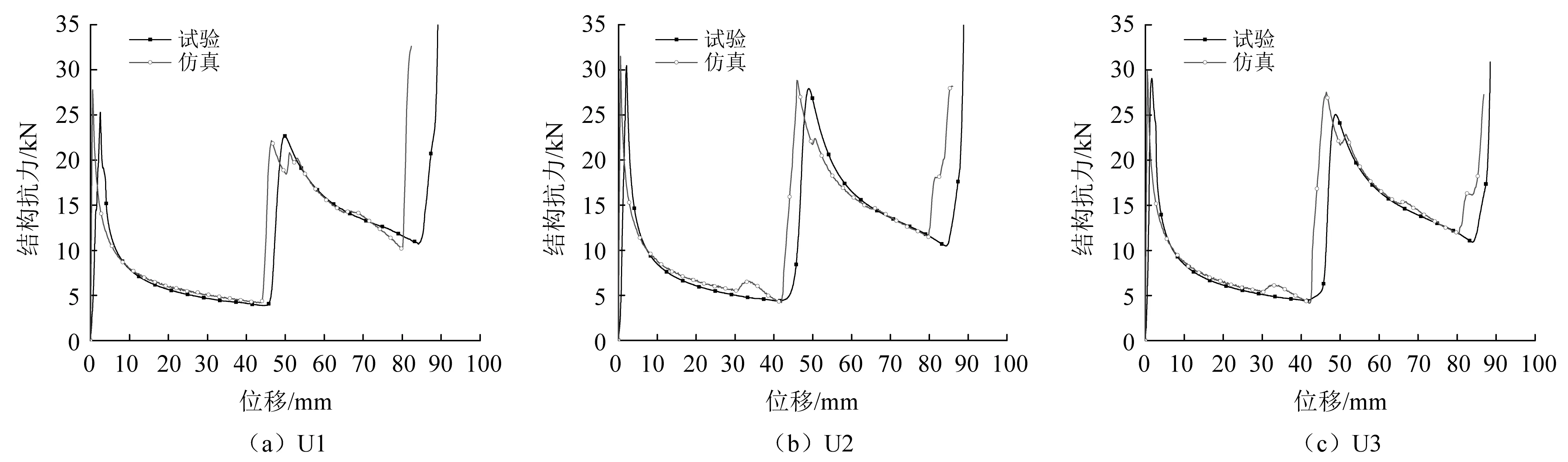
图11 试验与仿真结果对比Fig.11 Comparison between FEA and experiment

总体而言，试验和仿真结果吻合较好，仿真较准确地模拟了试验过程。因此，可以参考仿真结果研究在面内准静态压缩载荷作用下结构的解析计算方法。

3 压皱变形的解析

根据试验及仿真结果，对夹层板变形过程做出如下假设：

(1)整个压皱过程中，面板几乎不发生变形，因此面板的吸能忽略不计；

(2)夹层板芯层的变形分为弹性变形和塑性变形，弹性变形的吸能忽略不计；

(3)与上下面板连接处的一小段芯层未参与芯层的整体变形，阶段Ⅰ中忽略不计，但阶段Ⅱ过程中参与变形的芯层板变短，因此解析中予以考虑；

(4)阶段Ⅰ的压皱位移占总高度的45%，阶段Ⅰ和阶段Ⅱ的总压皱位移占总高度的85%左右。

通过以上分析和假设，得到夹层板受压皱力时的变形模式如图12所示，两种变形模式具有如下特点：

①在阶段Ⅰ过程中，自上而下第一、第二条塑性铰之间的板距离与第二、第三条之间的板距离比为1 ∶1，即AC∶CD=1 ∶1;

②在阶段Ⅱ过程中，AB，BC共线且各塑性铰之间的板高度比AB∶BC=1 ∶1。

图12 夹层板两种变形模式Fig.12 Two deformation modes of the U-type corrugated cores sandwich panels

基于夹层板变形模式，运用塑性力学理论，可以推导出结构抗力的功率等于内部能量耗散率，可表示为

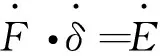
(4)

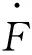
对于夹层板而言，内部能量耗散率塑性铰线的转动能，可表示为

(5)

(6)

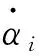
变形模式一阶段Ⅰ：

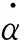
δ=lsinθ-lsinθ1cosα

(7)

式中：θ1=arctan[(h-δ)/(b-a)]，为了简化计算，在计算过程中取θ1≈θ，显然角度值会比实际偏大，故在实际计算时引入修正因子λ=0.8～1.0。

(8)

(9)

将式(9)代入式(5)，得到第一阶段过程中的弯曲能量耗散率

(10)

式中：n为出现该变形模式的芯层单元的个数；L为塑性铰的长度。

压皱过程中准静态压缩载荷为：

(11)

变形模式一阶段Ⅱ：

从试验和仿真中发现，在阶段Ⅰ过程中，芯层板中间屈曲处出现了较大的圆弧，且芯层相互接触时圆弧整体不产生变形。在阶段Ⅱ过程中，塑性绞线出现在圆弧的上方(见图11)，因此，阶段Ⅱ过程中参与变形的芯层板约为0.4l。同时考虑到假设(3)，阶段Ⅱ过程中参与变形的芯层板取为0.35l。

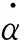
δ=0.35lsinγ-0.35lsinγ1cosβ

(12)

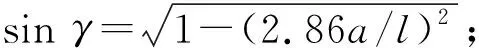
(13)

(14)

将式(14)代入式(5)，得到阶段Ⅰ过程中的弯曲能量耗散率

(15)

式中：n为芯层单元的个数；L为塑性铰线的长度。

压皱过程中压皱力为

(16)

准静态压缩载荷作用下U型夹层板的瞬时变形抗力解析计算公式为

(17)

对于变形模式二以同样的方法计算，得到相同的瞬时结构抗力表达式，其中sinγ=

4 解析方法的验证

通过将试验与仿真结果对本文提出的解析计算法并进行验证，模型主要参数如表2所示。

表2 模型主要参数

把试验结果、仿真结果和解析计算结果进行汇总，结果如图13所示。在第1个峰值处，与试验结果相比仿真结果和解析结果更接近，这是由于仿真和解析可认为是较为理想的状态。阶段Ⅰ过程中，仿真结果、解析结果和试验结果三者的变化趋势一致，吻合很好。在第2个峰值处，解析峰值和试验峰值出现的位置相同，证明解析方法中通过假设压皱位移能准确预测峰值出现的位置。在图13(a)和图13(c)中第二峰值处的解析结果大于仿真结果和试验结果，这主要是U1和U3试件的芯层出现较多的第二类变形模式，芯层与面板接触部位发生了一定移动，起到了卸载的作用。阶段Ⅱ过程中，与解析结果相比仿真结果和试验结果吻合的较好，原因在于解析方法仅考虑塑性绞线转动吸能，而真实情况下变形更复杂，随着压皱位移的增加，塑性绞线还产生了微小的滚动和滑移，同时阶段Ⅰ中与上下面板接触的部分芯层也会发生微小的变形。阶段Ⅱ过程中仿真结果、解析结果和试验结果三者的误差普遍在10%以内。总体来说，本文解析结果、仿真结果和试验结果吻合较好，验证了解析方法的可行性。

图13 瞬时结构抗力结果对比Fig.13 Comparison of resistance forces

5 结 论

本文主要研究了U型夹层板在面内准静态压缩载荷作用下的变形损伤机理。通过对准静态准静态压缩试验以及数值仿真中变形过程的研究，提出了U型夹层板变形的解析计算方法。主要结论有：

(1)由试验及仿真结果发现，压缩过程中共分为3个阶段。前2个阶段的压缩过程，是芯层壁板失稳并从中间处产生屈曲，之后面板与芯层壁板互相接触，可使用塑性铰理论对前2个阶段进行解析计算；对于阶段Ⅲ，芯层接近压实，变形模式较复杂，理论推导有待完善。

(2)受准静态压缩载荷时因制造工艺等因素的影响出现会两类变形模式，但两类变形模式的瞬时结构变形抗力曲线重合度较高，差异集中体现在2个峰值处，芯层出现较多的第一类变形模式时，夹层板最大结构抗力更大。

(3)通过与仿真和试验的结果的对比发现，本文提出的解析计算方法能较好的预测夹层板在面内准静态压缩载荷下的结构变形抗力，适用于夹层板压皱性能初期设计及性能的快速评估。