整体感知口诀 重历创造过程

张国梅 汤佳锋

【摘   要】5以内的乘法口诀是学生学习乘法口诀的开始。针对大部分学生会背乘法口诀却不知其意的学情，可尝试对5以内乘法口诀的教学进行整合。通过点阵模型引出乘法口诀，让学生在经历“数一数、列一列、算一算、编一编、理一理、用一用”等数学活动后，发现乘法口诀的编写规律，厘清乘法算式、乘法含义、乘法口诀、同数连加算式之间的联系。

【关键词】乘法口诀;数形结合;几个几

乘法口诀是我国古代筹算中进行乘法、除法、开方等运算的基本计算规则，已有两千多年的历史，体现了我国语言文字的独特魅力。在调查中发现，大约80%的学生能够熟练地背诵5以内的乘法口诀，但是对于乘法算式和口诀之间的联系并不太理解。因此，教师需要重新审视乘法口诀教学的起点与生长点，让不同层次的学生在教学中都有所收获。笔者尝试对“5以内的乘法口诀”的学习进行适当整合，通过“数一数、列一列、算一算、编一编、理一理、用一用”等活动，让学生进一步认识乘法的含义，全面地认识乘法口诀，沟通乘法算式、乘法意义、乘法口诀、同数连加算式之间的联系，构建起多元的乘法表征形式。

一、数形结合，发现乘法口诀编写规律

教材中“1～5的乘法口诀”的学习是借助具体的情境来组织的。整合后的教学，如果仍沿用教材中的情境图，则显得杂乱无章。因此教师尝试采用小方块这一几何图形，统一表征情境。

（一）结合图式，列出乘法题组

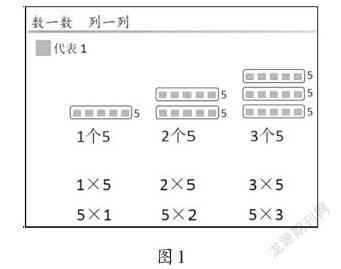
用一个小方块代表1，教师出示5个小方块，问：这是几？学生回答后，教师把这5个小方块圈起来，继续追问：这是多少？通过让学生“数一数”，引出“1个5”。之后让学生“列一列”，列出相应的乘法算式。用同样的方式，列出“2个5”“3个5”的乘法算式，逐步形成板书（如图1）。

在“数一数”中，通过将5个分散的小方块演变为圈在一起的5个小方块的过程，学生更好地理解了“有几个几相加”的乘法含义。而在“列一列”中，教师没有让学生计算结果，而是让学生通过“有几个几相加”感受5的乘法算式的变化规律。

（二）计算结果，初创乘法口诀

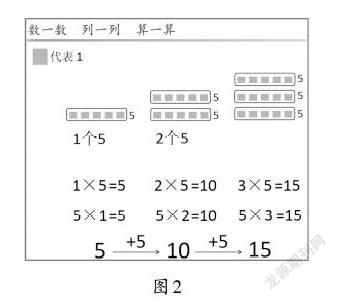
在列出上述3组乘法算式之后，教师依次让学生算出乘法题组的结果：只有1个5就是5;有2个5相加就是在5（1个5）的基础上再加1个5，是10;有3个5相加就是在10（2个5）的基础上再加1个5，是15。通过连加计算得到结果，使学生进一步理解乘法的含义（如图2）。

1.“三五十五”的口诀编写

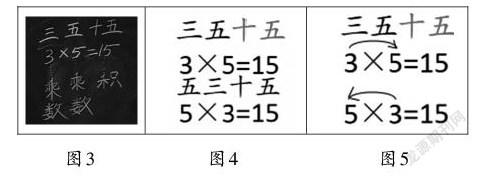
教师追问“3×5”有没有其他方法可以算出结果，引出乘法口诀“三五十五”，并问学生这句口诀代表的意思，以及它的组成部分。根据学生的回答，引出乘法各部分名称，让学生知道乘法口诀由两个乘数、积组成（如图3），并建立乘法算式与乘法口诀之间的联系。教师紧接着问：“‘5×3=15’的乘法口诀应该是什么？”有学生提出“五三十五”（如图4），教师进一步追问：要不要这句口诀呢？根据学生的回答，概括得出：两句口诀积相同，口诀中小的乘数在前更顺口，同时教师在算式中用标箭头的方式演示，发现只需留下“三五十五”这一句口诀即可（如图5）。

经历“三五十五”口诀的编写过程，学生沟通了乘法口诀与乘法算式之间的联系，掌握了乘法口诀的基本结构。在理解各部分数的含义时，教师自然地引出“乘数”与“积”，并概括了乘法口诀的基本结构，为后续依据乘法算式编写乘法口诀提供了样例。

2.“一五得五”的口诀编写

依据“三五十五”口诀编写的经验，学生编制“一五得五”这句口诀。教师提问：这里的“得”是什么意思？学生回答是“等于”的意思，教师顺势提出：为什么这里要加“得”字？让学生读一读“一五五”，并与“三五十五”进行比较。学生发现如果口诀都是四个字，读起来就顺畅多了，因此，这里加了“得”字，既朗朗上口，又便于记忆。

學生依据“1×5”很自然地能够说出口诀“一五得五”，之后通过与“三五十五”的比较，发现不同点，经历乘法口诀编写规则的完善过程。

3.“二五一十”的口诀编写

在前测中发现，有学生把“二五一十”写成“二五得十”。教师在这里将这句口诀与“2×5=10”的读法进行比较，并提出疑问：口诀中“一十”的“一”可以去掉吗？让学生先读一读“二五十”感受一下，并与已经编制好的口诀（如三五十五、一五得五）进行比较，再把“二五得十”与“一五得五”进行比较，辨析“二五一十”与“二五得十”哪一句口诀更合理。学生发现，“十”是一个两位数，“五”是一个一位数，所以“一十”比“得十”更能够体现这一特点。

数学表达是一个不断完善、改进、规范与优化的过程，仔细分析不同的乘法口诀，可以体会这一过程。把“三五十五”作为乘法口诀的基本模型，“一五得五”和“二五一十”作为规范与优化的例子，能让学生感受到乘法口诀编写过程中的智慧。

（三）图式联想，自创乘法口诀

有了前面三句乘法口诀的创编与辨析，剩下的“5的乘法口诀”就让学生进行自主创编，并在创编的过程中进一步完善。

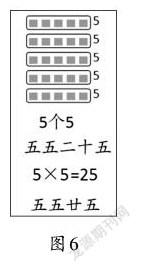
教师依次出示4个5相加和5个5相加的图式，让学生再次经历“数一数”“列一列”“算一算”与“编一编”的过程，层层递进构建起图式、乘法含义、乘法算式、乘法口诀之间的联系。在依据“5×5”编制乘法口诀“五五二十五”后，教师再次提出质疑：这句口诀有五个字，能不能把“十”去掉？教师结合口诀发展史和地方特色进行解释（如图6），并通过让学生反复朗读，体会这两种读法中哪一种更加适合于现在的应用。

很多学生虽然课前已经会背乘法口诀，但并不清楚乘法口诀的编写规律，因此，在学习口诀的过程中，要让学生追本溯源，理解乘法口诀的来源、编写规律等，以便更好地记忆口诀、运用口诀。

二、迁移类比，自主尝试创编乘法口诀

迁移类比是用熟悉的解决问题的方法去解决新问题的一种策略。通过上面的活动，学生掌握了解决这类问题的图式规则，可将这一规则迁移类比到4、3、2、1的口诀中。同时，学生看着口诀能联想到具体的含义、算式和结果等。

（一）模仿创编，丰富乘法口诀

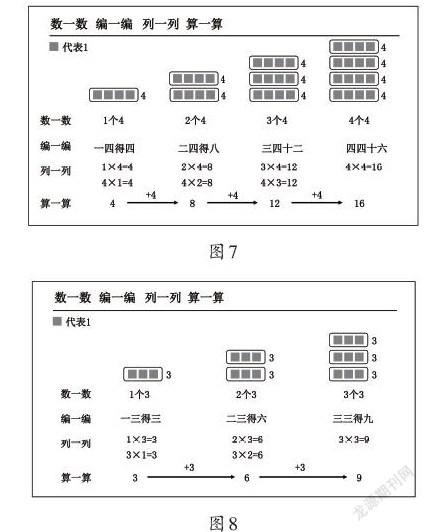
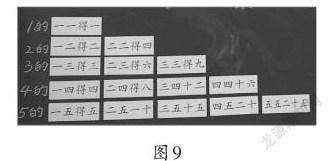
教师首先依次出示“1个4”“2个4”的图式，请学生猜测这是关于谁的口诀。当学生回答是关于“4的乘法口诀”后，教师追问：“‘一四得四’表示有几个4？‘二四得八’呢？”……教师接着依次出示“3个4相加”和“4个4相加”的图式，请学生依次用“数一数”“列一列”“算一算”“编一编”的方法得到“4的乘法口诀”（如图7）。用类似的方式，得到有关“3的乘法口诀”（如图8）。

（二）依据口诀，联想算式含义

教师让学生依据编写的经验，猜想2、1可能有怎样的乘法口诀，又是怎样的含义，以此检验学生对“乘法口诀”“乘法含义”与“乘法算式”之间沟通的能力。

教师提问：2的口诀有哪几句？根据学生的回答，依次追问：“一二得二”是什么意思？算式怎么列？“二二得四”的含义是什么？怎么列式？……接着用同样的方式学习“一一得一”。教师提问：“一一得一”能不能写出相应的加法算式？学生发现1个1可以用乘法算式表示出来，但无法用相应的加法算式表示，进一步体会乘法含义。

联想是一种重要的思维方式，当学生看到一句乘法口诀时，能否联想到相应的“乘法含义”与“乘法算式”，是后续应用“乘法口诀”进行计算的基础，更是训练学生联想思维的一个很好的载体。

（三）比较联系，发现口诀特征

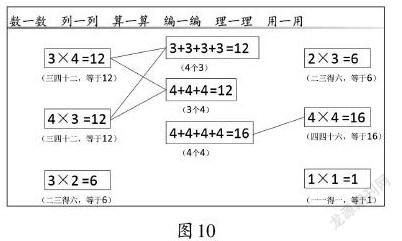
通过前面的学习，得到5以内的乘法口诀（如图9），教师提出问题：这些乘法口诀中，有哪些相同的地方？根据学生回答，进行归纳：①竖着看，每一列的第一个乘数相同;横着看，每一行的第二个乘数相同。②乘数一样，只有一个乘法算式的口诀：一一得一、二二得四、三三得九、四四十六、五五二十五。③积一样的口诀：一四得四和二二得四。

通过“理一理”这一数学活动，在变中找不变，发现5以内的乘法口诀的特征，为后续学习6～9的乘法口诀做铺垫。学生深刻地感受到，“乘法口诀”不仅仅只是一种记忆，它的内部有着很多规律与特征。

三、解决问题，逐步灵活应用乘法口诀

在通过以上活动得到5以内的乘法口诀并知道口诀中的一些规律、特征之后，还要学以致用，会用口诀熟练计算相关的乘法算式以及相应的变式。在解决问题的过程中，进一步加深对乘法口诀含义、算式、口诀之间联系的理解。

（一）题组练习，口诀应用变式

对于大的乘数在前的算式的计算，学生容易出错，因此教师设计了相应的题组练习。

教师用课件出示6道乘法算式：3×4、2×3、

4×3、4×4、3×2、1×1，请学生进行抢答。在抢答前，先让学生运用乘法口诀口算出结果。以“3×4”为例，引导学生这样说：三四十二，等于12。后面的算式都可以用这样的格式进行表达。在这一过程中，学生既巩固了口诀记忆，也加强了对口诀与算式之间联系的认识。

“表内乘法计算”是“乘法口诀”运用于乘法计算的第一阶段，首先要规范思路，看到“乘法算式”就能夠迅速联想到相应的“乘法口诀”，其次要简化表达，把算式的阅读与乘法口诀有机结合。

（二）联系加法，口诀意义回溯

有了用口诀口算乘法算式的经验后，教师出示加法算式“3+3+3+3”，学生自然而然地回答：三四十二，等于12。教师进一步追问：这是加法算式，怎么用了乘法口诀？这时学生会联想到“几个几相加”。之后教师又出示几组加法算式进行巩固练习。同数连加的算式，渗透了乘法含义，沟通了口诀、乘法含义、加法算式之间的联系。

（三）连线沟通，厘清内在联系

教师出示图10，提问：“‘3+3+3+3’可以改写成哪个乘法算式？”根据学生回答，在课件中连线展示。紧接着提问：“‘4+4+4’可以连线哪个乘法算式？”学生通过连线发现，“3+3+3+3”和“4+4+4”虽然一个表示4个3相加，一个表示3个4相加，但可以同时连3×4和4×3，用同一句口诀。而“4+4+4

+4”表示4个4相加，只能写出一个乘数相同的乘法算式。这一练习让学生进一步感受到乘数相同的乘法算式与乘数不同的乘法算式对应的加法算式的个数是不一样的。

回顾本节课的教学过程，以编制5以内的乘法口诀为主线，规范乘法口诀的编排流程，沟通乘法口诀与乘法含义、乘法算式、同数连加算式之间的联系。“乘法口诀”的结构虽然十分简单，但是它蕴含着我国古代劳动人民的智慧，教学中不仅是简单地记录乘法口诀，还要展现乘法口诀简化、优化与模型化的过程。

（1.浙江省杭州市春晖小学   311201    2.浙江省杭州市滨和小学   310051）