基于IMCKD和MCCNN的滚动轴承故障诊断方法
刘好博, 郝洪涛,2, 丁文捷
(1.宁夏大学 机械工程学院,银川 750021;2.宁夏智能装备CAE重点实验室,银川 750021)
滚动轴承作为机械设备中的易损部件,它的工作状态对设备的稳定性和使用寿命有重大影响。当轴承出现裂纹、点蚀等故障时,轻则使设备异常振动影响产品质量,重则可能导致整个设备损坏,甚至引起重大安全事故[1]。因此,对滚动轴承进行有效地故障诊断十分必要。
然而,滚动轴承故障诊断面临诸多棘手问题。一方面,受外界环境、设备的多源噪声干扰,使得信号信噪比低,故障特征微弱。另一方面,当滚动轴承出现局部损伤或缺陷时,在旋转过程中会引起高频脉冲响应,各组件的固有频率易被激起,导致部件振噪耦合。因此,如何有效增强滚动轴承微弱故障特征信息受到越来越多学者的关注[2-3]。
最大相关峭度解卷积(maximum correlation kurtosis deconvolution, MCKD)[4]以信号的最大相关峭度值为目标函数,可通过迭代方式实现解卷积运算,突出强背景噪声下故障信号中周期性冲击成分。Li等[5]利用MCKD的降噪特性,将其和经验小波变换(empirical wavelet transform, EWT)相结合,提出了基于MCKD和改进EWT的故障特征提取方法,并在轴承故障特征提取和增强方面得到验证。Hua等[6]将最大相关峭度解卷积和包络谱相结合来提取齿轮箱故障特征信息,成功实现了强噪声环境下齿轮箱故障模式识别。Wang等[7]利用最大相关峭度解卷积对故障信号进行降噪,并对所得信号做进一步经验模态分解来提取特征向量,最后结合支持向量机(support vector machine, SVM)成功实现了轴承复合故障的识别和分类。在已有的成功应用中,仍值得进一步探究的问题有:①MCKD的输入参数需要人工设置,只有适当选择滤波器长度参数L和解卷积周期参数T,才能保证算法的有效性;②人工提取故障特征较为困难,需要一定的先验知识,且诸如SVM的模式识别方法对复杂函数的表达能力有限,难以全面挖掘故障信号中内在的丰富信息,模型的泛化能力差。
深度学习作为人工智能领域一种新兴的关键技术,在计算机视觉[8]、语音识别[9]等领域已经取得显著成就。深度学习通过构建多隐含层的深层模型,能自适应提取更深层次的特征,表征数据与故障征兆之间复杂的非线性映射关系,减少对信号处理技术和专家先验知识的依赖。卷积神经网络(convolutional neural network, CNN)[10]作为一种典型的深度学习模型,其通过构建多层处理单元,以分布式方式逐层有监督的学习数据内在特征。与其他深度学习模型相比,CNN具有局部连接、权值共享和空间降采样的优势,这大大降低了网络复杂度和过拟合的风险,且在故障诊断领域取得了一定的成果。Ince等[11]将原始振动数据作为卷积神经网络的输入来进行电机的故障诊断,并验证了其有效性。Wang等[12]提出了由1-D和2-D卷积通道组成的多尺度卷积神经网络识别滚动轴承的工作状态。其中一维CNN用于学习原始振动数据相邻间隔的局部相关性,二维CNN用于学习原始振动数据不相邻间隔的局部相关性,诊断准确率得到了显著提高。李恒等[13]将短时傅里叶变换后的数据输入卷积神经网络中进行学习,提出一种基于短时傅里叶变换和卷积神经网络的故障诊断方法,实现了端到端的故障模式识别。尽管上述方法具有较强的特征学习能力,可以实现有效的故障诊断。但由于使用原始信号作为输入数据,模型对噪声具有很高的灵敏度,因此很难在强背景噪声干扰下拥有良好的表现。
为了克服强背景噪声下特征提取能力弱的问题,提出一种基于改进最大相关峭度解卷积和多通道卷积神经网络的滚动轴承故障诊断方法。该方法将原始信号作为输入,以解卷积信号的相关峭度为目标函数,采用萤火虫算法(firefly algorithm, FA)对MCKD的影响参数组合[L,T]进行并行寻优,以实现最优参数的自适应选取,提高对原始信号的滤波效果。然后利用多通道卷积神经网络特征学习的优势,充分学习滤波后信号中的故障特征信息,最终达到提高模型故障分类准确率和抗干扰能力的效果。
1 基于FA的MCKD
Yang等[14]作为一种高级启发式群体智能优化算法,它源于对自然界中萤火虫群体行为的模拟,具有较强的全局寻优能力,可用于对MCKD的滤波器长度参数L和解卷积周期参数T进行并行寻优,自适应地筛选滤波器长度参数L和解卷积周期参数T。
假设萤火虫当前的状态为X=[X1,X2,X3,…,XM],其中M为萤火虫种群规模,XM表示第M个萤火虫所处的位置,将[L,T]作为萤火虫的位置参数,即Xi=[Li,Ti](i=1,2,…,M),对信号做MCKD运算并计算解卷积信号的相关峭度值CK作为其发光亮度。则Xi处的发光亮度为
Ii=CK(Xi)
(1)
当解卷积信号中周期性冲击成分明显时,相关峭度值较大,则发光亮度较大,反之则较小。萤火虫通过比较彼此之间的发光亮度来决定自己的位置移动,遵循低亮度的萤火虫向高亮度的移动,而亮度最高的则随机移动。因此,解卷积信号相关峭度值CK最大化即为最终寻优目标。
MCKD滤波器长度参数L和解卷积周期参数T的具体优化步骤如下:
(1) 初始化萤火虫种群规模M,最大迭代次数Gmax,随机步长因子α等参数,并确定相关峭度值作为寻优过程中的目标函数;
(2) 每个萤火虫对应一组影响参数[Li,Ti],随机初始化M个萤火虫的位置,并计算各自相关峭度值作为自己的最大亮度;
(3) 根据萤火虫的位置参数对信号作MCKD运算,并计算每个萤火虫的Ii;
(4) 依照Ii大小确定萤火虫的移动方向;
(5) 更新萤火虫的位置参数[Li,Ti],并对这一代中最优个体的位置进行随机扰动;
(6) 循环迭代,转至步骤(3),直至迭代次数达到最大设定值,输出最佳影响参数组合[L,T]和相关峭度值CK。
2 多通道卷积神经网络
2.1 CNN及其特点
CNN是一种典型的前馈神经网络,其通过局部连接、权值共享和空间降采样来减少预处理量,自适应提取数据更深层次的特征。典型的CNN由输入层、输出层和多个隐含层构成,其中隐含层通常包含卷积层、池化层和全连接层,输入层和输出层是CNN的可视化层。
卷积层用于提取输入数据的特征,其内部包含多个特征图,每个特征图上的神经元节点又通过卷积核与先前层的特征图稀疏连接。每一个卷积核作用于局部感受野,通过设定的移动步长作用于全局感受野,完成对各输入特征图的卷积,提取局部特征。且卷积核作为媒介在同一输入特征图和输出特征图之间局部连接时共用一套权值。卷积过程可表示为
(2)

在每个卷积层之后,通常会连接一个激活层。目的是给神经网络模型引入非线性特征,使其可以逼近任意非线性函数。由于Sigmoid非线性激活函数存在梯度消失和计算成本等问题,因此在CNN中普遍使用整流线性单元(rectified linear units,ReLU)[15]。其函数表达如下
f(x)=max{0,x}
(3)
池化层用于减少输入特征图维度和网络参数,可有效防止过拟合和减少计算量。常用的池化类型有:最大池化、平均池化、全局平均池化。其中最大池化用于计算特征图中局部区域的最大值,是最常用的池化函数。其数学表达如下
(4)
批正则化(batch normalization,BN)层[16]是将输入数据转换成标准正态分布的操作,不仅解决了在训练过程中网络中间层数据分布发生改变的情况,在一定程度上可加快神经网络的收敛速度。在CNN中,批正则化层通常作用在激活层前。
通常在多个卷积和池化后添加全连接层和分类器。全连接层中的每个神经元与先前层的每个神经元进行全连接,用于对从原始数据中提取的特征进行整合,并输入到分类器中进行分类。在CNN中,常采用Softmax分类器对提取到的特征进行分类,估算样本属于不同种类的分类概率。Softmax回归的输出表达如下
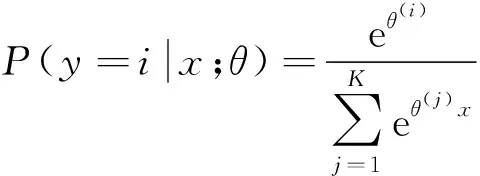
(5)
式中,θ(i)(1≤i≤k)为模型的参数,得到的P(y=i|x;θ)即为模型的诊断准确率。
2.2 MCCNN及其特点
CNN的性能与网络结构和卷积核的大小密切相关。在一定程度上,网络结构越深,非线性表达能力越强,但这也意味着需要更多的数据来训练大量的参数。此外,小卷积核可以提取数据的局部特征,而大卷积核则具有较大的感受野,可以捕获更多数据的全局特征[17]。作为一种折衷,大部分卷积神经网络使用中等大小的卷积核。如VGG-net[18]使用所有尺寸为3×3的卷积核,在Image-net数据集上具有一个良好的表现。但一维振动信号不同于二维图像,使用所有尺寸为 3×1的卷积核将增加网络计算量和过拟合度,使其很难训练,且小卷积核很容易受工业环境中高频噪声的干扰。
为了充分发挥CNN对信号特征提取的优势,提高模型的抗干扰能力,提出一种多通道卷积神经网络(multi-channel convolutional neural network, MCCNN)。与传统的CNN相比,MCCNN包含三个并行的卷积通道,且每个通道第一卷积层的卷积核尺寸不同,如图1所示。

图1 多通道卷积神经网络结构图
三个并行的卷积通道输入均为原始振动数据,在特征提取早期,每个通道彼此独立,经过四次卷积池化操作后,三个通道提取的特征在随后的分类阶段进行融合,用于最终的故障分类。最终提取到的特征可表示如下
F=[F1;F2;F3]
(6)
式中:F为连接层融合后的特征;F1、F2、F3分别为三个卷积通道提取到的特征。
MCCNN的训练目标是最小化神经网络的代价函数,使得真实值与预测值的误差最小。代价函数有多种,常见的有均方误差函数、交叉熵函数、负对数似然函数等[19]。由于交叉熵函数在梯度下降时可有效避免学习速率降低的问题,因此选择交叉熵作为代价函数来表达真实值与估计值的误差,其数学表达式为
L=-∑xp(x)lnq(x)
(7)
式中:p(x)表示样本真实类别;q(x)表示分类器输出的分类结果。
此外,使用ADAM[20]优化算法来训练MCCNN,确定网络各层神经元的权值和偏差。
3 故障诊断流程
基于IMCKD和MCCNN进行滚动轴承故障诊断的步骤为:数据划分、样本信号滤波处理、数据集构建、MCCNN构建与训练和滚动轴承智能故障诊断。
(1) 数据划分
采用数据增强技术对原始信号进行重叠采样。过程如图2所示。用等长度窗口对信号进行划分,当窗口移动步长小于单个样本长度时,样本之间有重叠,能够获取更多训练样本,以增强模型的表达能力。使用该方法,长度为Lsignal的信号被划分后的样本数量可表达如下
N=(Lsignal-lsample)/s
(8)
式中:lsample为单个样本的长度;s为窗口移动步长。

图2 数据划分
(2) 样本信号滤波处理
设定萤火虫算法的最大迭代次数Gmax=30,种群规模M=20,步长因子α=0.9,并行搜寻MCKD的滤波器长度参数L和解卷积周期参数T。萤火虫寻优后会得到一组最佳影响参数组合[L,T],利用参数优化后的MCKD算法对样本信号作滤波处理。
(3) 数据集构建
将所有的样本信号进行上述操作且进行归一化,构建数据集,并将数据集随机划分为训练集和测试集。
(4) MCCNN构建与训练
构建可行的MCCNN,随机初始化网络的权值和偏差,设定学习率、迭代次数等训练参数。以批量方式将训练集输入到MCCNN中,使用ADAM自适应学习率算法进行训练,并依据输出结果对网络参数进行调整,直到获得最优MCCNN。
(5) 滚动轴承智能故障诊断
通过测试集验证基于IMCKD和MCCNN的滚动轴承故障诊断方法的有效性。
4 故障信息采集试验与分析
MCCNN是在Tensorflow学习框架下使用Python3.7编写实现的,并在具有NVIDIA GPU和内核i7的Windows 10系统上运行。
4.1 设备
为验证提出方法对滚动轴承故障诊断的有效性,选用由美国SpectraQuest公司生产的机械故障综合模拟器(machinery fault simulator, MFS)来采集不同工作状态下的滚动轴承振动数据,试验装置如图3所示。

图3 机械故障综合模拟器
试验在远离电机一侧的滚动轴承上进行,分别对滚动轴承的内圈故障、滚动体故障和外圈故障进行了模拟。两个相互垂直的加速度传感器安装在测试轴承的轴承座上,用于采集竖直和水平方向轴承正常状态和3种故障状态的振动信号。试验过程中的参数设置如表1所示。

表1 试验参数设置
4.2 数据采集
用来模拟轴承故障的轴承型号为ER-12K,其结构参数如表2所示。

表2 滚动轴承结构参数
将竖直方向传感器获得的振动信号作为本次试验的有用数据,对各状态下采集到的振动信号进行处理。其中窗口长度为2 000个采样点,移动步长为300,每种状态下得到4 000个样本,随机选取3 750个样本作为训练数据,其余作为测试数据。数据集详细信息如表3所示。
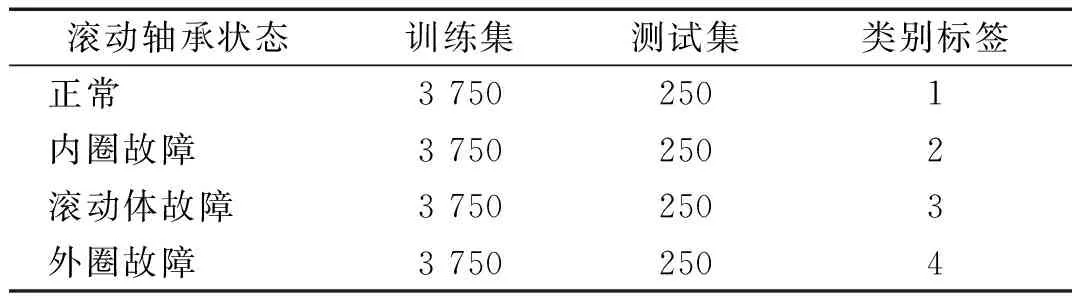
表3 试验数据集的描述
4.3 MCCNN测试模型
适当的CNN结构和网络参数在很大程度上取决于经验。卷积层的数目、卷积核的大小、池化层的大小、全连接层的神经元数目等网络参数都与CNN的性能紧密相关。MCCNN具有三通道CNN结构且读取数据相同,每个通道由四个卷积层和池化层交替进行,但第一卷积层的卷积核尺寸不同,三个通道的CNN提取的特征在随后的融合层进行融合,最后全连接层整合特征信息并经Softmax分类器输出识别结果。经过反复试验调整,得到的MCCNN主要结构和参数如表4所示。其中S表示卷积核大小;F表示卷积核数目;Strides表示卷积核移动步长;K表示池化层池化带大小;Dropout表示以一定概率将网络中的部分神经元随机置零,可在一定程度上防止网络过拟合;此外,卷积层采用零填充方法在输入矩阵的边缘上补零,以避免尺寸的变化,而卷积层和池化层之间都存在批正则化层和激活层。

表4 MCCNN测试模型主要结构参数
4.4 结果与分析
4.4.1 试验结果
为了评估提出方法的有效性,使用准确率[21]作为评估指标。对于多类别分类的故障诊断问题,准确率表示在测试集的预测结果中,模型正确预测的样本数占总样本数的百分比,是衡量模型性能的综合指标。
某一外圈故障的滚动轴承振动加速度信号如图4所示。利用萤火虫算法对MCKD的影响参数进行寻优,解卷积信号的相关峭度值随种群进化代数变化的关系曲线如图5(a)所示,相关峭度最大值出现在第28代,搜寻到的最佳影响参数组合[L,T]为[325,135]。设定MCKD算法的滤波器长度为325,解卷积信号周期为135,对故障信号进行处理,得到的时域滤波结果如图5(b)所示。相比原始故障信号,滤波后的信号变得干净且周期性冲击成分更为明显。

图4 轴承外圈故障振动加速度信号

(a) 相关峭度值随进化代数变化的关系曲线
为了验证MCKD影响参数经萤火虫算法自适应寻优后滤波结果的可靠性,对图4所示信号施加高斯白噪声使信号信噪比为-10 dB,经萤火虫算法搜寻到的最佳影响参数组合为[320,135],随机更改最佳影响参数组合中的一个参数,得到参数组合1[305,135]和参数组合2[325,115],并利用上述三种影响参数的MCKD对故障信号进行滤波处理。理想情况下滤波后信号的信噪比应与添加噪声时给定的信噪比接近,表明恰好滤除了添加的噪声[22]。由表5可知,经参数组合1和参数组合2的MCKD滤波后信号的信噪比均增加,表明其对信号欠滤波,未能有效滤除噪声。综上所述,随机选择MCKD的影响参数滤波效果较差,利用萤火虫算法对影响参数进行寻优,可有效避免人工设定时主观因素的影响,提高信号的滤波效果。

表5 滤波前后信号信噪比
表6总结了卷积通道和第一卷积层卷积核的尺寸对模型精度的影响。为了消除偶然误差的影响,每种结构模型各进行了10次试验,将10次试验结果的平均值作为该结构模型分类性能的评估指标。可以看出,由于传统小卷积核增加了网络计算量和过拟合度,CNN1*3模型的平均故障识别率仅为87.49%,且随着卷积核尺寸的增大,识别率显著提高,标准差更小。此外,两通道卷积结构模型的故障识别率均高于单通道卷积结构模型。而MCCNN在迭代到25代时,平均故障识别率可达99.65%,当迭代到30代时,平均故障识别率已达99.78%,进一步提高了卷积神经网络的分类精度,且故障诊断稳定性明显优于其它结构模型。相比之下,因学习到的特征单一,同种卷积核尺寸的三通道卷积结构模型的故障识别率均低于MCCNN,且由于CNN1*3+CNN2*3+CNN3*3结构模型增加了网络计算量,其故障识别率反而低于两通道卷积结构模型。表7为不同模型的主要结构参数。

表6 不同结构模型性能比较

表7 不同结构模型主要参数
分别将原始数据集和经IMCKD方法处理后的数据集作为输入,将提出的MCCNN方法与DNN(deep neural networks)及文献[17]提出的WDCNN(deep convolutional neural networks with wide first-layer kernel)所实现的滚动轴承故障分类准确率进行了比较,结果如表8所示。其中DNN结构为2000-200-100-50-4,激活函数为ReLU。每种方法各进行了10次试验,将10次试验结果的平均值作为该方法分类性能的评估指标。可以看出,即使未经IMCKD方法处理,MCCNN的平均故障分类准确率仍高达99.78%,明显优于DNN、IMCKD+DNN、WDCNN和IMCKD+WDCNN,而且分类性能稳定,表现为多次试验得到的评估指标的标准差更小。经IMCKD方法处理后,三种方法的故障分类准确率均有所提高,其中IMCKD+MCCNN方法分类性能最为突出,诊断结果最稳定。原因在于经过IMCKD算法处理后有效突出了原始信号中周期性冲击成分,且不同尺寸卷积核进行特征提取,保留了信号的全局和局部信息,从而提高了MCCNN的特征学习能力。

表8 不同方法性能比较
t-SNE[23]是一种非线性降维算法,用于可视化高维数据。为进一步验证提出方法对不同特征类别的分类能力,将t-SNE降维算法用于可视化神经网络学习到的特征分布,降维后的二维散点图如图6所示。

图6 样本特征可视化
可以看出原始数据具有较大的冗余性,以至于很难区分其类别。经特征提取后,DNN表现较差,未能成功区分开各类样本。WDCNN虽能使样本特征各自聚拢,但3、4类样本仍具有个别交叉的现象。而经MCCNN全连接层对特征进行整合处理后,可以完全区分出四类样本,且类间距较大,特征可分性较好,显示了该方法强大的特征学习能力。
为了进一步验证IMCKD+MCCNN方法在不同噪声环境下的抗干扰能力,将测试集与不同强度的高斯白噪声相加,获得信噪比为-4 dB~4 dB的复合噪声信号,然后经IMCKD算法处理后用其分别对各个模型的分类性能进行了10次测试,测试均值和标准差的结果如表9所示。可以看出,在低强度噪声干扰下,IMCKD+MCCNN和IMCKD+WDCNN方法的分类精度都较理想,而IMCKD+DNN则表现较差。随着噪声强度的增强,所有方法的分类精度均有所下降,其中IMCKD+DNN的分类精度显著下降,在信号信噪比为-4 dB时,分类精度仅为65.44%。而与抗噪性较强的IMCKD+WDCNN相比,IMCKD+MCCNN不仅性能更优,即使信号信噪比为-4 dB,仍具有92.19%的分类精度,而且分类更稳定。综上所述,IMCKD+MCCNN方法在强背景噪声干扰下表现良好,具有较强的抗干扰能力。

表9 不同强度噪声下不同模型的分类精度
4.4.2 模型泛化能力验证
为了进一步验证IMCKD+MCCNN方法的泛化能力,在不同工况下进行故障诊断,新鲜数据样本如表10所示。

表10 不同工况下的数据集
每种故障类型在转速1 662 r/min和1 797 r/min下分别选取2 500个训练样本,而在转速1 902 r/min下分别选取300个测试样本进行试验。其中DNN和WDCNN的输入为未经IMCKD方法处理的原始数据,每种方法均进行了10次试验,将试验结果的平均值作为该方法的分类性能评估指标。
滚动轴承故障识别试验表明:
(1) 在迭代次数较少的情况下,IMCKD+MCCNN方法具有更快的收敛性和稳定的分类精度(图7),当迭代到16代时分类精度可达97.15%,迭代到80代时已达到99.9%的分类精度。与此同时,当迭代到16代时,WDCNN的分类精度仅为66.55%,DNN也仅为54.65%;
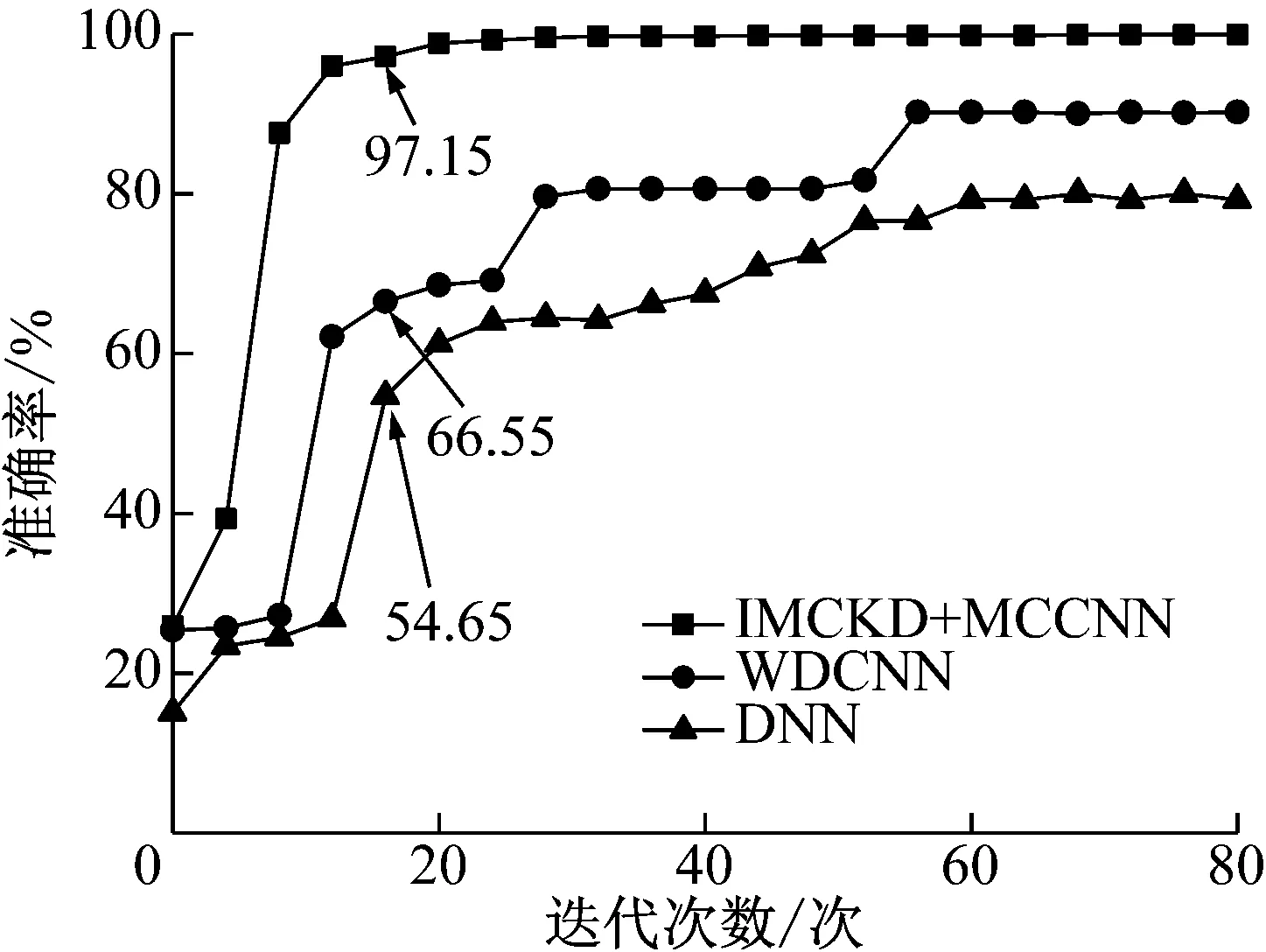
图7 不同工况下准确率
(2) 随着迭代次数的增加,WDCNN和DNN的分类精度呈现缓慢提升和局部突增的特点,当迭代到80代时,分类精度分别为90.25%和79.25%;
(3) 以标准差作为评估指标,IMCKD+DCCNN方法明显优于WDCNN和DNN两种方法(表11),诊断结果更稳定,泛化能力突出。

表11 不同工况下性能比较
5 结 论
基于改进最大相关峭度解卷积和多通道卷积神经网络的故障诊断方法具有两个主要特征,即数据自适应降噪和多通道特征学习。萤火虫算法并行搜寻MCKD的影响参数组合[L,T],利用参数优化后的MCKD对样本信号作滤波处理,适合构建冲击成分突出的数据集。多通道卷积神经网路结构中,三个通道的第一卷层分别采用不同尺寸卷积核,可分别提取数据的局部和全局特征,有效地提高了模型的故障分类精度和抗干扰能力。试验表明:
(1) 本文提出的基于IMCKD和MCCNN的故障诊断方法可对原始振动信号进行自适应处理,实现了滚动轴承的智能化故障诊断。
(2) 作为一种群体智能寻优算法,FA优化了MCKD影响参数选择的问题,提高了信号的滤波效果。
(3) 与传统CNN相比,构建的MCCNN进一步提升了网络提取状态特征的能力。
(4) 嘈杂的环境噪声严重影响了诊断模型的分类精度,IMCKD+DCCNN方法具有较好的抗干扰能力,即使在信噪比为-4 dB时,仍具有90%以上的故障分类精度。
(5) IMCKD+DCCNN方法具有较好的泛化能力和稳定性,在变工况下可以实现高达99.18%的故障分类精度。

