基于能量变分原理的梁-圆柱壳耦合系统振动特性分析

聂 睿， 李天匀， 朱 翔， 陈 旭

(1.华中科技大学 船舶与海洋工程学院，武汉 430074； 2.高新船舶与深海开发装备协同创新中心，上海 200240；3.船舶与海洋水动力湖北省重点实验室，武汉 430074)

以圆柱壳为主体的结构广泛存在于船舶与海洋工程、航空航天工程等领域中。其振动特性被国内外学者进行了广泛研究。受螺旋桨脉动力激励而产生的推进轴系-艇体整体结构振动是近年来水下航行器振动特性研究重点。推进轴系和艇体会相互传递振动，存在着明显耦合效应，建立两者耦合模型进行振动特性计算十分必要。但是在以往工作中，水下航行器推进轴系与壳体往往不考虑彼此的耦合作用，仅仅只探讨了隔离后轴系或壳体的振动问题[1-5]。如欲对轴-艇耦合系统的振动特性进行更全面分析，对组合结构振动这类问题开展更深入的研究势在必行。

对于组合结构，通常先将整个结构划分成多个子结构，再利用结构之间的连续协调条件体现结构间耦合作用。周海军等[6]利用改进傅里叶级数方法和波传播法分别求取了梁和圆柱壳的导纳，再利用阻抗综合法，建立了耦合计算模型。Qu等[7]采用广义变分法模拟梁、壳等结构单元，再基于Hamilton原理，计算了梁-球壳-柱壳组合结构振动响应。郭亮等[8]采用解析法对锥柱组合壳结构及多跨梁结构分别建模，并在轴承处建立横向连续条件，形成了有效的系统横向振动解析求解模型。李攀硕[9]分别利用解析法和有限元法计算子结构导纳，再通过频响函数综合法建立了轴与加筋壳体的耦合系统模型。Merz等[10]采用有限元和边界元方法建立水下加筋壳体模型，并通过简化的弹簧阻尼系统与用杆结构模拟的推进轴系耦合，计算了系统振动与声特性。

总的来说，已有文献中轴-艇耦合系统振动分析方法主要有数值法和解析法两种。有限元等数值方法可以用于分析各类耦合系统结构振动问题，但它们难以从机理上对系统振动行为提供合理解释。而解析法能给出较精准的解析结果，易于从机理上解释某些研究现象，但其往往又存在求解范围有限的缺点。而实际应用中存在大量复杂的边界约束，解析法针对不同边界需要配置不同位移函数和边值条件，难以建立统一的动力学分析模型。

Rayleigh-Ritz法作为一种基于能量变分原理的(近似)解析法，由于其假定振型函数满足结构位移边界条件和振动方程，由此得到的函数组合往往接近真实振型，因此有很高精度；同时，由于假定振型函数之间具有正交性，实际运算成本极低。此外，Rayleigh-Ritz法还十分容易处理附加质量或附加刚度。只需添加附加动能项或附加应变能项，即可在不改变结构原振型函数的前提下，求取新系统振动特性。但传统Rayleigh-Ritz 法的限制是：对复杂边界条件，难以选取恰当的假设振型函数。Li[11]提出了一种改进傅里叶级数，该级数通过在传统傅里叶级数增加辅助多项式函数，保证了梁结构在边界上的连续性，结合两类弹簧模拟一般边界的思想，成功建立了梁的自由振动计算模型。随后，国内外学者借鉴该研究思路，结合Rayleigh-Ritz法，研究了梁、板、壳等各类结构的振动特性[12-15]。这些研究证明，引入改进傅里叶级数的Rayleigh-Ritz法，在面对复杂边界条件时，可构建准确统一的分析模型。

当对艇体中段进行截断处理后，轴-艇耦合结构可简化为梁-圆柱壳耦合模型[16]。在对轴-艇系统进行合理简化后，本文将以梁-圆柱壳结构为研究对象，基于能量变分原理，采用改进傅里叶级数统一描述梁结构和圆柱壳结构的振动位移；通过人工约束弹簧组模拟各类边界条件，耦合弹簧组来满足梁壳之间的连续条件，建立了梁-圆柱壳耦合系统振动计算模型。如前文所述，本文方法是对Rayleigh-Ritz 法的改进，故所得计算模型不仅可用于圆柱壳取各类经典边界条件下的梁-圆柱壳耦合结构，同时由于级数良好的收敛性亦只需极低运算成本即获得准确结果。通过与有限元软件的计算结果对比，验证了本文计算模型正确性。最后，分析了系统在部分参数改变时，振动响应性能的变化规律。

1 梁-圆柱壳耦合系统振动计算模型

1.1 模型描述

当进行截断处理后，轴-艇耦合系统可合理简化为梁-圆柱壳结构。即推进轴系可简化为带集中质量点的弹性梁，艇体可简化为两端受弹簧约束的圆柱壳，中间轴承等结构可简化为连接梁结构与壳结构的耦合弹簧组。

梁-圆柱壳耦合模型如图1所示，全局坐标系为直角坐标系O-xyz，坐标原点O位于梁结构左端点处；圆柱壳的长度和截面半径分别为L和R，壳体中面轴向位移、周向位移、径向位移及绕y轴转角分别为ucy、vcy、cy、βcy(βcy=∂cy/∂x)；梁通过两处节点与圆柱壳连接，每段长度分别为l1和l2，梁的自由端有一附加集中质量点，其质量为m；kL和kR分别为左连接点与右连接点的空间点对点耦合弹簧组(由三向线位移弹簧kx、ky、kz和两向转角弹簧Ky、Kz构成)；圆柱壳两端引入两组连续线分布的约束弹簧用于模拟各类边界(由三种位移弹簧ku、kv、k和一种转角弹簧Kβ构成)；fx、fy、fz为作用在质量点处的简谐激励力。

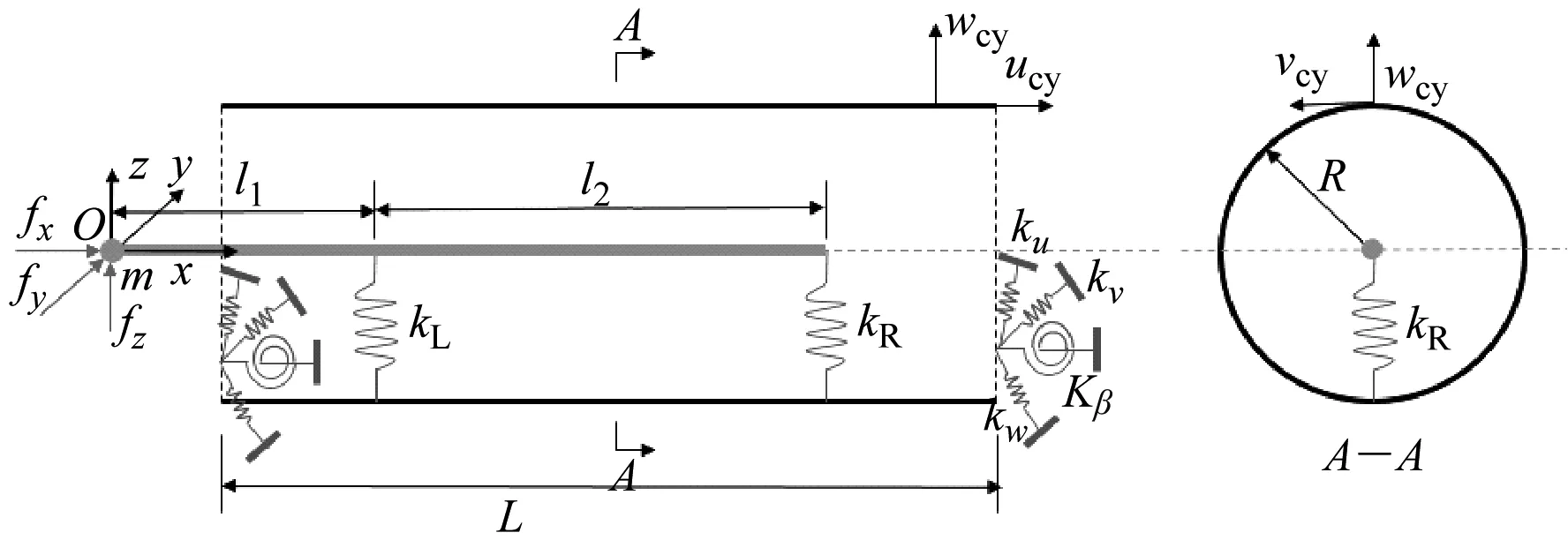
图1 梁-圆柱壳耦合模型

1.2 理论推导

如前文所述，与直接求解结构控制微分方程的方法不同，本文将基于能量变分原理建立梁-圆柱壳耦合模型。耦合结构能量泛函Π的形式如下

Π=Tb-Ub+b+Tcy-Ucy-Uc

(1)

式中:Tb为梁结构的总动能;Ub为梁结构的总势能;b为梁结构上外部激励力的外力功；Tcy为圆柱壳结构的总动能;Ucy为圆柱壳结构的总势能；Uc为结构耦合弹簧储存的弹性势能。

本文计算模型中梁结构为含集中质量点的弹性欧拉梁，其自身局部坐标系为xbybzb，坐标原点Ob位于梁左端，如图2所示。

图2 含集中质量点的梁结构

梁结构的总动能Tb由梁结构自身动能Tb,s和集中质量点的动能Tb,m构成

Tb=Tb，s+Tb，m

(2)

式中:ub，vb和b分别为梁结构在纵向(x)，横向(y)和垂向(z)的位移;ρb和Ab分别为梁的密度和截面面积;m为集中质量点的质量。集中质量点附加在梁结构左端面上，即梁结构坐标系中原点处。

由于本文计算模型中梁结构无外部约束，其势能Ub仅由自身应变势能构成，形式如下

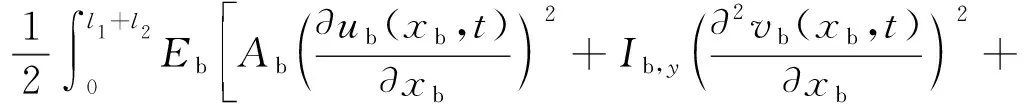
(3)

式中:Eb为梁材料的杨氏模量;Ib,y和Ib,z是梁的截面惯性矩。

集中质量点处作用有纵向、横向及垂向三个方向的简谐点激励力，由此产生的外力功b如下

b=fxub(xb,t)|xb=0+fyvb(xb,t)|xb=0+

fzb(xb,t)|xb=0

(4)

圆柱壳结构采用柱坐标系(R,θ,xcy)，xcy和θ分别代表轴向和周向坐标,坐标原点Ocy位于圆柱壳左端面圆心处。圆柱壳结构如图3所示。

图3 圆柱壳结构示意图

采用Ressiner薄壳理论计算圆柱壳的动能与应变能。动能Tcy具体形式如下

(5)

式中:ρcy为壳体密度;hcy为壳体厚度。

在圆柱壳两端引入两组沿端面圆周方向均匀分布的线性弹簧组用于模拟各类边界条件。因此，圆柱壳的总势能Ucy由自身应变能Ucy,p和存储在边界弹簧的弹性势能Ucy,e组成。具体计算形式如下

Ucy=Ucy,p+Ucy,e

(6)

式中:Ecy和μcy分别为圆柱壳的杨氏模量和泊松比;ku0，kv0，k0和Kβ0为圆柱壳左端约束弹簧;ku1，kv1，k1和Kβ1为圆柱壳右端约束弹簧。连续线分布的位移弹簧和转角弹簧的单位分别为N/m2和N/(rad·m)。

梁结构和圆柱壳结构将通过分布弹簧系统实现耦合。每对耦合节点之间的耦合弹簧组均包含纵(x)向、横(y)向和垂(z)向三种线位移弹簧与y向及z向两种转角弹簧。圆柱壳的振动位移分量将从局部柱坐标转换到全局笛卡尔坐标下，以便构造耦合弹簧组的能量泛函。梁结构和圆柱壳结构的振动位移如图4所示。

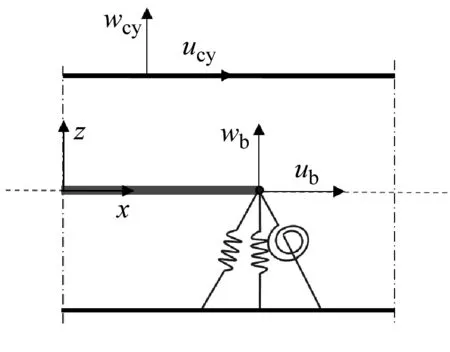
图4 梁和圆柱壳的振动位移

vcy=vcycosθ-cysinθ,cy=cycosθ+vcysinθ

(7)

式中，vcy和cy为圆柱壳结构转化到全局坐标系下的振动线位移分量。

通常，薄壳理论在解决壳体问题时，壳体模型仅考虑三向线位移和绕y轴旋转位移。但本文工作中为保证梁、壳结构的耦合振动分量数目相当，需要再加入绕z轴旋转位移αcy。引入额外旋转位移并进行转化后的形式如下

Rotcy,y=βcycosθ-αcysinθ

Rotcy,z=αcycosθ+βcysinθ

(8)

式中，Rotcy,y和Rotcy,z为圆柱壳结构转化到全局坐标系下的旋转位移分量。

如前文所述，本文计算模型含kL、kR两组梁壳耦合弹簧组。耦合弹簧存储的弹性势能Uc具体形式如下：

Uc=Uc,L+Uc,R

(9)

式中:Uc,L为左耦合弹簧组储存的弹性势能;kL,x，kL,y和kL,z分别代表x向，y向和z向的线位移耦合弹簧;KL,y和KL,z分别代表y向和z向的旋转位移耦合弹簧;(xL，θL)为左耦合弹簧组上圆柱壳耦合节点在柱坐标系上的位置坐标。下标R代表右耦合弹簧组对应的变量，故不赘述。

本文将引入改进傅里叶级数作为梁结构振动位移函数及圆柱壳结构轴向振动位移函数。同时，由于完整的圆柱壳拥有轴对称外形，其周向振动位移函数可由传统的两组单傅里叶级数描述。具体形式如下。

梁结构：

(10)

式中:Mb为位移函数的截断项数;Am,u和Bl,u是梁轴向位移容许函数中的未知傅里叶系数;eiωt被作为时间简谐因子引入来描述梁在不同时刻的位移;Am,v、Bl,v、Am,和Bl,是梁横向及垂向位移容许函数中的未知傅里叶系数。式(10)中的位移容许函数即为一种改进傅里叶级数，其中，λmb=mπx/(l1+l2)，λlb=lπx/(l1+l2)。它在传统的单余弦傅里叶级数基础上引入辅助正弦函数，使得容许函数满足轴向振动位移一阶导数或弯曲振动位移三阶导数在梁上的任意一点存在且连续，保证满足位移边界条件，同时加速了级数自身的收敛速度。

壳结构：

(11)

式中:Ncy、Mcy为位移函数截断项数;Amn等为未知傅里叶系数，λmcy=mπx/L，λlcy=lπx/L。

将式(1)～(11)联立，并根据最小势能原理，对能量泛函求取极值

(12)

式中，q为未知系数向量，q=[Am,u，Bl,u，…，Amn，al，…，Cmn，cl]。

最终得到的梁-圆柱壳耦合系统振动方程组矩阵化形式如下

([K]-ω2[M]){q}={F}

(13)

式中:[K]和[M]分别为耦合系统的刚度矩阵和质量矩阵;ω为圆频率;{F}为集中质量点处激励力的广义力向量。广义力向量取0时，亦可由式(13)求取系统的固有振动特性。

2 计算模型验证

为验证本文方法收敛性和计算模型准确性，下面将从傅里叶级数的截断项数出发，分析方法收敛性。同时，将本文计算模型计算结果与有限元软件计算结果进行比对，验证本文计算模型正确性。有限元模型共有31 566个单元。其中，壳单元31 400个，梁单元165个，质量点单元1个。

本文计算模型如前文所述，具体参数如表1所示。

表1 耦合模型参数

2.1 傅里叶级数截断项数收敛性

改进傅里叶级数的截断项数对计算结果精度有直接影响，其展开的数目越多，计算结果越趋于真实值，但过大的截断项数会降低求解效率。一般来说，截断项数达到一定值后，计算结果即可稳定(收敛)。本文以圆柱壳为自由边界条件(壳体两端约束弹簧组取值为0)的梁-圆柱壳模型为例，探讨计算结果收敛性随Mb、Mcy的变化。而圆柱壳周向截断数Ncy并不影响计算结果的收敛，仅仅会影响固定频率范围内结果是否会缺少某些模态。

验证模型参数见表1，Ncy=6，圆柱壳上的连接点为(xL，θL)=(0.5，π), (xR，θR)=(1.5，π)，梁的连接点为xb=l1和xb=l1+l2处。前8阶固有频率随截断项数Mb、Mcy的变化结果如表2所示。

表2 固有频率与截断项数关系

从表2可以看出，随着截断项数的增加，本文方法的计算结果很快就趋于收敛了，而与有限元法(finite element method,FEM)软件计算结果的对比证明了本文方法有很高精度。综合计算成本和精度，本文其余计算工作均取截断项数为10。

2.2 弹簧模拟经典边界条件

如前所述，本文采用两类弹簧模拟圆柱壳边界。弹簧刚度增大，储存的弹性势能也越大，圆柱壳边界处约束越强。但由刚度增大而产生的边界约束效应必定会趋于完全约束(位移或转角)。因此，取值达到一定大小的弹簧组可以用于模拟各类经典边界，例如固支边界即应为所有弹簧组取足够大值。下面将验证该假设。

仍取前文计算模型，但假定ku0、kv0、k0、Kβ0值取0，ku1、kv1、k1、Kβ1值取Q。显然，此时耦合模型圆柱壳左端边界条件仍为自由。图5将显示耦合系统计算模型固有频率随弹簧刚度取值Q的变化关系。

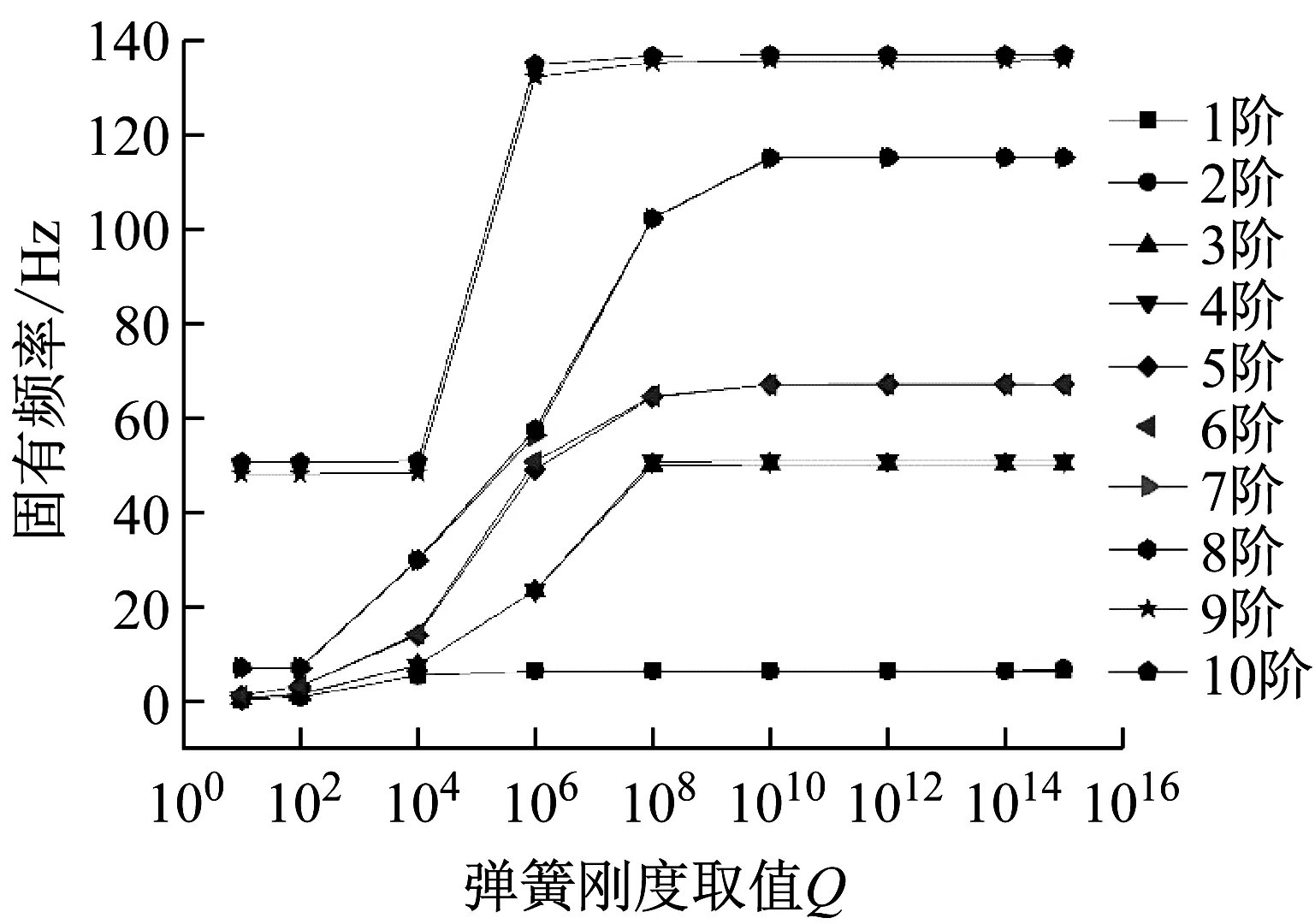
图5 边界弹簧组刚度取值Q对左端自由系统固有频率影响

从图5可知，耦合计算模型的前10阶固有频率随弹簧刚度增加都有着明显的“缓慢增加—快速增加—稳定不变”趋势，这证明了前文弹簧刚度收敛性假设正确可靠。此外，虽然不同阶固有频率的曲线变化规律略有不同，但在刚度值取1×1012左右均可以达到稳定。因此，本文其余工作均认为弹簧组刚度值取1×1012时，其对应方向上的壳体位移或转动为完全约束。由于本文计算模型在y(横)和z(垂)向是基本对称的，因此前10阶固有频率为两两一组，成对出现。

下面假定ku0、kv0、k0取值为Q，Kβ0为0，ku1、kv1、k1、Kβ1取值为1×1012。此时，圆柱壳右端所有位移均被完全约束，即对应固支条件。图6为此条件下耦合系统计算模型固有频率随弹簧刚度取值Q的变化关系。

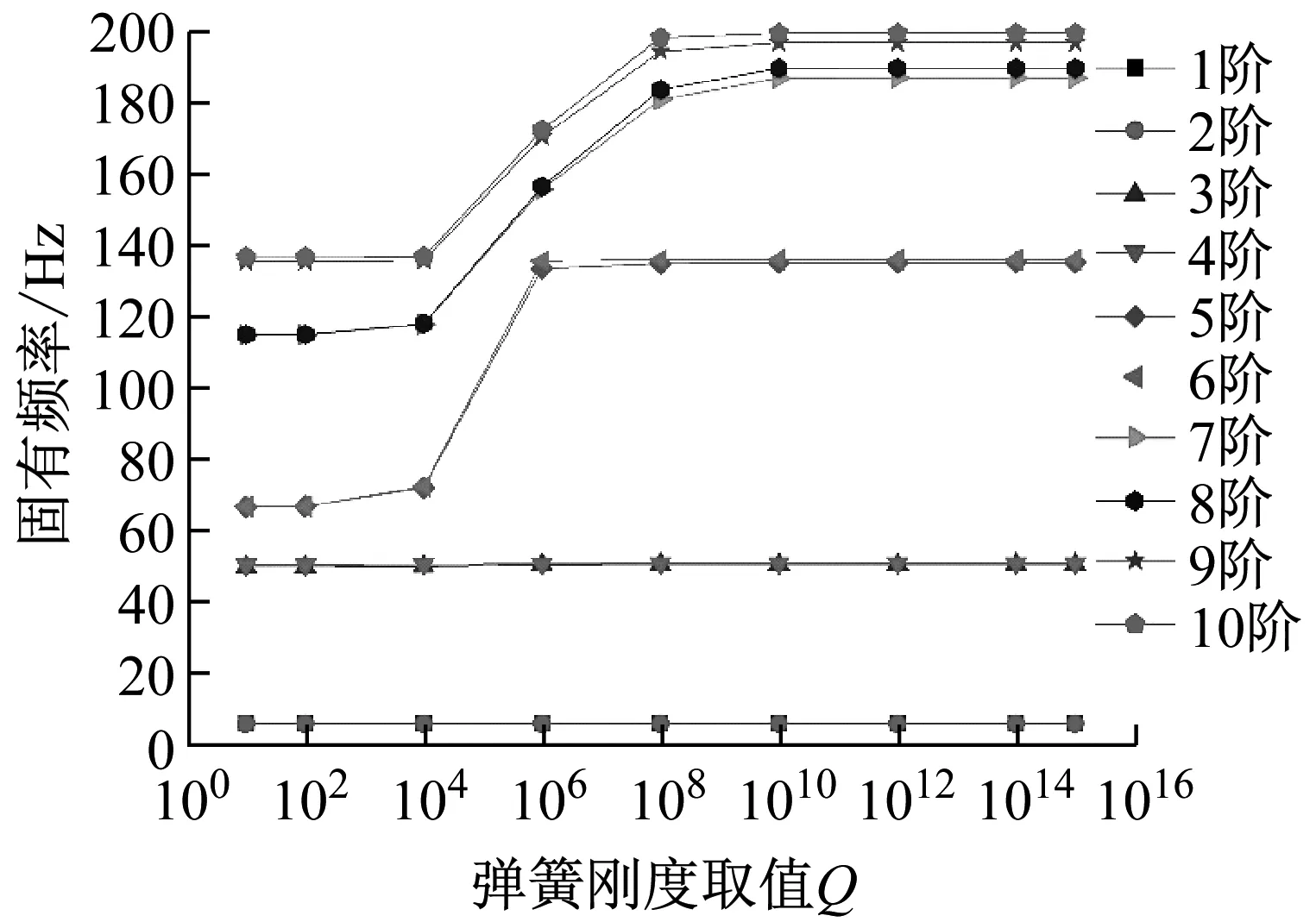
图6 边界弹簧组刚度取值Q对右端固支系统固有频率影响

从图6可以看出，在右端为固支条件时，增加圆柱壳左端线弹簧组的刚度，耦合系统固有频率也有类似的规律，弹簧刚度取值达到1×1012左右也趋于收敛。对应地，ku0、kv0、k0取1×1012且Kβ0取0，这一条件下，圆柱壳左端应视为简支边界条件。为进一步证明该假设的正确性，下面将这两种边界组合下的耦合系统固有频率计算值与有限元计算结果进行对比。结果如表3所示。

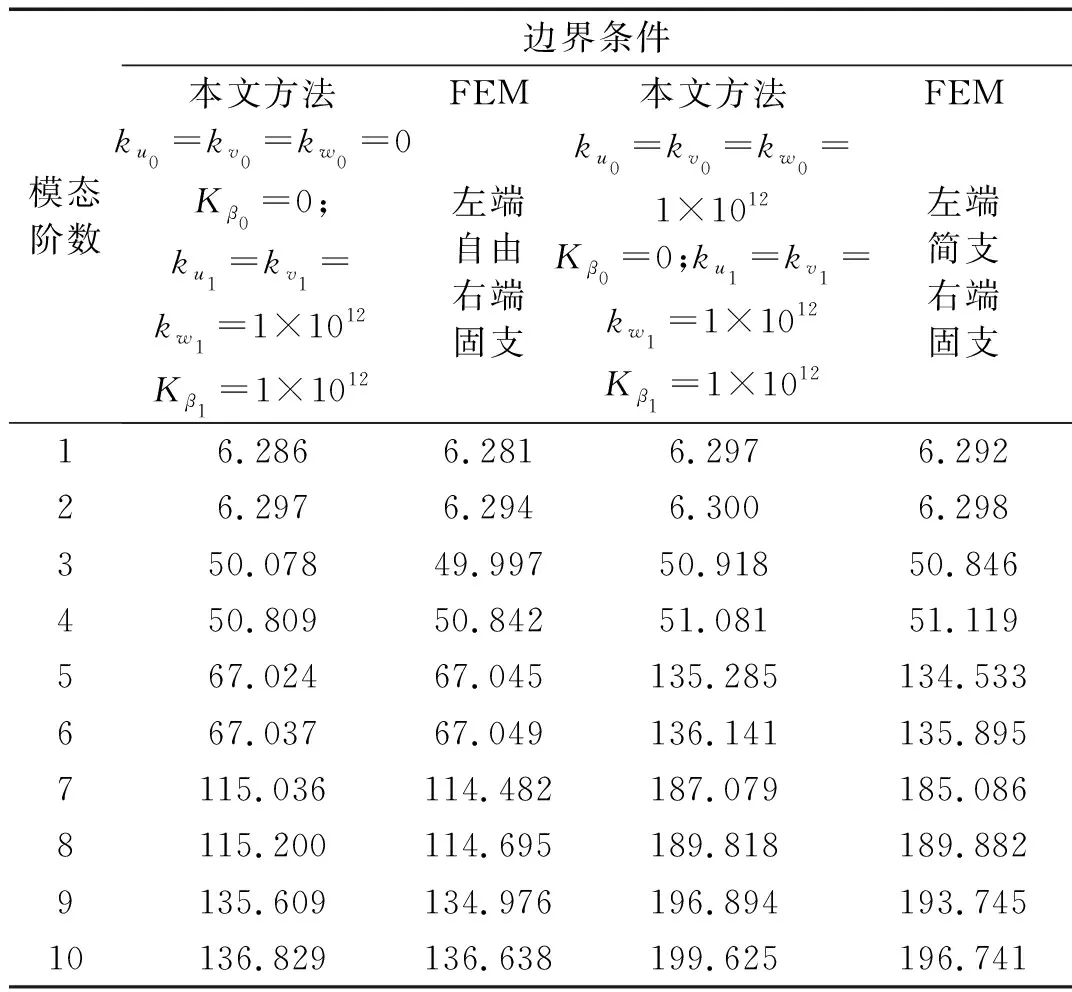
表3 本文方法计算结果与有限元结果对比

从表3的结果可以看出，本文方法和FEM计算结果十分接近，使用弹簧模拟边界的计算方法是正确可靠的。

2.3 计算模型正确性

在截断项数收敛性和弹簧刚度收敛性的探讨中，本文计算模型正确性已经从固有频率的比对中得到了初步验证。下面将进一步从对应模态振型及受迫振动响应的对比角度出发，验证本文计算模型正确性。

这里的验证模型取圆柱壳边界条件为简支-简支组合，其余参数保持不变。首先，对比梁结构z(垂)向振动的前5阶模态振型，结果如表4所示。

从表4可以看出，本文计算模型的梁结构z向振动前2阶模态，圆柱壳基本可视为刚体结构，不参与系统的振动。进一步观察得知，这2阶模态中，耦合点处于梁结构振型的不动点处，因此梁结构和圆柱壳结构难以通过耦合点进行振动传递。这也可以说明图6中，为何圆柱壳约束增强，但耦合系统前4阶(包括2阶垂向和2阶横向)振动的固有频率几乎没有变化。因为此时梁结构与圆柱壳结构可以视为解耦状态，圆柱壳可等效为刚性基础，其约束的增强并不能对系统产生明显影响。而后面的模态中，圆柱壳结构参与了整个系统的振动，因此其约束的增强会使得整个系统势能增加，固有频率也会随之增大。

然后，对比本文方法和FEM的受迫振动响应。在集中质量点处加z向单位幅值激励力，扫频范围为1～200 Hz，提取梁结构在质量点、左耦合点和右耦合点处的z向位移响应及壳结构在左耦合点和右耦合点处的z向位移响应。取参考位移A0=1×10-12m，A为提取点的z向位移响应幅值，则振动位移级响应为P=20lg(A/A0)。

从图7可以看出，本文计算模型与FEM软件计算结果十分吻合，这进一步验证本文方法的正确性。在190 Hz附近两种方法得到的位移级响应峰值位置存在微小偏差，表明两者计算得到的系统固有频率存在差别，这也与表3中内容相符。

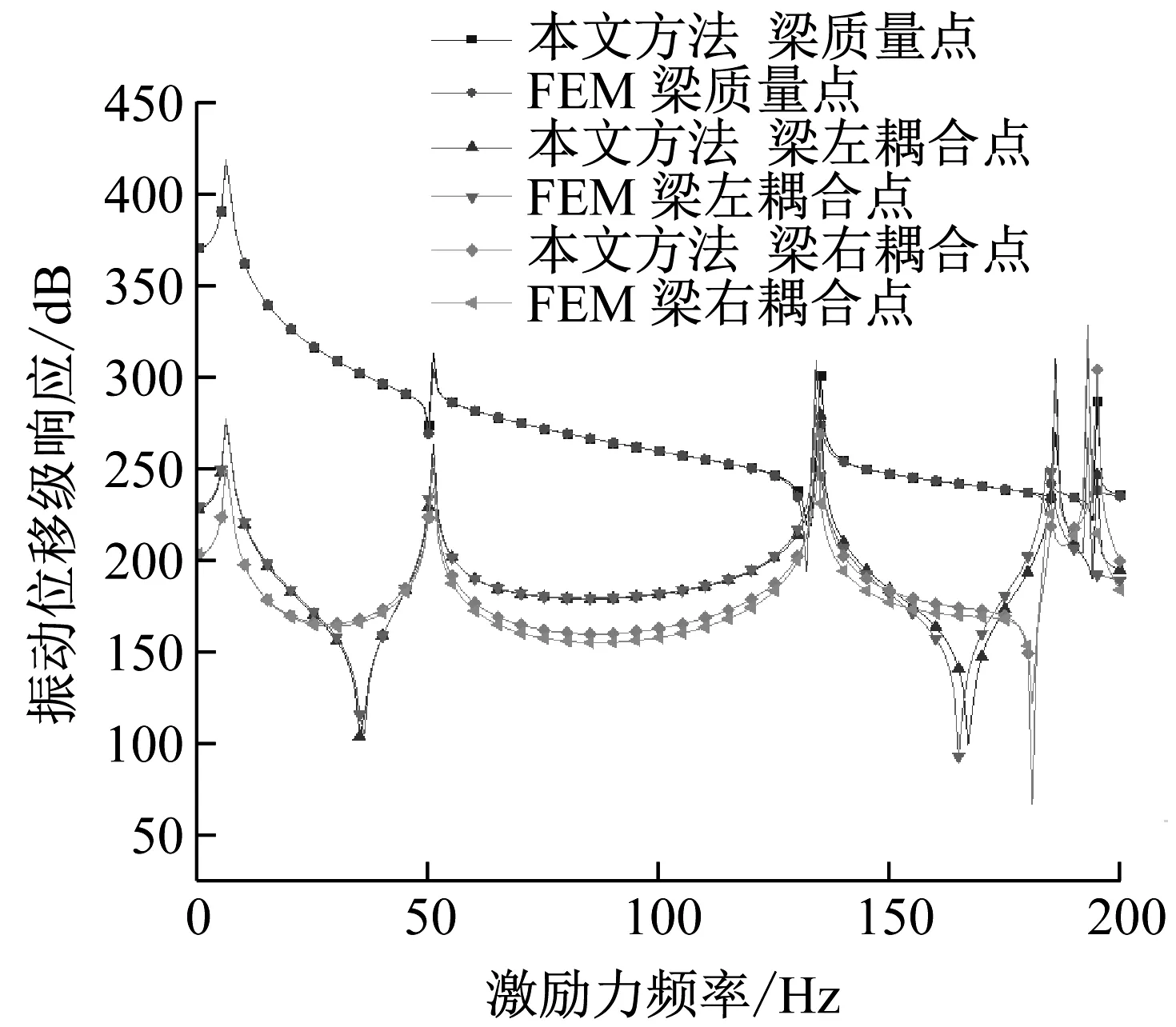
(a) 梁结构

3 参数对耦合系统振动特性影响

3.1 耦合弹簧组刚度对系统振动特性影响

由前文理论推导部分可知，耦合弹簧组储存的弹性势能是构成整个系统的重要部分。显然，耦合弹簧刚度值将直接影响其储存的弹性势能大小，进一步影响耦合系统的振动特性。

在前文的计算中，耦合弹簧组选取了较大的耦合刚度值1×108。参照边界弹簧收敛性讨论部分的内容，这种情况下梁结构和圆柱壳结构耦合点之间应该为一种“强耦合”的状态，即梁节点与圆柱壳节点的对应位移严格相等。当耦合弹簧的刚度减弱时，耦合点之间可能会转化为一种“弱耦合”的状态。当这种状态发生的时候，耦合系统振动特性应该会产生明显的变化。下面将保持系统其余参数不变且圆柱壳取简支-简支边界条件，通过改变耦合弹簧组的线弹簧刚度取值，验证这一猜想。令kL,x=0，其余各耦合线弹簧刚度采用相同取值。

从图8中可以看出，与边界弹簧随刚度值增加的变化规律类似，耦合弹簧刚度值增大到一定量之后，系统固有振动特性将会趋于稳定。此时，耦合刚度的改变对系统振动性能影响可以忽略不计，具体表现为刚度取值为1×108和1×1010的响应曲线有着高度重合性。而前文中关于“强弱”耦合状态转变时耦合系统将产生振动特性变化的猜想也在图中得到了明显体现。系统振动特性的变化可以分为两个方面。首先，从图8和图9(a)、9(b)可以看出，在“弱耦合”阶段，梁结构与壳结构在对应耦合点的位移级响应曲线虽然变化趋势基本吻合但存在明显“落差”，说明由梁结构质量点处激励力产生的振动在耦合点处产生了明显衰减；随着耦合刚度增加，达到“强耦合”阶段后，对应耦合点处两者位移级响应曲线基本重合了，表明此状态下两者振动传递几乎没有损失。其次，在耦合刚度较小的“弱耦合”阶段，随着耦合弹簧刚度增加，系统的势能增大，固有频率整体有增大的趋势，在图8中表现为受迫振动位移响应共振峰整体右移，直至达到“强耦合”阶段后，共振峰不再产生明显移动。

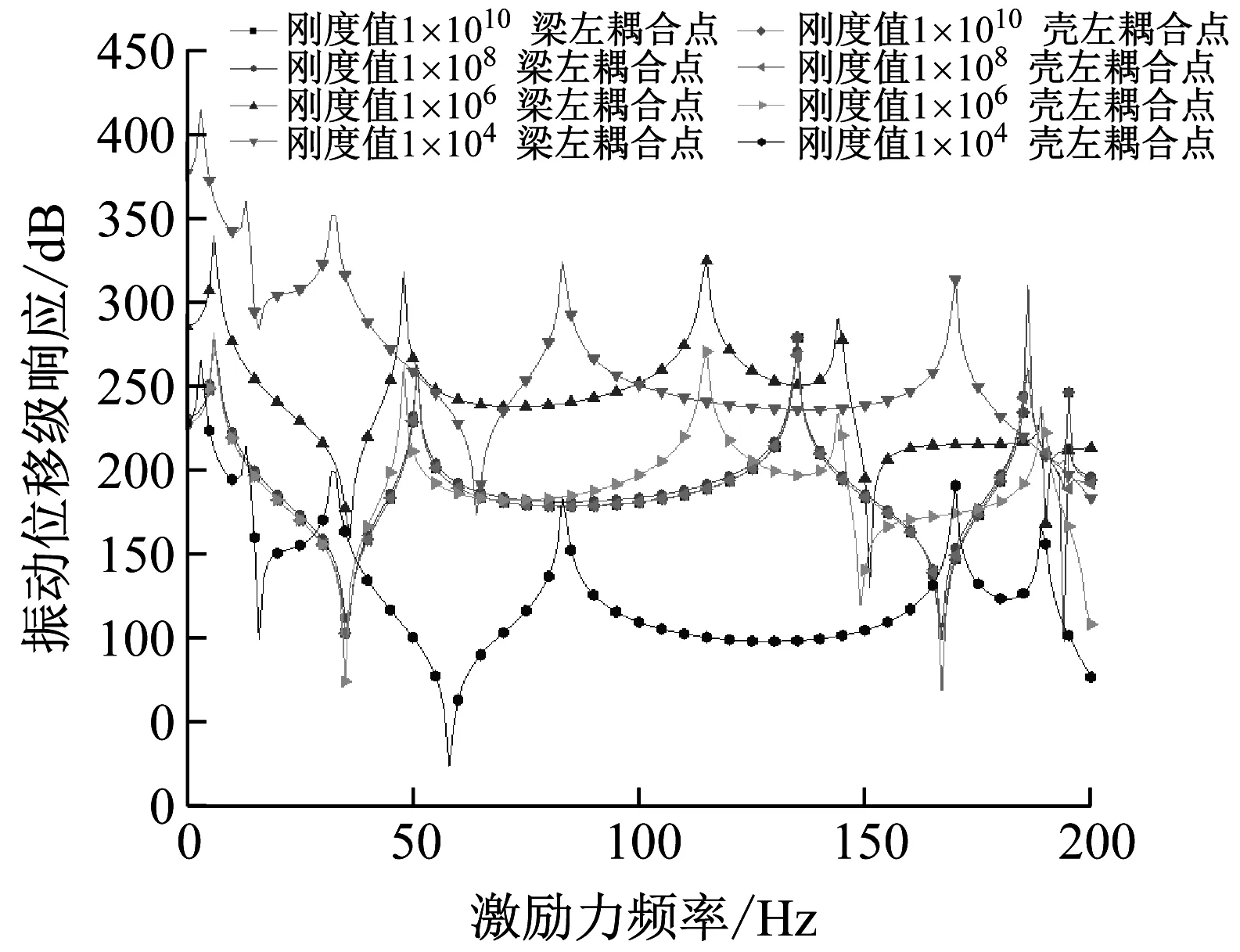
图8 耦合弹簧刚度取值变化时梁及壳结构左耦合点处

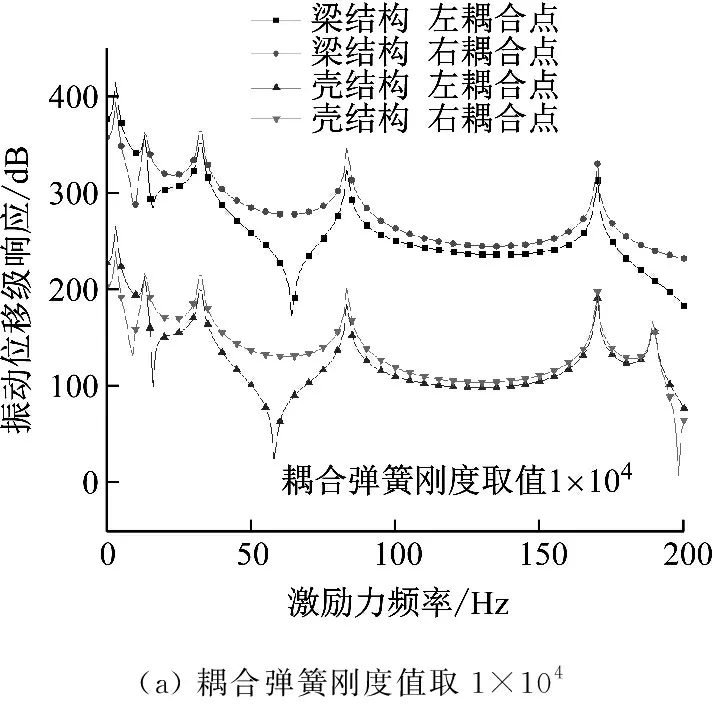
图9 不同耦合弹簧刚度值下梁及壳结构耦合点处位移级响应对比

3.2 旋转耦合弹簧对系统振动特性影响

以上工作仅考虑梁-壳结构之间的线位移耦合，但实际上两者之间还存在耦合弯矩作用，即还应考虑本文耦合弹簧组中旋转弹簧的影响。仍然取圆柱壳为简支-简支条件下的计算模型，而各耦合弹簧如存在则刚度值取1×108。表5为各耦合弹簧对系统固有振动特性影响。

如表5所示，如考虑梁-壳结构之间的耦合弯矩作用，即添加旋转耦合弹簧后，由于耦合弹性势能的增加，系统的固有频率将会增大。此外，由于本文模型在垂(z)向及横(y)向上无耦合，因此耦合旋转弹簧也仅会对对应方向上的振动产生影响。

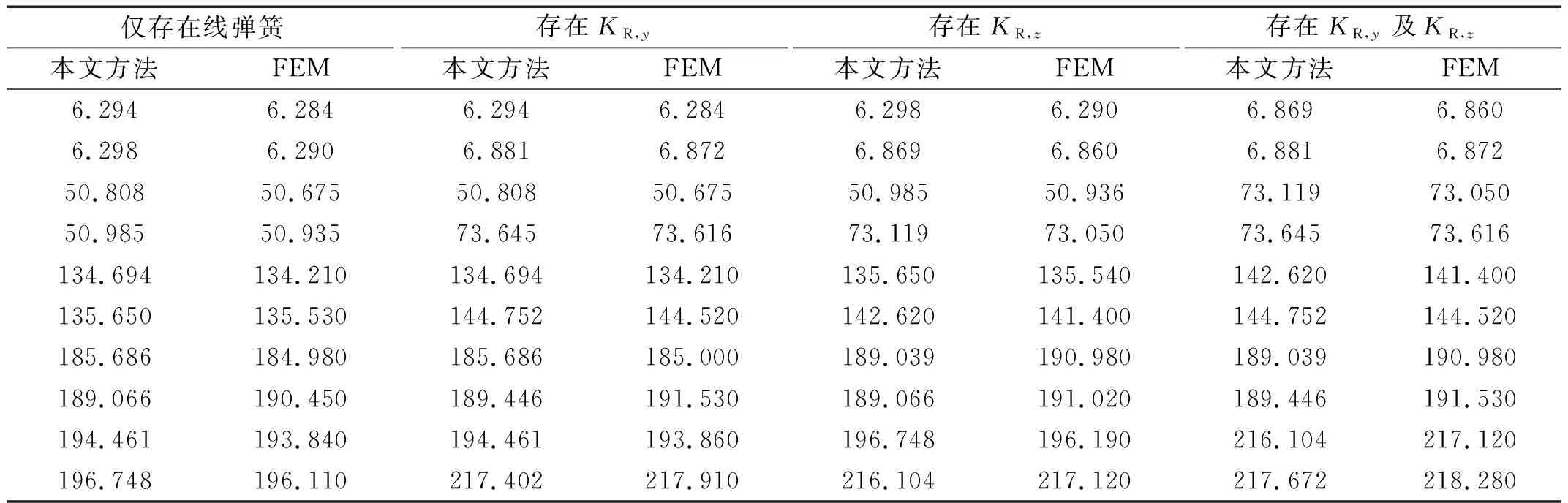
表5 不同耦合弹簧组合下系统前10阶固有频率

3.3 集中质量点质量对系统振动特性影响

由本文计算模型推导部分可知，附加集中质量的大小将直接影响梁结构的附加动能项，进而引起系统振动性能变化。下面分别取耦合弹簧刚度值为1×104和1×108且圆柱壳为简支-简支条件下的计算模型，研究仅改变附加质量大小时耦合系统振动性能变化。

从图10(a)及10(b)中可以看出，在本文探讨的变化范围内，集中质量点质量的增加对梁结构的振动位移响应有一定的抑制作用，响应曲线有下移的趋势；此外，当集中点质量增大时，附加动能项能量增加，系统固有频率减小，在图中反映为共振峰的左移。实际上，本文质量点为螺旋桨的简化，其质量大小的改变可视为由螺旋桨与水耦合作用产生的附连水质量效应，而本文计算结果也与附连水导致含桨系统固有频率降低的实际情况相符。

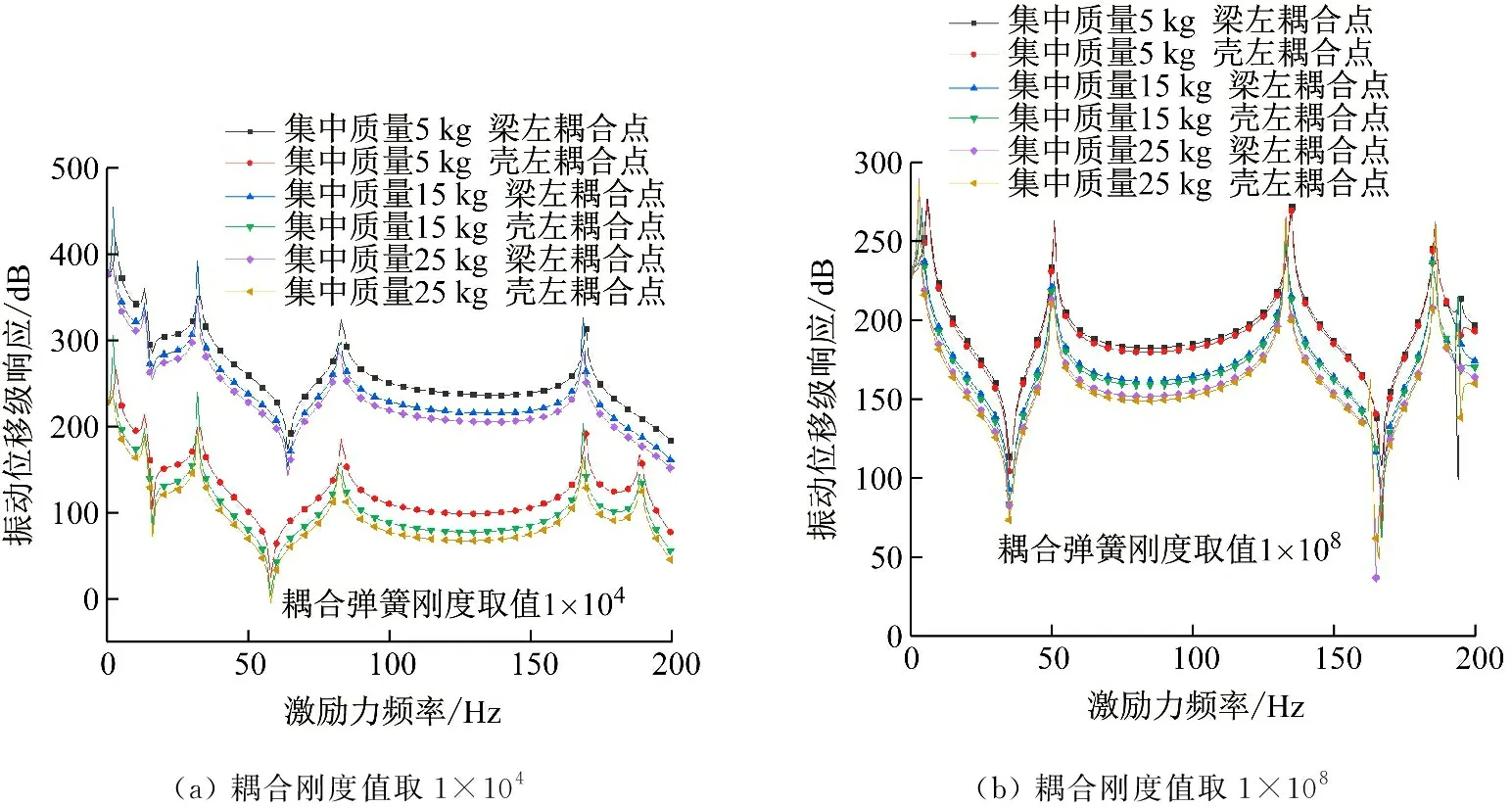
图10 不同耦合刚度值下集中质量点质量变化对结构左耦合点处位移响应影响

4 结 论

本文基于Rayleigh-Ritz法，引入改进傅里叶级数作为结构位移函数，结合边界弹簧组和耦合弹簧组，建立了梁-圆柱壳耦合动力学计算模型。通过改变边界弹簧组刚度值即可模拟各种经典圆柱壳边界条件，构建了适用范围广的动力学分析模型。与有限元法(FEM)软件计算结果的对比，验证了本文方法在计算固有特性及受迫振动响应时的正确性。随后，进一步分析了耦合刚度值和集中点质量等参数对梁-圆柱壳耦合系统振动特性的影响，得出了以下结论：

(1) 针对本文研究的梁-圆柱壳耦合系统，耦合系统的前4阶模态可视为支撑于刚体上的梁结构弯曲振动，梁结构与圆柱壳结构可视为解耦状态。此时，壳体边界约束条件变化对系统固有频率几乎没有影响。

(2) 耦合弹簧刚度值处于较小的范围时，由于对耦合节点处对应方向的连续性约束较弱，梁壳耦合结构将在耦合节点处出现位移不连续的现象。此时，两者的振动位移响应曲线虽然趋势相同，但响应幅值出现落差，表明振动在结构中的传递产生了衰减。

(3) 此外，由于集中质量点附加质量对结构振动动能项的影响，梁端点处的集中质量点质量对耦合系统振动特性有一定的影响，系统会出现一定的固有频率改变(响应曲线共振峰偏移)，对应测点处的振动位移响应结果也会产生一定的变化。