面向薄壁零件的黏滞阻尼器设计及试验

陈甜甜， 李道靖， 张素燕， 刘 争， 杨毅青

(1.北京航空航天大学 机械工程及自动化学院，北京 100191； 2.首都航天机械有限公司，北京 100076)

薄壁零件被广泛应用于航空航天领域，对其加工精度和表面质量要求极高。由于薄壁件刚性差，切削动力学特性随着加工过程快速变化，导致薄壁件切削稳定性多变，极易发生颤振，难以达到加工要求，极大的影响刀具寿命和加工效率[1]。为了抑制薄壁件在加工中的振动，主要采用工艺优化、主动抑振技术和被动抑振技术等。被动抑振技术具有实施方便、效果明显等优点，在切削加工过程中被普遍采用，其主要可分为动力吸振和耗能减振。

动力吸振方式形式多样，主要以调谐质量阻尼器为代表，其中单自由度吸振器因其结构简单、抑振效果明显的优点被广泛采用。为使动力吸振器在质量不变的情况下发挥最佳的抑振效果，要对其刚度、阻尼等参数进行优化，国内外学者在这个方向做了大量研究，提出了一系列的优化准则和优化算法。Den Hartog[2]以抑制主结构振幅为目标，利用“不动点”理论，推导出主结构无阻尼情况下单自由度阻尼器H∞准则的解析解，Crandall[3]以主系统幅频特性曲线与频率轴围成面积最小为目标提出了H2优化准则，Moradi[4]选取了多组铣削参数，以刀具振动最小化为目的对阻尼器位置与刚度优化进行研究。单自由度动力吸振器性能优越，抑振效果明显，然而其对频率匹配要求高，只能抑制某一特定模态振动。针对多模态振动抑制的多自由度动力吸振器结构设计和参数优化较为复杂，无法很好的适应薄壁零件切削时出现的多阶振动模态和动力学特性快速多变的特点[5-6]。

耗能减振通过增加结构阻尼，利用相对运动耗散振动能量，起到减小振动的作用。根据作用原理可将其分为黏弹性阻尼技术、电涡流阻尼技术、摩擦阻尼技术、冲击阻尼技术和黏滞性阻尼技术。Kolluru等[7]提出了在工件表层粘贴薄柔性层与质量块的阻尼减振方案。Shi等[8]设计了一种附着于薄壁零件上的黏弹性阻尼器并成功应用于铣削加工振动抑制。Yang等[9]设计了一种可调刚度电涡流阻尼器，旨在抑制薄壁零件铣削加工中工件的振动。Ziegert等[10]基于库仑摩擦理论提出了一种指状摩擦减振铣刀，并从理论和实验方面论证了该铣刀对高频振动的抑制效果。Yang等[11]基于冲击理论，结合悬臂梁模型设计了一种冲击阻尼器，并将其成功运用到车刀上。Gubanov[12]基于空气黏滞阻尼效应设计了一种耗能阻尼器，对加工振动抑振效果明显。耗能减振通过提高系统阻尼抑制系统振动，相较于动力吸振方式，其抑振效果受目标模态动力学参数变化的影响较小，因此适合具备多阶弱刚性模态的薄壁件切削振动抑制。

综合以上，针对薄壁零件切削过程中动力学特性多变的特点以及动力吸振器适应性不足等问题，本文拟研究基于黏滞阻尼原理的被动阻尼减振技术，设计一种被动阻尼器，通过理论建模得出阻尼系数与流体动力黏度以及结构参数之间的关系，以空气介质为例，通过模态测试和激振试验对其阻尼特性进行测试。

1 理论建模

1.1 运动方程推导

基于耗能减振原理的被动阻尼器其模型如图1所示，通过增加主结构的阻尼起到抑振效果，其中，k1、c1、m1分别为主系统的刚度、阻尼和质量，m2和c2分别为阻尼器质量和阻尼。

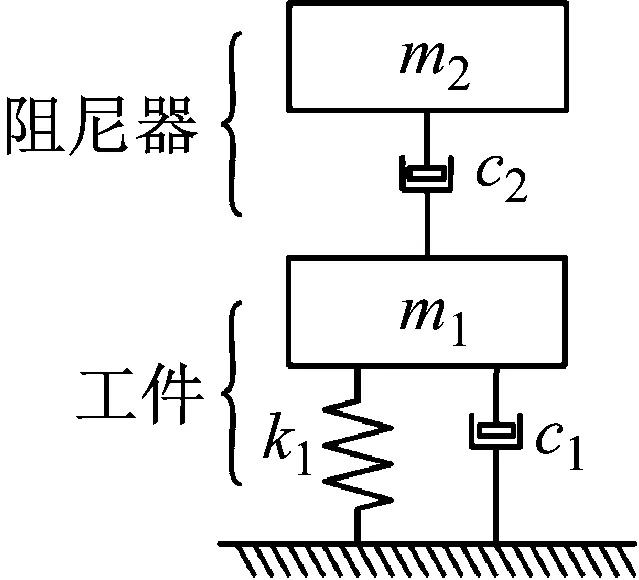
图1 耗能阻尼器动力学模型

其动力学方程如下

H(ω)=

(1)

假设主系统阻尼c1为零，对式(1)进行无量纲化，可得：

(2)

式中相应参数可表示为

式中：μ为阻尼器与主系统的质量比；ω0为主系统固有角频率；Ω为无量纲化的角频率。

则无量纲频响函数实部G(Ω)为

(3)

根据铣削颤振理论[13]，临界稳态切深为

(4)

式中：aplim为临界稳态切深；Kt为切向力系数；Z为铣刀齿数；β0为方向系数平均值；Gmin为频响函数实部最小值。由式(4)可知，在加工条件一定时，频响函数实部最小值与稳态切深呈负相关。

根据Sims的不动点理论[14]，式(3)存在三个不动点

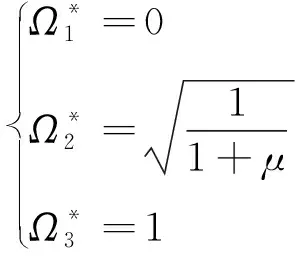
(5)

(6)

所以，阻尼器的最佳阻尼系数c2opt取值为

(7)

取μ=1，在不同c2对G(Ω)进行仿真，结果如图2所示。

图2 G(Ω)仿真

由图2可知，在阻尼器阻尼系数c2小于其最优阻尼系数c2opt时，随着阻尼器阻尼c2的增大，频响函数最小负实部增大，系统稳定性提高；当c2达到最优阻尼系数c2opt时，频响函数最小负实部达到最大值；当c2超过最优阻尼系数c2opt时，频响函数最小负实部随着c2增大而减小，系统稳定性降低。因此，对于一个给定的系统来说，当阻尼器阻尼系数c2为最佳阻尼系数c2opt时，系统稳定性最好。

1.2 黏滞阻尼原理

在流体流过圆环缝隙时，如图3所示，由于流体具有黏度，所以其会提供一个黏性力Ff，当圆环缝隙的外壳与内部发生相对运动时，这个黏性力Ff会阻碍这个相对运动，即对运动提供了一定的阻尼。基于此原理，设计一种被动阻尼器如图4所示。

图3 环状缝隙

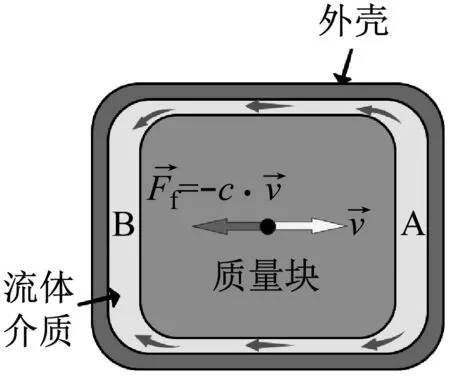
图4 阻尼器结构

阻尼器由圆柱体外壳、质量块以及内部均匀填充的流体介质组成。在外壳与质量块间留有一定的径向间隙g，当阻尼器随工件一起振动时，内部质量块会沿轴向运动。当内部质量块相对外壳以如图4所示速度运动时时，会对A处介质产生挤压，迫使该处介质沿着径向间隙g流向B处，在这个过程中由于流体介质具有黏性，因此会提供一个作用力Ff，该力会阻碍质量块的轴向运动且会将质量块动能的一部分转化为热能耗散，从而耗散振动能量，起到抑振的效果。

由流体的缝隙流动相关理论可知[15]，流体在圆环形缝隙中流动时，其流量Q可由下式推出

(8)

式中：h为缝隙宽度；a为环状缝隙截面周长；μa为流体动力黏度；L为环状缝隙轴向长度；ΔP为缝隙前后两侧压强差。

对于环状缝隙来说，由于其缝隙宽度h较小，因此其可以等效看作平板缝隙流动，即其截面周长为

a=πD

(9)

式中，D为质量块直径。缝隙长度L与质量块长度l相等，即:

L=l

(10)

缝隙宽度为径向间隙g的一半，即：

(11)

假设质量块与外壳之间的相对运动速度为v，则流体在缝隙中的流动速度也为v，则流过缝隙的流体流量Q为

(12)

质量块两侧压强差给予质量块的阻力Ff为

Ff=ΔPSd

(13)

因此，可以求出阻尼器的阻尼系数为

(14)

由式(14)可知阻尼器的阻尼系数与流体介质的动力黏度μa和质量块与外壳之间的径向间隙g有关。其与流体动力黏度大小成正比，与径向间隙的三次方成反比，因此从理论上流体的动力黏度越大，质量块与外壳之间的径向间隙越小，阻尼器所具有的阻尼系数越大。

结合式(7)与式(14)，可知在选定流体介质后，即可计算出阻尼器径向间隙g

(15)

2 结构设计

传统阻尼器装夹通常使用粘贴或螺栓紧固的方式，其会对工件表面造成一定影响，因此选择真空吸附的方式对阻尼器进行安装和固定。选择的真空吸盘型号为SMC公司型号的ZP2-TB20MTN-H5，转接头通过两个正交孔形成通气回路，使吸盘与工件表面间的空气可由该回路被真空泵抽出，从而形成负压，使装置能够牢固的固定在工件表面。为尽量减少零件个数，使整个装置更加简洁可靠，使用转接头的端面代替阻尼器端盖。真空转接头如图5所示。

(a) 三维模型

依据1.2节黏滞阻尼原理，设计的阻尼器结构如图6所示，其由外壳与内部质量块组成，内部质量块质量与工件模态质量相同，质量块与外壳的径向间隙由式(15)计算得出，内部流体介质选择空气。

(a) 三维模型图

3 模态测试

设计圆筒铝合金薄壁框(直径300 mm，高80 mm，壁厚8 mm)作为抑振对象，通过模态试验和激振试验测试本文所述阻尼器效果。

采用模态试验测试本文所述阻尼器的阻尼特性。试验设备如表1所示。

表1 模态测试试验设备

测试对象采用三角定位安装方式，分别于Ⅰ、Ⅱ、Ⅲ三个位置进行压紧固定，其上被等间距划分为1～6六个位置，分别对这六个位置的频响函数进行测试。模态测试安装如图7所示。

(a) 工件安装及测试区域

对工件进行交叉点频响函数模态测试，测试时力锤敲击点与阻尼器安装点保持在位置1不变，加速度计分别安装在1～6各区域并测试该点频响函数。测试结果如图8所示。

(a) 各位置频响函数幅值

由图8(a)可以看出，在安装阻尼器后，1～6各位置振动模态峰值均有明显下降，最高可使振动模态峰值下降约60%。由图8(b)可知，在安装阻尼器后，各位置频响函数最小实部均有明显提高，说明在安装阻尼器后，系统稳定性具有明显提升。

对模态测试得到的频响函数进行参数辨识，在未安装阻尼器时零件阻尼比为0.403%，通过仿真，所设计的阻尼器理论上应能使零件阻尼比达到0.943%，实际测试中安装阻尼器后的零件阻尼比平均达到了0.876%，由此可以看出，阻尼器实际达到的阻尼参数与设计参数较为接近。

通过模态测试得到零件安装阻尼器前后的频响函数，并将其导入Cutpro软件中进行铣削颤振稳定域图仿真。材料为铝合金7075，其切向切削力系数Ktc为897.48 N/mm2，径向力系数Krc为205.95 N/mm2，在4齿圆柱铣刀槽铣条件下绘制铣削加工稳定域图，如图9所示。从图中可以看出，在安装阻尼器后，最小临界切深提高了约2.08倍，说明本文所提出的被动抑制振动技术能在铣削过程中发挥较好的效果。

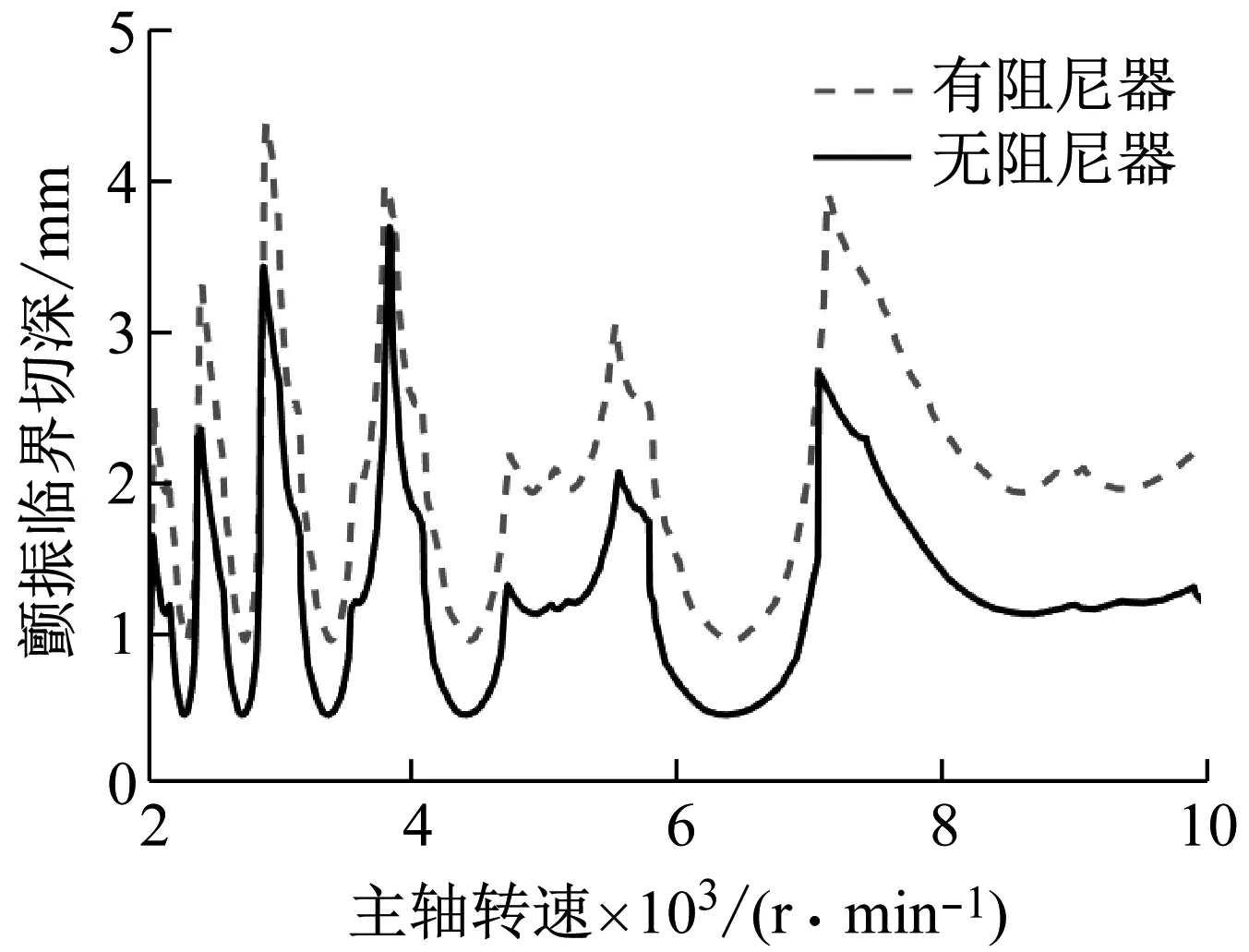
图9 颤振稳定域预测图

4 激振试验

对所述工件进行激振试验，检测所设计阻尼器在外界连续激励振动条件下抑振效果。激振器选择HEV-20电磁激振器。

在工件安装后，首先使用扫频确定工件安装后的共振峰频率，然后在共振频率处对工件进行激振，测试阻尼器的抑振效果。激振试验各装置安装情况如图10所示。

图10 激振试验

由模态测试结果可知，所述工件在图10所示安装环境下共振峰在1 000 Hz附近，通过激振器对频率范围50～2 000 Hz扫频得出工件的振动幅值如图11所示。

图11 50～2 000 Hz正弦扫频时的工件响应

由图11可知，在图10所示安装情况下，工件共有三个较为强烈的共振峰，分别为785 Hz、970 Hz和1 175 Hz。将阻尼器与加速度计固定在点1处，用激振器分别在这三个频率下对1～6点进行激振，测得安装阻尼器前后工件加速度对比如图12所示。

(a) 785 Hz正弦激励

由图12可以看出，在安装阻尼器后对工件振动具有明显的削弱作用，对扫频试验中振动较为明显的三个频率785 Hz、970 Hz和1 175 Hz，安装阻尼器后工件加速度分别平均降低了58%、60%和63%，且安装阻尼器后工件振动更为稳定，因此可知所述阻尼器能够有效的抑制工件振动。

5 结 论

薄壁件自身刚性差，切削加工过程中易发生振动。本文设计了基于黏滞阻尼原理的被动阻尼器，其通过真空吸附的方式吸附在圆筒薄壁零件上。在切削过程中，阻尼器将零件的动能转移到质量块上，并通过空气的黏滞阻尼进行耗散，从而起到抑制薄壁件振动的作用，抑制效果明显，针对薄壁件复杂加工过程具有较强的适应性。结论如下：

(1) 针对圆筒薄壁件的模态测试结果表明，所设计的基于流体黏滞阻尼原理的被动阻尼器具有良好的抑振效果，振动模态幅值最大可降低约60%。

(2) 将该阻尼器应用于圆筒薄壁件激振试验时，可明显降低工件振动幅值，激振试验表明薄壁圆筒零件振动加速度下降36%～67%，具有明显抑振效果。

(3) 安装阻尼器后，系统阻尼比从0.403%平均提升至0.876%，提升了约2.17倍，最小临界切深提升了约2.08倍。