预应力式压电能量采集器的模型和试验分析

王 海， 徐 罡， 杨春来， 金 标， 郑衍畅， 史 宁

(安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000)

随着可植入式电子和无线传感器技术的快速发展，利用环境能量为存在于网络节点的低功耗设备供电是一种新的供能方式。作为传统电源的替代品，从环境中采集振动能量是为无线传感器、可植入式电子设备和其他低功耗设备提供电能的有效方式之一。因为振动能量的采集受气候、温度等环境因素影响较小，所以在某些特定的传感节点上，收集振动能量更为可行。基于静电[1-2]、摩擦[3]、压电[4-9]和电磁[10-11]转换机制的振动能量采集器在过去十几年中被广泛讨论。目前为止，高输出功率仍然是振动能量采集器应用过程中的关键因素。

为了提高压电能量采集器的能量采集效率，研究人员设计出一些基于非线性方法[12-13]的压电能量采集器和二自由度的压电悬臂梁能量采集方法。例如：引入磁场力、利用碰撞原理、采用翘曲梁等方法。例如，Yang等[14]提出了一种基于内共振的非线性能量采集器，这种能量采集器的主体是一个压电悬臂梁，悬臂梁上有一个可移动的磁体，磁体连接在弹簧上，距悬臂梁不远处有一个固定磁体，活动磁体可以沿着梁滑动。设计这样的结构目的是为了减小梁的刚度，增强悬臂梁的运动失稳，从而提高能量采集器的输出功率。试验结果表明，振幅和电压的频率响应均显示出双重弯曲效应，表现出更宽的工作带宽。与只有两个固定磁体的双稳态能量采集器相比，这种能量采集器的带宽要大两倍。Hu等[15]设计了一种带有阻挡块的两自由度压电能量采集器，与现有文献研究的基于碰撞的能量采集器不同的是没有在底座上安装止动块，而是将止动块安装在主梁上。根据得到的试验结果，在相同的条件下，与线性单自由度和两自由度能量采集器相比，其工作带宽分别拓宽了232.1%和289.8%。并且与线性单自由度和两自由度能量采集器相比，能量采集器最大输出功率幅值分别提高了64.4%和118.9%。除此之外，Yildirim等[16]提出了一种基于参数激励方法的非线性能量采集器。除了利用非线性力和非线性振动结构外，改变压电悬臂梁的初始条件也是提高能量采集效率的一种有效途径。初始应力会引起结构弹性刚度的变化，可以用来调整结构的共振频率和模态振型。本文设计了一种基于预应力梁的压电式能量采集器。为了验证能量采集器的采集性能，建立该装置的数学模型并进行数值仿真，设计并搭建了试验平台，对在有无预加轴向拉力作用下的能量采集性能进行了测试和分析。

1 基于预应力梁的压电式能量采集器

1.1 能量采集器结构

图1为压电能量采集器的结构图。由于这里的预应力梁为细长梁，基于经典的欧拉伯努利梁理论[17]，忽略梁的剪切变形，悬臂梁在预加载荷和外部荷载作用下，其梁的微分单元发生纵向位移、横向位移和弯曲变形。单元的形变量可以通过其纵向位移u(x,t)和横向位移(x,t)分析，在该试验装置中悬臂梁刚度很大且轴向拉力较小，轴向位移相对于横向位移为高阶小量，根据材料力学中应力应变关系，预应力存在虽然产生了轴向变形，但轴向变形进一步影响横向位移，所以预应力的存在影响横向位移，为了简化计算，得到压电能量采集器的近似解，因此只考虑横向位移。

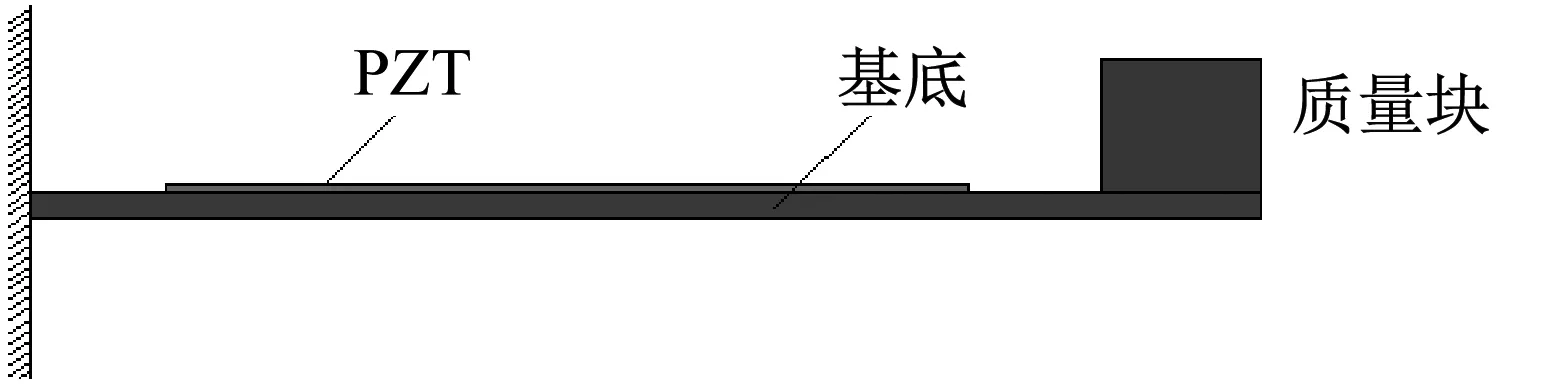
(a) 传统的压电能量采集器

1.2 能量采集器数学建模

建立欧拉-伯努利压电悬臂梁的非线性动力学方程，忽略剪切变形，沿x,z方向的位移

u3=0+cosΩt

(1)

式中：u1,u3分别为梁的x,z方向的绝对位移；u0,0分别为梁的中性面内的x,z方向相对位移；,Ω分别为激励幅值和激励角频率。

本文要研究压电悬臂梁结构的非线性振动，所以在位移应变关系中，我们考虑了几何非线性，求得的位移应变关系为

(2)

对于压电材料，压电本构方程如下

(3)

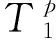
(4)

式中，ρs,ρp为金属层和压电层的材料密度。

忽略悬臂梁自由端的转动惯量，自由端质量块的动能

(5)

金属层和压电层的势能

(6)

电压项只与时间有关应乘H(x)-H(x-L)，H(x)为亥赛维函数。

阻尼力和电荷所做的功

(7)

(8)

可以得到下式

(9)

(10)

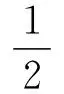
(11)

其中：

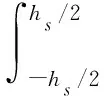
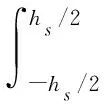
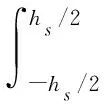
(12)

式中：b为宽度；hs为基底梁的厚度；hp为压电片的厚度。

其中:

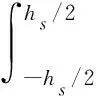
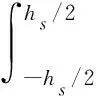
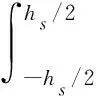
(13)

(14)

(15)

由于压电片很薄，对梁的中性层影响较小，把梁的几何中心近似看成中性层，因此将YJ,I11,ϑ1近似等于零。

忽略式(9)中的惯性量得

u″+′″=0

(16)

式(16)对x进行积分得

(17)

由于预应力的作用，轴向位移的边界条件为：u(0,t)=0,u(L,t)=-pL/(YA)，把边界条件代入式(17)求得

(18)

c2(t)=0

(19)

把c1,c2代入u(x)得

(20)

(21)

上面u和u′的导数代入控制微分方程

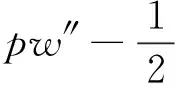
(22)

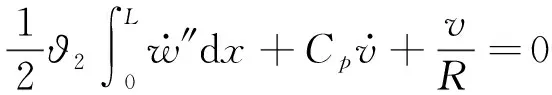
(23)

方程组表示了预应力压电悬臂梁的机电耦合性质。

1.2.1 无量纲化

对上述偏微分方程的边值问题，采用分离变量法

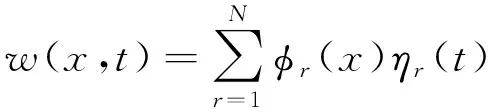
(24)

式中：φr(x)为第r阶模态振型函数；ηr(t)为第r阶模态响应函数。

假设压电悬臂梁受到简谐激励，方程中的受迫项可以写成

(25)

式中，0，ω分别为基础激励振幅和激励频率。把式(25)代入系统的控制微分方程得

(26)

(27)

其中

(28)

由于a1≈Ο(1)，我们可以忽略几何非线性对加速度的影响，引入以下无量纲变量。

(29)

用上述的尺度，无量纲方程可以写成

(30)

(31)

其中

(32)

1.2.2 摄动解的构造

采用多尺度法求解非线性方程组，得到一阶近似解。首先我们引入了一组新的时间尺度的自变量

Tn=εnt

(33)

式中:ε为时间尺度参数。Tn函数对时间求导

(34)

(35)

其中Dn=∂/∂Tn。因此，为求解η(t)、v(t)，假设

η(t)=η0(T0,T1)+εη1(T0,T1)+O(ε2)

(36)

v(t)=v0(T0,T1)+εv1(T0,T1)+O(ε2)

(37)

其中参数k1～k4定义为

k1=εk1,k2=εk2,k3=εk3,k4=εk4

(38)

考虑主共振ω～ω1，引入调谐量σ，令ω=ω1+εσ。 把上述定义的参数代入系统控制方程中，令ε0，ε1的系数等于零。

ε0：

D0v0+k6v0=k5D0η0

(39)

ε1:

k3v0+k4cos(ω1T0+σT1)

(40)

D0v1+k6v1=k5(D1η0+D0η1)-D1v0

(41)

上式的解可以表示为

η0=A(T1)eiω1T0+cc

v0=ZA(T1)eiω1T0+cc

(42)

式中：cc为复共轭项；A(T1)是关于T1的方程。其中:

(43)

把式(43)代入ε1方程组中，并令eiω1T0的系数等于零，得到:

(44)

把式(44)代入ε1方程组中得到

v1=0

(45)

为了得到式(44)的解，用极坐标的形式描述复值函数A(T1)

(46)

将A(T1)代入式(44)，然后把方程的实部和虚部分开得到

(47)

其中:

φ=σT1-θ

(48)

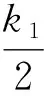
上面的偏微分方程组是不可解的，只能求出其稳态解，故令β′=φ′=0得到压电悬臂梁动力系统的稳态解，两个偏微分方程取平方，然后相加，得出

(49)

式中，β0为稳态振幅。为了表示动力系统的幅频特性曲线，式(49)可写为

(50)

从式(50)可知，对于某一幅值响应β0，其对应两个激励频率ω1，2，但这两个频率所对应的响应β0可能是不稳定的，为了表征解的稳定性，考虑如下的动力学系统的方程

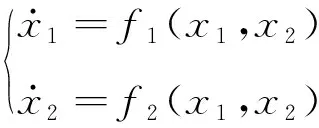
(51)

式中，x1,x2为状态量。则上述系统的雅可比矩阵为

(52)

根据上面求的幅值和频率的方程组，在本动力系统中状态向量β和φ，f1和f2的表达式如下

(53)

可得到系统的雅可比矩阵为

(54)

稳态运动的稳定性依赖于雅可比矩阵的特征值，上式所对应的特征方程如下

(55)

展开此行列式，得到

(56)

该运动系统的本征值如下

(57)

其中

(58)

根据以上公式可绘制出系统的稳定性，如图2所示。

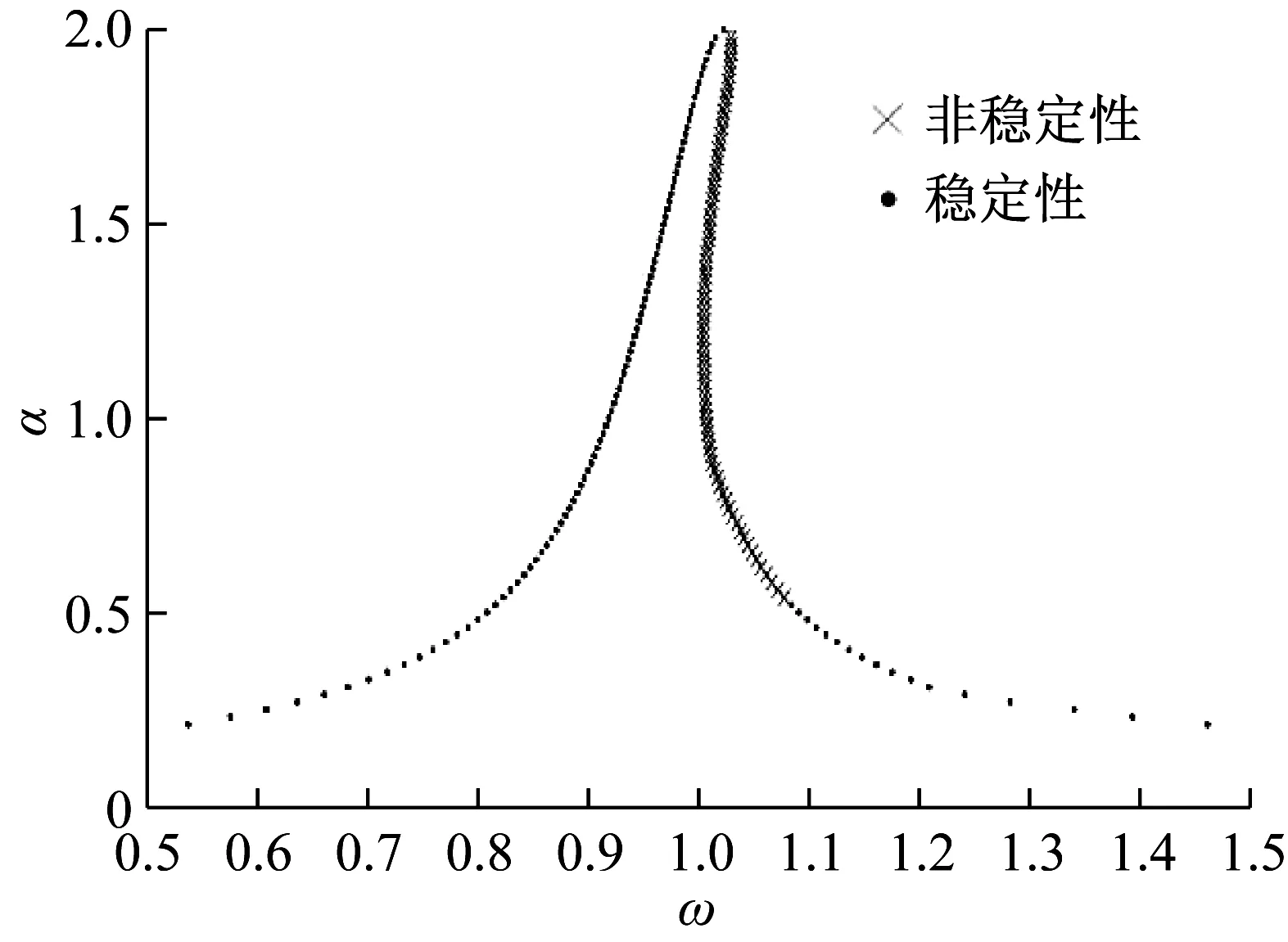
图2 幅频关系的稳定性

利用这些结果，得到位移和电压的表达式

(x,t)=rβ0φ(x)cos(ω1t+θ)-

(59)

(60)

平均输出功率

(61)

把v(t)代入式(61)得到

(62)

2 数值仿真和分析

通过MATLAB软件及1.2中的公式对压电能量采集器的力学行为进行数值模拟，进而评估该装置的能量采集性能。表1给出了能量采集装置悬臂梁和压电材料尺寸和性能参数。

表1 能量采集器的尺寸和材料参数

能量采集装置外接激励振动装置，为了使压电能量采集装置输出最大功率，振动装置的激励频率等于悬臂梁的固有频率，能量采集装置输出最大功率。该试验通过改变轴向弹簧的轴向拉力从而改变压电悬臂梁的固有频率和增大自由端的垂直方向的外载荷。

式(50)表达了PZT-5H表面的电压差，通过MATLAB绘制在不同轴向力作用下，频率和PZT-5H上下表面电压差的关系，如图3所示。

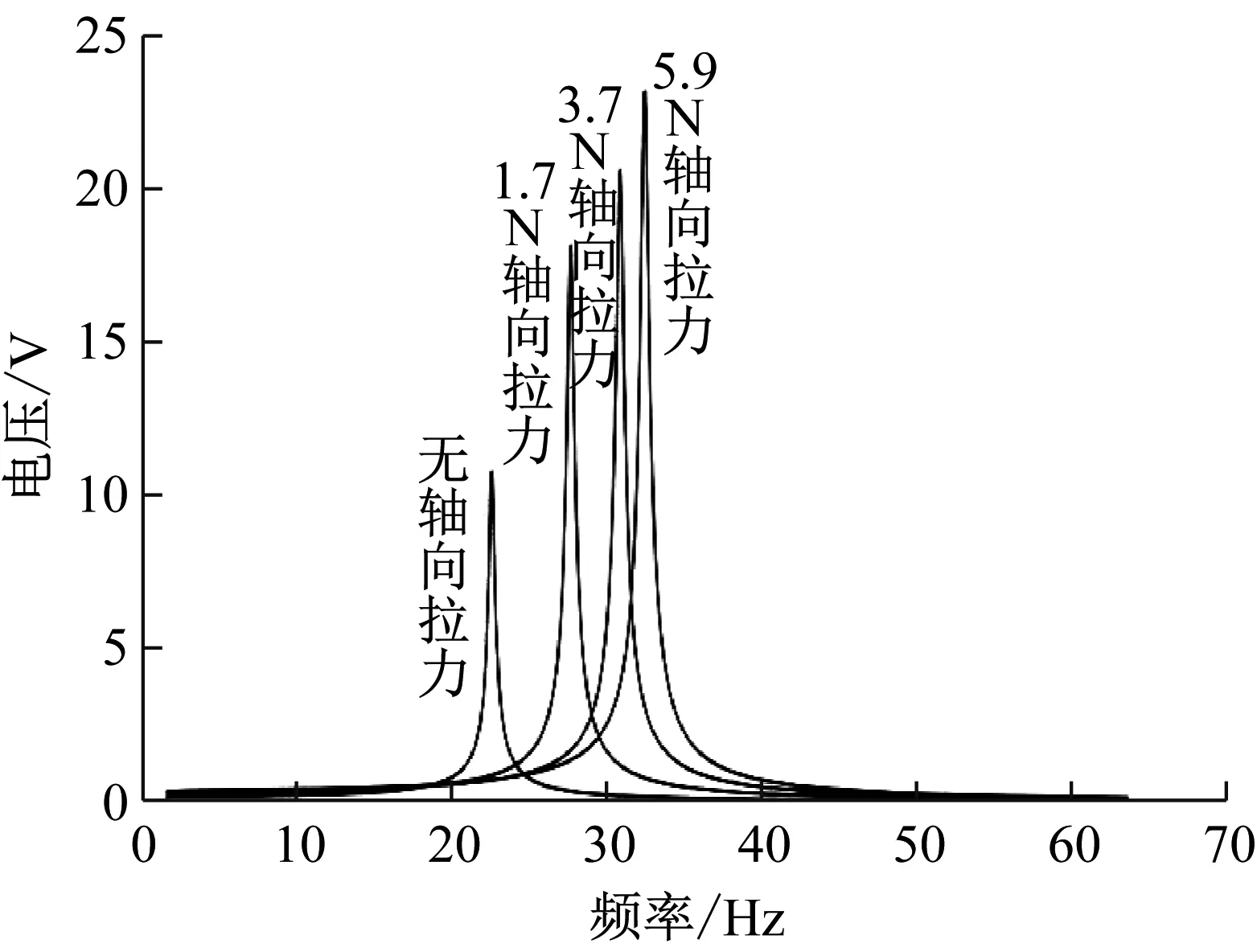
图3 不同激振频率下的开路电压

从图3可以看出增大轴向拉力，悬臂梁的固有频率相应增加。初始轴向拉力从0到5.9 N，固有频率从22.62 Hz增大到32.48 Hz。相应的PZT-5H上下表面的电压差从10.73 V增大到29.72 V。

式(62)近似描述了在外接不同负载电阻时的输出功率。图4表明了在外接电阻R从0到10 000 kΩ，悬臂梁自由端加不同轴向力，输出功率与电阻的关系。

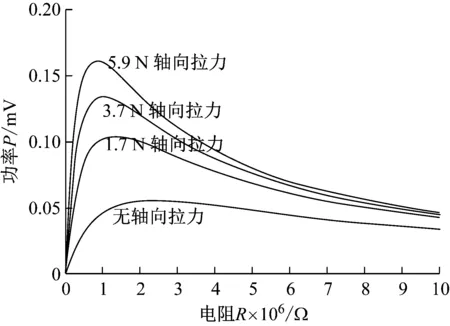
图4 在不同轴向拉力，输出功率与外接负载电阻的关系

从图4我们可以得到初始轴向拉力从0到5.9 N，输出功率从0.06 mW到0.16 mW。轴向拉力5.9 N时，外接824 kΩ输出功率达到最大值0.16 mW。

通过式(60)得到电压与时间的关系，在外接824 kΩ 的负载电阻生成如图5的不同轴向拉力作用下，开路电压的瞬态变化曲线。

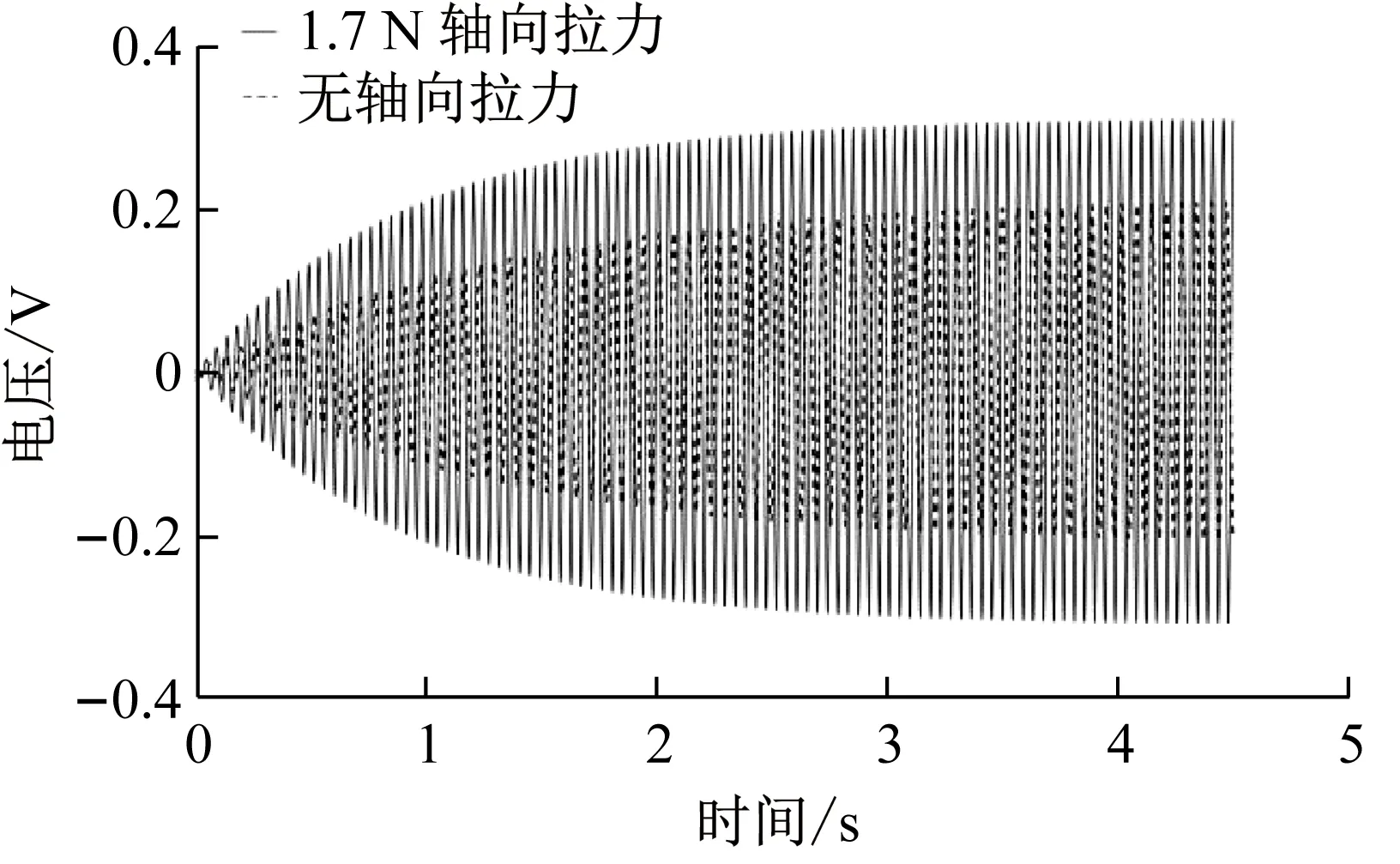
(a) 0和1.7 N轴向拉力

由图5(a)、(b)得在无轴向拉力作用下，能量采集装置的电压幅值大约为3.8 V，初始轴向拉力1.7 N作用下，电压幅值为5.6 V，初始轴向拉力3.7 N作用下，电压幅值为8.9 V，初始轴向拉力5.9 N作用下，电压幅值达到11.3 V。

3 试验平台与结果分析

3.1 试验平台搭建

为了测试和验证预应力梁对压电能量采集器的能量采集效率的影响，本文设计了相关试验对所设计的能量采集器进行验证。如图6所示，该能量采集器的主体是铜制基底梁，在其上表面粘贴PZT-5H。图7为整个试验平台的实拍图。

图6 能量采集器安装图

图7 试验平台实拍图

如上所述铜梁的右端粘有一个钢制质量块，质量块的右端连接有弹簧，用于调节梁的预加载荷。在初始载荷的作用下，基于预应力梁的压电能量采集器的固有频率会产生一定的偏移。

3.2 结果分析

本节在相同加速度激励下，对不同轴向拉力作用下的能量采集器做了试验分析。通过改变激励的频率，得到在不同轴向拉力作用下，压电能量采集器的开路电压随频率的变化曲线。如图8所示，无拉力作用下，压电能量采集器在27.2 Hz时产生了15.6 V的峰值电压，初始预加1.7 N轴向拉力的压电能量采集器在29.3 Hz时的产生的峰值电压为22.8 V，3.7 N初始轴向拉力作用下的压电能量采集器在31.1 Hz时产生了24 V的峰值电压。与传统的压电能量采集器相比，在5.9 N初始轴向拉力作用下，压电能量采集器的开路电压提高11.6 V，当激振频率为31.8 Hz时，其开路电压达27.2 V。图8与图3的仿真结果对比发现，能量采集器的固有频率、开路电压变化趋势及峰值大小较吻合，随着轴向拉力的增大，导致刚度增大，从而使固有频率增大，最终导致电压的增大。当初始轴向拉力增大到5.9 N时，能量采集器的固有频率偏移了4.6 Hz。

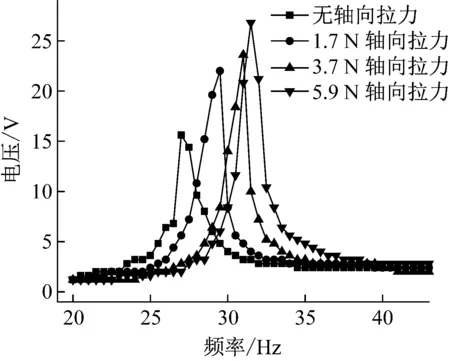
图8 不同激振频率下的开路电压

图9为在5.9 N轴向拉力作用下能量采集器的开路电压，分别为试验和仿真结果，由于试验误差的影响导致曲线未能重合，但在允许误差范围内，因此证明了试验及结论的正确性。

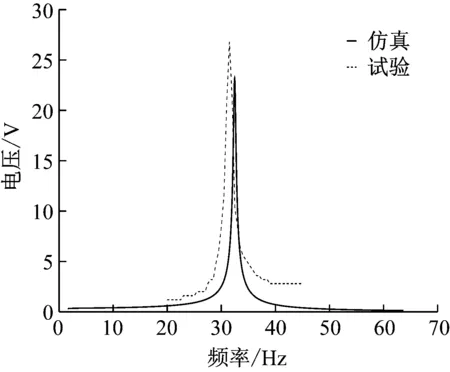
图9 5.9 N轴向拉力的试验与仿真结果对比

图10为压电能量采集器的一阶谐振频率和开路电压随轴向拉力增加的变化曲线。图11(a)、(b)为不同初始轴向拉力下，开路电压的瞬态变化曲线。无轴向拉力作用下，能量采集器的电压幅值2.1 V， 1.7 N初始轴向拉力作用下能量采集器的电压幅值为5.6 V，而3.7 N初始轴向作用下能量采集器的电压幅值为7.3 V，5.9 N初始轴向拉力作用下能量采集器的电压幅值为10 V左右。可以看出，预加轴向拉力可以提高能量采集器的输出电压。

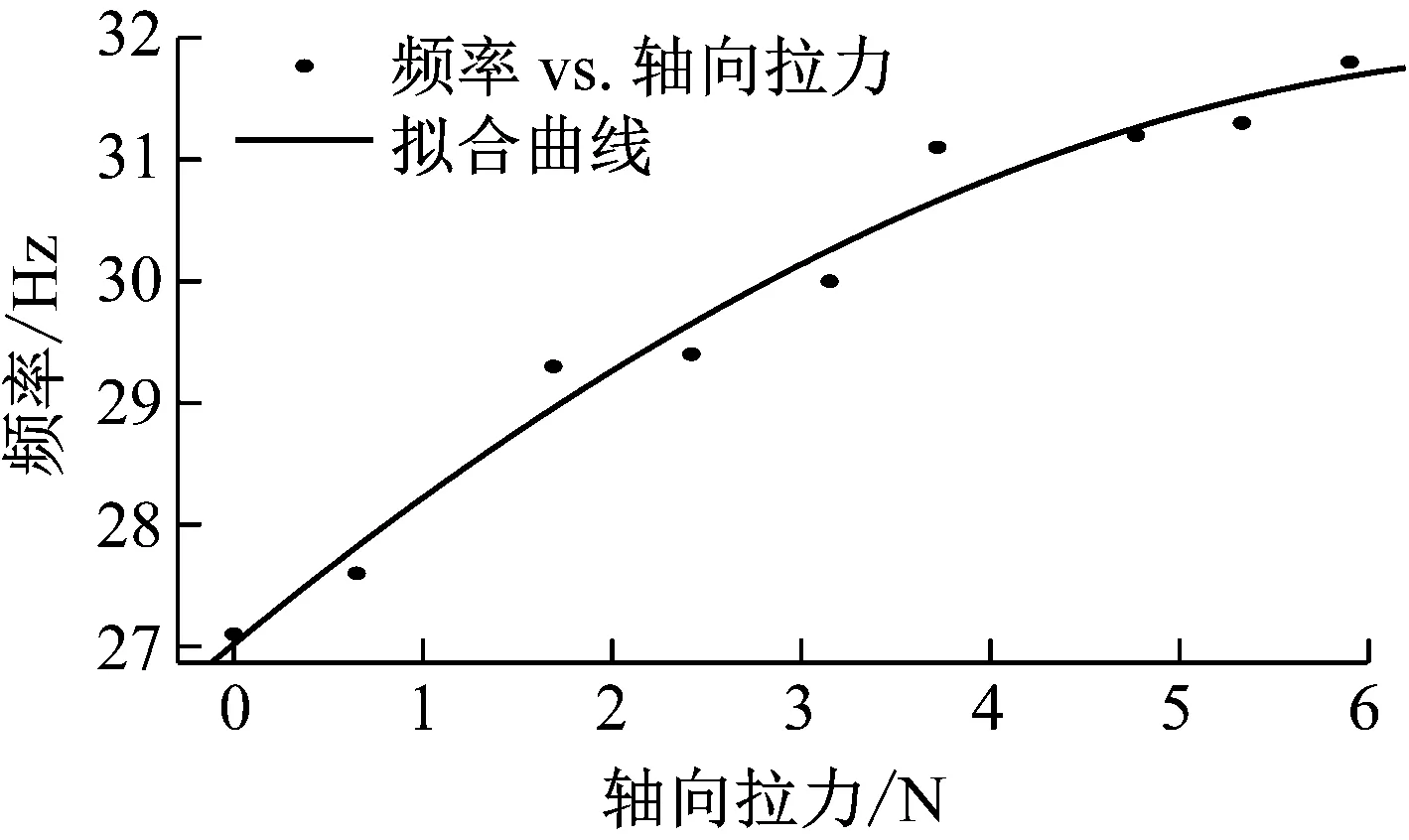
图10 一阶固有频率和开路电压与轴向拉力的关系

(a) 0和1.7 N轴向拉力

图12为在不同轴向拉力作用下压电能量采集器末端位移的FFT变换。该图表明，压电能量采集器末端振动的频谱特性与开路电压在扫频测试下的规律一致。随着轴向拉力的增大，压电能量采集器末端位移逐渐增大。能量采集器的固有频率也随着轴向拉力的增加偏移的更多，当初始轴向拉力增大到5.9 N时，能量采集器的固有频率偏移了4.6 Hz。图13为能量采集器在5.9 N初始轴向拉力作用下末端运动的相位图，该图表明在简谐激励作用下压电能量采集器末端做周期运动。

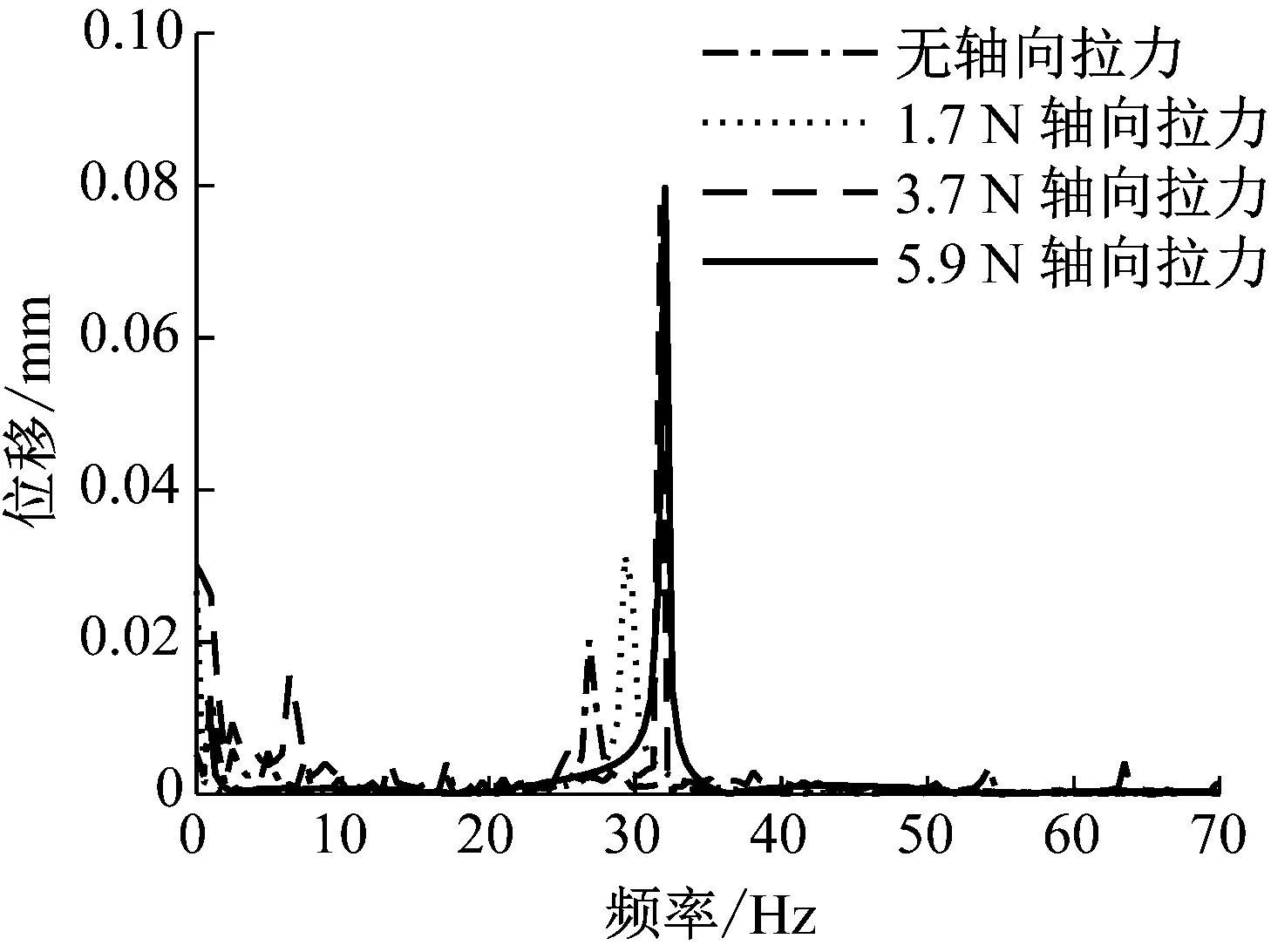
图12 末端位移的FFT变换曲线

图13 末端运动相位图

为了测试压电能量采集器在有或没有初始载荷条件下的充电性能,对100 μF电容器进行了15 s的充电测试。图14和表2分别给出了充电试验电路和充电测试结果。与无轴向拉力的压电能量采集器相比，5.9 N轴向拉力作用下的压电能量采集器充电电压提高了1.55 V。图15为不同轴向拉力作用下, 能量采集器对电容充电的平均功率曲线图，从图中可以看出,随着轴向拉力的增大，充电的功率呈增大的趋势。上述分析表明，预加轴向拉力从0到5.9 N，能量采集器的效率能提高83.1%。虽然轴向拉力使压电能量采集器的谐振频率发生了偏移，但其固有频率仍在低频范围内。因此，可以考虑采用这种预应力梁来提高压电能量采集器的能量采集效率。

图14 充电试验的试验电路图

表2 电容充电数据

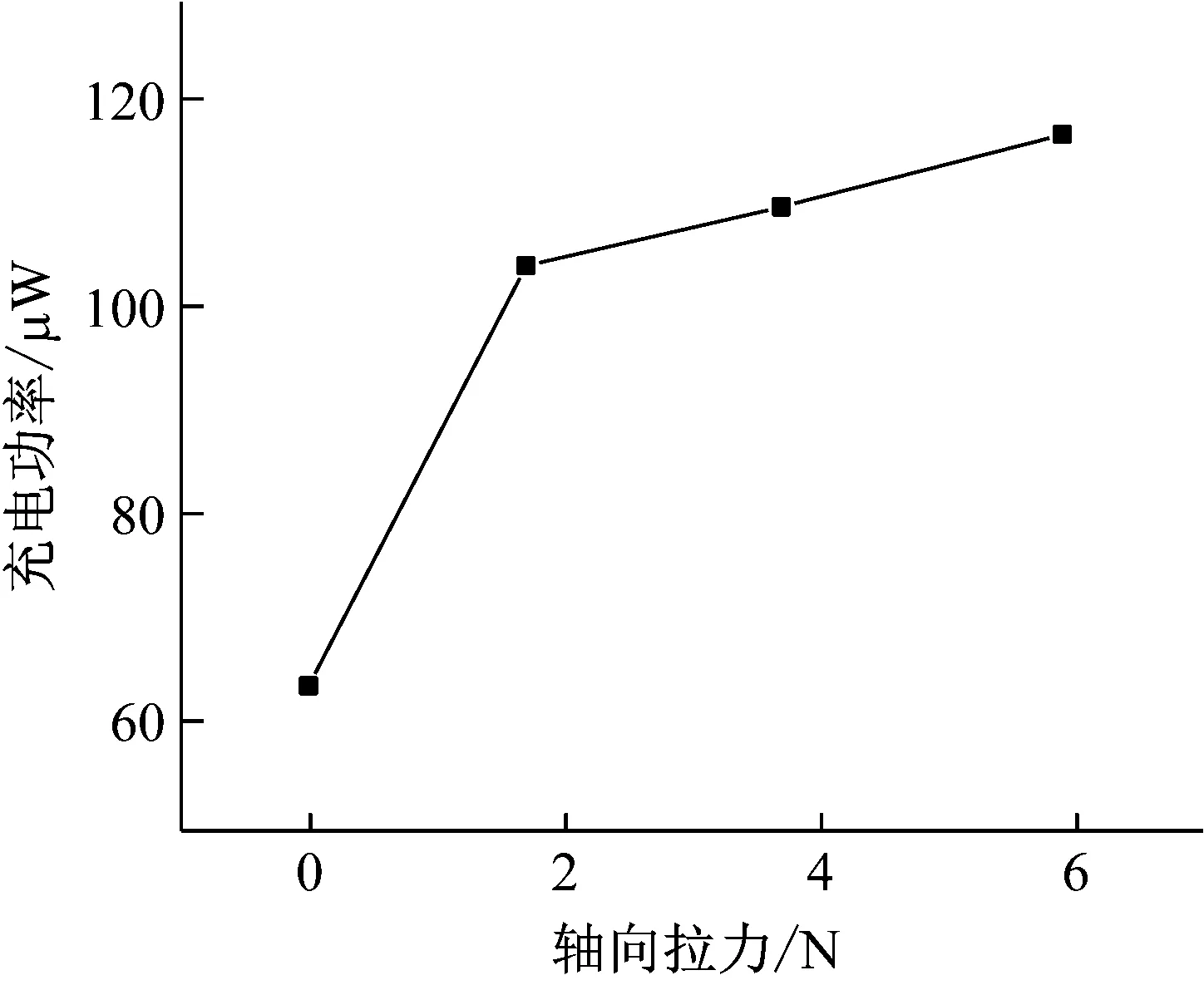
图15 不同轴向拉力下的平均充电功率曲线图

4 结 论

本文设计了一种基于预应力梁的压电式能量采集器，并进行了数学建模仿真和相关试验测试。试验结果表明，轴向拉力作用下使压电能量采集器的固有频率发生偏移。此外，在相同的加速度激励条件下，与传统压电能量采集器相比，预加载轴向力增大了压电能量采集器的共振频率，提高了开路状态下的电压峰值，电容充电试验中也有良好表现，实现了更好的能量收集应用。与无轴向张力的压电能量采集器相比，5.9 N初始轴向拉力作用下平均充电功率提高了83.1%。通过该压电能量采集器模型的分析，可以通过在传统压电能量采集器的末端施加预应力提高能量采集效率。