基于人工神经网络的椭圆型微分方程数值求解

袁冬芳, 刘文慧, 崔桂梅, 石 琳

(1.内蒙古科技大学 理学院，内蒙古 包头 014010; 2.内蒙古科技大学 信息工程学院，内蒙古 包头 014010)

微分方程被广泛应用于各个领域的建模过程中[1—2]，尤其在工程、数学、物理学、经济学等领域，许多问题最终都可归结为微分方程的求解.常用的数值求解方法有Runge-Kutta方法、线性多步法和预测校正法等[3—5]，有限差分、有限元等相关方法[6]也为求解微分方程提供了一种思路.但传统的求解方法对于高维问题和复杂区域的偏微分方程，通常表现出收敛性的证明过程较繁琐、计算量大、求解时间长等缺点，因此，研究人员也在不断尝试求解偏微分方程的新方法和工具.

多年来，神经网络逐渐由单个感知器发展成多层的深度神经网络，在图像识别、自然语言处理、认知科学等领域得到了广泛的应用[7—9].一方面，由逼近理论[10—11]得知，足够复杂的神经网络能够无限逼近任意非线性函数.因此，神经网络可以作为一个强有力的函数逼近器[12].鉴于微分方程的解通常是非线性函数，故利用神经网络求解微分方程不失为一个新的尝试.另一方面，由于神经网络解的偏导数可以用自动微分法以封闭性形式求出，故可以表示任何偏微分方程.

人工神经网络(ANN)的概念起源于20世纪40年代，Warren McCulloch 和 Walter Pitts提出了基于数学和算法的ANN计算模型，此模型被称为M-P模型.经过多年的发展，Paul Werbos[13]提出了反向传播算法，该算法有效解决了单层神经网络只能处理异或问题的局限性，从而使得多层神经网络有一种可训练的能力.21世纪神经网络的研究走向成熟，由最初简单的神经元感知器衍生出一系列的神经网络，主要有BP神经网络、Hopfied神经网络、RBF神经网络、卷积神经网络等.BP神经网络具有很强的非线性映射能力，用BP神经网络训练得到微分方程的近似解，当问题维数增大时，计算量增加相对较小，克服了传统方法求解微分方程的缺点.

1 神经网络及其结构

神经网络主要由输入层、隐藏层和输出层3个结构组成，其中神经元是网络的基本结构(图1).神经网络的隐藏层可以有多层结构，每一层由若干个神经元组成.

一般来说，如果神经网络有足够的隐层单元，此时多层神经网络可以逼近任何非线性函数.如果神经元的激活函数使用sigmoid函数，单个神经元的输入和输出满足

y=sigmoid(wx+b)，

其中：w为权值；b为阈值.

图1 单层神经网络结构

由于多层网络结构的复杂性，在实际操作中一般使用矩阵形式表达网络的输入与输出关系.由单个神经元的输入与输出关系，可推导出多层神经网络的输入与输出的矩阵形式(以一个两层神经网络为例):

N(X)=sig(sig(XTW(1)+B(1))W(2)+B(2))W(3)，

其中W(1),W(2),B(1),B(2),W(3)分别表示第一、第二隐藏层神经元的权值，第一、第二隐藏层神经元的阈值以及输出层的权值.

神经网络结构搭建成功后，用训练集对模型进行优化训练.给定训练集D={(x1,y1),(x2,y2),…,(xm,ym)},令神经网络的输出为N=(n1,n2,…,nm).一般用均方差函数刻画神经网络模型和训练集的误差,其计算公式为

其中:nk为网络输出;yk为训练集数据;Lossk(k=1,2,…,m)为误差.

神经网络模型与真实值之间的误差是关于W,B的函数，通过调节W,B的值缩小两者之间的差距.常用梯度下降法对神经网络进行优化，优化的过程实质就是对权值和阈值沿着误差函数下降最快的方向——负梯度方向进行调整.权值和阈值的更新公式为

wt=wt-1+Δw，

(1)

其中wt中wt-1分别代表神经网络第t次和第t-1次的学习权值，对于阈值调节和权值调节方法类似.

神经网络每次调整权值和阈值增量的方法为

(2)

(3)

其中:wjk和bjk指的是隐藏层的第j个神经元和输出层第k个神经元之间的连接权值和阈值;η是学习率，需要人为设定.

2 神经网络求解微分方程

n阶微分方程的一般形式定义为

G(x,Ψ(x),∇Ψ(x),∇2Ψ(x),…,∇nΨ(x))=0，其中微分方程的解还受到边界条件B.Cs的限制.

鉴于神经网络强大的非线性映射能力，研究人员通过建立一套学习规则调节网络的参数W和B，从而利用神经网络学习方程的解.早期的损失函数[14—16]主要由2项组成：①微分方程的真解和训练模型的误差，记为LossMSE,D；②边界条件的误差惩罚项，记为LossMSE,B.Cs，其构造如下：

Loss=LossMSE,D+LossMSE,B.Cs，

其中

LossMSE,D=mean(G(x,N,∇N,∇2N,…,∇nN)-

G(x,Ψ,∇Ψ,∇2Ψ,…,∇nΨ))2，

LossMSE,B.Cs=mean((N(xB.Cs)-Ψ(xB.Cs))2+

(∇N(xB.Cs)-∇Ψ(xB.Cs))2+

(∇2N(xB.Cs)-∇2Ψ(xB.Cs))2+…+

(∇nN(xB.Cs)-∇nΨ(xB.Cs))2).

Loss函数构造完成后，利用(1)～(3)式进行权值和阈值更新，完成对模型的学习.

3 数值算例

算例1考察二阶常微分方程

x∈[0,2].

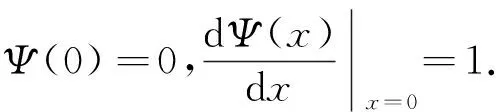
通过网络的训练和学习可知，训练集的误差在10-3以内(图2).但仅通过训练集的误差对比不能充分说明神经网络模型求解的优越性，故将方程的解析解与训练模型的一阶导数及二阶导数分别进行对比(图3)，可以看到结果十分吻合.在神经网络的求解过程中可以观察到微分方程的任意阶导数，这在工程领域研究中往往是有需要的.同时从测试集的计算结果及误差(图4)可以看到，利用神经网络方法求解微分方程不失为一种好的尝试.

a训练集结果对比

b误差分析图2 算例1训练集结果对比及误差分析

a一阶导数

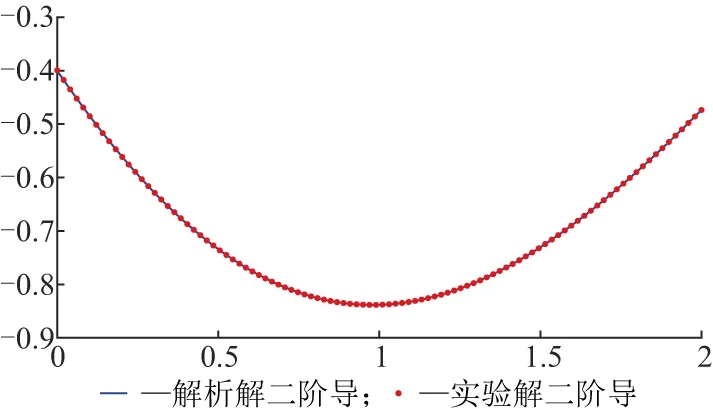
b二阶导数图3 算例1解析解与训练模型一阶导数及二阶导数对比

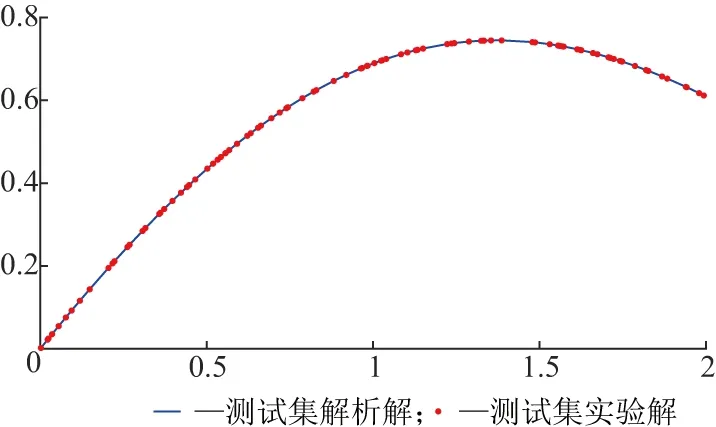
a测试集结果对比

b测试集误差分析图4 算例1测试集结果对比及误差分析

耦合方程常用来描述微波学、激光学和热力学等问题.由于传统的数值求解方法计算量大且精度较低，阻碍了相关问题的研究进度.受前2个算例启发，利用神经网络求解耦合方程不失为一种新思路.一阶耦合的微分方程一般定义为

算例2考察耦合方程

x∈[0,2]，

x∈[0,2].

方程的解析解为Ψ1(x)=sinx,Ψ2(x)=1+x2，边界条件为Ψ1(0)=0,Ψ2(0)=1.

利用神经网络求解该方程，由训练集计算结果及误差分析(图5)和测试集计算结果及误差分析(图6)可知，用神经网络模型逼近耦合方程的解，误差平均在10-3以内.

边界对流扩散方程的数值解是流体力学和气体动力学的研究问题之一.这类方程与众不同的特点是在边界的数值变化十分剧烈，因此，常规的数值求解方法较难求出方程的解析解.同时，在传统的神经网络模型学习过程中由于边界变化剧烈，导致求解结果与真实解相差甚远.针对这种情况，选择一种新的构造训练解的方法：

即把方程的求解模型分为边界条件A(x)和对应微分方程F(x)N(x).

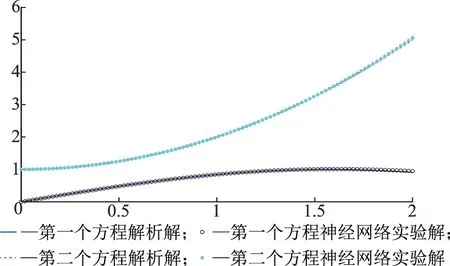
a训练集结果对比

b误差分析图5 算例2训练集结果对比及误差分析

a测试集结果对比

b误差分析图6 算例2测试集结果对比及误差分析

算例3考察一维对流扩散方程

该问题在右边界层具有很大的跳跃性.实际训练模型构造如下：

(x-0)(x-1)N(x),

最后利用梯度下降法学习模型，结果见图7和图8，可以看到计算结果吻合程度比较高，误差平均值均在10-3以内.

a训练集结果对比

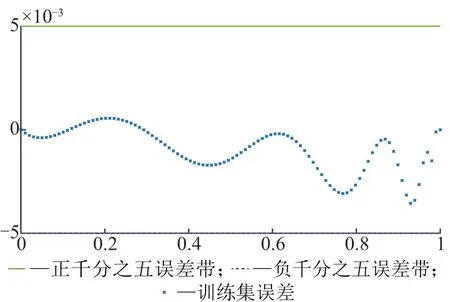
b误差分析图7 算例3训练集结果对比及误差分析

a测试集结果对比

b误差分析图8 算例3测试集结果对比及误差分析

算例4考察二维偏微分方程

边界条件为ψ(0,y)=y3,ψ(1,y)=(1+y3)e-1,ψ(x,0)=xe-x,ψ(x,1)=e-x(x+1).定义区间[0,1]×[0,1]，方程的解析解为ψ(x,y)=e-x(x+y3).

在定义区间内均匀选择20×20个网格点训练模型，测试集均匀选择45×45个网格点，得到测试集解析解与数值解结果(图9～图10)，误差分析截面数据见图11，可以看到用神经网络求解效果非常理想.

图9 测试集解析解

图10 测试集神经网络实验解

图11 测试集截面误差分析

4 结论

神经网络方法为求解椭圆型微分方程开辟了一条有效的新途径. 一方面，针对椭圆型微分方程，经过神经网络训练的模型，不仅具有较高的精度，还可以得到解的任意阶导数，同时计算量较小，速度较快，具有良好的泛化性. 另一方面，神经网络方法求解复杂微分方程的收敛性和计算效率尚且需要进一步提高和改进.因此，需要进一步探索神经网络方法的性能，研究出更普适、高效的求解方法.