发动机平衡轴壳体结构分析及优化

祝慧敏，付景顺，乔赫廷

（沈阳工业大学机械工程学院，辽宁 沈阳 110870）

1 引言

作为最常用的汽车动力装置，四缸直列式发动机内部惯性力系中力及力矩的不平衡，是发动机产生振动和噪声的重要原因。对发动机的振动平衡分析得出，不平衡的二阶往复惯性力是产生振动的主要原因之一[1]。而四缸机又无法依靠自身的平衡或曲轴上的平衡重来消除二阶往复惯性力的影响，因此，现在开发的发动机一般都通过安装平衡轴总成来最大限度的降低发动机的运转不平衡。但在实际应用过程中，某配备平衡轴总成的发动机在第20h台架试验时出现异响，拆解后发现平衡轴壳体出现断裂，因此需对壳体断裂问题进行专项研究。

目前，针对壳体断裂问题，文献[2]对某断裂平衡轴壳体进行了模态分析，确定壳体断裂原因为壳体刚度不足，通过反复修改模型加筋部位及断裂部位的结构来解决断裂问题。文献[3]对某断裂变速箱壳体，以经验公式计算得到的壳体受力为边界条件，进行了强度分析，确定壳体断裂原因为壳体材料强度不足，通过使用高抗拉强度的材料替换原始材料来解决断裂问题，但通过多次公式近似计算得到的壳体受力并不准确且材料替换后壳体质量有了显著增加。文献[4]对某断裂差速器壳体进行了失效模式分析和静强度分析，确定壳体断裂原因为换挡过程的交变载荷引起的疲劳失效，但并未给出一种可行、高效的方法来解决壳体断裂问题。

针对壳体总成断裂原因多样性和现有研究的不足，这里基于建立的平衡轴总成三维模型，对总成进行模态、强度和疲劳分析来确定壳体断裂原因，采用一种基于精英保存策略，引入快速非支配排序思想的遗传算法对壳体结构进行优化来解决壳体断裂问题。

2 平衡轴总成模态分析

平衡轴总成结构主要包括：主、从动平衡轴，齿轮，滑动轴承，轴承盖和上、下壳体。

壳体和平衡轴通过滑动轴承有机结合。平衡轴总成通过螺栓连接固定在气缸体底部。对添加完材料特性的平衡轴总成几何模型划分网格建立其有限元模型，材料属性，如表1所示。

表1 各部件材料属性Tab.1 Material Properties of Each Component

在平衡轴总成与气缸体底部进行螺栓连接的螺栓孔位置添加固定约束作为边界条件，对其进行模态分析，提取前六阶模态频率，如表2所示。

表2 前六阶模态频率Tab.2 1~6 Order Modal Frequencies

平衡轴壳体受力主要为平衡轴不平衡重产生的旋转惯性力，因此，平衡轴总成的固有频率不能与平衡轴的工作频率[2]相同或相近，平衡轴的工作频率为：

式中：n—平衡轴转速。

发动机进行台架试验时的曲轴转速为6000rpm，平衡轴与曲轴的传动比为2：1，可知平衡轴转速为12000rpm，工作频率为400Hz。

对比平衡轴总成的前六阶模态频率和平衡轴的工作频率可知，平衡轴总成模态频率与平衡轴的工作频率不相近，没有共振现象的发生，且平衡轴总成的模态频率大于平衡轴的工作频率[5]，因此，排除壳体是由于刚度不足，模态频率低而发生断裂。

3 平衡轴壳体强度分析

3.1 平衡轴总成多体动力学分析

平衡轴壳体受力主要为平衡轴旋转产生的惯性力，旋转惯性力通过滑动轴承作用在壳体轴承孔上。对平衡轴总成进行多体动力学分析，获得由滑动轴承传递给壳体的惯性力。

对平衡轴总成的三维模型添加材料属性并进行约束建立其多体动力学模型。

各部件约束，如表3所示。

表3 各部件约束Tab.3 Constraints of Each Component

根据平衡轴转速对平衡轴主动轴添加角速度为72000°/s的驱动。壳体受力分析结果，如图1所示。a、b为主动平衡轴左、右两侧轴承孔的x、y、z方向受力，c、d为从动平衡轴左、右两侧轴承孔的x、y、z方向受力，负值表示与坐标系正向相反。

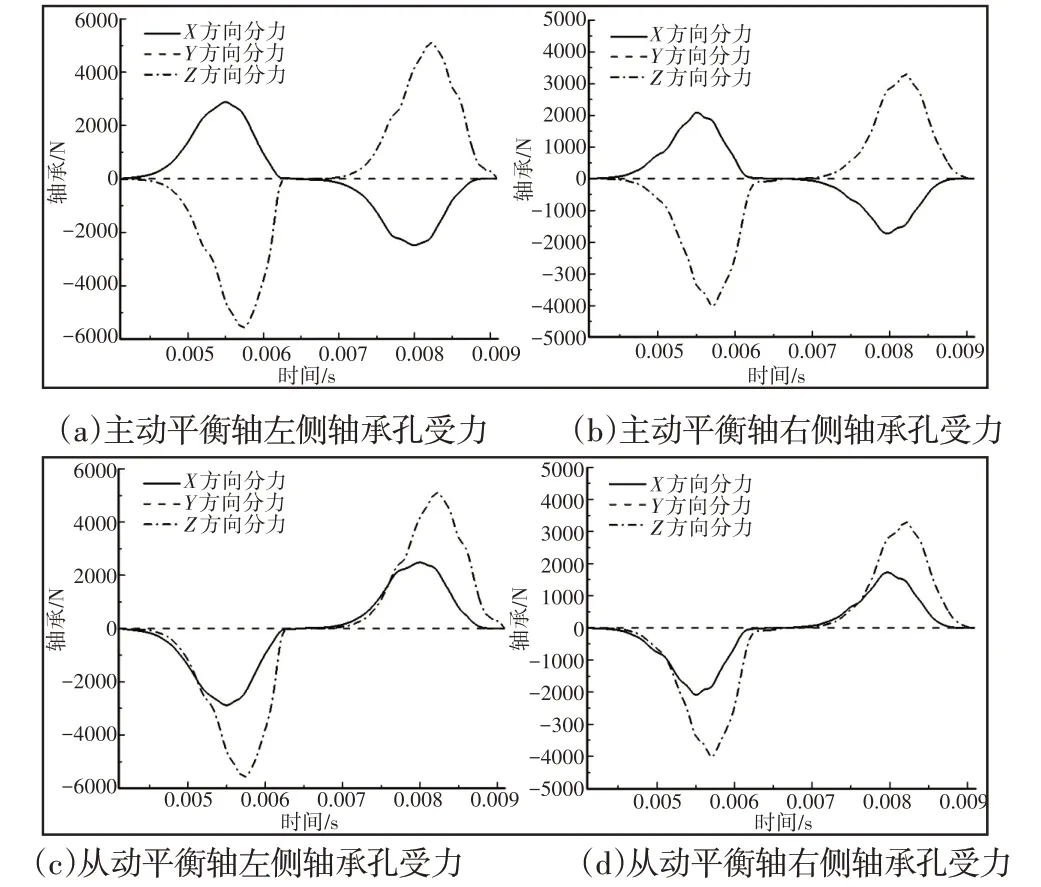
图1 壳体受力分析结果Fig.1 Shell Force Analysis Results

由图1可知，主、从动平衡轴同侧轴承孔x方向受力大小相等，方向相反，y方向受力接近于0。选取轴承孔x和z方向受力分别取得最大值的四个时刻0.0055s、0.0057s、0.008s、0.0082s进行平衡轴壳体强度分析。

3.2 平衡轴壳体强度分析

由轴承传递给壳体的惯性力产生的压力载荷分布在壳体孔的圆周表面上，压力载荷呈余弦规律分布在轴承孔圆周表面120°范围内[6]，如图2所示。

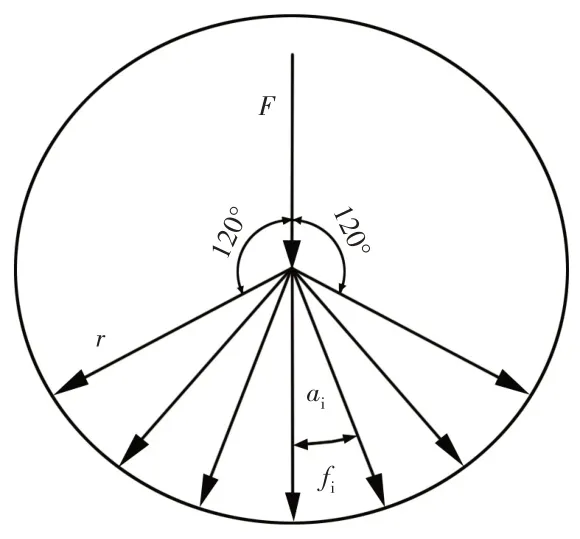
图2 轴承孔径压力受力图Fig.2 Bearing Aperture Pressure Force Diagram

压力载荷的分布函数为：

式中：F—壳体受力；r—轴承孔半径；t—滑动轴承宽度；αi—压力载荷fi与壳体受力F的夹角。

将多体动力学分析得到的平衡轴壳体受力按照压力载荷的分布函数加载到壳体轴承孔上，并在螺栓孔位置添加固定约束进行强度分析，得到四种加载工况的等效应力云图，如表4所示。

表4 最大等效应力及等效应力云图Tab.4 Maximum Equivalent Stress and Equivalent Stress Cloud Map

由四种加载工况的等效应力云图可知，最大应力分布位置均在平衡轴上壳体左下方的螺栓孔位置，与平衡轴壳体在进行发动机台架试验时出现断裂的位置一致，验证了模型建立和强度分析的正确性。对比四种加载工况的最大等效应力值，发现0.0057s时刻的最大应力值最大，为181.66MPa，低于壳体材料YL113的抗拉强度228MPa，排除壳体是由于抗拉强度不足发生断裂。因此，初步判断平衡轴壳体断裂原因为重复加载引起的应力疲劳失效。

4 平衡轴壳体疲劳分析

平衡轴壳体材料为YL113，对YL113材料的光滑标准试件进行疲劳试验得到YL113材料S−N曲线。由于平衡轴壳体结构的形状、尺寸和表面粗糙度等与试验过程中使用的YL113光滑标准试件均有差异，设定疲劳强度因子对YL113材料的S−N曲线进行修正，获得平衡轴壳体的S−N曲线。应用平衡轴总成多体动力学分析获得的壳体受力−时间历程作为疲劳载荷谱进行平衡轴壳体疲劳分析。疲劳分析结果，如图3所示，疲劳寿命云图，图3（a）所示。安全系数云图，如图3（b）所示。

由图（a）可知，最小寿命在平衡轴上壳体左下方的螺栓孔位置，与壳体台架试验时断裂的位置一致。最小寿命为（1.4793×107）个循环，由平衡轴转速可知一个载荷循环的时长为0.005s，计算可得平衡轴壳体的最小寿命约为20.55h，与壳体在进行台架试验时发生断裂的时间基本一致。因此，进一步确定平衡轴壳体的断裂原因为重复加载引起的应力疲劳失效。

安全系数是综合考虑材料缺陷，工作偏差等不定因素，为保证结构承受的力大于许用应力而引入的参数，定义为极限应力与许用应力的比值，必须大于1[7]。

由图3（b）可知，最小安全系数在平衡轴上壳体左下方的螺栓孔位置，与平衡轴壳体发生断裂的位置一致。最小安全系数为0.74739，小于1，不符合工作需求。

图3 疲劳分析结果Fig.3 Fatigue Analysis Results

材料力学研究表明，机械结构疲劳寿命的影响因素主要包括：机械结构的工作条件、结构的几何形状及表面状态、结构的材料、结构的表面加工方法等[8]，考虑平衡轴壳体为整体压铸铝合金结构，断裂位置在螺栓孔部位，因此，解决壳体断裂问题较为高效、经济的方法为优化壳体断裂部位的几何尺寸。

5 平衡轴壳体结构优化

5.1 优化模型建立

根据设计要求，发动机要保证连续600h无故障台架耐久试验，即平衡轴壳体的疲劳寿命要达到600h，约为（4.32×108）个循环。为保证平衡轴壳体结构承受的力大于许用应力，最小安全系数要大于1。在确保平衡轴壳体疲劳寿命满足要求，不再发生断裂的条件下，要避免其质量的大幅度增加。因此，选取平衡轴壳体的最小疲劳寿命、最小安全系数和质量作为壳体结构优化的目标函数。

要确保壳体的最大应力值低于壳体材料YL113的抗拉强度228MPa。因此，选取平衡轴壳体的最大应力值作为壳体结构优化的状态变量。

初步选取壳体断裂部位直径、高度和加强筋厚度作为壳体结构优化的设计变量。通过分析各目标函数对设计变量的敏感性来对设计变量进行选择，分析结果，如图4所示。使优化效率得到显著提高[9]。

图4 局部灵敏度分析Fig.4 Local Sensitivity Analysis

从图5 可知，各目标函数对断裂部位直径的变化反应不灵敏，而对断裂部位高度和加强筋厚度的变化具有较灵敏的反应。因此，最终选定断裂部位高度和加强筋厚度作为壳体结构优化的设计变量。

综合考虑壳体的结构尺寸和安装尺寸，并避免原始结构的较大改动，初步确定一个设计变量的取值范围。在此范围内，应用中心复合实验设计法选取样本点生成克里格响应曲面，通过响应曲面分析在全局最优解附近选取设计变量，使设计变量的取值范围缩小，得到更高的优化精度[10]，分析结果，如图5所示。

图5 响应曲面分析Fig.5 Response Surface Analysis

从图6可知，加强筋厚度取值为3mm，3.3mm，3.45mm时，最小疲劳寿命取得最大值；断裂部位高度在（18~22）mm之间时，最小疲劳寿命取得最大值。因此，最终选定设计变量加强筋厚度的取值范围为（3~3.6）mm，断裂部位高度取值范围为（18~22）mm。

建立壳体结构优化模型为：

式中：P1，P2—分别设计变量加强筋厚度和断裂部位高度；

P3，P4和P5—分别目标函数最小疲劳寿命，最小安全系数和质量；

P6—状态变量平衡轴壳体的最大应力值。

5.2 优化求解

采用基于精英保存策略，引入快速非支配排序思想的第二代非支配分类遗传算法对壳体结构进行多目标优化优化[11]。其算法流程为：

（1）随机生成大小为N的初始父代种群，应用快速非支配排序思想对种群进行排序，然后选择优秀的父代种群个体进行交叉和突变，产生新的后代种群。

交叉和突变是生成新种群的两个主要步骤，根据以下等式线性组合两个父代染色体载体以产生两个新后代种群个体：

根据下述多项式来实现变异：

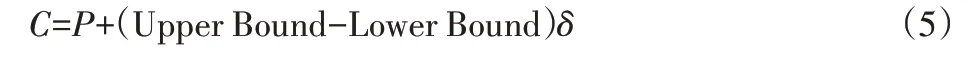
式中：C—变异产生的新的子代种群个体；P—优秀父代种群个体；δ—变异算子。

（2）合并父代种群和产生的后代种群，得到大小为2N的新的后代种群。应用快速非支配排序思想对种群进行排序和个体拥挤度计算，采用精英保存策略产生新的父代种群。

（3）应用快速非支配排序思想对新一代的父代种群进行排序，然后选择优秀的父代种群个体进行交叉和突变，再产生新的后代种群，依此法不断循环[12]，直到达到最大进化代数，算法结束。

平衡轴壳体的最终优化结果，如图6所示。得到三个符合目标函数约束条件的候选点，从图中可以看出，候选点1的最小疲劳寿命和最小安全系数取得最大值，候选点2、3质量较小。

图6 结构优化结果Fig.6 Structural Optimization Result

5.3 优化结果验证

参考优化结果提供的候选点，综合平衡轴壳体为压铸结构，不会出现优化结果中的小数点后四位情况，选取加强筋厚度P1值为3.3mm，断裂部位高度P2值为21.5mm建立新的三维模型，对优化后的结果进行验证，验证结果，如图7所示。

图7 优化结果验证Fig.7 Optimization Result Verification

由等效应力云图可知，应力最大值仍然在壳体优化前发生断裂的部位，但优化后应力最大值为127.92MPa，低于优化前的181.66MPa。

由疲劳寿命云图可知，平衡轴壳体的整体疲劳寿命为5×108个循环，计算可得疲劳寿命为694h，满足发动机要保证连续600h无故障台架耐久试验的要求。由安全系数云图可知，安全系数最小值可达1.0349，满足壳体的最小安全系数须大于1 的要求[8]。

平衡轴壳体结构优化前后的参数对比数据，如表5所示。虽然优化后壳体质量有了小幅增加，但各项指标均得到优化，解决了平衡轴壳体的断裂问题。

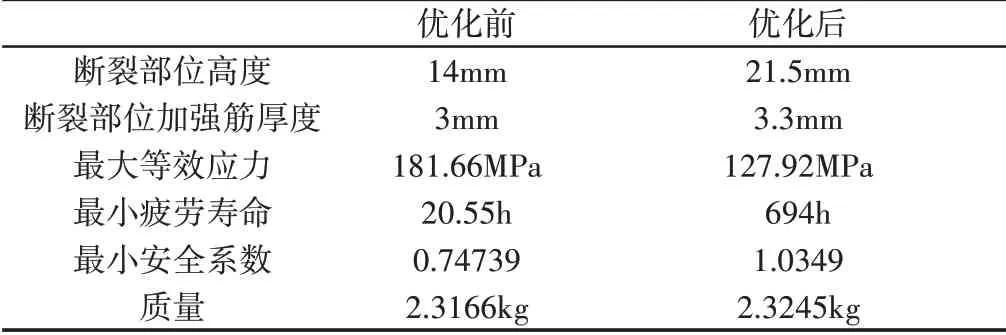
表5 优化前后参数对比Tab.5 Comparison of Parameters Before and After Optimization

6 结论

（1）针对发动机平衡轴壳体断裂问题，在建立的平衡轴总成几何模型基础上，对平衡轴总成进行了模态分析，排除壳体是由于刚度不满足要求而引起断裂。

通过对平衡轴总成进行多体动力学分析获得壳体受力，解决了通过多次公式近似计算得到的壳体受力并不准确的问题，在此基础上，对壳体结构进行了强度分析，排除壳体是由于抗拉强度不足而引起断裂。最终通过疲劳分析确定了壳体断裂原因为平衡轴旋转惯性力重复加载造成的应力疲劳失效。

（2）在断裂原因分析的基础上，首次采用第二代非支配排序遗传算法对出现断裂问题的平衡轴壳体结构进行了多目标优化，得到了壳体断裂部位的最佳尺寸，优化结果验证表明，该方法在保证壳体结构较小改动、壳体质量较小增加的基础上，有效地提高了壳体的疲劳寿命，解决了平衡轴壳体的断裂问题。

（3）基于第二代非支配排序遗传算法的多目标优化方法，可以快速得到符合多个目标函数的最优结果，缩短优化周期，降低优化成本，为解决工程实际问题中机械结构原始断裂问题提供了一种可行、高效的思路。