高压导管球形接头结构密封性能研究

宋瑞宏，戴忞中，史文杰，王剑锋

（1.常州大学机械工程学院，江苏 常州 213164；2.常州市模具先进制造高技术研究重点实验室，江苏 常州213164；3.江苏腾驰科技有限公司，江苏 常州 213165）

1 引言

目前，发动机安全性能发展受到阻碍的原因之一就是内泄漏问题，而高压导管接口处泄漏发生率占整个系统泄漏的50%以上。因此，高压导管的密封性能是评价汽车发动机安全性的重要指标，预防接口泄漏是治理系统泄漏的重要环节。发动机运行过程中发生工作介质的泄漏，不仅会影响发动机的工况，还可能会对人身造成伤害。球面−锥面密封结构作为现阶段新型混合动力汽车发动机常用导管连接形式，具有较高的密封性能，同时方便拆卸，便于维护保养后二次使用。为了保证高压导管球形接头处的密封效果，许多学者对高压导管球形接头结构的密封性能进行了研究。

文献[1]根据Roth模型，提出了对球面−锥面密封结构进行漏率预估的方法，利用有限元计算得到拧紧力矩与密封面宽度和密封面平均接触应力的关系，然后代入漏率预估公式进行计算，然而该方法使用的Roth模型仅定义两个表面压紧形成的密封面，对研究球面与锥面压紧形成的密封面而言存在一定缺陷。文献[2]考虑了应力松弛现象对球面−锥面密封结构漏率的影响并进行了分析，给出松弛模型，对准确定量预估密封结构具有重要意义，但减少应力松弛现象的措施还有待改进。文献[3]运用有限元分析研究了球面−锥面密封结构的密封性能，选取不同的结构参数分别分析计算，给出了影响密封性能的各项指标，由于未进行实验验证，得到的数据准确性可能存在偏差。

根据以上分析，提出使用漏率经验公式并结合Hertz接触理论对球面−锥面密封结构泄漏进行预估，配合有限元分析的结果研究球面−锥面密封结构的密封性能，提供高压导管合适的安装扭矩作为指导，最后结合实验结果验证研究的可行性与数据的准确性。

2 泄漏计算

2.1 密封机制

高压导管在球形接头处的球面−锥面密封结构示意图，如图1所示。球形接头的球面与扩口式接头锥面在安装配合初始阶段是线性接触的，在对锁紧螺母施加一定力矩后，球面与锥面接触部分会因受力产生变形，从而变成非线性接触，形成一个环状的密封面。

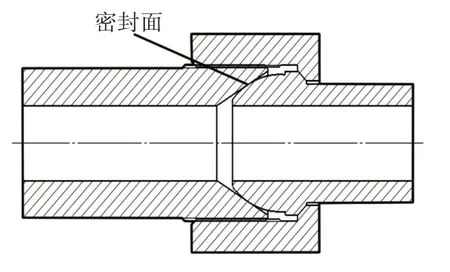
图1 球面−锥面密封结构示意图Fig.1 Sphere−Cone Sealing Structure

2.2 泄漏模型

A Roth等认为：在密封面拥有一定粗糙度的情况下，球面−锥面密封结构的密封面上存在着形状为等腰三角形的微型漏孔，这些三角形漏孔的横截面积恒定，在密封面上呈并联排布，流体在这种微型漏孔中流动时表现为分子流。球面−锥面密封结构在检漏条件下的设计总漏率应小于1×10−6Pa·m3/s，所以单个微型漏孔的漏率必定远小于气流处于分子流状态时的漏率1×10−7Pa·m3/s，故将这里单个漏孔泄漏的流体状态认定为分子流状态[4]。

根据文献[5]可知漏孔流体在分子流状态下有漏孔流导计算公式为：

式中：K—漏孔通道形状系数；A—漏孔流道的截面积；

B—包围流道面积A的周界；

L—漏孔的长度；

W—密封面的宽度。

A Roth指出密封面上构成的微型漏孔横截面典型形式是底角α=4°的等腰三角形，取α=4°，此时K=1.7。在等腰三角形漏孔通道中，由高为h，底为l，可得：

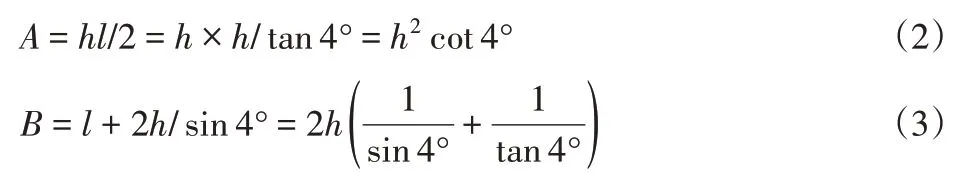
式中：R—通用气体常数；T—气体绝对温度；m—气体分子质量。

将式（2）~式（4）代入到式（1）可计算对于单个横截面为等腰三角形的漏孔流道的流导为：

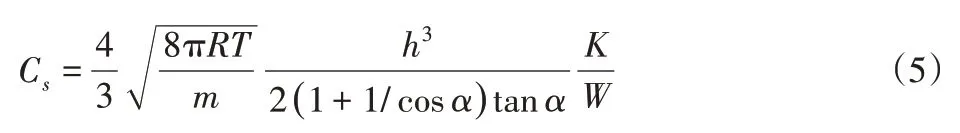
球面—锥面密封结构的密封面是直径为D的密封环，其密封面上漏孔个数可通过几何关系得出：

式中：H—初始微型漏孔底边上的高。

因此，可以得出整个密封面的总导流为：

根据文献[6]

式中：σm—密封面平均接触应力；Ks—密封面材料的密封性能系数。

根据Hertz接触理论[7]，以球面与锥面接触面中心点为坐标原点，沿锥面方向的切向和球面径向的法向作为x、y轴建立直角坐标系xoy，球面与锥面接触形成的密封面法向接触应力可表达为：

式中：E*—当量弹性模量；Ws—密封面接触半宽；Rs—球面半径。

从而，密封面平均接触应力为：

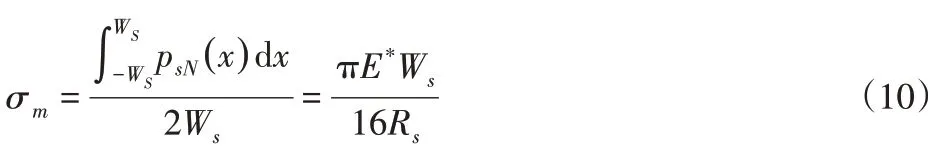
由此可推出球面−锥面密封结构的总漏率为：

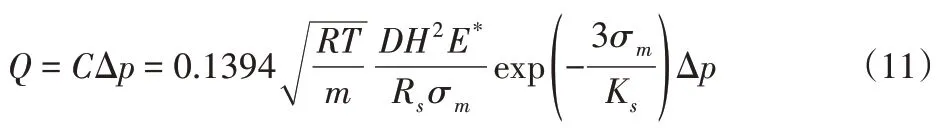
2.3 漏率数值

对实际工作中安装条件下的导管连接件选取常温氦气进行漏率计算，可取各参数值为：T=293K，m=4，R=8314.4，D=9.3923mm，H=0.8μm，E*= 222.44GPa，Rs=6mm，Ks=30MPa，为了更直观的表现接触应力与漏率的关系，对总漏率公式取对数，将上述数值代入式（11）计算能够得到漏率随密封面接触应力变化的曲线，如图2所示。

检漏条件下高压导管接头处于密封状态的总漏率应小于1×10−6Pa·m3/s，根据图2可知在密封面接触应力达到122.5MPa时满足密封条件，考虑内压达到20MPa的情况，密封面接触应力需略增大至133.4MPa，因此，导管材料304不锈钢处在弹性变形阶段时即可实现密封功能。同时可以看出，拧紧力矩的增加使密封面宽度与接触应力增加，密封效果越好。但密封面长时间保持恒定变形容易产生应力松弛现象[2]，所以每隔一段时间需要检漏维护，减少因应力松弛发生塑性变形与应力减小导致密封性能下降的情况。

图2 总漏率随密封面平均接触应力的变化关系Fig.2 Relationship Between Leakage Rate with Sealing Surface Average Contact Stress

3 球面−锥面密封结构有限元模型

以导管连接接头球面−锥面为研究对象，考虑到球面−锥面接触后环状密封面宽度和接触应力影响着泄漏率，需要研究安装过程中拧紧力矩与两者之间的对应关系。球面和锥面在受力产生变形后逐渐形成密封面，过程中接触区域发生了弹塑性变形，因此，对球面−锥面的分析属于接触分析和弹塑性分析并存，这两者都是高度的非线性问题。接触分析中的边界约束条件需要找到精确的拉格朗日乘子，这里使用罚函数进行修正迭代的方法实现。金属材料弹塑性分析的模型种类较多，考虑实际材料特性后，采用适用于无循环加载情况下的双线性等向强化模型实现求解[8−9]。对所研究的高压导管球形接头结构进行建模分析，由于高压导管整体结构是轴对称结构，这里可以只对其二维剖面网格划分，选择使用二维轴对称单元PLANE82，网格划分同时对接触区域进行细化，提高分析精度，网格划分后的有限元模型，如图3所示。

图3 接头网格划分有限元模型Fig.3 Joint Meshing Finite Element Model

根据接触分析原则，在球面和锥面以及球形接头和锁紧螺母间分别选取接触单元TARGE169和CONTA172建立接触对。在实际装配过程中可控制输入量是拧紧力矩，有限元分析是通过在锁紧螺母截面添加预紧力单元PRETS179来施加预紧力作为输入量，预紧力可由施加的拧紧力矩换算出，根据文献[10]可知换算公式为：

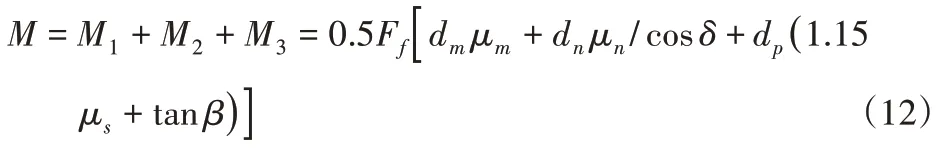
式中：Ff—螺纹连接预紧力；dm—球头−螺母接触面圆环宽度；μm—球头−螺母接触面摩擦因数；dn—球面−锥面接触面圆环宽度；μn—球面−锥面接触面摩擦因数；δ—扩口式锥面倾角；dp—外螺纹有效直径；μs—螺纹副摩擦因数；β—螺纹升角。

4 计算结果与分析

4.1 密封面平均接触应力

经过有限元计算，把接触面离散为接触单元，可以计算出各接触单元的接触应力和接触距离，通过统计有效接触单元的相关参量数据，就能够得到密封面平均接触应力、密封面宽度和密封区域接触应力分布这些重要指标来考核密封面实际密封性能[11]，因此，分析拧紧力矩与这些指标之间的对应关系对研究密封性能而言十分重要。

密封面平均接触应力与拧紧力矩对应关系曲线，如图4 所示。从图中可以看出，随着拧紧力矩的不断增加，密封面平均接触应力也不断增加，这样会使球面−锥面结构的密封连接更加紧密，降低密封结构总漏率，所以密封面平均接触应力可作为结构密封性能的评价标准。从曲线增长速率可以看出平均接触应力的增加速率是以逐渐减缓的增长方式在增加的，应力增速的减缓可以避免接触面因应力增长过快而造成损伤，使接触面保持在相对安全的应力范围内。在拧紧力矩达到18.8N·m时，密封面平均接触应力为204.9MPa，接头球面与锥面接触部分达到材料屈服极限205MPa，因此，在保证导管密封性能且不影响二次使用情况下，合适的安装扭矩大小应接近且不超过18.8N·m。

图4 拧紧力矩−密封面平均接触应力Fig.4 Tightening Torque−Average Contact Stress of the Sealing Surface

4.2 密封面宽度

经有限元计算，球面与锥面经挤压所形成的接触面是一个轴对称的圆环形斜面，圆环间距就是密封面宽度，密封面宽度与拧紧力矩对应关系曲线，如图5所示。从图中可以看出密封面宽度与拧紧力矩近似于恒定正比例关系，密封面宽度以恒定斜率直线增加。由漏孔流导计算式（1）可知密封面越宽，密封效果相对越好，因此拧紧力矩的增加可以使密封结构拥有更好的密封性能。

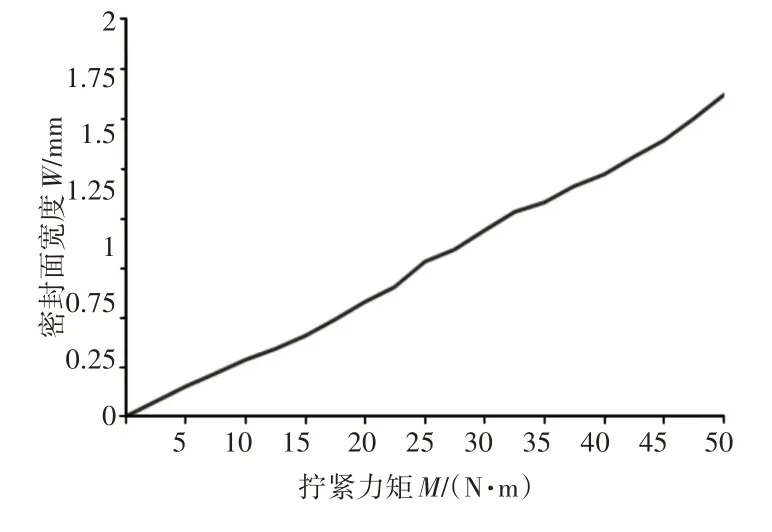
图5 拧紧力矩−密封面宽度Fig.5 Tightening Torque−Sealing Surface Width

在一定范围内，密封面平均接触应力与密封面宽度的增加都对密封性能起着正面作用，锁紧螺母拧紧过程中，两者同时增加能够快速增强密封结构的密封性能，达到密封状态。拧紧力矩为18.8N·m时的密封面，此时密封面宽度为0.56mm，如图6所示。

图6 拧紧力矩18.8N·m时的密封面Fig.6 Sealing Surface with Tightening Torque of 18.8N·m

4.3 密封区域接触应力分布

拧紧力矩为18.8N·m时密封区域的接触应力，如图7所示。因为导管结构是围绕轴线的轴对称结构，可以知道密封区域同一圆环的应力情况大致相同，且中间大两侧小。以球面切向的密封区域中点作为坐标零点，可以得到沿球面切向的接触应力分布图，如图8所示。接触应力关于密封区域中点不对成，最大接触应力略有偏移，但接触应力在密封区域中间部分变化平缓，直到密封区域边缘部分骤降。因此，密封结构主要依靠密封区域中间部分保证其密封性能，要保证在装配过程中的轴向对中，防止因中间区域轴向偏离而产生漏孔。

图7 密封区域接触应力Fig.7 Sealing Area Contact Stress

图8 拧紧力矩18.8N·m时密封区域接触应力分布Fig.8 Contact Stress Distribution in Sealing Area when Tightening Torque is 18.8N·m

4.4 结构材料强度校核

球面−锥面密封结构的导管连接件在施加力矩的过程中，球形接头、扩口式锥面接头及锁紧螺母的各部分都存在力的作用。在分析整体结构应力的时候会使用V.Mises理论[12]计算应力分布情况，这样能够在整个模型内部用应力等值线清楚表现应力分布，快速确定模型中超出屈服极限的最危险区域。导管在内压为2MPa作用下，拧紧力矩18.8N·m的密封条件下整个导管连接件的应力情况，如图9所示。

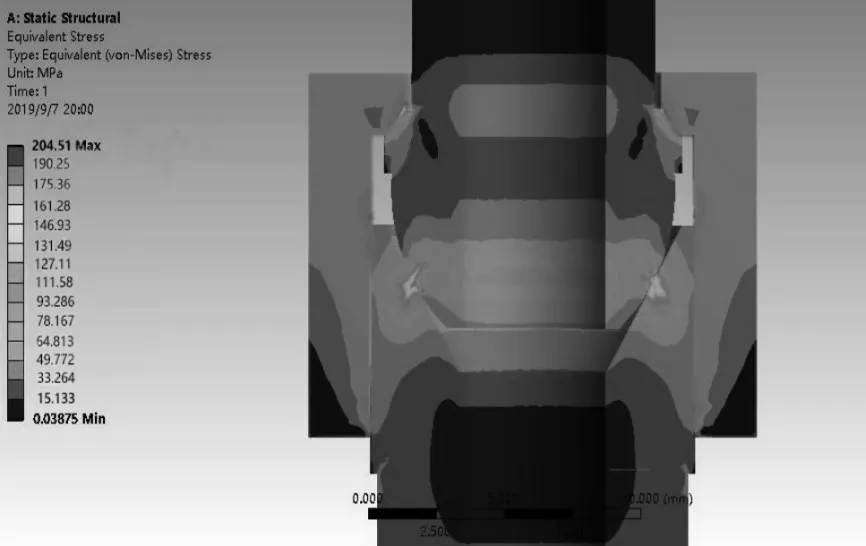
图9 拧紧力矩18.8N·m的导管连接件应力情况（内压2MPa）Fig.9 Stress Condition of the Pipe Joint with Tightening Torque of 18.8N·m（Internal Pressure 2MPa）

应力分布及密封面宽度基本不变，局部最大应力在球面与锥面的接触密封区域，但最大接触应力从208MPa 减小至204.5MPa，小于材料屈服极限，整体结构应力处于安全范围内。考虑内压增大到20MPa的情况下，整体结构应力计算结果略微增大，局部最大应力为216MPa，减小拧紧力矩至18N·m时能避免局部屈服的产生。因此，18.8N·m的拧紧力矩仍可作为导管安装扭矩上限值并保证密封性能，但内压明显增大的情况下要适当减小拧紧力矩。

5 实验验证

要验证理论分析所得数值具有准确性，需要经过实验得到密封面平均接触应力及密封面宽度与理论数值进行比较。考虑此处检测平均接触应力较为困难，故使用扫描电子显微镜扫描球头测量密封面宽度，根据Hertz接触理论可计算出密封面平均接触应力，因密封面宽度与密封面平均接触应力成一次正比关系，两者理论计算值与实际值误差相同。

为方便实验，设计制造了符合高压导管实际安装情况的实验装置，如图10所示。能实时反映拧紧力矩与轴向力大小。

图10 实验装置Fig.10 Experimental Device

为了合理验证分析结果，选取分析所得安装力矩上限值附近一定范围内12个力矩值作为拧紧力矩定值安装。

在实验中，采用FG−101型数显式力矩扳手，扳手具有力矩测量及预设力矩等功能，能够保证安装导管时施加力矩的精确且易于控制。

将导管接头至于实验装置上，用力矩扳手实现定力矩安装导管之后将接头拆开取下，采用JSM−6510扫描电子显微镜对球面接头表面进行扫描。如图11所示，通过100倍率放大扫描可以清晰直观地发现接头球面接触形成密封面的轮廓，得到密封面实际宽度。

图11 实验后接头球面扫描图Fig.11 Spherical Scan of the Joint After the Experiment

根据拧紧力矩值将实际密封面宽度Wy与理论密封面宽度W进行比较，如表1所示。

表1 密封面宽度理论计算值与实际值误差对比Tab.1 Comparison of Theoretical Calculation Value and Actual Value Error of Sealing Surface Width

经过理论计算值与实际值的对比，可以看出Wy与W的误差值控制在10%以内，这表明理论分析方法具有可行性，分析得到的数值具有准确性。

6 结论

（1）通过漏率经验公式并结合Hertz接触理论检漏，考虑内压大小对导管漏率影响预估导管初始密封状态具有可行性。

（2）导管装配过程中，拧紧力矩大小与密封面平均接触应力及密封面宽度成正比，相对较大的拧紧力矩能够加强球面−锥面密封结构的密封效果。

（3）对长期使用且具有较高密封要求的产品，需要定期检漏维护，减少应力松弛现象的产生。

（4）密封性能主要依靠密封面中间区域保证，要保证装配过程中的轴向对中，保持密封区域接触应力分布合理。

（5）合适的安装扭矩能够保证导管密封性能，不会对球面锥面密封结构造成局部屈服，能够满足定时检查导管密封状态重复拆装的使用要求。