一种双密封结构稳定漏率判定方法

龙 伟，赵肆方，杨才华，王隆基，李文静

（中国航天员科研训练中心，北京 100094）

0 引言

双密封结构大量应用于航天产品的密封结构中，双密封结构产品在进行氦质谱检漏时，不管是用氦质谱压力真空检漏，还是吸枪法单点检漏，常常出现示漏气体漏率缓慢爬升的现象，两道密封处的初始漏率越小，稳定平衡时间越长。针对双密封结构漏率测试的时间以及稳定漏率的判定，目前没有明确统一的方法，导致检漏结果不一致，特别是在稳定漏率略超出允许漏率，导致产品拒收时，分歧尤为突出[1-2]。

本文提出一种稳定漏率判定方法，通过建立漏率的增长模型，合理确定检漏时间，可以在示漏气体漏率曲线未平衡稳定的情况下预判稳定漏率，提高检漏效率。

1 双密封结构泄漏规律

1.1 双密封结构泄漏模型及数值分析

双密封结构原理和泄漏示意图如图1、2所示。恒压输入的示漏介质（纯氦）首先经过第一道密封（密封1）进入到两密封间的容积Vc，然后再经过第二道密封（密封2）进入氦质谱检漏仪。容积Vc初始状态下存有压力为常压、体积为Vc的空气。

图1 双密封结构原理图Fig.1 Schematic diagram of double sealed structure

图2 双密封结构泄漏示意图Fig.2 Leakage diagram of double sealed structure

双密封结构在检漏时，漏率不稳定的原因主要包括：

（1）由于氦质谱检漏仪只对氦信号有反应，随着检漏时间的延长，容积Vc内的氦浓度逐渐升高，氦分压逐渐增大，示漏气体漏率因此逐渐增大；

（2）由于密封1和密封2两处的漏率不同，容积Vc内的压力会发生变化，从而引起密封1和密封2处的漏率发生变化。

因此，双密封结构的泄漏过程与两道密封之间的容积Vc、密封1和密封2的漏率、容积Vc内的压力等都有密切关系[3]。

以分子流为例，密封件漏孔漏率与压差成正比，忽略温度和漏孔两端分子量平均值对漏率的影响以及示漏气体的扩散时间，输入气源为恒定压力的高纯氦气。气路系统与电路系统类似，气容等效于电容，流阻等效于电阻，气压等效于电压，两者有类似的模型，遵循相似的规律。因此，利用电路等效气路的方法以及气路相关理论约束[4-6]，建立氦质谱压力真空检漏法检漏的气路模型，如图3所示。双密封结构系统参数如表1所列。

图3 氦质谱压力真空检漏法检漏的气路模型图Fig.3 Gas path model of helium mass spectrometer pressure vacuum leak detection

表1 双密封结构系统参数Tab.1 System parameters of double sealed structure

根据漏率和压力、流阻的关系及气体量守恒，对图3模型做如下分析（式（1）～（4））：

整理后，可得到双密封结构密封1漏率、密封2漏率、两密封间容积内压力、氦分压随时间变化的数学模型（式（5）～（8））：

求解式（5）～（8）组成的一阶常系数线性微分方程组，再根据式（2）即可求得示漏气体漏率随时间的变化关系。假设某产品的Vc约为7.5 mm3，利用氦质谱压力真空检漏法检漏时，pin=4.04×105Pa。利用四阶龙格—库塔法求解由式（5）～（8）组成的微分方程组，编制程序求得在Q1（密封1漏率）、Q2（密封2漏率）不同的初始值下的计算结果，如表2所列。

表2 不同初始漏率下的稳定时间、稳定压力及稳定漏率Tab.2 Stable time，stable pressure and stable leakage rate under different initial leakage rates

从表 2 可以看出，当Q1=1.0×10-6Pa·m3/s、Q2=1.0×10-6Pa·m3/s，漏率稳定时间为 90 min；Q1=1.0×10-7Pa·m3/s、Q2=1.0×10-7Pa·m3/s，漏率稳定时间为875 min；Q1=1.0×10-8Pa·m3/s、Q2=1.0×10-8Pa·m3/s，漏率稳定时间为8 725 min。可以看出，示漏气体漏率的稳定是个缓慢的过程，特别是在每道密封漏率都很小的情况下，这个过程时间更长。后文1.2节试验测试数据和数值分析结论一致。利用吸枪法单点检漏时，也观察到类似的现象[5-6]，这进一步证明建立的数学模型的正确性。

1.2 双密封结构漏率测试分析

利用氦质谱压力真空检漏法，测试了三个双密封结构产品的漏率，测得稳定漏率分别为1.0×10-6Pa·m3/s、1.3×10-7Pa·m3/s和 5.4×10-8Pa·m3/s，其示漏气体漏率曲线分别如图4～6所示。可以看出，稳定漏率越小，稳定时间越长。当稳定漏率为1.0×10-6Pa·m3/s的双密封结构产品检漏时，漏率稳定时间约90 min；当稳定漏率为 1.3×10-7Pa·m3/s时，漏率稳定时间约1 810 min；当稳定漏率为5.4×10-8Pa·m3/s时，漏率稳定时间约2 700 min。

图4 稳定漏率值为1.0×10-6Pa·m3/s的示漏气体漏率曲线Fig.4 Leakage rate of indicator gas（stable leakage rate value：1.0×10-6Pa·m3/s）

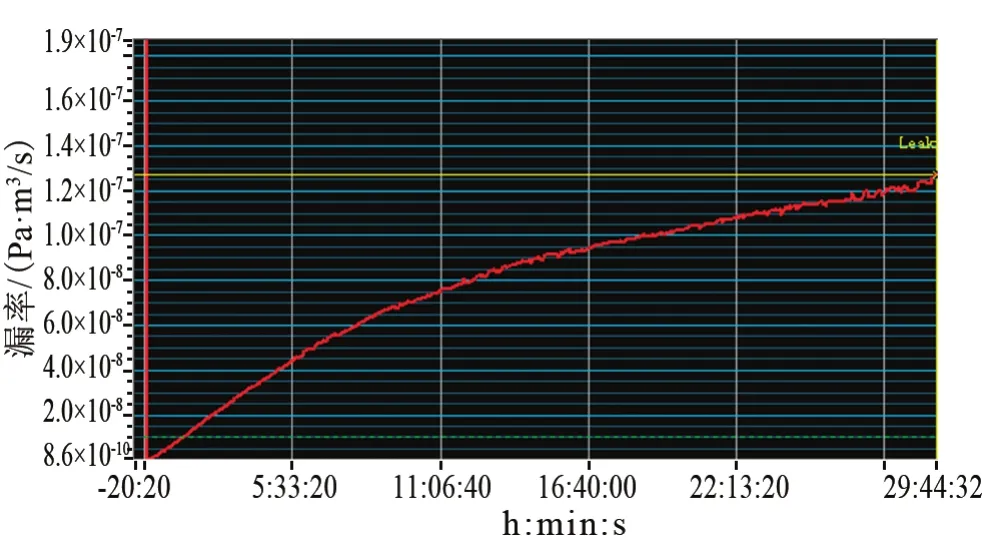
图5 稳定漏率值为1.3×10-7Pa·m3/s的示漏气体漏率曲线Fig.5 Leakage rate of indicator gas（stable leakage rate value：1.3×10-7Pa·m3/s）

图6 稳定漏率值为5.4×10-8Pa·m3/s的示漏气体漏率曲线Fig.6 Leakage rate of indicator gas（stable leakage rate value：5.4×10-8Pa·m3/s）

2 稳定漏率快速判定

2.1 稳定漏率快速判定方法

通过建立的双密封结构数学模型可知，示漏气体漏率随时间变化关系的数学表达式是一阶常系数线性微分方程。根据一阶常系数线性微分方程的通解公式可知其解为自然常数为底的指数函数类型。根据产品漏率测试曲线，发现双密封结构的漏率随时间呈指数增长，并且在初始时刻，示漏气体漏率近似为0，在测试曲线末端，示漏气体漏率趋于稳定。因此，采用Q（t）=a+be-t/c（a，b，c为常数）的指数函数式，建立示漏气体漏率随时间变化的近似数学关系。利用python软件编程对不同时间段的实测漏率值按所选定的指数函数进行曲线拟合[7-8]，得到a，b，c等3个拟合常数。

不断增加测试时长，可得到一系列a1，a2，a3，…，an值（即稳定漏率预测值），当相邻两次测试a值的拟合误差（拟合误差=[（an+1-an）/an+1]×100%）不大于给定的控制值时，即可认为an+1值就是漏率的稳定测量值。当t→∞，a与漏率真值间的误差趋于0。按照该方法，就可以大幅缩短获得在允许误差范围内稳定漏率的时间，提高测试效率。

由于检漏初始的几分钟，因受检漏系统本底、被检件初始状态等因素影响，不选取采样点。

2.2 实例应用与分析

利用2.1节所述方法分别对图4～6的漏率曲线进行分析拟合，曲线拟合结果分别如图7～9所示。稳定漏率预测值与试验值对比如表3～5所列，表中拟合误差（（an+1-an）/an+1×100%）为相邻两个取样间隔拟合值的相对变化量，相对误差（[（稳定漏率预测值-稳定漏率试验值）/稳定漏率试验值]×100%）为利用指数函数拟合的稳定漏率预测值与稳定漏率试验值间的相对偏差值。

表3 稳定漏率预测值和试验值对比（稳定漏率值：1.0×10-6Pa·m3/s）Tab.3 Comparison for predictive value of stable leakage and test stabilized leakage rates（stable leakage rate value：1.0×10-6Pa·m3/s）

针对稳定漏率为1.0×10-6Pa·m3/s的测试数据，数据点每隔5 min进行取值。不同时间段的拟合曲线如图7所示，稳定漏率预测值与试验值对比如表3所列。从图7和表3可以看出，随着测试时间的延长，拟合误差绝对值和相对误差整体趋势逐渐减小。当双密封结构产品的稳定漏率为1.0×10-6Pa·m3/s时，试验稳定时间约90 min，利用本文方法预测稳定漏率，当允许误差分别为20%、10%时，预测稳定漏率所用测试时间约为40 min、60 min，检漏效率能提高约55%、33%。

图7 稳定漏率为1.0×10-6Pa·m3/s的双密封结构不同周期的漏率拟合曲线Fig.7 Fitting curves of leakage rates for different periods of double sealed structures with stable leakage rate of 1.0×10-6Pa·m3/s

针对稳定漏率为1.3×10-7Pa·m3/s的测试数据，采用同样方法进行拟合。前600 min内采样间隔为20 min，600 min之后采样间隔为30 min。不同时间的拟合曲线如图8所示，稳定漏率预测值与试验值对比如表4所列。从图8和表4可以看出，随着测试时间的延长，拟合误差绝对值和相对误差整体趋势均逐渐减小。当双密封结构产品的稳定漏率为 1.3×10-7Pa·m3/s，试验稳定时间需要约1 810 min。利用本文方法预测稳定漏率，当允许误差分别为30%、20%、10%时，漏率测试时间分别为520 min、660 min、840 min，检漏效率能提高分别约71%、63%、53%。

图8 稳定漏率为1.3×10-7Pa·m3/s的双密封结构不同周期的漏率拟合曲线Fig.8 Fitting curves of leakage rates for different periods of double sealed structures with stable leakage rate of 1.3×10-7Pa·m3/s

表4 稳定漏率预测值和试验值对比（稳定漏率值：1.3×10-7Pa·m3/s）Tab.4 Comparison for predictive value of stable leakage and test stabilized leakage rates（stable leakage rate value：1.3×10-7Pa·m3/s）

针对稳定漏率为5.4×10-8Pa·m3/s的数据，采用同样方法进行拟合。前600 min内采样间隔为20 min，600 min之后采样间隔为30 min。不同周期的拟合曲线如图9所示，稳定漏率预测值与试验值对比如表5所列。

表5 稳定漏率预测值和试验值对比（稳定漏率值：5.4×10-8Pa·m3/s）Tab.5 Comparison for predictive value of stable leakage and test stabilized leakage rates（stable leakage rate value：5.4×10-8Pa·m3/s）

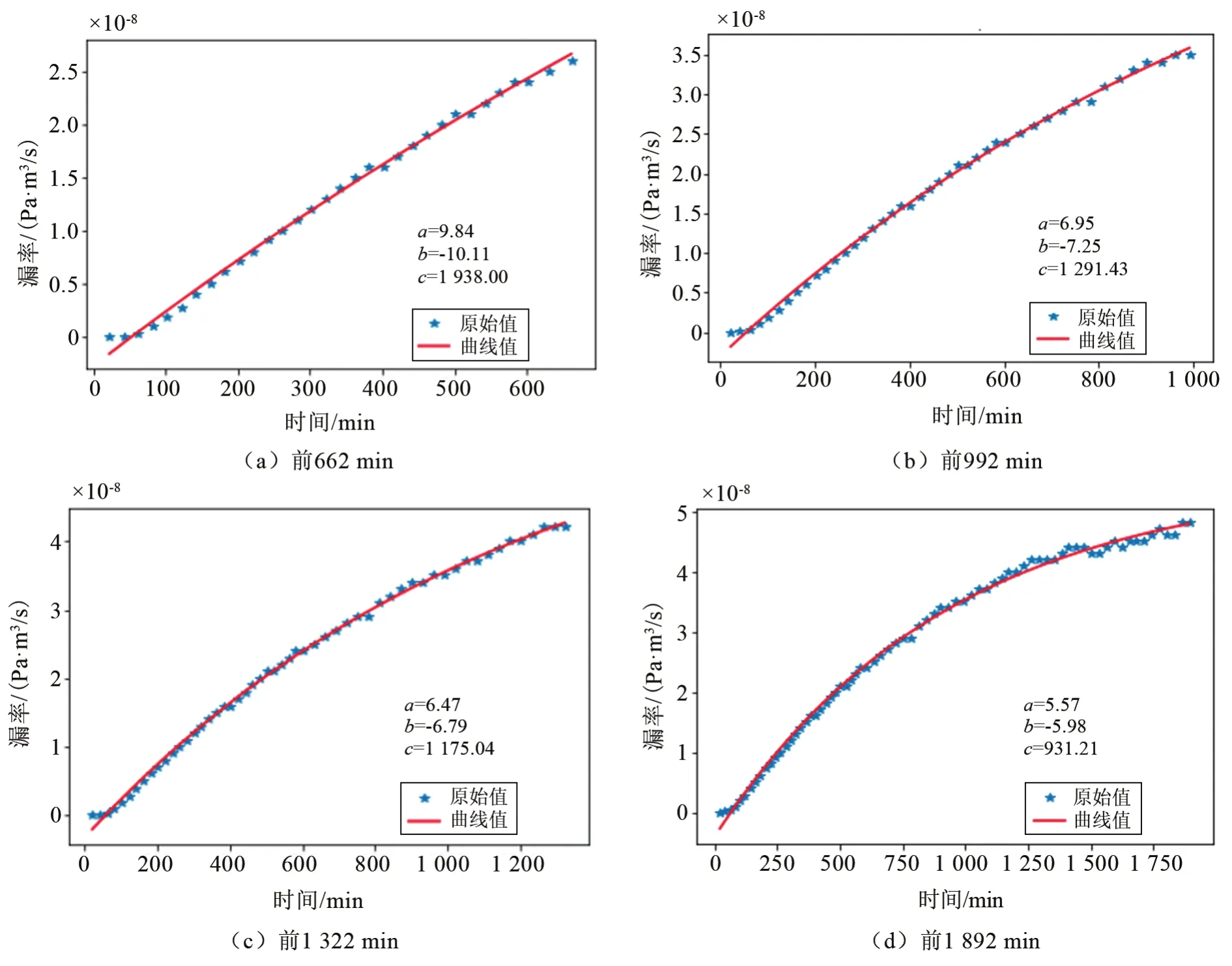
图9 稳定漏率为5.4×10-8Pa·m3/s的双密封结构不同周期的漏率拟合曲线Fig.9 Fitting curves of leakage rates for different periods of double sealed structures with stable leakage rate of 5.4×10-8Pa·m3/s

从图9和表5可以看出，与前两个实例类似，随着测试时间的延长，拟合误差绝对值和相对误差整体趋势亦逐渐减小。当双密封结构产品的稳定漏率为5.4×10-8Pa·m3/s，试验稳定时间需要约 2 700 min，利用该方法预测稳定漏率，当允许误差分别为30%、20%、10%时，预测稳定漏率所用测试时间约为992 min、1 322 min、1 592 min，检漏效率能提高约63%、51%、41%。

2.3 应用判定方法的几点建议

本文中的双密封结构，在压力真空法检漏时，其稳定漏率一般都在1.0×10-6～1.0×10-8Pa·m3/s区间内。在实际应用中，本判定方法的应用与检漏时间的确定按如下建议进行：

（1）对某种产品第一件检漏时，检漏时间为直到示漏气体漏率曲线漏率显示稳定时为止，获取完整的示漏气体漏率曲线和试验数据；

（2）如文中实例一样，对第一件产品的示漏气体漏率曲线，在不同检漏时间段内采样后分别进行函数拟合，得到不同检漏时间的稳定漏率预测值，并计算相对误差；

（3）该种产品其余件检漏，应用第一件产品示漏气体漏率曲线的拟合分析结果，根据可接受的相对误差来确定该件产品的检漏时间，然后在该检漏时间内对示漏气体漏率曲线采样，按照本文方法进行函数拟合，得到预测稳定漏率值即为本次检漏的稳定漏率值；

（4）若出现同种产品示漏气体漏率曲线偏离较大时，检漏时间就以示漏气体漏率曲线漏率显示稳定时为止。

3 结语

对双密封结构产品进行氦质谱压力真空法检漏时，应用文中指定函数类型进行曲线拟合的方法来预测稳定漏率，能缩短示漏气体稳定漏率的判定时间，极大提高检漏效率，特别是对于10-7Pa·m3/s、10-8Pa·m3/s量级的微漏产品。实际应用中，可根据经验证实的应用实例及可接受的相对误差来确定检漏时间，既保证漏率测试的准确性，又能提高检漏效率，对双密封结构产品检漏工作具有一定的指导意义。后续工作有待进一步探索更加合适的拟合函数，在更短的测试时间内减小稳定漏率预测相对误差，进一步提升检漏效率。