返回舱再入过程密封舱气体泄漏计算研究
黄震,赵建贺,李志杰
返回舱再入过程密封舱气体泄漏计算研究
黄震,赵建贺,李志杰
(中国空间技术研究院载人航天总体部,北京 100094)
为分析返回舱再入过程中密封舱漏孔内外压差,并对漏孔变流量充气过程进行研究,采用离散化分析方法将返回舱再入过程分成若干个阶段,针对容积为14 m3的密封舱和面积为10cm2的漏孔,计算并获得了密封舱内外压差、漏孔质量流率、漏孔流速等参数在50~5km范围内随高度下降的变化规律。结果表明:在高度5km开伞时刻,漏孔质量流率达到最大值0.134 kg/s,舱内外压差趋近于最大值,约20172Pa;返回舱下降过程中漏孔流速在148.4~181.5 m/s之间,处于亚声速区;漏孔气体流速与漏孔面积大小无关,仅与漏孔内外压力及漏孔进口空气密度有关。以上研究结果可为密封舱结构强度设计、伞舱弹伞设计提供参考。
密封舱;再入;漏孔;压力差;质量流率;气体流速;计算分析
0 引言
飞船长期在轨飞行,返回舱可能被微流星体或空间碎片击中而产生漏孔[1-6],这种情况下密封舱内气体会逐渐泄漏至外太空,致使舱内变成真空状态。当返回舱再入时,随高度下降,密封舱外压力逐渐增大,外界空气通过小孔向舱内变流量充气,致使舱内气体压力逐渐升高,最终导致返回舱内外压差持续变化。
密封舱在进行结构强度设计时,主要考虑在轨承受0.1MPa的内压。而当密封舱产生漏孔时,返回舱在轨泄漏成真空,其再入过程中则需反向承受最大0.1MPa的外压,这个外压可能造成返回舱被压而局部发生形变。
密封舱泄漏虽然属小概率事件,但对其泄漏规律研究意义重大。假若由于碎片撞击或舱体密封故障导致舱体产生漏孔,舱体内外压力差及漏孔流速会对返回舱的安全及飞行产生重大影响。除了返回舱在返回过程中需要承受外界对舱体最大0.1MPa的压力外,空气泄漏的反推作用力可能会对舱体飞行姿态产生影响,轻则导致较大落点偏差,重则导致返回舱姿态翻转无法正常返回。另外,如果伞舱与密封舱联通,由于密封舱内外较大的负压力差可能使得伞舱盖无法弹开,导致开伞失败,后果不堪设想。
因此,需要对密封舱漏孔泄漏这一工程问题进行细致研究,从而获得密封舱内外压差、漏孔流速、漏孔质量流率等变化规律,研究结果可为密封舱设计提供参考。
1 漏孔泄漏质量流率
1)当漏孔的空气流速处于亚声速范围时[7-9],有

式中:=o/i值,o和i分别为漏孔出口气压和进口气压;为空气定压比热容与定容比热容之比,其取值范围参见文献[10-11]。
通过漏孔的空气质量流率为
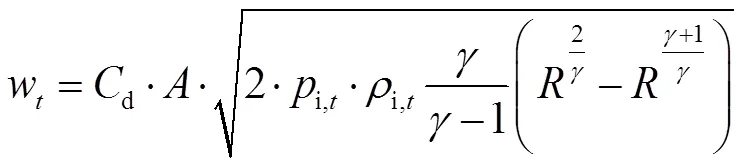
2)当漏孔的空气流速处于声速范围[7-9],有

通过漏孔的空气质量流率为
。 (4)
3)当漏孔的空气质量流率处于分子流范围时,通过漏孔的空气质量流率为[7-9]
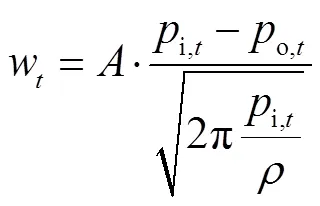
2 案例分析
2.1 分析模型
为简化漏孔空气泄漏分析,假设如下:
1)空气为理想气体,漏孔处的气流无摩擦且连续,且不与密封舱发生热交换;
2)泄漏气体速度方向垂直于漏孔所属表面。
图1为返回舱返回再入过程中,其所处的高度与时间(以距海平面50km高度处作为0时刻)的对应关系。载人航天器一般运行在300~400 km高的低地球轨道,文献[12]显示50km高度处大气压力为79.8Pa。50km以上的大气太过稀薄,因此仅分析50km及以下高度处的空气泄漏情况即可再现返回舱再入过程中的泄漏过程。由于返回舱下降至5km高度处开伞,所以本文仅分析50~5km高度这一飞行过程中漏孔质量流率、压差及速度等参数的变化情况。
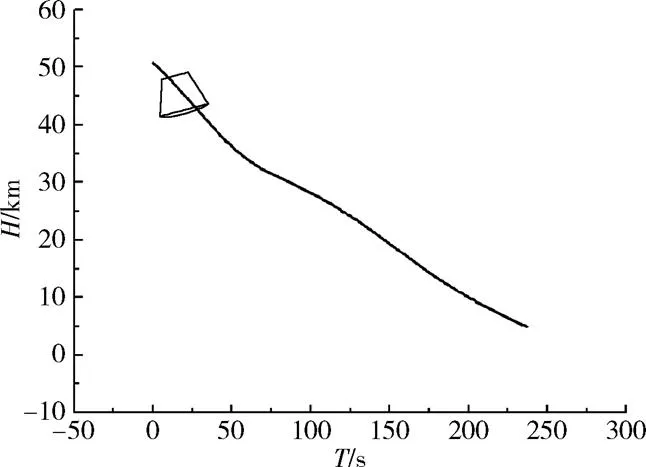
图1 返回舱所处高度与时间的对应情况
从图1可知时刻返回舱所处的高度及Δ时间内返回舱下降的高度,从而获得时刻返回舱所处位置的大气参数(包括压力、密度),以及Δ时间段内密封舱漏孔进口质量流率,再通过积分运算得到Δ时间段内泄漏入密封舱内的空气质量:

根据密封舱内气体质量,获得返回舱内实时气压,从而计算出不同高度处返回舱内外压差。
2.2 漏孔质量流率变化情况
本研究的返回舱之密封舱的容积为14m3,漏孔面积为10cm2,假设泄漏空气流速为亚声速,由式(2)获得漏孔质量流率随返回舱高度下降的变化趋势,如图2所示。从图2中可以看出,当返回舱从50km高度下降至20km的过程中,舱内进气速率较为平缓;20km高度之后,漏孔质量流率增加较快;返回舱高度下降至5km高度开伞时,漏孔质量流率达到最大值0.134kg/s。
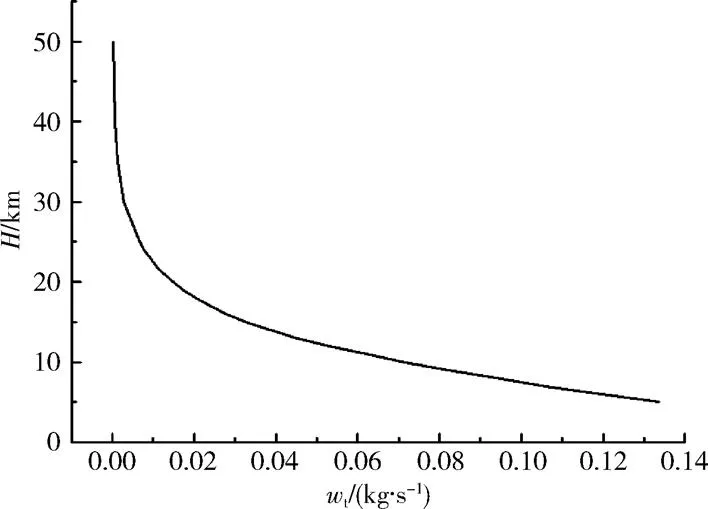
图2 漏孔质量流率随高度下降的变化
2.3 漏孔内外压力、压差变化情况
对返回舱再入飞行时密封舱的充气过程进行离散化迭代计算,返回舱漏孔内外压力及内外压差随返回舱高度下降变化趋势分别如图3和图4所示。

图3 返回舱内外压力随高度下降的变化

图4 漏孔内外压差随高度下降的变化
从图4可以看出,返回舱从50km高度下降的过程中,舱体内外压差呈现出逐渐增大的趋势,在高度达到5km返回舱开伞时刻,返回舱内外压差趋近于最大值,约20172Pa。
2.4 密封舱漏孔流速
根据质量流率=密度×(流速×漏孔面积),漏孔质量流率又可表述为w=i··。漏孔的泄漏空气流速为亚声速,结合式(2),有

得到漏孔流速为
。 (8)
由式(8)可知,漏孔流速与漏孔面积无关,仅与漏孔内外压力及漏孔进口空气密度有关。进一步计算得出返回舱下降过程中漏孔流速在148.4~181.5m/s之间,处于亚声速区。
2.5 不同漏孔面积下密封舱内外压差情况
图5给出了距地面5km高度处,密封舱内外压力差随漏孔面积的变化情况。
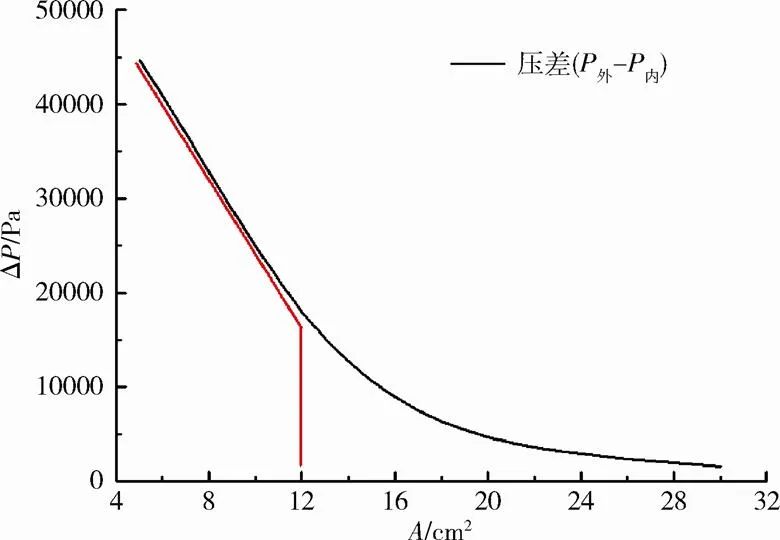
图5 返回舱内外压差随漏孔面积变化情况(5 km高度)
从图5中可以看出,当漏孔面积大于30cm2时,返回舱内外压差在1500Pa以下;当漏孔面积小于12cm2时,返回舱内外压差急剧增大。
3 结束语
本文给出了某返回舱再入过程中密封舱泄漏时相关参数的计算思路与计算结果。通过对密封舱充气过程作离散化迭代分析,可获得漏孔变化的质量流率、密封舱内外压力与压差分布、密封舱漏孔流速等参数,分析结果可为返回舱结构强度设计、伞舱弹伞设计等提供重要参考。通过分析,获得结论如下:
1)返回舱再入大气过程中,密封舱漏孔质量流率和漏孔内外压差均随高度下降而增大;
2)漏孔气体流速与漏孔面积大小无关,仅与漏孔内外压力及漏孔进口空气密度有关,对于亚声速泄漏,漏孔流速表达式见式(9)。同理可获得声速及分子流条件下的漏孔流速。
此外,本文中的计算方法可以进行拓展应用,如估算火箭发射上升过程中的整流罩内外压差。
[1] 李久龙, 吴光中, 姜联东. 空间碎片对航天器的撞击效果分析[J]. 航天器环境工程, 2009, 26(增刊1): 9-13
LI J L, WU G Z, JIANG L D. Research on effectfor satellite impacted by space debris[J]. Spacecraft Environment Engineering, 2009, 26(sup1): 9-13
[2] 龚自正, 徐坤博, 牟永强, 等. 空间碎片环境现状与主动移除技术[J]. 航天器环境工程, 2014, 31(2): 129-135
GONG Z Z, XU K B, MU Y Q, et al. The space debris environment and the active debris removal techniques[J]. Spacecraft Environment Engineering, 2014, 31(2): 129-135
[3] 王晓宇, 张超, 孙维, 等. 航天器密封舱加筋壁板碎片撞击监测技术研究[J]. 实验流体力学, 2014, 28(4): 70-77
WANG X Y, ZHANG C, SUN W, et al. Research on structural health monitoring method for locating space debris impact on spacecraft seal structures[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(4): 70-77
[4] 周智炫, 黄洁, 任磊生, 等. 卫星在空间碎片撞击下的易损性分析方法研究[J]. 实验流体力学, 2014, 28(3): 87-92
ZHOU Z X, HUANG J, REN L S, et al. Research on vulnerability analysis method for satellite impacted by space debris[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(3): 87-92
[5] 张永, 李明, 韩增尧. 微流星体/空间碎片环境下压力舱的气体泄漏分析[J]. 航天器环境工程, 2008, 25(4): 310-314
ZHANG Y, LI M, HAN Z Y. Analysis for leakage of sealed cabin against meteoroid and orbital debris[J]. Spacecraft Environment Engineering, 2008, 25(4): 310-314
[6] 李凌江, 刘武刚, 王建民, 等. 多孔铝板高速撞击声发射定位方法[J]. 航天器环境工程, 2016, 33(6): 589-593
LI L J, LIU W G, WANG J M, et al. Acoustic emission localization of hypervelocity impact in perforated plate[J]. Spacecraft Environment Engineering, 2016, 33(6): 589-593
[7] EcosimPro ECLSS Library Reference Manual: Professional dynamic modeling and simulation tool for industrial applications[G]. Version 3.0. EA International, 2008: 317-319
[8] 靳健. 载人航天器密封舱泄漏时舱压控制分析[J]. 载人航天, 2017, 23(1): 21-27
JIN J. Analysis of air pressure control in pressurized cabin of manned spacecraft during cabin leaking[J]. Manned Spaceflight, 2017, 23(1): 21-27
[9] 靳健, 杨晨, 侯永青. 一种载人航天器气压控制系统仿真模型[J]. 航天器工程, 2015, 24(3): 51-57
JIN J, YANG C, HOU Y Q. Simulaton model for air pressure control system of manned spacecraft[J]. Spacecraft Engineering, 2015, 24(3): 51-57
[10] MORAN M J, SHPIRO H N. Fundamentals of engineering thermodynamics[M]. 3rd ed. New York: John Wiley & Sons Inc, 1995
[11] 沈维道, 蒋智敏, 童钧耕. 工程热力学[M]. 3版. 北京: 高等教育出版社, 2001: 393-412
[12] National Aeronautics and Space Administration. U.S. Standard Atmosphere: NASA-TM-X-74335[R]. Washington DC: U.S. Government Printing Office, 1976
(编辑:闫德葵)
Leakage of a sealed cabin in re-entry flight
HUANG Zhen, ZHAO Jianhe, LI Zhijie
(Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China)
The pressure difference of inside and outside the orifice of a sealed cabin in the re-entry flight is studied, and the variable gas charging process of the orifice is analyzed. A discretized analytical method is used for the calculation of a sealed cabin with a volume of 14 m3and an orifice with an area of 10 cm2. The pressure difference of the sealed cabin, the mass flow rate, and the gas velocity in the orifice against the time or height are obtained. The results show that at the height of 5 km, the mass flow rate reaches its highest value of 0.134 kg/s; the pressure difference approaches the maximum; the gas velocity ranges between 148.4~181.5 m/s(in the subsonic zone); and the gas velocity in the orifice is related only with the inlet and outlet pressure of the orifice and the inlet gas density, while regardless of the area of the orifice. The above results may provide a reference for the design of capsule structures and parachute-module systems.
sealed cabin; re-entry; leak hole; pressure difference; mass flow rate; gas velocity; calculation analysis
V520; V423.5
A
1673-1379(2017)04-0415-04
10.3969/j.issn.1673-1379.2017.04.013
黄震(1982—),男,博士学位,研究员,主要从事载人航天器总体设计工作;E-mail: huangzhencast@126.com。通信作者:赵建贺(1985—),男,博士学位,高级工程师,主要从事载人航天器总体设计工作;E-mail: zhaojianhe@live.cn。
2016-10-13;
2017-07-20
国家重大科技专项工程

